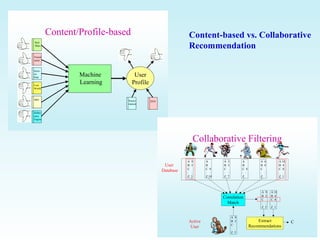
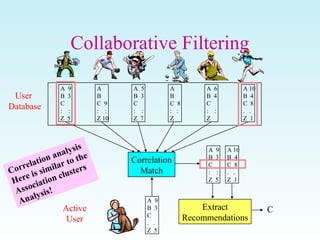
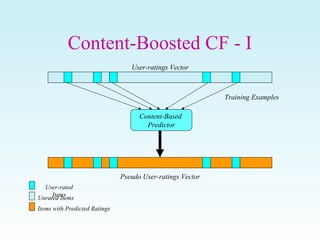
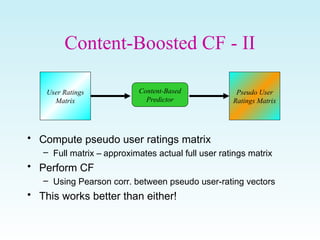
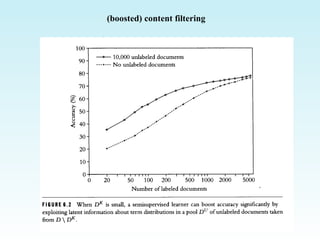
This document discusses various techniques for filtering and recommender systems, including content-based filtering, collaborative filtering, and hybrid approaches. It provides an overview of key concepts such as using user profiles and feedback to provide personalized recommendations. It also covers common recommendation algorithms like nearest neighbor collaborative filtering and discusses challenges like cold start problems and sparsity issues.

1. Filtering and
Recommender
Systems
Content-based
and
Collaborative
Some of the slides based
On Mooney’s Slides

2. Personalization
• Recommenders are instances of
personalization software.
• Personalization concerns adapting to the
individual needs, interests, and preferences of
each user.
• Includes:
– Recommending
– Filtering
– Predicting (e.g. form or calendar appt. completion)
• From a business perspective, it is viewed as
part of Customer Relationship Management
(CRM).

3. Feedback &
Prediction/Recommendation
• Traditional IR has a single user—probably
working in single-shot modes
– Relevance feedback…
• WEB search engines have:
– Working continually
• User profiling
– Profile is a “model” of the user
• (and also Relevance feedback)
– Many users
• Collaborative filtering
– Propagate user preferences to other
users…
You know this one

4. Recommender Systems in Use
• Systems for recommending items (e.g. books,
movies, CD’s, web pages, newsgroup
messages) to users based on examples of
their preferences.
• Many on-line stores provide
recommendations (e.g. Amazon, CDNow).
• Recommenders have been shown to
substantially increase sales at on-line stores.

5. Feedback Detection
– Click certain pages in
certain order while ignore
most pages.
– Read some clicked pages
longer than some other
clicked pages.
– Save/print certain clicked
pages.
– Follow some links in
clicked pages to reach
more pages.
– Buy items/Put them in
wish-lists/Shopping Carts
– Explicitly ask users to
rate items/pages
Non-Intrusive Intrusive

6. Justifying Recommendation..
• Recommendation systems must justify their
recommendations
– Even if the justification is bogus..
– For search engines, the “justifications” are the page
synopses
• Some recommendation algorithms are better at
providing human-understandable justifications than
others
– Content-based ones can justify in terms of classifier
features..
– Collaborative ones are harder-pressed other than saying
“people like you seem to like this stuff”
– In general, giving good justifications is important..

7. Content/Profile-based
Red
Mars
Juras-
sic
Park
Lost
World
2001
Found
ation
Differ-
ence
Engine
Machine
Learning
User
Profile
Neuro-
mancer
2010
Collaborative Filtering
A 9
B 3
C
: :
Z 5
A
B
C 9
: :
Z 10
A 5
B 3
C
: :
Z 7
A
B
C 8
: :
Z
A 6
B 4
C
: :
Z
A 10
B 4
C 8
. .
Z 1
User
Database
Active
User
Correlation
Match
A 9
B 3
C
. .
Z 5
A 9
B 3
C
: :
Z 5
A 10
B 4
C 8
. .
Z 1
Extract
Recommendations
C
Content-based vs. Collaborative
Recommendation

8. Collaborative Filtering
A 9
B 3
C
: :
Z 5
A
B
C 9
: :
Z 10
A 5
B 3
C
: :
Z 7
A
B
C 8
: :
Z
A 6
B 4
C
: :
Z
A 10
B 4
C 8
. .
Z 1
User
Database
Active
User
Correlation
Match
A 9
B 3
C
. .
Z 5
A 9
B 3
C
: :
Z 5
A 10
B 4
C 8
. .
Z 1
Extract
Recommendations
C
Correlation analysis
Here is similar to the
Association clusters
Analysis!

9. Item-User Matrix
• The input to the collaborative filtering
algorithm is an mxn matrix where rows are
items and columns are users
– Sort of like term-document matrix (items are terms
and documents are users)
• Can think of users as vectors in the space of
items (or vice versa)
– Can do vector similarity between users
• And find who are most similar users..
– Can do scalar clusters over items etc..
• And find what are most correlated items
Thinkusers

docs
Items

keywords

10. A Collaborative Filtering Method
(think kNN regression)
• Weight all users with respect to similarity with the
active user.
– How to measure similarity?
• Could use cosine similarity; normally pearson coefficient is used
• Select a subset of the users (neighbors) to use as
predictors.
• Normalize ratings and compute a prediction from a
weighted combination of the selected neighbors’
ratings.
• Present items with highest predicted ratings as
recommendations.

11. 3/27
Homework 2 Solns posted
Midterm on Thursday in class
Covers everything covered by the first two
homeworks
Qns??
Today
Complete Filtering
Discuss Das/Datar paper

12. Finding User Similarity with Person
Correlation Coefficient
• Typically use Pearson correlation coefficient
between ratings for active user, a, and another
user, u.
ua rr
ua
ua
rr
c
σσ
),(covar
, =
ra and ru are the ratings vectors for the m items rated by
both a and u
ri,j is user i’s rating for item j
m
rrrr
rr
m
i
uiuaia
ua
∑=
−−
= 1
,, ))((
),(covar
m
rr
m
i
xix
rx
∑=
−
= 1
2
, )(
σ
m
r
r
m
i
ix
x
∑=
= 1
,

13. Neighbor Selection
• For a given active user, a, select correlated
users to serve as source of predictions.
• Standard approach is to use the most similar
k users, u, based on similarity weights, wa,u
• Alternate approach is to include all users
whose similarity weight is above a given
threshold.

14. Rating Prediction
• Predict a rating, pa,i, for each item i, for active user,
a, by using the k selected neighbor users,
u ∈ {1,2,…k}.
• To account for users different ratings levels, base
predictions on differences from a user’s average
rating.
• Weight users’ ratings contribution by their similarity
to the active user.
∑
∑
=
=
−
+= n
u
ua
n
u
uiuua
aia
w
rrw
rp
1
,
1
,,
,
||
)(
ri,j is user i’s rating for item j
ua rr
ua
ua
rr
c
σσ
),(covar
, =

15. Similarity Weighting=User
Similarity
• Typically use Pearson correlation coefficient
between ratings for active user, a, and another
user, u.
ua rr
ua
ua
rr
c
σσ
),(covar
, =
ra and ru are the ratings vectors for the m items rated by
both a and u
ri,j is user i’s rating for item j
m
rrrr
rr
m
i
uiuaia
ua
∑=
−−
= 1
,, ))((
),(covar
m
rr
m
i
xix
rx
∑=
−
= 1
2
, )(
σ
m
r
r
m
i
ix
x
∑=
= 1
,

16. Significance Weighting
• Important not to trust correlations based
on very few co-rated items.
• Include significance weights, sa,u, based
on number of co-rated items, m.
uauaua csw ,,, =








≤
>
=
50if
50
50if1
, m
m
m
s ua
ua rr
ua
ua
rr
c
σσ
),(covar
, =

17. Problems with Collaborative Filtering
• Cold Start: There needs to be enough other users
already in the system to find a match.
• Sparsity: If there are many items to be recommended,
even if there are many users, the user/ratings matrix is
sparse, and it is hard to find users that have rated the
same items.
• First Rater: Cannot recommend an item that has not
been previously rated.
– New items
– Esoteric items
• Popularity Bias: Cannot recommend items to
someone with unique tastes.
– Tends to recommend popular items.
• WHAT DO YOU MEAN YOU DON’T CARE FOR BRITNEY
SPEARS YOU DUNDERHEAD? #$%$%$&^

18. Content-Based Recommending
• Recommendations are based on
information on the content of items
rather than on other users’ opinions.
• Uses machine learning algorithms to
induce a profile of the users
preferences from examples based on a
featural description of content.
• Lots of systems

19. Adapting Naïve Bayes idea for Book
Recommendation
• Vector of Bags model
– E.g. Books have several
different fields that are all
text
• Authors, description, …
• A word appearing in one
field is different from the
same word appearing in
another
– Want to keep each bag
different—vector of m Bags;
Conditional probabilities for
each word w.r.t each class
and bag
• Can give a profile of a
user in terms of words
that are most predictive
of what they like
– Odds Ratio
P(rel|example)/P(~rel|
example)
An example is positive if the
odds ratio is > 1
– Strengh of a keyword
• Log[P(w|rel)/P(w|~rel)]
– We can summarize a
user’s profile in terms of
the words that have
strength above some
threshold.
∏∏= =
=
S
m
dm
i
mi smcjaP
BookP
cjP
BookcjP
1
||
1
),|(
)(
)(
)|(

20. Advantages of Content-Based
Approach
• No need for data on other users.
– No cold-start or sparsity problems.
• Able to recommend to users with unique tastes.
• Able to recommend new and unpopular items
– No first-rater problem.
• Can provide explanations of recommended items
by listing content-features that caused an item to
be recommended.
• Well-known technology The entire field of
Classification Learning is at (y)our disposal!

21. Disadvantages of Content-Based
Method
• Requires content that can be encoded as
meaningful features.
• Users’ tastes must be represented as a
learnable function of these content features.
• Unable to exploit quality judgments of other
users.
– Unless these are somehow included in the content
features.

22. Content-Boosted CF - I
Content-Based
Predictor
Training Examples
Pseudo User-ratings Vector
Items with Predicted Ratings
User-ratings Vector
User-rated
Items
Unrated Items

23. Content-Boosted CF - II
• Compute pseudo user ratings matrix
– Full matrix – approximates actual full user ratings matrix
• Perform CF
– Using Pearson corr. between pseudo user-rating vectors
• This works better than either!
User Ratings
Matrix
Pseudo User
Ratings Matrix
Content-Based
Predictor

24. Why can’t the pseudo ratings be
used to help content-based filtering?
• How about using the pseudo ratings to improve a content-based filter
itself? (or how access to unlabelled examples improves accuracy…)
– Learn a NBC classifier C0 using the few items for which we have user ratings
– Use C0 to predict the ratings for the rest of the items
– Loop
• Learn a new classifier C1 using all the ratings (real and predicted)
• Use C1 to (re)-predict the ratings for all the unknown items
– Until no change in ratings
• With a small change, this actually works in finding a better classifier!
– Change: Keep the class posterior prediction (rather than just the max class)
• This means that each (unlabelled) entity could belong to multiple classes—with
fractional membership in each
• We weight the counts by the membership fractions
– E.g. P(A=v|c) = Sum of class weights of all examples in c that have A=v divided by Sum
of class weights of all examples in c
• This is called expectation maximization
– Very useful on web where you have tons of data, but very little of it is
labelled
– Reminds you of K-means, doesn’t it?

26. (boosted) content filtering

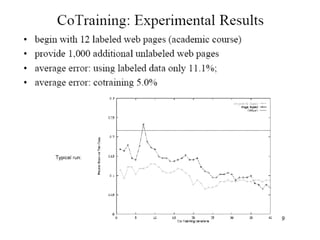
27. Co-training
• Suppose each instance has two parts:
x = [x1, x2]
x1, x2 conditionally independent given f(x)
• Suppose each half can be used to classify instance
∃f1, f2 such that f1(x1) = f2(x2) = f(x)
• Suppose f1, f2 are learnable
f1 ∈ H1, f2 ∈ H2, ∃ learning algorithms A1, A2
Unlabeled Instances
[x1, x2]
Labeled Instances
<[x1, x2], f1(x1)>A1 f2
Hypothesis
~
A2
Small labeled data needed
You train me—I train you…

28. Observations
• Can apply A1 to generate as much training
data as one wants
– If x1 is conditionally independent of x2 / f(x),
– then the error in the labels produced by A1
– will look like random noise to A2 !!!
• Thus no limit to quality of the hypothesis
A2 can make

30. Discussion of the Google News
Collaborative Filtering Paper