This presentation introduces the RSA encryption algorithm. It explains that RSA uses a public/private key pair to encrypt and decrypt messages. The steps are: 1) Generate prime numbers p and q to calculate the modulus n=pq. 2) Determine the public exponent e that is relatively prime to φ(n). 3) Calculate the private exponent d, which satisfies ed=1 mod φ(n). 4) The public key is the modulus n and public exponent e, while the private key is n and private exponent d. Encryption uses the public key to calculate ciphertext C=Me mod n from plaintext M. Decryption with the private key calculates M=Cd mod n to recover the original plaintext.

1. Welcome to my Presentation
on
RSA Algorithm
MD.KAWSAR AHMED
DEPARTMENT OF ICE, PABNA UNIVERSITY OF SCIENCE AND TECHNOLOGY

2. What is RSA algorithm?
 It is a public key encryption technique and is the most secure way of
Encryption.
The word ‘RSA’ is coming from three names:
R=Rivest
S=Shamir
A= Adelman
Rivest, Shamir and Adelman proposed this algorithm in 1978. According to
their name, the Algorithm name’s “RSA”.

3. Basic equation for Encryption and
Decryption
Plaintext Block, M = Cd mode n
Cipher text Block, C = Me mode n

4. Algorithm of RSA

5. Step 01: Generate the RSA modulus
 The initial procedure begins with the selection of to prime numbers p and
q then we have to find the value of ‘n’.
 Here n = p * q;

6. Step 02: Generate Derived Number ‘e’
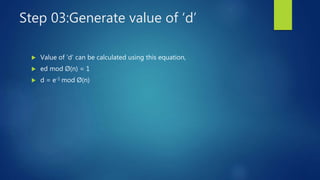
Derived number e and d can be calculated by using this equation. it is known
that,
ed mod Ø(n) = 1
[ here, Ø(n) = (p-1) * (q-1)] and Ø(n) is called Euler totient Function.
‘e’ can calculated such a way where gcd{Ø(n),e} = 1
And will be calculated by

7. Step 03:Generate value of ‘d’
 Value of ‘d’ can be calculated using this equation,
 ed mod Ø(n) = 1
 d = e-1 mod Ø(n)

8. Step 04: Public and private Key
Generation
 Public key ,pu = {n,e}
 Private key, pb = {n,d}

9. Algorithm summary
 Take two prime number p and q
 n = p*q
 Find value e, with gcd{Ø(n),e} = 1
 Find d = e-1 mod Ø(n)
 Public key, pu ={n,e}
 Publlic key, ={n,d}
 Plaintext Block, M = Cd mode n
 Cipher text Block, C = Me mode n

10. One Example of RSA algorithm
 According to the algorithm,
 Select two prime number p = 17, q = 11;
 Calculate n = p*q = 17*11 = 187
 Calculate Ø(n) = (p-1)*(q-1) = 16*10 = 160
 Select value of ‘e’ that relatively prime to 160. we choose e = 7.
 Determine d such that ed = 1 mod 160 and the correct value d = 23
because 23*7 = (1*160) +1.
 Public key ,pu = {7,187}
 Private key ,pb = {23,187}
 Now suppose plaintext ,M = 88.
 Ciphertext C = 887 mode 187 = 11
 Plaintext M = 1123 mode 187 = 88

11. Thanks to all