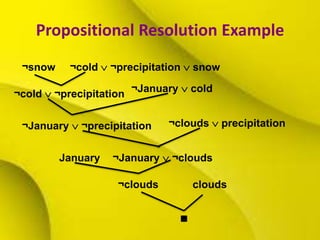
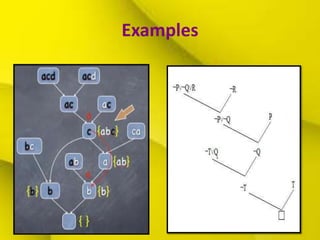
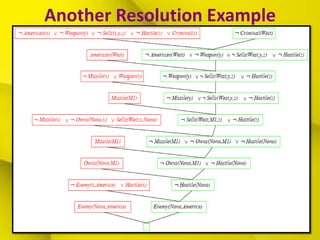
The document discusses resolution, a technique for automated theorem proving in logic. It begins by explaining how to convert first-order logic statements to conjunctive normal form. It then describes the resolution inference rule and how it allows logical statements to be resolved through unification of complementary literals. Additional topics covered include dealing with equality, resolution strategies to improve efficiency, and examples demonstrating how resolution can be used to prove logical statements.

1. Resolution(Decision)
V. Saranya
AP/CSE
Sri Vidya College of Engineering &
Technology, Virudhunagar

2. • Conjunctive normal form
• Resolution inference rule
• Dealing with Equality
• Resolution strategies
• Completeness of resolution
• Theorem provers

3. 1. Conjunctive Normal Form for FOL
x American(x) ˄ Weapon(y) ˄ sells(x,y,z) ˄
Hostile(z) => criminal(x)
CNF:
¬ American (x) ˄ ¬ Weapon(y) ˄ ¬sells(x ,y, z) ˄
¬ hostile(z) ˄ criminal(x)

4. CNF converting Steps
1. Eliminate implication
2. Move ¬ inwards
3. Standardize variables (use different variable)
4. Skolemize (remove existential quantifier)
5. Drop universal quantifiers
6. Distribute ˄ and˄.

5. Converting to CNF
1. Replace implication (A  B) by A  B
2. Move  “inwards”
• x P(x) is equivalent to x P(x) & vice versa
3. Standardize variables
• x P(x)  x Q(x) becomes x P(x)  y Q(y)
4. Skolemize
• x P(x) becomes P(A)
5. Drop universal quantifiers
• Since all quantifiers are now , we don’t need them
6. Distributive Law

6. 2. Resolution Inference rule
• Binary resolution Rule: resolves exactly 2 literals
• Factoring: removal of redundant literals.
• Combination of binary rule & factoring is
“Complete”
• Ex:
• [animal(F(x)) v loves(G(x),x)] and (¬ loves(u,v) v
¬kills(u,v)]
• loves(G(x),x) and ¬ loves(u,v)
• Ɵ = { u/G(x), v/x}  Unifier

7. Example
• Everyone who loves all animal is loved by
someone. Anyone who kills an animal is
loved by no one.
• Nikki loves all animals
• Either nikki or zooro killed the cat, who is
named teena.
• Did zooro kill the cat?

8. 3. Dealing with Equality
Axiomatize Equality:
• Reflexive: x x=x
• Symmetric: x,y x=y, y=x
• Transitive: x,y,z x=y ˄ y=z => x=z
• Predicate name and function names are same
– x,y x=y => (P1(x) P1(y))
• Functional equality.

9. Additional inference rule
• Demodulation
• Para modulation
• Extended unification algorithm

10. 4. Resolution strategies
• To tell proof in a efficient way
1. Unit Preference: ( prefer single literal)
• Evil v devil => ghost
• Devil => ghost
2. Set of support: (subset of sentences)
• Add relevant sentences.
3. Input resolution: combine one of the i/p sentences
with some other sentence.
4. Linear Resolution: complete
Ex: P and Q are 2 predicates. P should be in KB or P is an
ancestor of Q.
5. Subsumption: (elimination)

11. Resolution(decision)
• Convert everything to CNF
• Resolve, with unification
• If resolution is successful, proof succeeds
• If there was a variable in the item to prove, return
variable’s value from unification bindings

12. Resolution (Review)
• Resolution allows a complete inference mechanism (search-
based) using only one rule of inference
• Resolution rule:
– Given: P1  P2  P3 … Pn, and P1  Q1 … Qm
– Conclude: P2  P3 … Pn  Q1 … Qm
Complementary literals P1 and P1 “cancel out”
• To prove a proposition F by resolution,
– Start with F
– Resolve with a rule from the knowledge base (that contains F)
– Repeat until all propositions have been eliminated
– If this can be done, a contradiction has been derived and the original
proposition F must be true.

13. Propositional Resolution Example
• Rules
– Cold and precipitation -> snow
¬cold  ¬precipitation  snow
– January -> cold
¬January  cold
– Clouds -> precipitation
¬clouds  precipitation
• Facts
– January, clouds
• Prove
– snow

14. Propositional Resolution Example
¬snow ¬cold  ¬precipitation  snow
¬cold  ¬precipitation
¬January  cold
¬January  ¬precipitation ¬clouds  precipitation
¬January  ¬cloudsJanuary
¬clouds clouds

15. Examples

16. Another Resolution Example