Relational algebra is a theoretical language that uses tables as variables and produces tables as results, serving as the foundation for higher-level data manipulation languages. It includes operations such as select, project, and join, and it defines set operations like union, intersection, and difference among relations. Each operation has specific requirements, and transformations of tables must maintain compatibility in attributes and data types.

1. Topic : Relational Algebra
Presented By : S.S.Patwardhan
CSE Dept

2. Important Concept
• Relational algebra is similar to high school algebra
except that the variables are tables not numbers and
the results are tables not numbers.

3. Definition
• “Relational algebra is a theoretical language with
operators that are applied on one or two relations to
produce another relation.”Ricardo p. 181
• Both the operands and the result are tables

4. About Relational Algebra
• A procedural language
• Not implemented in native form in DBMS
• Basis for other HL DMLs

5. Operations
• SELECT
• PROJECT
• JOIN

6. OPERATORS
• Can be used in forming complex conditions
• <, <=, >, >=, =, ≠, AND, OR, NOT

7. SELECT
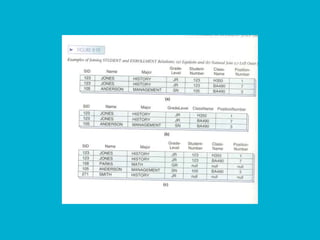
• “The SELECT command is applied to a single table and takes
rows that meet a specific condition copying them into a new
table.” Ricardo p. 182
• Informal general form:
• SELECT tableName WHERE condition [GIVING newTableName]
Ricardo p. 182
• Symbolic form
• σ EmpDept = 10 (EMPLOYEE) Mata-Toledo p. 37

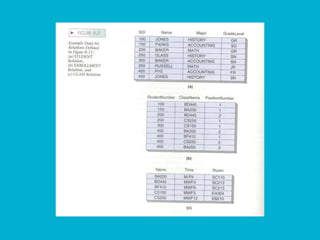
8. PROJECT
• “The PROJECT command also operates on a single
table, but it produces a vertical subset of the table,
extracting the values of specified columns,
eliminating duplicates, and placing the values in a
new table.
• Informal general form:
• PROJECT tableName OVER(colName,…,colName)
[GIVING newTableName] Ricardo p. 183
• Example of symbolic form
• π Location (DEPARTMENT) Mata-Toledo p. 38

9. COMBINING SELECT AND
PROJECT
• Requires two steps
• Operation is not commutative
• Example using general form
• SELECT STUDENT WHERE Major = ‘History’
GIVING Temp
• PROJECT Temp OVER (LastName,
FirstName,StuId) GIVING Result
• Example in symbolic form
• π LastName,FirstName, StuID(σMajor = ‘History’(STUDENT))

10. JOIN
• The JOIN operation is a combination of the
product, selection and possible projection
operations.
• The JOIN of two relations, say A and B,
operates as follows:
• First form the product of A times B.
• Then do a selection to eliminate some tuples (criteria
for the selection are specified as part of the join)
• Then (optionally) remove some attributes by means
of projection.

11. Set Operations on Relations
• CARTESIAN PRODUCT
• UNION
• INTERSECTION
• DIFFERENCE

12. Relation Operations
• Cartesian Product or Product
• The cartesian product of two relations is the
concatenation of every tuple of one relation with every
tuple of a second relations.
• The cartesian product of relation A (having m tuples) and
relation B (having n tuples) has m times n tuples.
• The cartesian product is denoted A X B or A TIMES B.

13. JOIN
• Comes in many flavors
• THETA JOIN – is the most general.
• It is the result of performing a SELECT operation on the product
• Equivalent Examples:
1. Student TIMES Enroll WHERE credits > 50
2. Student TIMES Enroll GIVING Temp
SELECT Temp WHERE credits > 50
3. σ credits> 50 (Student X Enroll)
4. A Xθ B = σ θ (A X B)
• EQUIJOIN is a theta join in which the theta is equality on the common columns
• Equivalent Examples:
1. Student EQUIJOIN Enroll
2. Student XStudent.stuId=Enroll.stuIdEnroll
3. Student Times Enroll GIVING Temp3
SELECT Temp3 WHERE Student.stuId = Enroll.stuID
4. σ Student.stuId=Enroll.stuId (Student X Enroll)
• NATURAL JOIN is an equijoin in which the repeated column is eliminated.
• This is the most common form of the join operation and is usually what is meant by JOIN
• Example:
• tableName1 JOIN tableName2 [ GIVING newTableName]

14. JOIN
• More flavors
• SEMIJOIN –
• “If A and B are tables, then the left-semijoin A|XB, is found by taking the natural join of A and B and
then projecting the result onto the attributes of A.
• The result will be just those tuples of A that participate in the join.” Ricardo, p. 192
• Equivalent Examples:
• Student LEFT-SEMIJOIN Enroll
• Student |X Enroll
• OUTERJOIN
• “This operation is an extension of a THETA JOIN, an EQUIJOIN or a NATURAL JOIN operation.
• When forming any of these joins, any tuple from one of the original tables for which there is no match in
the second table does not enter the result.” Ricardo p. 193
• LEFT OUTER EQUIJOIN & RIGHT OUTER EQUIJOIN
• Are variations of the outer equijoin Ricardo p. 194, 1953

15. Terminology
• For two relations to be union compatible each
relation must have the same number of attributes,
and the attributes in corresponding columns must
come from the same domain.

16. Relation Operations
• Difference
• The difference of two relations is a third relation
containing tuples that occur in the first relation but not in
the second.
• The relations must be union compatible
• A-B is not the same as B-A

17. Relation Operations
• Union
• The union of two relations is formed by adding the tuples
from one relation to those of a second relation to produce
a third relation.
• The order in which the tuples appear in the third relation is
not important.
• Duplicate tuples must be eliminated
• The relations must be union compatible

18. Relation Operations
• Intersection
• The intersection of two relations is a third relation
containing the tuples that appear in both the first and the
second relation.
• The relations must be union compatible

19. Example

20. Attribute Domains

21. Domain Definitions

22. JUNIOR relation (a)
HONOR-STUDENT relation (b)

23. Union of JUNIOR and HONOR-
STUDENT relations

24. Summary of Relational Algebra
Operations

27. References:
Databases Illuminated by Catherine Ricardo, published by Jones and Bartlett in 2004
Fundamentals of Relational Databases by Ramon A. Mata-Toledo and Pauline K.
Cushman, published by McGraw Hill in Schaum’s Outline Series in 2000
Database Processing, Fundamentals, Design, and Implementation, Eighth Edition, by
David M. Kroenke, published by Prentice Hall in 2002