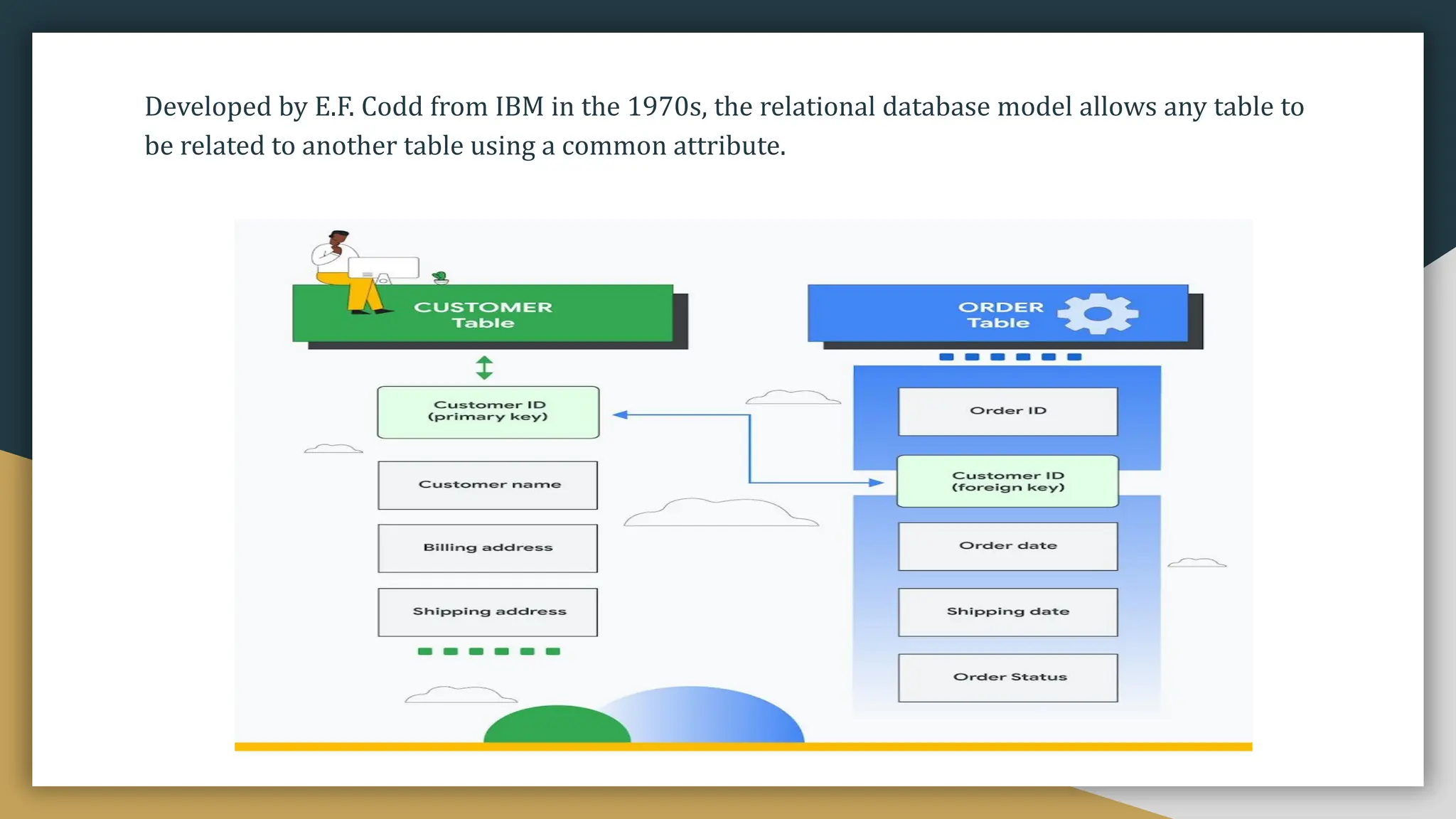
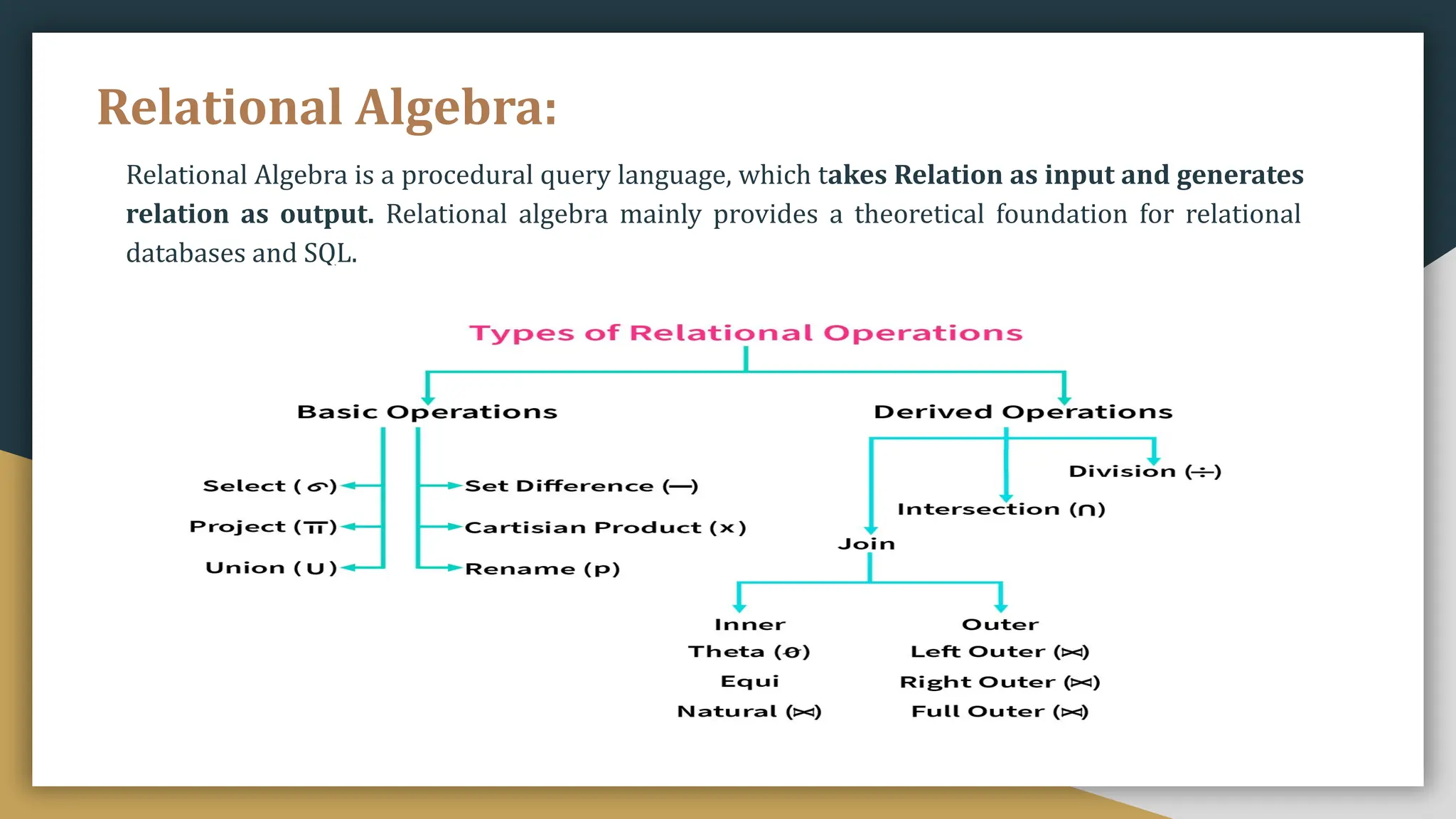
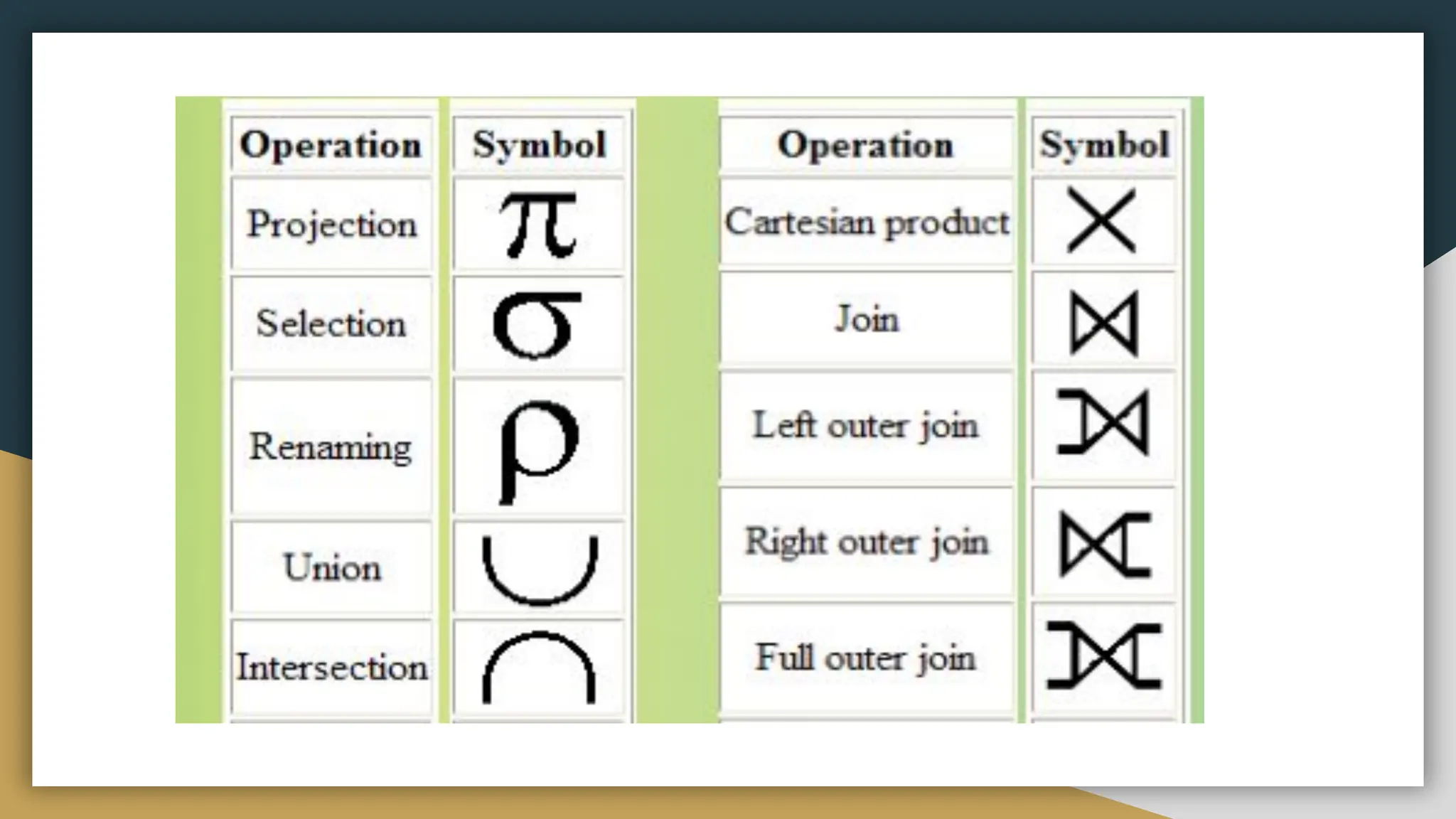
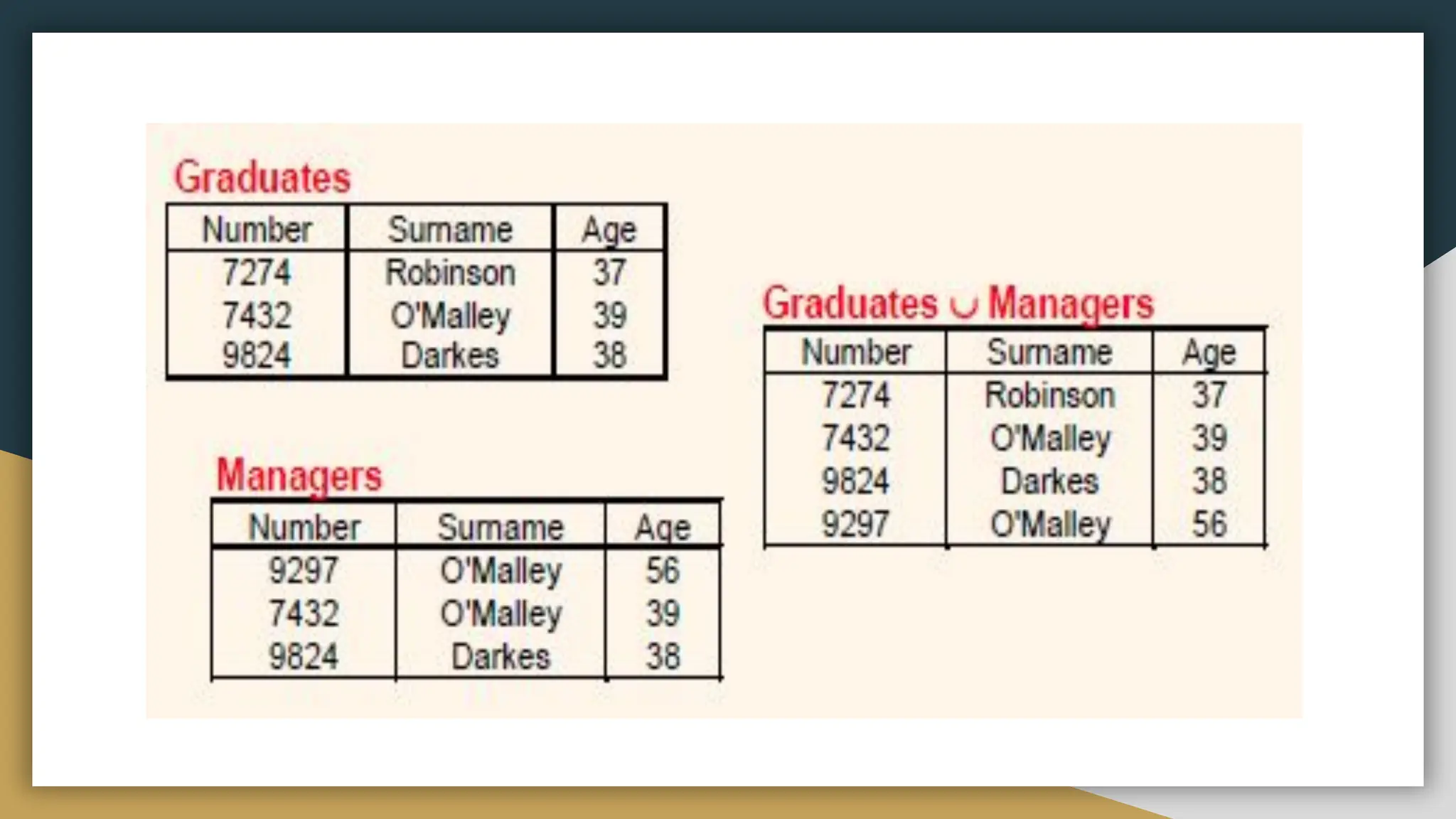
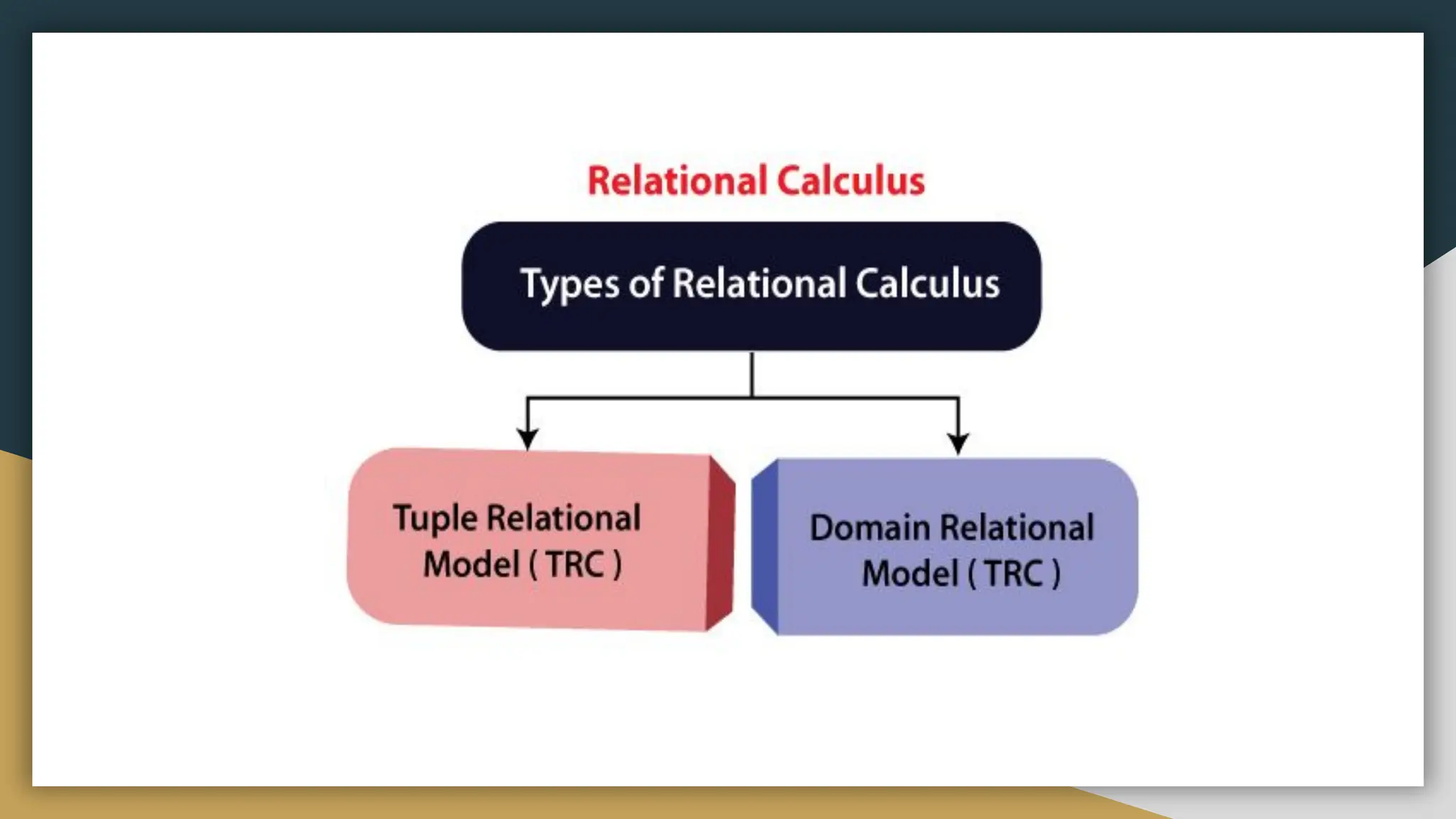
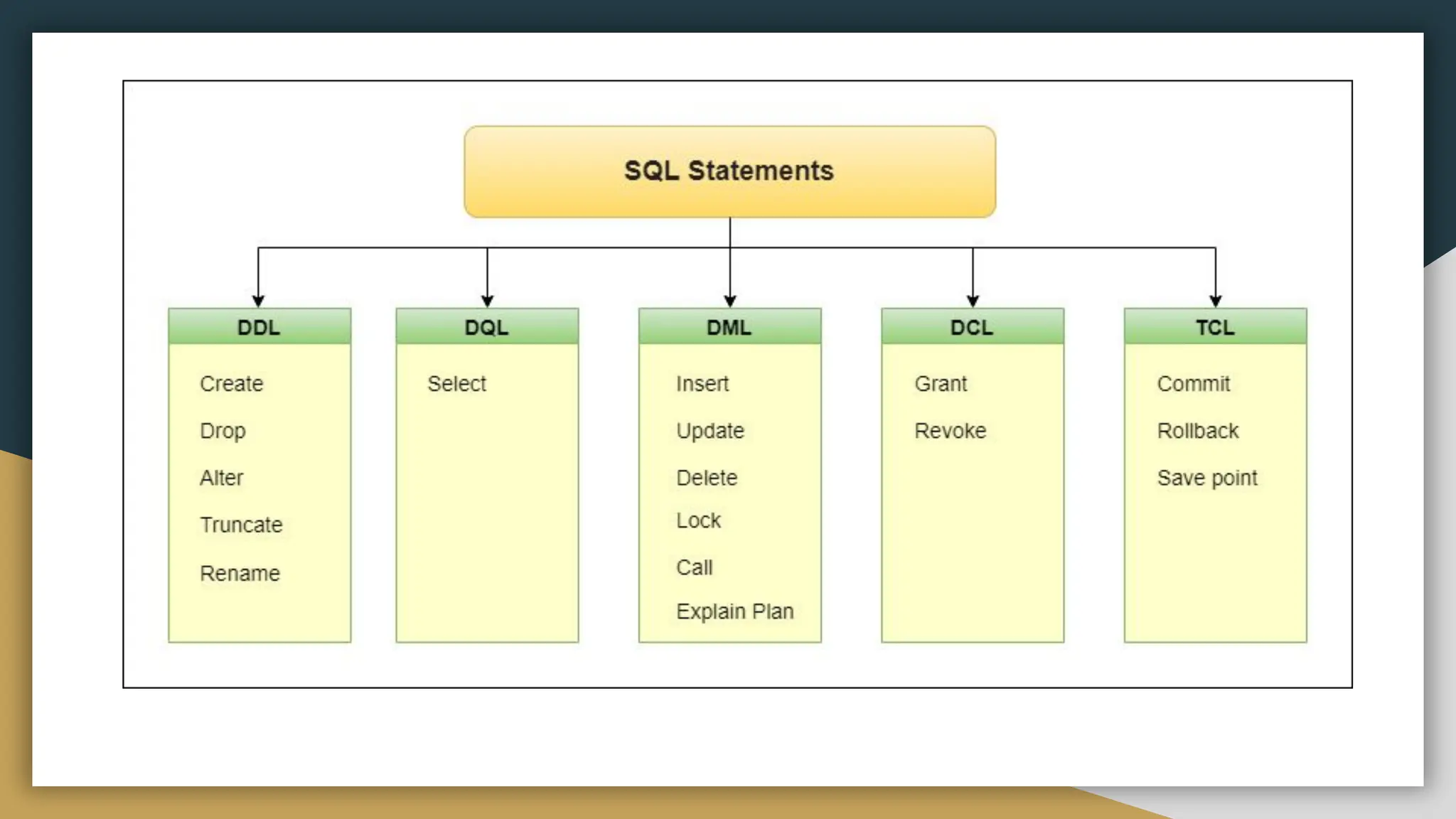
Relational databases organize data into one or more tables made up of rows and columns to show relationships between different data structures. Relationships are logical connections between tables established based on interactions among the tables. Relational algebra provides theoretical foundations for relational databases and SQL through operators like select, project, join, and union that take relations as input and output new relations. Relational calculus is a non-procedural query language that uses predicates and quantifiers to specify what to retrieve from relations rather than how to retrieve it.

1. UNIT-II
Relational Database

2. Relational Database:
A relational database is a collection of information that organizes data in predefined relationships
where data is stored in one or more tables (or "relations") of columns and rows, making it easy to
see and understand how different data structures relate to each other.
Relationships are a logical connection between different tables, established on the basis of
interaction among these tables.
An RDB has the ability to establish links—or relationships–between information by joining
tables, which makes it easy to understand and gain insights about the relationship between various
data points.

3. Developed by E.F. Codd from IBM in the 1970s, the relational database model allows any table to
be related to another table using a common attribute.

4. Relational Algebra:
Relational Algebra is a procedural query language, which takes Relation as input and generates
relation as output. Relational algebra mainly provides a theoretical foundation for relational
databases and SQL.
Queries in relational algebra are performed using
operators.

6. Project (∏)
Project operation is done by Projection Operator which is represented by "pi"(∏). It is used to retrieve
certain attributes(columns) from the table. It is also known as vertical partitioning as it separates the table
vertically. It is also a unary operator. Notation : ∏ a(r)
Where ∏ is used to represent PROJECTION
● r is used to represent RELATION
● a is the attribute list

7. Select (σ)
Select operation (σ) is done by Selection Operator which is represented by "sigma"(σ). It is
used to retrieve tuples(rows) from the table where the given condition is satisfied. It is a unary
operator means it require only one operand.
Notation : σ p(R)Select Operation:
● The select operation selects tuples that satisfy a given predicate.
● It is denoted by sigma (σ).
Notation: σ p(r)
Where σ is used to represent SELECTION
R is used to represent RELATION
p is the logic formula
Example:
σ AGE=20 (STUDENT)
https://www.scaler.com/topics/dbms/relational-algebra-in-dbms/

8. Union operation (υ)
UNION is symbolized by ∪ symbol. It includes all tuples that are in tables A or in B. It also
eliminates duplicate tuples. So, set A UNION set B would be expressed as:
The result <- A ∪ B
For a union operation to be valid, the following conditions must hold –
● R and S must be the same number of attributes.
● Attribute domains need to be compatible.
● Duplicate tuples should be automatically removed.

10. Set Difference (-)
– Symbol denotes it. The result of A – B, is a relation which includes all tuples that are in A but
not in B.
● The attribute name of A has to match with the attribute name in B.
● The two-operand relations A and B should be either compatible or Union compatible.
● It should be defined relation consisting of the tuples that are in relation A, but not in B.

12. Cartesian Product(X) :
Cartesian Product in DBMS is an operation used to merge columns from two relations.
Generally, a cartesian product is never a meaningful operation when it performs alone. However,
it becomes meaningful when it is followed by other operations. It is also called Cross Product or
Cross Join.
Example – Cartesian product
σ column 2
= ‘1’
(A X B)
Output – The above example shows all rows from relation A and B whose column 2 has value 1

14. Rename (ρ):
Rename is a unary operation used for renaming attributes of a
relation.he results of relational algebra are also relations but without
any name. The rename operation allows us to rename the output
relation. 'rename' operation is denoted with small Greek letter rho ρ.
Notation − ρ x
(E)
Where the result of expression E is saved with name of x.

15. JOINS:
Join Operations
Join operation is essentially a cartesian product followed by a selection criterion. Join operation
denoted by ⋈. JOIN operation also allows joining variously related tuples from different
relations.
Types of JOIN:
Various forms of join operation are:
Inner Joins:
● Theta join
● EQUI join
● Natural join
Outer join:
● Left Outer Join
● Right Outer Join
● Full Outer Join

16. INNER JOIN:This is the most common type of join. Inner joins combine records from two
tables whenever there are matching values in a field common to both tables. Theta Join,
Equijoin, and Natural Join are called inner joins.
THETA JOIN:
A theta join is a join that links relations based on a relationship other than equality
between two columns. A theta join could use any operator other than the "equal"
operator.
Syntax: A ⋈θ
B Where ‘theta’ can be any condition like <,>,<=,>=,<> except =.

18. Equi Join:
This is same as Theta Join but the comparison operator is equal. Generally, if the operator of the Theta
Join is equal operator (=), then the join is called as Equi join instead of Theta Join, Here is an example;

20. Natural Join is an Equijoin of two relations over all common attributes. In other words, when joining two tables, join is
done using all common columns. Therefore, explicit Predicate is not required. See the sample given. Note that Common
Attributes are not duplicated.

21. OUTER JOIN:
It is an extension of natural join to deal with missing values of relation.This join type includes
both matching and no matching values from one relation and matching values from the other
relation when two relations are joined. The relation that returns all tuples is determined using
the Symbol used for the operation. If the Symbol is opened for the Left Relation, it is considered as
the relation that returns all tuples.
Outer join:
● Left Outer Join
● Right Outer Join
● Full Outer Join

22. Left Outer Join:
The left outer join is written as R ⟕ S where R and S are relations. The result of the left outer join is
the set of all combinations of tuples in R and S that are equal on their common attribute names, in
addition (loosely speaking) to tuples in R that have no matching tuples in S.
Left outer join = natural join + mismatch/extra tuple of R.

23. For example : Consider the tables Student_Details and Student_Result. Now, if we want to
implement left outer join on these relations, the result will look like:

24. Right Outer Join:
In the right outer join, operation allows keeping all tuple in the right relation. However, if there is
no matching tuple is found in the left relation, then the attributes of the left relation in the join
result are filled with null values.
Right outer join = natural join+ mismatch/extra tuple of R2.

25. For example : Consider the tables Student_Details and Student_Result. Now, if we want to
implement right outer join on these relations, the result will look like:

26. Full outer join:
Full outer join is like a left or right join except that it contains all rows from both tables. In
full outer join, tuples in R that have no matching tuples in S and tuples in S that have no matching
tuples in R in their common attribute name. It is denoted by ⟗.
In a full outer join, all tuples from both relations are included in the result irrespective of the
matching condition.

27. For example : Consider the tables Student_Details and Student_Result. Now, if we want to
implement full outer join on these relations, the result will look like:

28. Intersection:
It displays the common values in R1 & R2. It is denoted by ∩.
Syntax
∏regno
(R1) ∩ ∏regno
(R2)
Consider two sets, A={1,2,4,6} and B={1,2,7}
Intersection of A and B is A ∩ B ={1,2}
Elements that are present in both sets A and B are present in the set obtained by intersection of A and B.
In relational algebra if R1 and R2 are two instances of relation then,
R1 ∩ R2 ={ x | x€ R1 and x € R2}
That is, the intersection of R1 and R2 only those tuples will be present that are in both R1 and R2

29. Example: ∏Name(Subject1) ∩∏ Course(Subject2)
Important points on INTERSECTION Operation:
1. The INTERSECTION operation is commutative, that is : A ∩ B = B ∩ A
2. The INTERSECTION is associative, that means it is applicable to any number of relation.
A ∩ ( B ∩ C ) = ( A ∩ B ) ∩ C
3. INTERSECTION can be formed using UNION and MINUS as follows:
A ∩ B = ((A ∪ B) - (A - B)) - (B - A)

30. DIVISION Operation:(/)
The Divition Operation is defined on two relation r(U1) and s(U2) where U2 is the subset of U1 and s is not an
empty relation:
r÷s={t∣t∈r(U1−U2)∧satisfy}
Where satisfy=∀ts∈s(∃tr∈r(tr[U2]=ts∧tr[U1−U2]=t))
This means that for a tuple t to appear in the result of Division, the values in t must appear in r in combination
with every tuple in s.
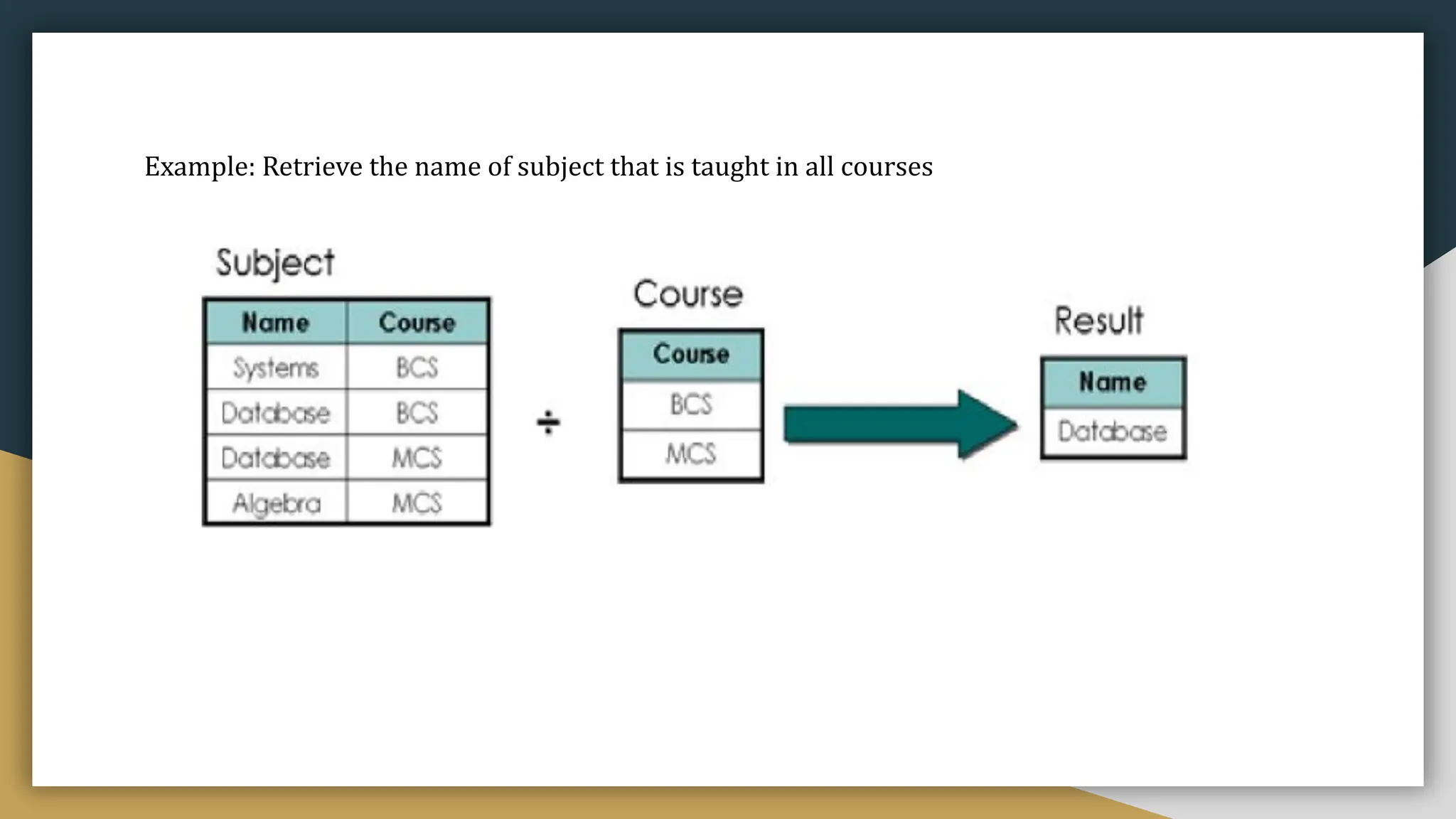
The Division is very useful for a special kind of query such as “ Retrieve the name of the student who
enrolls in all course teach by Professor Ba”
● Producing the result of the Division operation
○ Consider each subset of tuple in r that match on t[U1 – U2]
○ For this subset of tuples, take the values t[U2] from each. If this covers all tuples in s then add
t[U1 – U2]in the result.

31. Example: Retrieve the name of subject that is taught in all courses

32. Relational Calculus:
There is an alternate way of formulating queries known as Relational Calculus. Relational calculus is a
non-procedural query language. In the non-procedural query language, the user is concerned with the
details of how to obtain the end results. The relational calculus tells what to do but never explains how to
do. Most commercial relational languages are based on aspects of relational calculus including SQL-QBE
and QUEL.
Why it is called Relational Calculus?
It is based on Predicate calculus, a name derived from branch of symbolic language. A predicate is a
truth-valued function with arguments. On substituting values for the arguments, the function result in
an expression called a proposition. It can be either true or false.

33. Many of the calculus expressions involves the use of Quantifiers. There are two types of
quantifiers:
● Universal Quantifiers: The universal quantifier denoted by ∀ is read as for all which
means that in a given set of tuples exactly all tuples satisfy a given condition.
● Existential Quantifiers: The existential quantifier denoted by ∃ is read as for all which
means that in a given set of tuples there is at least one occurrences whose value satisfy a
given condition.
Before using the concept of quantifiers in formulas, we need to know the concept of Free and
Bound Variables.
A tuple variable t is bound if it is quantified which means that if it appears in any occurrences a
variable that is not bound is said to be free.

35. Tuple Relational Calculus (TRC):
t is a non-procedural query language which is based on finding a number of tuple variables also
known as range variable for which predicate holds true. It describes the desired information
without giving a specific procedure for obtaining that information. The tuple relational calculus
is specified to select the tuples in a relation. In TRC, filtering variable uses the tuples of a relation.
The result of the relation can have one or more tuples.
Notation: A Query in the tuple relational calculus is expressed as following notation
1. {T | P (T)} or {T | Condition (T)}
Where T is the resulting tuples ,
P(T) is the condition used to fetch T.

36. For example:
1. { T.name | Author(T) AND T.article = 'database' }
Output: This query selects the tuples from the AUTHOR relation. It returns a tuple with 'name'
from Author who has written an article on 'database'.
TRC (tuple relational calculus) can be quantified. In TRC, we can use Existential (∃) and
Universal Quantifiers (∀).
For example:
1. { R| ∃T ∈ Authors(T.article='database' AND R.name=T.name)}
Output: This query will yield the same result as the previous one.

37. Customer_id Name Zip code
1 Rohit 12345
2 Rahul 13245
3 Rohit 56789
4 Amit 12345.
Customer Table
Example 1: Write a TRC query to get all the data of customers whose zip code is 12345.
TRC Query: {t | t ∈ Customer ∧ t.Zipcode = 12345} or TRC Query: {t | Customer(t) ∧ t[Zipcode] = 12345 }
Workflow of query - The tuple variable "t" will go through every tuple of the Customer table. Each row will check
whether the Cust_Zipcode is 12345 or not and only return those rows that satisfies the Predicate expression
condition.
The TRC expression above can be read as "Return all the tuple which belongs to the Customer Table and whose
Zipcode is equal to 12345."
Customer_id Name Zip code
1 Rohit 12345
4. Amit 12345
RESULT OF THE QUERY

38. 2. Domain Relational Calculus (DRC):
The second form of relation is known as Domain relational calculus. In domain relational calculus,
filtering variable uses the domain of attributes. Domain relational calculus uses the same operators
as tuple calculus. It uses logical connectives ∧ (and), ∨ (or) and ┓ (not). It uses Existential (∃) and
Universal Quantifiers (∀) to bind the variable. The QBE or Query by example is a query language
related to domain relational calculus.
Notation: { a1, a2, a3, ..., an | P (a1, a2, a3, ... ,an)}
Where a1, a2 are attributes
P stands for formula built by inner attributes

39. Domain Relational Calculus uses domain Variables to get the column values required from the
database based on the predicate expression or condition.
The Domain relational calculus expression syntax:
{<x1,x2,x3,x4...> | P(x1,x2,x3,x4...)}
where,
<x1,x2,x3,x4...> are domain variables used to get the column values required, and
P(x1,x2,x3...) is predicate expression or condition.

40. Customer Table Result:
Customer_id Name Zip code
1 Rohit 12345
2 Rahul 13245
3 Rohit 56789
4 Amit 12345
Customer_id Name Zip code
1 Rohit 12345
4 Amit 12345
Example 1: Write a DRC query to get the data of all customers with Zip code 12345.
DRC query: {<x1,x2,x3> | <x1,x2> ∈ Customer ∧ x3 = 12345 }
Workflow of Query: In the above query x1,x2,x3 (ordered) refers to the attribute or column which we
need in the result, and the predicate condition is that the first two domain variables x1 and x2 should
be present while matching the condition for each row and the third domain variable x3 should be equal
to 12345.

41. SQL:
● SQL stands for Structured Query Language
● SQL lets you access and manipulate databases
● SQL became a standard of the American National Standards Institute (ANSI) in 1986, and of the
International Organization for Standardization (ISO) in 1987
● SQL can execute queries against a database
● SQL can retrieve data from a database
● SQL can insert records in a database
● SQL can update records in a database
● SQL can delete records from a database
● SQL can create new databases
● SQL can create new tables in a database
● SQL can create stored procedures in a database
● SQL can create views in a database
● SQL can set permissions on tables, procedures, and views

42. Following are the four different types of languages or commands which are widely used in
SQL queries:
1. DDL (Data Definition Language)
2. DML (Data Manipulation Language)
3. DCL (Data Control Language)
4. TCL (Transaction Control Language)

44. DDL (Data Definition Language)
DDL or Data Definition Language actually consists of the SQL commands that can be used to define the
database schema. It simply deals with descriptions of the database schema and is used to create and
modify the structure of database objects in the database. DDL is a set of SQL commands used to create,
modify, and delete database structures but not data. These commands are normally not used by a
general user, who should be accessing the database via an application.
List of DDL commands:
● CREATE: This command is used to create the database or its objects (like table, index, function,
views, store procedure, and triggers).
● DROP: This command is used to delete objects from the database.
● ALTER: This is used to alter the structure of the database.
● TRUNCATE: This is used to remove all records from a table, including all spaces allocated for the
records are removed.
● COMMENT: This is used to add comments to the data dictionary.
● RENAME: This is used to rename an object existing in the database.

45. 1. CREATE TABLE:
In Oracle, CREATE TABLE statement is used to create a new table in the database.
To create a table, you have to name that table and define its columns and datatype for each column.
Syntax:
CREATE TABLE table_name
( column1 datatype [ NULL | NOT NULL ],
column2 datatype [ NULL | NOT NULL ],
...
column_n datatype [ NULL | NOT NULL ]
);
CREATE TABLE Example
CREATE TABLE customers
( customer_id number(10) NOT NULL,
customer_name varchar2(50) NOT
NULL,
city varchar2(50)
);

46. 1. CREATE TABLE AS STATEMENT:
The CREATE TABLE AS statement is used to create a table from an existing table by copying the columns of
existing table.
Syntax:
CREATE TABLE new_table
AS (SELECT * FROM old_table);
CREATE TABLE Example
CREATE TABLE newcustomers
AS (SELECT * FROM customers
WHERE customer_id < 5000);
Create Table Example: copying selected columns of another table :
Syntax:
CREATE TABLE new_table
AS (SELECT column_1, column2, ... column_n
FROM old_table);
CREATE TABLE Example
CREATE TABLE newcustomers2
AS (SELECT customer_id, customer_name
FROM customers
WHERE customer_id < 5000);

47. CREATE TABLE AS Statement:
https://www.javatpoint.com/oracle-create-table-as