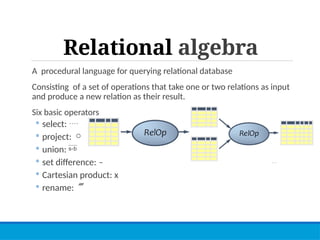
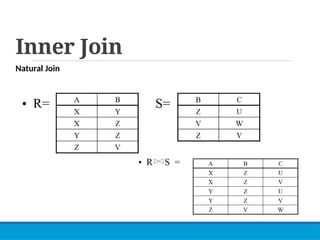
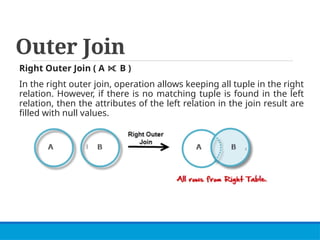
This lecture covers relational algebra, a procedural query language used for managing relational databases, and distinguishes between procedural and non-procedural query languages. It details various relational algebra operations such as selection, projection, union, and various types of joins, including inner and outer joins. Additionally, it provides examples and assignments to reinforce understanding of the subject matter.

1. Lecture #12
Relational
Algebra
Prepared by : engr. Soonh taj 1

2. In this Lecture you will Learn about:
Query Languages Types
Relational Algebra
Relational Algebra Operators
01/30/2025 2

3. Query Languages Types
1. Procedural Query Language
-Relational Algebra
2. Non-Procedural Query Language
-Tuple relational calculus and domain relational calculus
01/30/2025 3

4. Query Languages Types
1. Procedural Query Language: (Specifies how to retrieve
data.)
•In a procedural query language, you specify step-by-step
instructions for how to retrieve the desired data from the
database.
•Queries are expressed as sequences of operations that are
executed in a particular order.
•Relational algebra is an example of a procedural query
language commonly used in relational databases. It defines
operations like selection, projection, join, etc., and queries are
formulated by composing these operations in a specific
sequence.
01/30/2025 4

5. Query Languages Types
2. Non-Procedural Query Language: (Specifies what data to retrieve.)
•In a non-procedural query language, you specify what data you want to
retrieve without specifying how to retrieve it.
•Queries are expressed as logical statements or declarative expressions
that describe the desired result set.
•Tuple relational calculus and domain relational calculus are examples of
non-procedural query languages used in relational databases. Instead of
specifying a sequence of operations, queries are formulated as logical
conditions that the desired data must satisfy.
01/30/2025 5

6. Query Languages Types
1. Relational Algebra: Relational algebra is a procedural query language
that defines a set of operations that can be applied to relations (tables)
in a relational database. These operations include selection, projection,
Cartesian product, join, union, intersection, and difference, among
others. It provides a way to express queries as a series of operations on
relations.
01/30/2025 6

7. Query Languages Types
2. Tuple Relational Calculus: Tuple relational calculus is a non-procedural
query language that defines queries in terms of logical formulas. Instead
of specifying a sequence of operations to retrieve data, tuple relational
calculus describes what data should be retrieved. It uses variables and
quantifiers to specify conditions that the desired tuples must satisfy.
01/30/2025 7

8. Query Languages Types
3. Domain Relational Calculus: Domain relational calculus is another
non-procedural query language that operates similarly to tuple relational
calculus but focuses on specifying conditions on the attributes or
domains of relations rather than on individual tuples. It also uses
variables and quantifiers to express conditions that the desired data
must satisfy.
01/30/2025 8

9. A procedural language for querying relational database
Consisting of a set of operations that take one or two relations as input
and produce a new relation as their result.
Six basic operators
◦ select: 
◦ project: 
◦ union: 
◦ set difference: –
◦ Cartesian product: x
◦ rename: 
Relational algebra

11. Select Operation
The select operation selects tuples that satisfy a given predicate.
Notation: p(r)
p is called the selection predicate
Example: select those tuples of the instructor relation where the instructor is in
the “Physics” department.
◦ Query
dept_name=“Physics” (instructor)
◦ Result

12. Select Operation

13. Select Operation (Cont.)
We allow comparisons using
=, , >, . <.  (in the selection predicate.)
We can combine several predicates into a larger predicate by using the
connectives:
 (and),  (or),  (not)
Example: Find the instructors in Physics with a salary greater 90,000
 dept_name=“Physics” salary > 90,000 (instructor)
Then select predicate may include comparisons between two attributes.
◦ Example: Find all departments whose name is the same as their building name:
◦  dept_name=building (department)

14. Project Operation
A unary operation that returns a set of chosen columns.
Notation:
 A1,A2,A3 ….Ak
(r)
where A1, A2 are attribute names and r is a relation name.
The result is defined as the relation of k columns obtained by erasing the columns
that are not listed
Duplicate rows removed from result, since relations are sets

15. Project Operation
(Cont.)
Example: eliminate the dept_name attribute of instructor
Query:
ID, name, salary (instructor)
Result:

16. Project Operation
(Cont.)

17. The Assignment Operation
It is convenient at times to write a relational-algebra expression by assigning parts of
it to temporary relation variables.
The assignment operation is denoted by  and works like assignment in a
programming language.
Example: Find all instructor in the “Physics” and Music department.
Physics   dept_name=“Physics” (instructor)
Music   dept_name=“Music” (instructor)
Physics  Music
With the assignment operation, a query can be written as a sequential program
consisting of a series of assignments followed by an expression whose value is
displayed as the result of the query.

18. Composition of Relational Operations
The result of a relational-algebra operation is relation and therefore of
relational-algebra operations can be composed together into a relational-algebra
expression.
Consider the query -- Find the names of all instructors in the Physics
department.
name( dept_name =“Physics” (instructor))
Instead of giving the name of a relation as the argument of the projection
operation, we give an expression that evaluates to a relation.

19. Set Union Operation
The union operation allows us to combine two relations
Notation: r  s
For r  s to be valid.
1. r, s must have the same arity (same number of attributes)
2. The attribute domains must be compatible (example: 2nd
column of r deals with the same type of values as does the 2nd
column of s)
Example: to find all courses taught in the Fall 2017 semester, or in the Spring
2018 semester, or in both
course_id ( semester=“Fall” Λ year=2017 (section)) 
course_id ( semester=“Spring” Λ year=2018 (section))

20. Set Union Operation

21. Set-Intersection Operation
The set-intersection operation allows us to find tuples that are in
both the input relations.
Notation: r  s
Assume:
◦ r, s have the same attributes
◦ attributes of r and s are compatible
Example: Find the set of all courses taught in both the Fall 2017
and the Spring 2018 semesters.
course_id ( semester=“Fall” Λ year=2017 (section)) 
course_id ( semester=“Spring” Λ year=2018 (section))

22. Set-Intersection Operation

23. Set Difference Operation
The set-difference operation allows us to find tuples that are in one relation but
are not in another.
Notation r – s
Set differences must be taken between compatible relations.
◦ r and s must have the same attribute
◦ attribute domains of r and s must be compatible
Example: to find all courses taught in the Fall 2017 semester, but not in the Spring
2018 semester
course_id ( semester=“Fall” Λ year=2017 (section)) −
course_id ( semester=“Spring” Λ year=2018 (section))

24. Set Difference Operation

25. Set Operations

26. The Rename Operation
The results of relational-algebra expressions do not have a name that we can use to
refer to them. The rename operator,  , is provided for that purpose
The expression:
x (E)
returns the result of expression E under the name x
Another form of the rename operation:
x(A1,A2, .. An) (E)

27. The Rename Operation

28. The Rename Operation

29. Equivalent Queries
There is more than one way to write a query in relational algebra.
Example: Find information about courses taught by instructors in the Physics
department with salary greater than 90,000
Query 1
 dept_name=“Physics” salary > 90,000 (instructor)
Query 2
 dept_name=“Physics” ( salary > 90.000 (instructor))
The two queries are not identical; they are, however, equivalent -- they give the same
result on any database.

30. Cartesian-Product Operation
The Cartesian-product operation (denoted by X) allows us to combine information from
any two relations.
Example: the Cartesian product of the relations instructor and teaches is written as:
instructor X teaches
We construct a tuple of the result out of each possible pair of tuples: one from the
instructor relation and one from the teaches relation
Since the instructor ID appears in both relations we distinguish between these attribute by
attaching to the attribute the name of the relation from which the attribute originally came.
◦ instructor.ID
◦ teaches.ID

31. Cartesian-Product Operation

32. Cartesian-Product Operation
The instructor X teaches table
X

33. Join Operation
The Cartesian-Product
instructor X teaches
associates every tuple of instructor with every tuple of teaches.
◦ Most of the resulting rows have information about instructors who did NOT
teach a particular course  meaningless
To get only those tuples of “instructor X teaches “ that pertain to instructors and
the courses that they taught, we write:
 instructor.id = teaches.id (instructor x teaches ))
◦ We get only those tuples of “instructor X teaches” that pertain to instructors
and the courses that they taught.

34. Join Operation
The table corresponding to:  instructor.id = teaches.id (instructor x teaches))
X  instructor.id = teaches.id

35. Join Operation (Cont.)
The join operation allows us to combine a select operation and a Cartesian-
Product operation into a single operation.
Consider relations r (R) and s (S)
Let “theta” be a predicate on attributes in the schema R “union” S. The join
operation r s is defined as follows:
Thus
 instructor.id = teaches.id (instructor x teaches ))
Can equivalently be written as
instructor Instructor.id = teaches.id teaches.

36. Types of Joins

37. Inner Joins
Inner Join
In an inner join, only those tuples that satisfy the matching
criteria are included, while the rest are excluded. Let’s study
various types of Inner Joins:

38. Inner Join
Theta Join
The general case of JOIN operation is called a Theta join. It is denoted by
symbol θ
Theta join can use any conditions in the selection criteria.

39. Inner Join
Theta Join

40. Inner Join
Natural join
It can only be performed if there is a common attribute (column) between the relations. The
name and type of the attribute must be same.
Notation: R1 R2
Input Schema: R1(A1, …, An), R2(B1, …, Bm)
Output Schema: S(C1,…,Cp)
◦ Where {C1, …, Cp} = {A1, …, An} U {B1, …, Bm}
Meaning: combine all pairs of tuples in R1 and R2 that agree on the attributes:
◦ {A1,…,An} {B1,…, Bm} (called the join attributes)
Equivalent to a cross product followed by selection
Example Employee Dependents


41. Inner Join
Natural Join

42. Outer Join
In an outer join, along with tuples that satisfy the matching criteria, we also
include some or all tuples that do not match the criteria.
Left Outer Join(A B)
⟕
In the left outer join, operation allows keeping all tuple in the left relation.
However, if there is no matching tuple is found in right relation, then the
attributes of right relation in the join result are filled with null values.

43. Outer Join
Left Outer Join(A B)
⟕

44. Outer Join
Right Outer Join ( A B )
⟖
In the right outer join, operation allows keeping all tuple in the right
relation. However, if there is no matching tuple is found in the left
relation, then the attributes of the left relation in the join result are
filled with null values.

45. Outer Join
Right Outer Join ( A B )
⟖

46. Outer Join
Full Outer Join ( A B)
⟗
In a full outer join, all tuples from both relations are included in the result,
irrespective of the matching condition.

47. Semi Join
Semi Join ( A ⋉ B)
A semi-join operation in relational algebra combines two tables and
returns only the rows from the first table (the left-hand side) that
have matching values in the second table (the right-hand side). The
resulting table contains all the attributes of the first table.

48. Semi Join
Semi Join ( A ⋉ B)
A semi-join operation in relational algebra combines two tables and
returns only the rows from the first table (the left-hand side) that
have matching values in the second table (the right-hand side). The
resulting table contains all the attributes of the first table.

49. Anti Join
Anti Join ( A ▷ B)
An anti-join operation in relational algebra combines two tables and
returns only the rows from the first table (the left-hand side) that do
not have matching values in the second table (the right-hand side).
It excludes the rows that have matching values in the second table.

50. Anti Join
Anti Join ( A ▷ B)
An anti-join operation in relational algebra combines two tables and
returns only the rows from the first table (the left-hand side) that do
not have matching values in the second table (the right-hand side).
It excludes the rows that have matching values in the second table.

51. Division Operator

52. Example - Division
Identify all clients who have viewed all properties with three
rooms.
(clientNo, propertyNo(Viewing)) 
(propertyNo(rooms = 3 (PropertyForRent)))

53. Relational Algebra Operators-
Quick Review

54. Relational Algebra Operators-
Quick Review

55. Relational Algebra Operators-
Quick Review

56. Considering above schema, state what the following queries compute:

57. Answers

58. Assignment
Consider the following schema:
Suppliers(sid: integer, sname: string, address: string)
Parts(pid: integer, pname: string, color: string)
Catalog(sid: integer, pid: integer, cost: real)

59. Assignment
1. Find the sids of suppliers who supply every part.
2. Find the sids of suppliers who supply every red part.
3. Find the sids of suppliers who supply every red or green part.
4. Find the sids of suppliers who supply every red part or supply every
green part.
5. Find pairs of sids such that the supplier with the first sid charges
more for some part than the supplier with the second sid.
6. Find the pids of parts supplied by at least two different suppliers.

60. Assignment
7. Find the names of suppliers who supply some red part.
8. Find the sids of suppliers who supply some red or green part.
9. Find the sids of suppliers who supply some red part or are at Street
No.22 Sadar Karachi.
10. Find the sids of suppliers who supply some red part and some green
part.

61. Assignment
1.Find the sids of suppliers who supply every part.

62. Assignment
2. Find the sids of suppliers who supply every red part.

63. Assignment
3. Find the sids of suppliers who supply every red or green part.

64. Assignment
4. Find the sids of suppliers who supply every red part or supply every
green part.

65. Assignment
5. Find pairs of sids such that the supplier with the first sid charges more
for some part than the supplier with the second sid.

66. Assignment
6. Find the pids of parts supplied by at least two different suppliers.

67. Assignment
7.Find the names of suppliers who supply some red part.

68. Assignment
8. Find the sids of suppliers who supply some red or green part.

69. Assignment
9.Find the sids of suppliers who supply some red part or are at Street
No.22 Sadar Karachi.

70. Assignment
10. Find the sids of suppliers who supply some red part and some green
part.