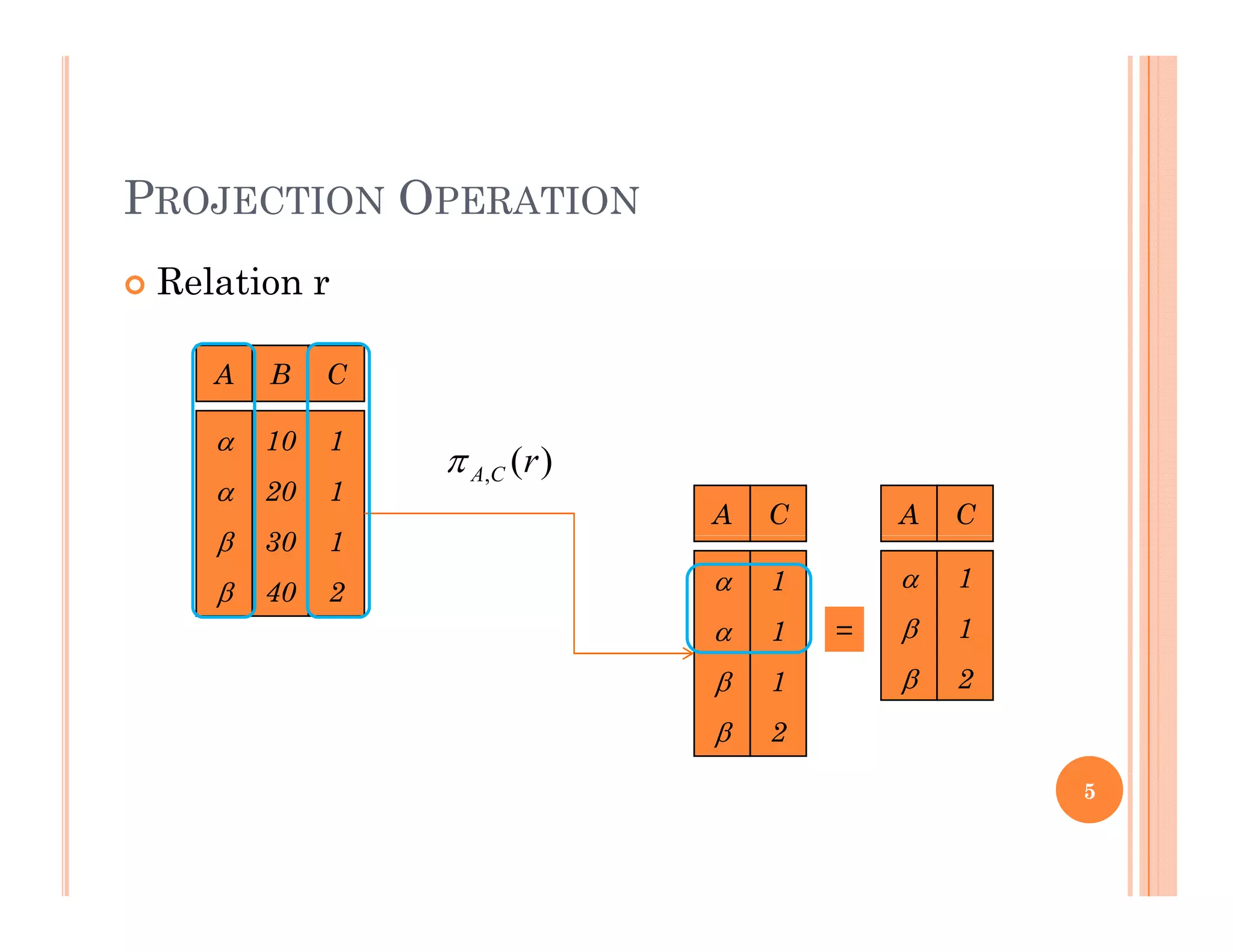
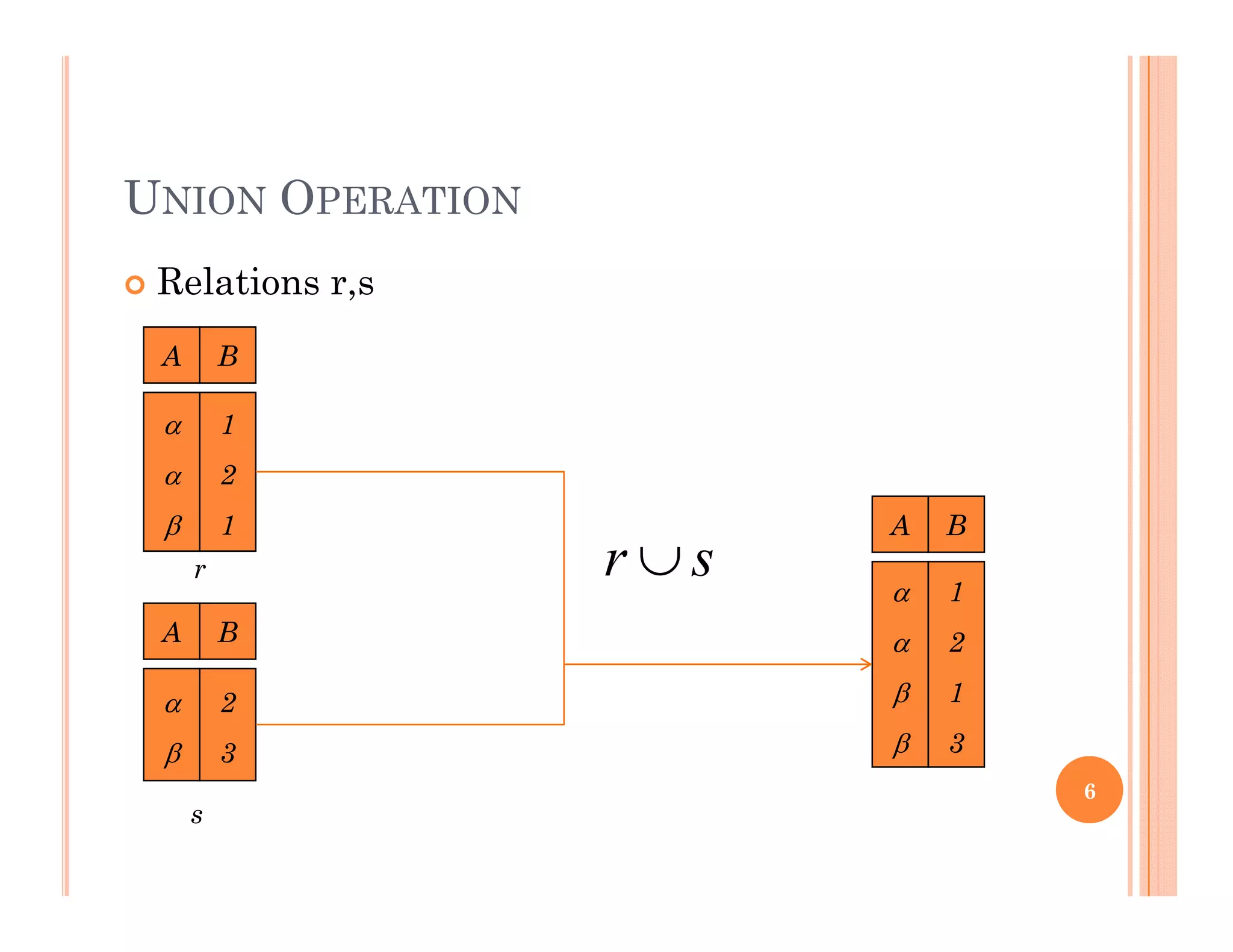
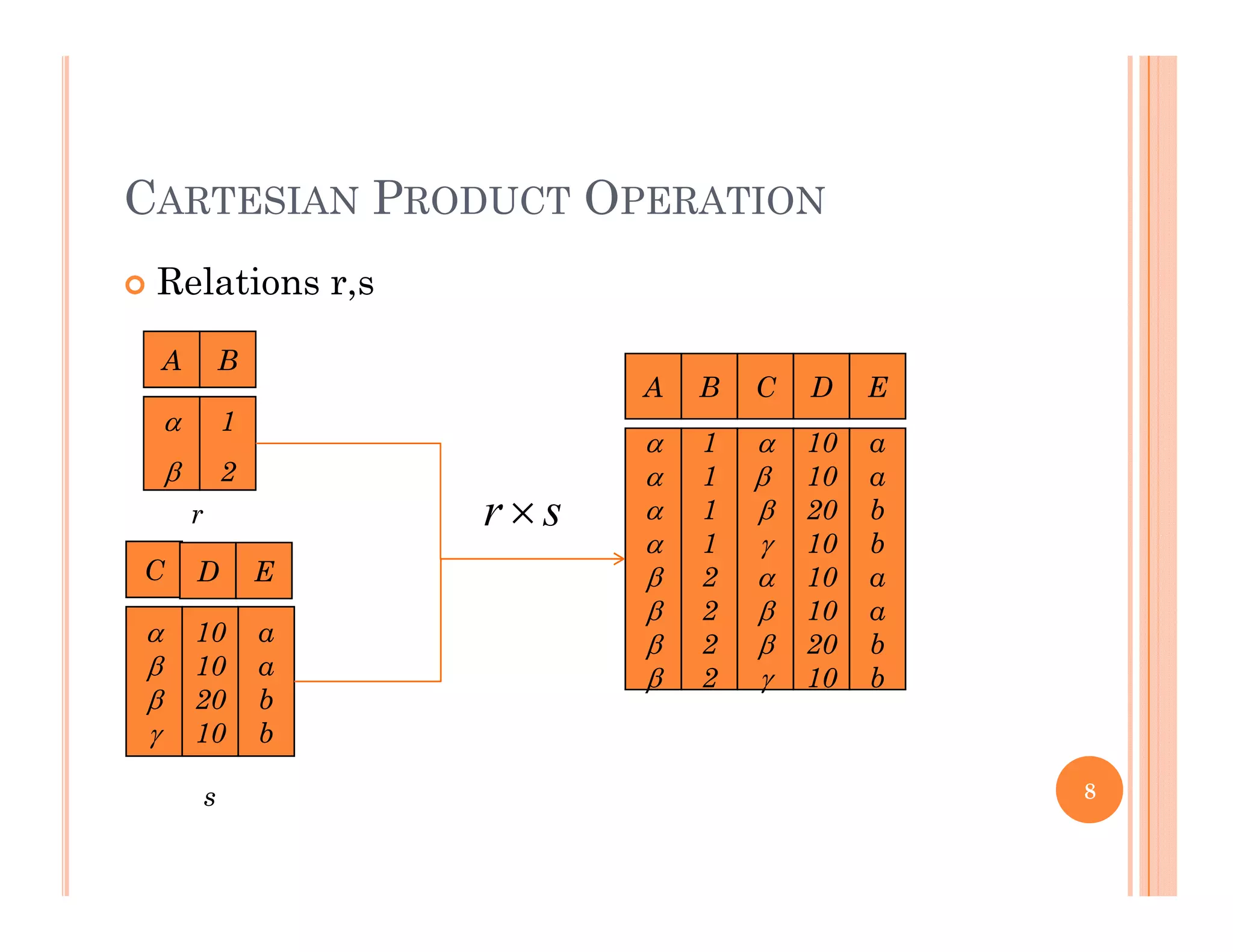
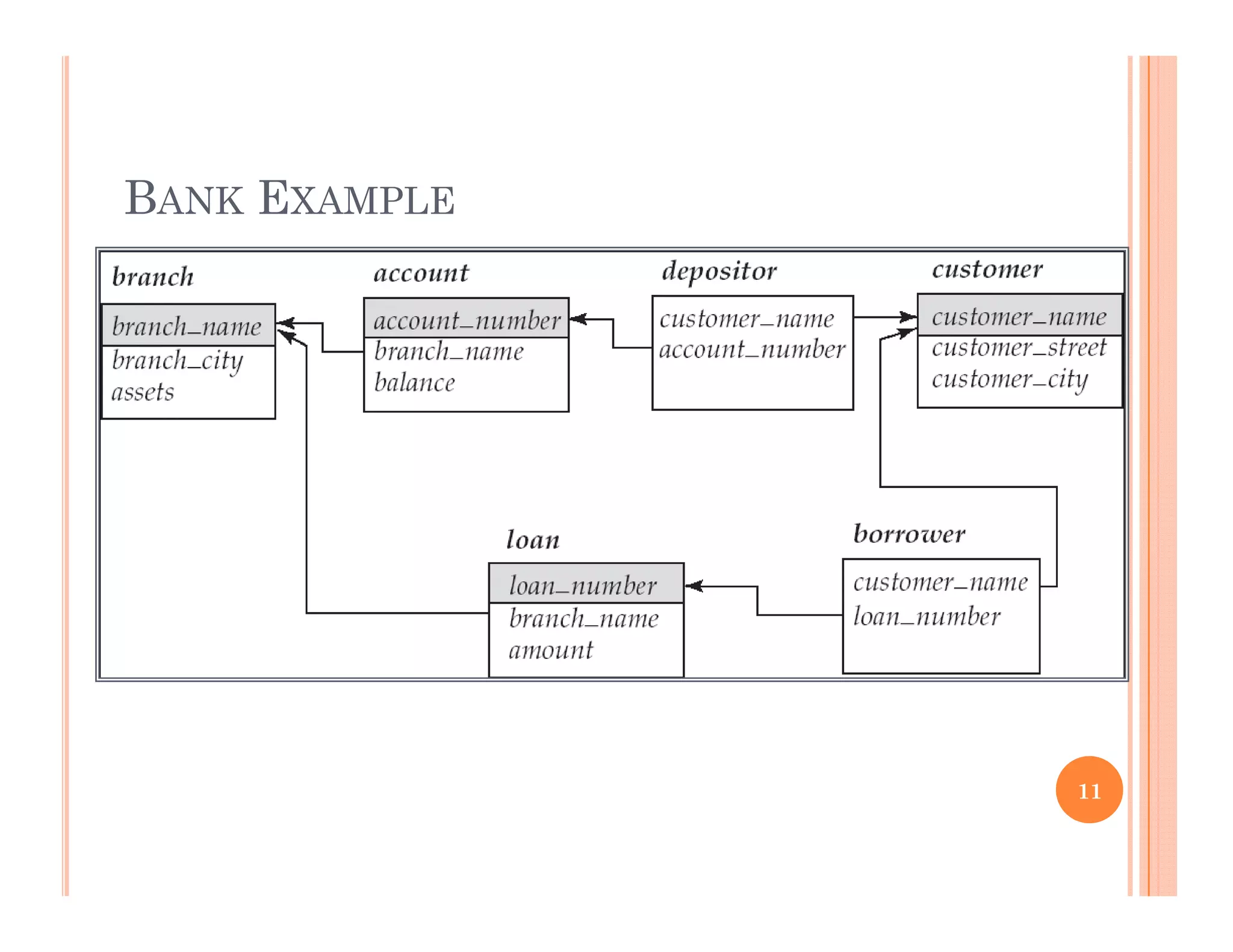
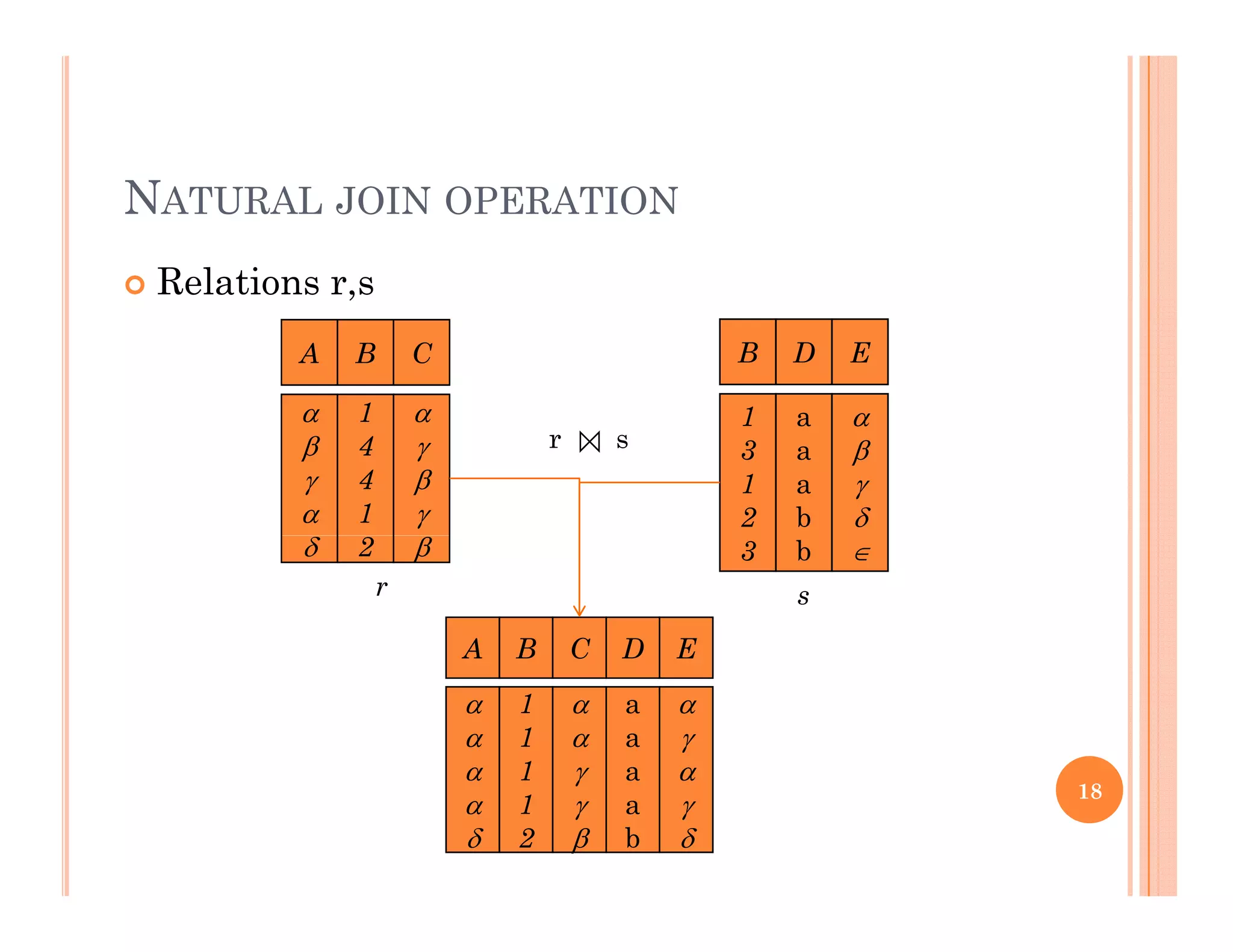
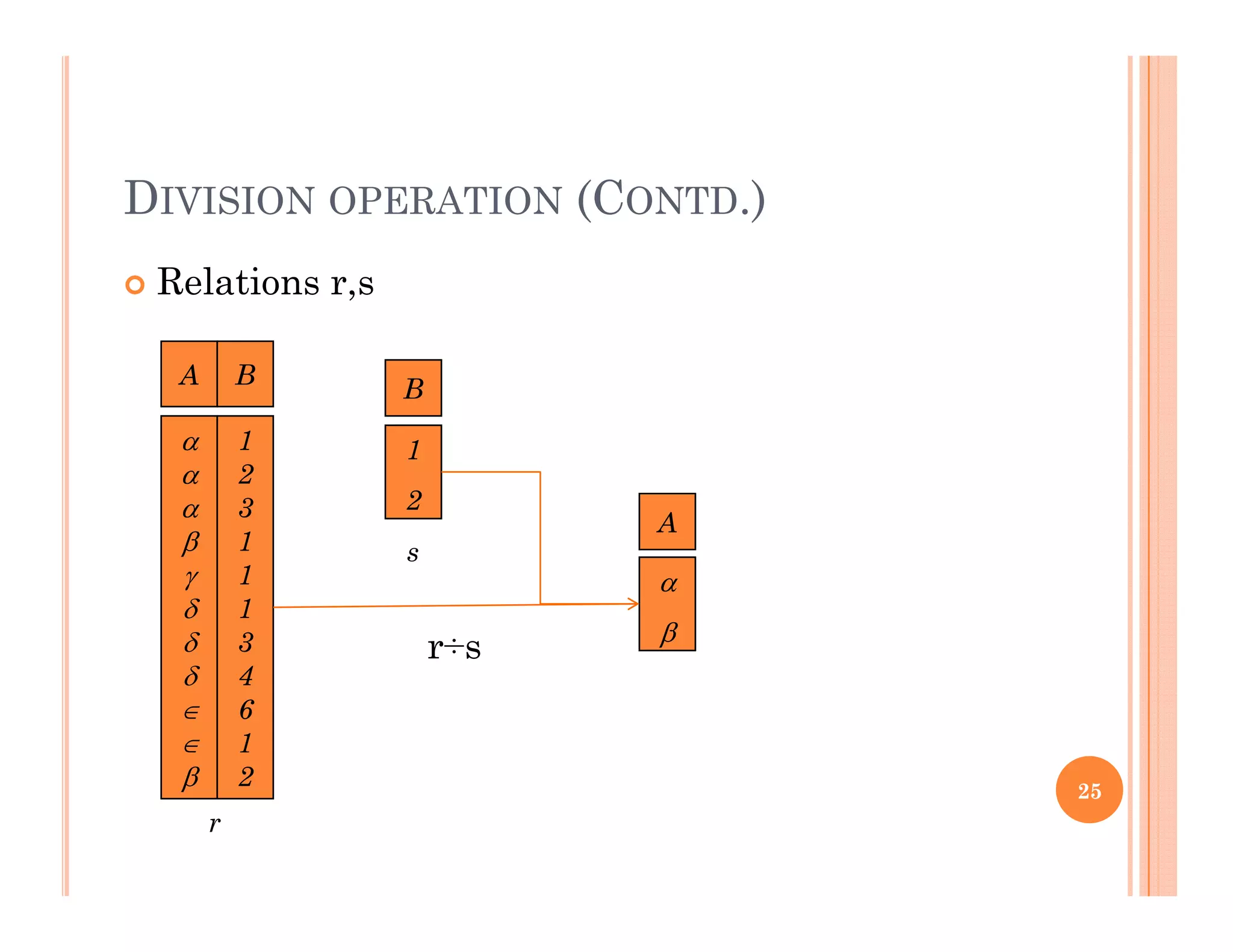
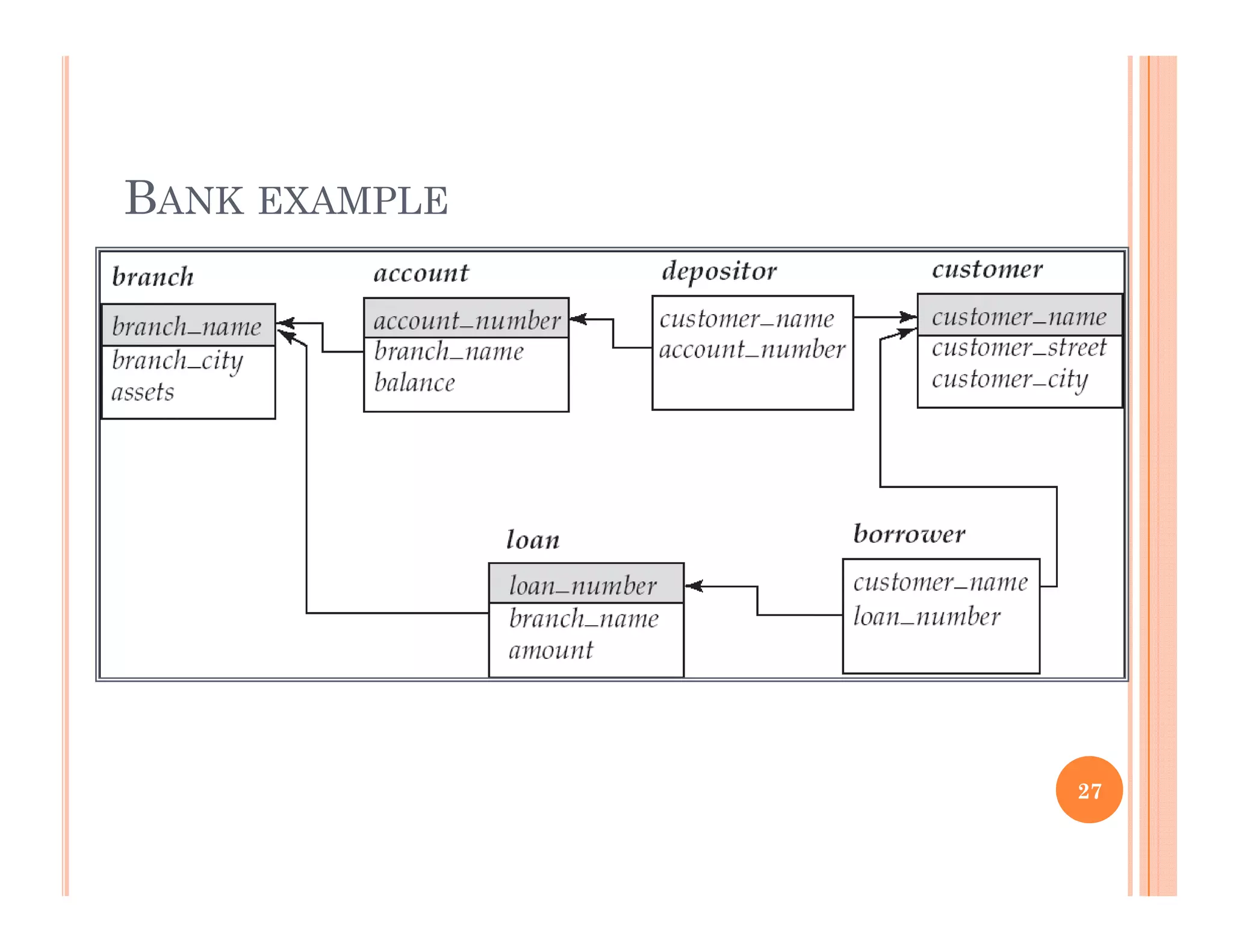
This document discusses query languages and relational algebra operations. It introduces relational algebra as a procedural query language. The basic relational algebra operations are selection, projection, union, set difference, cartesian product, and rename. Examples are provided to illustrate each operation. Additional operations like join, outer join, division and aggregation are also discussed. The document concludes with a discussion of database modification operations like deletion, insertion and updating.

1. CS501: DATABASE AND DATA
MINING
Relational Algebra1

2. QUERY LANGUAGES
 Language in which user requests informationg g q
from the database.
 Categories of languages
 Procedural
 Non-procedural, or declarative
 “Pure” languages: Pure languages:
 Relational algebra (Procedural)
 Tuple relational calculus (Non-procedural)
 Domain relational calculus (Non-procedural)
 Pure languages form underlying basis of query
languages that people uselanguages that people use. 2

3. RELATIONAL ALGEBRA
 Procedural languageg g
 Six basic operators
 Selection: 
 Projection: 
 Union: 
 Set difference: – Set difference: –
 Cartesian product: x
 Rename: 
 The operators take one or two relations as inputs
and produce a new relation as a result.
3

4. SELECTION OPERATION
 Relation r A B C D




1
5
7
7




12
23
3
10 )()5()( rDBA 
A B C D




1
23
7
10
4

5. PROJECTION OPERATION
 Relation r
A B C



10
20
30
1
1
1
A C A C
)(, rCA


30
40
1
2 

1
1 =


1
1


1
2
 2
5

6. UNION OPERATION
 Relations r,s,
A B
1


1
2
1 A B
A B
r


1
2
sr 


2
3


1
3
6
s

7. SET DIFFERENCE OPERATION
 Relations r,s,
A B



1
2
1
A B
sr  1
A B
r


1
1
A B


2
3
7
 3
s

8. CARTESIAN PRODUCT OPERATION
 Relations r,s,
A B
1
A B C D E


1
2
r



1
1
1
1



10
10
20
10
a
a
b
b
sr 
C D
 10
E
a




1
2
2
2




10
10
10
20
b
a
a
b



10
20
10
a
b
b

 2

 10 b
8s

9. RENAME OPERATION
 Allows us to name, and therefore to refer to, the
results of relational-algebra expressions.
 Allows us to refer to a relation by more than one
name.
 Example:
 x (E)
returns the expression E under the name x
 If a relational-algebra expression E has arity n, then
returns the result of expression E under the name x,
)(),...,,( 21
EnAAAx
p ,
and with the attributes renamed to A1 , A2 , …., An . 9

10. BANKING EXAMPLE
branch (branch_name, branch_city, assets)
customer (customer_name, customer_street,
customer_city)
account (account_number, branch_name, balance)
loan (loan number branch name amount)loan (loan_number, branch_name, amount)
depositor (customer_name, account_number)
borrower (customer_name, loan_number)
10

11. BANK EXAMPLE
11

12. EXAMPLE QUERIES
 Find all loans of over Rs 2000
 Find the loan number for each loan of an amount
h R 2000
)(2000 loanamount
greater than Rs 2000
 Find the names of all customers who have a loan
))(( 2000_ loanamountnoloan 
 Find the names of all customers who have a loan,
an account, or both, from the bank
)()( borrowerdepositor namecustomernamecustomer   )()( __ p namecustomernamecustomer
12

13. EXAMPLE QUERIES
 Find the names of all customers who have a loan
at the Patliputra branch.
))(( )( loanborrowernoloanloannoloanborrowernamecustomer 
Fi d th f ll t h h l
))((
).(
)_._.(_
Patliputrabranchloan
noloanloannoloanborrowernamecustomer


 Find the names of all customers who have a loan
at the Patliputra branch but do not have an
account at any branch of the bank.
)(
))((
).(
)_._.(_
d i
loanborrower
Patliputrabranchloan
noloanloannoloanborrowernamecustomer  


13)(_ depositornamecustomer

14. SOME OTHER OPERATIONS
 Additional Operations Additional Operations
 Set intersection
 Natural join
 Outer Join
 Division
Th b ti b d i The above operations can be expressed using
basic operations we have seen earlier
14

15. SET INTERSECTION OPERATION
 Relations r,s,
A B
 2
A B
 1
 3
s


2
1
r
A B
 2
r ∩ s
15

16. SET INTERSECTION OPERATION (CONTD.)
 Set intersection operation can be built usingp g
other basic operations
 How?
r∩s=r-(r-s)
16

17. NATURAL JOIN OPERATION
 Cartesian product often requires a selectionp q
operation
 The selection operation most often requires that
ll tt ib t th t t th l tiall attributes that are common to the relations
are involved in the Cartesian product be equated
 Steps for natural join Steps for natural join
1. Perform the Cartesian product of its two arguments
2. Perform a selection forcing equality on those
tt ib t th t i b th l ti l hattributes that appear in both relational schemas
3. Finally remove the duplicate attributes
17

18. NATURAL JOIN OPERATION
 Relations r,s,
A B
 1
C

B
1
D
a
E




1
4
4
1




1
3
1
2
a
a
a
b




r s
 2  3 b 
r s
A B C D EA B



1
1
1
C D



a
a
a
E





1
1
2



a
a
b



18

19. NATURAL JOIN OPERATION (CONTD.)
 A natural join operation can be rewritten asj p
))(( ......... 2211
srnn AsArAsArAsArSR   r s
 Theta join is a variant of natural join
It i d fi d It is defined as
)( sr  r θs
19

20. ASSIGNMENT OPERATION
 It is convenient at times to write relational
algebra expression by assigning parts of it to
temporary relation variables
Th i t ti k lik i t The assignment operation works like assignment
in programming languages
 We can rewrite asr s We can rewrite as
temp1← r х s
))1(......... 2211
tempnn AsArAsArAsAr temp2←
)2(tempsrresult←
20

21. OUTER JOIN OPERATION
 An extension of the join operation that avoidsj p
loss of information
 Computes the join and then adds tuples form one
l ti th t d t t h t l i th threlation that does not match tuples in the other
relation to the result of the join.
 Uses null values: Uses null values:
 null signifies that the value is unknown or does not
exist
 All comparisons involving null are false by definition All comparisons involving null are false by definition.
21

22. DIFFERENT FORMS OF OUTER JOIN
 Left outer joinj
 Includes the tuples from the left relation that did not
match with any tuples in the right relation
 Pads the tuples with null values for all other Pads the tuples with null values for all other
attributes from the right relation
 Adds them to the result of the natural join
 Similarly we can define-
 Right outer join
F ll t j i Full outer join
 We can rewrite asr s
r s U (r-πR(r s)) x {(null, …, null)}
22
( R( )) {( , , )}
Here the constant relation {(null,…,null)} is on schema S-R

23. NULL VALUE
 It is possible for tuples to have a null value,p p ,
denoted by null, for some of their attributes
 null signifies an unknown value or that a value
does not exist.
 The result of any arithmetic expression involving
ll i llnull is null.
 Aggregate functions simply ignore null values (as
in SQL)in SQL)
 For duplicate elimination and grouping, null is
treated like any other value, and two nulls aret eated e a y ot e va ue, a d two u s a e
assumed to be the same (as in SQL)
23

24. DIVISION OPERATION
 Notation: r÷s
 Suited to queries that include the phrase “for all”.
 Let r and s be relations on schemas R and S respectively
wherewhere
 R = (A1, …, Am , B1, …, Bn )
 S = (B1, …, Bn)
The result of r  s is a relation on schema
R – S = (A1, …, Am)
{  ( ) ( ) }r  s = { t | t   R-S (r)   u  s ( tu  r ) }
Where tu means the concatenation of tuples t and u to
produce a single tupleproduce a single tuple 24

25. DIVISION OPERATION (CONTD.)
 Relations r,s,
B
A B
1
2




1
2
3
1
A




1
1
1
3
s


r÷s




4
6
1
2
r s
 2
r
25

26. DIVISION OPERATION (CONTD.)
 Definition in terms of the basic algebra operationg p
Let r(R) and s(S) be relations, and let S  R
 ( )  ( (  ( ) )  ( ))r  s = R-S (r ) – R-S ( ( R-S (r ) x s ) – R-S,S(r ))
26

27. BANK EXAMPLE
27

28. EXAMPLE QUERIES
 Find the names of all customers who have a loan
and an account at bank.
customer_name (borrower)  customer_name (depositor)
Fi d h f ll h h l Find the name of all customers who have a loan
at the bank and the loan amount
 customer name loan number amount (borrower loan)customer_name, loan_number, amount ( )
28

29. EXAMPLE QUERIES (CONTD.)
 Find the largest account balance in the bankg
 balance (account) – account.balance ( σaccount.balance <d.balance
(account x ρd account))
29

30. EXAMPLE QUERIES (CONTD.)
 Find the name of customers who have an account at
all the branches located in “Patna” city.
customer_name,branch_name (depositor account)
 branch_name (σbranch_city=“Patna” (branch))
30

31. FEW MORE JOIN OPERATIONS
 Semi joinj
 The left semi-join is similar to the natural join
 The result of this semi-join is the set of all tuples
in r for which there is a tuple in s that is equal onin r for which there is a tuple in s that is equal on
their common attribute names
 r semiJoin s = ΠA1,…, An(r naturalJoin s) where R =
{A1 A }{A1,…,An}
 Anti join
 It is similar to the natural join,s s a o e a a jo ,
 but the result of an anti-join is only those tuples
in r for which there is no tuple in s that is equal on
their common attribute namestheir common attribute names
 r antiJoin s = r – (r semiJoin s)
31

32. EXTENDED RELATIONAL ALGEBRA
OPERATIONS
 Provide the ability to write queries that cannoty q
be expressed using basic relational algebra
operations
G li d P j ti Generalized Projections
 Aggregation
32

33. GENERALIZED PROJECTION
 An extension of projection which allowsp j
operations such as arithmetic and string
functions to be used in the projection list
Π (E) ΠF1,F2,…,Fn(E)
 here F1,F2, …, Fn is an arithmetic expression
involving constants and attributes in the schema of E
 Example: ΠID,name,dept_name,salary/12(emp)
 Example: ΠID,(limit-balance) as credit_available(credit_info)
33

34. AGGREGATION
 Aggregate functions take a collection of valuesgg g
and return a single value in result
 E.g. sum, avg, count, max, min, etc.
M l i h ll i hi h Multisets: the collections on which aggregate
function operates can have multiple occurrences
of a value; the order in which the values appear; pp
is not relevant
 g sum(salary)(instructor)
Caligraphic G
34

35. MODIFICATION OF THE DATABASE
 The content of the database may be modifiedy
using the following operations:
 Deletion
 Insertion
 Updating
 All th ti d i th All these operations are expressed using the
assignment operator.
35

36. DELETION
 A delete request is expressed similarly to aq p y
query, except instead of displaying tuples to the
user, the selected tuples are removed from the
databasedatabase.
 Can delete only whole tuples; cannot delete
values on only particular attributes
 A deletion is expressed in relational algebra by:
r  r – E
where r is a relation and E is a relational algebra
query.
36

37. BANK EXAMPLE
37

38. DELETE EXAMPLE
 Delete all account records in the “Patliputra” branch.p
 r1  branch_name=“Patliputra” (account depositor)
 account  account –  account_number, branch_name, balance (r1 )
d i d i  ( 1 ) depositor  depositor -  customer_name,account_number (r1 )
 Delete all loan records with amount in the range of 0 to 50 Delete all loan records with amount in the range of 0 to 50
 r2  amount>=0 and amount <= 50 (loan borrower)
 loan  loan – loan no branch name amount (r2)loan_no,branch_name,amount ( )
 borrower  borrower – customer_name,loan_no (r2)
38

39.  Delete all accounts at branches located in cityy
‘Gaya’
r1  branch_city = “Gaya” (account branch )
r2   account_number, branch_name, balance (r1)
r3   customer_name, account_number (r2 depositor)
account  account – r2
depositor  depositor – r3
39

40. INSERTION
 To insert data into a relation, we either:,
 specify a tuple to be inserted or
 write a query whose result is a set of tuples to
be inserted
 In relational algebra, an insertion is expressed
by:by:
r  r  E
where r is a relation and E is a relational algebrag
expression.
 The insertion of a single tuple is expressed by
l tti E b t t l ti t i iletting E be a constant relation containing one
tuple.
40

41. INSERT EXAMPLE
 Insert information in the database specifying that
Sumit has Rs 1200 in account A-973 at the Patliputra
branch.
account  account  {(“A-973”, “Patliputra”, 1200)}{( , p , )}
depositor  depositor  {(“Sumit”, “A-973”)}
 Provide as a gift for all loan customers in the
Patliputra branch a Rs 200 savings account Let thePatliputra branch, a Rs 200 savings account. Let the
loan number serve as the account number for the new
savings account.
 ( (b l ))r1  (branch_name = “Patliputra” (borrower loan))
r2  (loan_number, branch_name, (r1))
account  account  (r2 x {(200)})( 2 {( )})
depositor  depositor  customer_name, loan_number (r1)
41

42. UPDATING
 A mechanism to change a value in a tupleg p
without changing all values in the tuple
 Use the generalized projection operator to do this
t ktask
r←ΠF1,F2,…,Fi(r)
Each F is eitherEach Fi is either
 the ith attribute of r, if the ith attribute is not
updated, or,
 if the attribute is to be updated Fi is an
expression, involving only constants and the
attributes of r which gives the new value forattributes of r, which gives the new value for
the attribute
42

43. UPDATE EXAMPLE
 Make interest payments by increasing allp y y g
balances by 5 percent.
 account   account_number, branch_name, balance * 1.05
(account)(account)
 Pay all accounts with balances over Rs1,00,000 a
six percent interest and pay all others five
percent
 account   account_number, branch_name, balance *
( (account ))1.06 ( balance  100000 (account ))
  account_number, branch_name, balance *
1.05 ( balance 100000 (account))
43