Regulation Analysis using RBMs
β’
0 likesβ’17 views
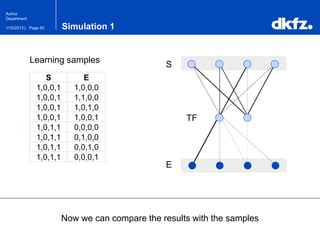
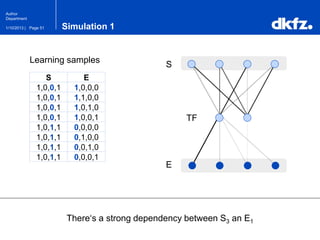
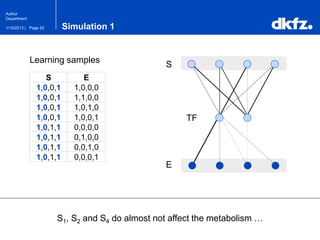
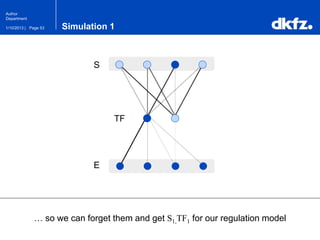
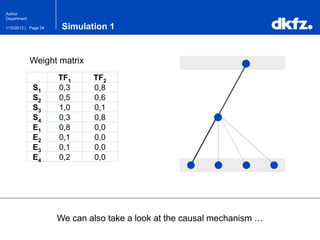
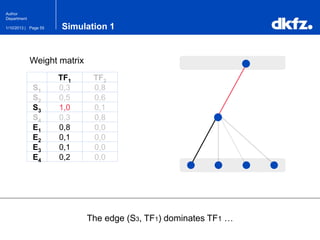
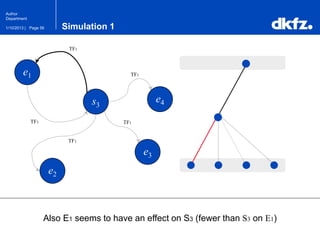
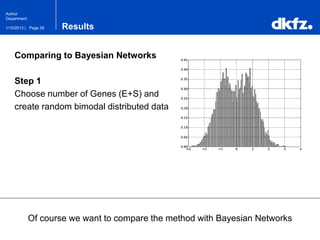
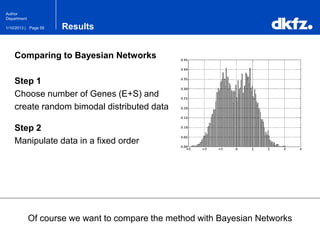
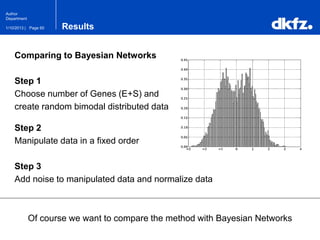
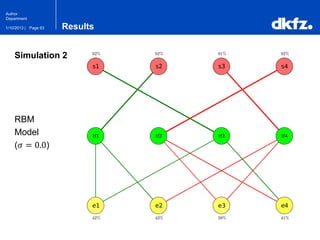
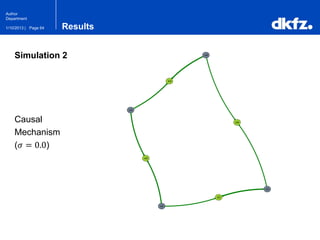
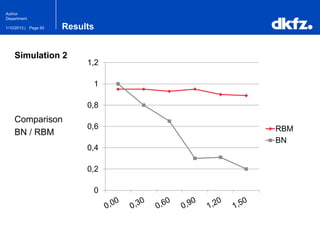
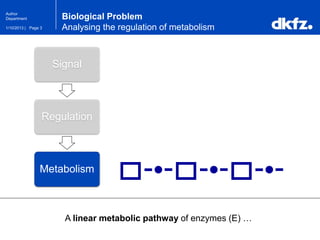
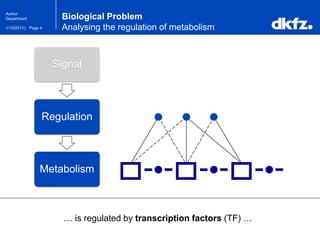
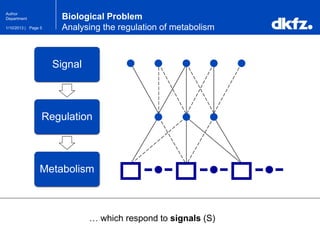
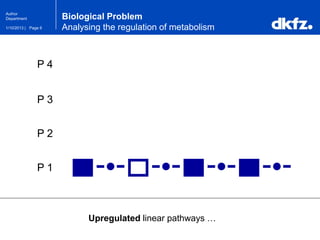
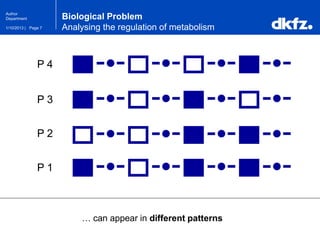
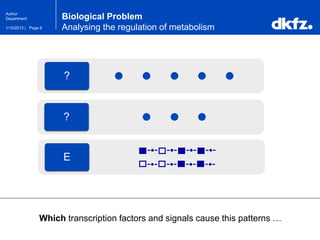
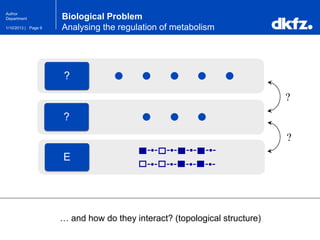
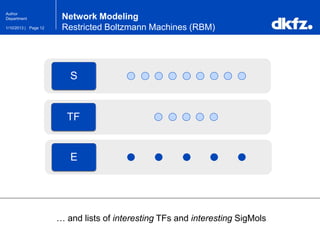
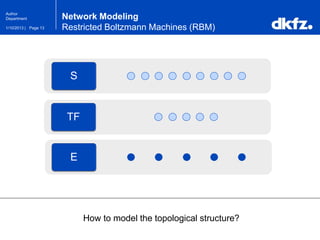
This document summarizes a presentation on using restricted Boltzmann machines to model the regulation of metabolism. It discusses using RBMs as a graphical model to represent topological network structures and preserve dependencies between transcription factors, signals, and enzymes in metabolic pathways. The document outlines how an RBM represents the network as visible and hidden units, learns the dependencies through an energy-based model and stochastic gradient descent, and validates the results on simulated data representing simple regulatory relationships.
Recommended
Recommended
More Related Content
What's hot
What's hot (19)
Similar to Regulation Analysis using RBMs
Similar to Regulation Analysis using RBMs (20)
More from Patrick Michl
More from Patrick Michl (9)
Recently uploaded
Recently uploaded (20)
Regulation Analysis using RBMs
- 1. Regulation Analysis using Restricted Boltzmann Machines Network Modeling Seminar, 10/1/2013 Patrick Michl
- 2. Page 21/10/2013 | Author Department Agenda Biological Problem Analysing the regulation of metabolism Modeling Implementation & Results
- 3. Page 31/10/2013 | Author Department Biological Problem Analysing the regulation of metabolism Signal Regulation Metabolism A linear metabolic pathway of enzymes (E) β¦
- 4. Page 41/10/2013 | Author Department Biological Problem Analysing the regulation of metabolism Signal Regulation Metabolism β¦ is regulated by transcription factors (TF) β¦
- 5. Page 51/10/2013 | Author Department Biological Problem Analysing the regulation of metabolism Signal Regulation Metabolism β¦ which respond to signals (S)
- 6. Page 61/10/2013 | Author Department P 4 P 3 P 2 P 1 Biological Problem Analysing the regulation of metabolism Upregulated linear pathways β¦
- 7. Page 71/10/2013 | Author Department P 4 P 3 P 2 P 1 Biological Problem Analysing the regulation of metabolism β¦ can appear in different patterns
- 8. Page 81/10/2013 | Author Department Biological Problem Analysing the regulation of metabolism Which transcription factors and signals cause this patterns β¦ ? E ?
- 9. Page 91/10/2013 | Author Department Biological Problem Analysing the regulation of metabolism β¦ and how do they interact? (topological structure) ? E ? ? ?
- 10. Page 101/10/2013 | Author Department Agenda Biological Problem Analysing the regulation of metabolism Network Modeling Restricted Boltzmann Machines (RBM) Validation & Implementation
- 11. Page 111/10/2013 | Author Department Network Modeling Restricted Boltzmann Machines (RBM) Lets start with some pathway of our interest β¦ S E TF
- 12. Page 121/10/2013 | Author Department Network Modeling Restricted Boltzmann Machines (RBM) β¦ and lists of interesting TFs and interesting SigMols S E TF
- 13. Page 131/10/2013 | Author Department Network Modeling Restricted Boltzmann Machines (RBM) How to model the topological structure? S E TF
- 14. Page 141/10/2013 | Author Department Graphical Models Graphical Models can preserve topological structures β¦ Network Modeling Restricted Boltzmann Machines (RBM)
- 15. Page 151/10/2013 | Author Department Graphical Models Directed Graph Undirected Graph⦠⦠but there are many types of graphical models Network Modeling Restricted Boltzmann Machines (RBM)
- 16. Page 161/10/2013 | Author Department Graphical Models Directed Graph Bayesian Networks Undirected Graph⦠The most common type is the Bayesian Network (BN) ⦠Network Modeling Restricted Boltzmann Machines (RBM)
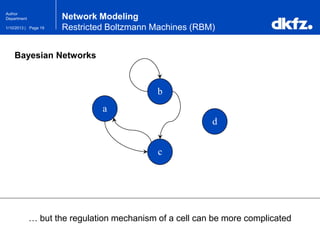
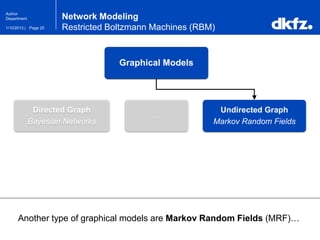
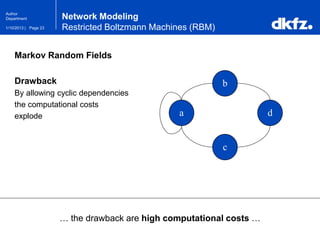
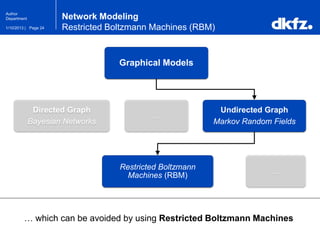
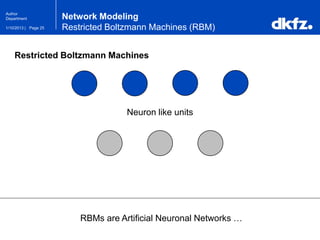
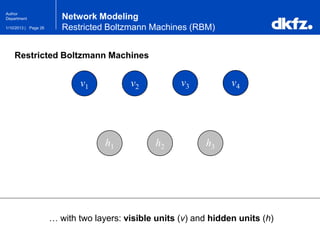
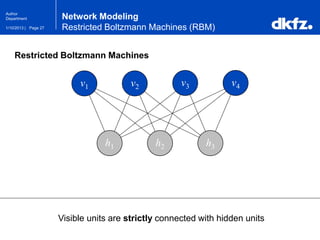
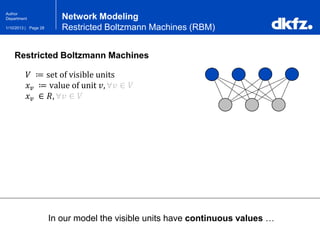
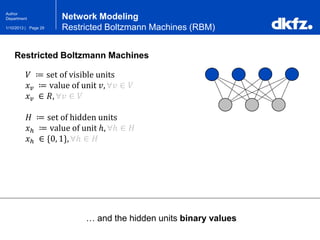
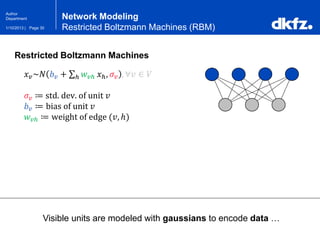
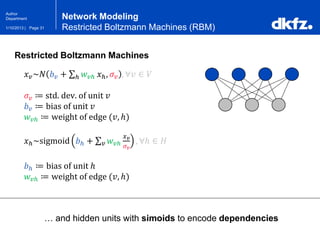
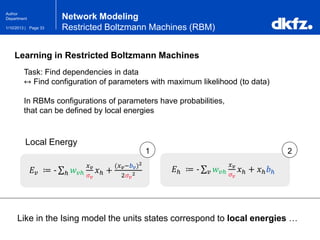
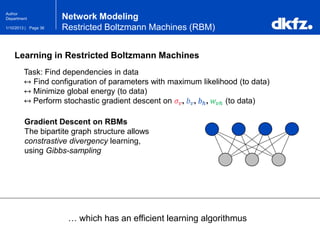
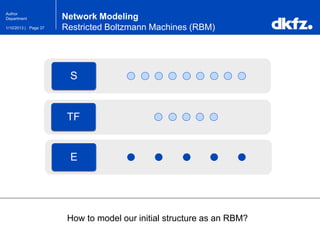
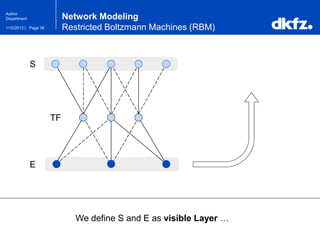
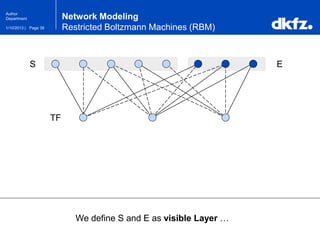
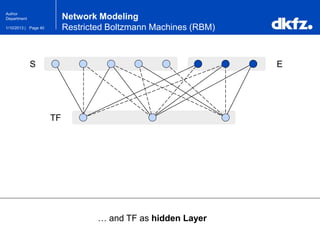
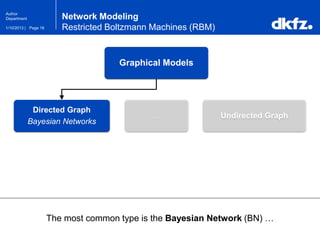
- 17. Page 171/10/2013 | Author Department Bayesian Networks Bayesian Networks use joint probabilities β¦ Network Modeling Restricted Boltzmann Machines (RBM) a b a b c P[a,b,c] 0 0 0 0.1 0 0 1 0.9 0 1 0 0.5 0 1 1 0.5 1 0 0 β¦ β¦ β¦ β¦ β¦ c ?
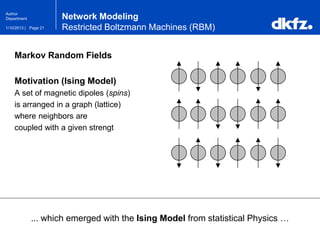
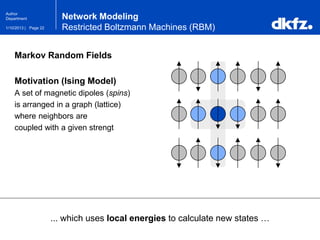
- 18. Page 181/10/2013 | Author Department Bayesian Networks β¦ to represents conditional dependencies in an acyclic graph β¦ Network Modeling Restricted Boltzmann Machines (RBM) a b a b c P[a,b,c] 0 0 0 0.1 0 0 1 0.9 0 1 0 0.5 0 1 1 0.5 1 0 0 β¦ β¦ β¦ β¦ β¦ c
- 19. Page 191/10/2013 | Author Department Bayesian Networks β¦ but the regulation mechanism of a cell can be more complicated Network Modeling Restricted Boltzmann Machines (RBM) a b c d
- 20. Page 201/10/2013 | Author Department Graphical Models Directed Graph Bayesian Networks Undirected Graph Markov Random Fields β¦ Another type of graphical models are Markov Random Fields (MRF)β¦ Network Modeling Restricted Boltzmann Machines (RBM)
- 21. Page 211/10/2013 | Author Department Markov Random Fields Motivation (Ising Model) A set of magnetic dipoles (spins) is arranged in a graph (lattice) where neighbors are coupled with a given strengt ... which emerged with the Ising Model from statistical Physics β¦ Network Modeling Restricted Boltzmann Machines (RBM)
- 22. Page 221/10/2013 | Author Department Markov Random Fields Motivation (Ising Model) A set of magnetic dipoles (spins) is arranged in a graph (lattice) where neighbors are coupled with a given strengt ... which uses local energies to calculate new states β¦ Network Modeling Restricted Boltzmann Machines (RBM)
- 23. Page 231/10/2013 | Author Department Markov Random Fields Drawback By allowing cyclic dependencies the computational costs explode β¦ the drawback are high computational costs β¦ Network Modeling Restricted Boltzmann Machines (RBM) a b c d
- 24. Page 241/10/2013 | Author Department Graphical Models Directed Graph Bayesian Networks Undirected Graph Markov Random Fields Restricted Boltzmann Machines (RBM) β¦ β¦ β¦ which can be avoided by using Restricted Boltzmann Machines Network Modeling Restricted Boltzmann Machines (RBM)
- 25. Page 251/10/2013 | Author Department RBMs are Artificial Neuronal Networks β¦ Neuron like units Network Modeling Restricted Boltzmann Machines (RBM) Restricted Boltzmann Machines
- 26. Page 261/10/2013 | Author Department β¦ with two layers: visible units (v) and hidden units (h) h1 v1 v2 v3 v4 h2 h3 Network Modeling Restricted Boltzmann Machines (RBM) Restricted Boltzmann Machines
- 27. Page 271/10/2013 | Author Department Visible units are strictly connected with hidden units h1 v1 v2 v3 v4 h2 h3 Network Modeling Restricted Boltzmann Machines (RBM) Restricted Boltzmann Machines
- 28. Page 281/10/2013 | Author Department In our model the visible units have continuous values β¦ Network Modeling Restricted Boltzmann Machines (RBM) Restricted Boltzmann Machines π β set of visible units π₯ π£ β value of unit π£, βπ£ β π π₯ π£ β π , βπ£ β π
- 29. Page 291/10/2013 | Author Department β¦ and the hidden units binary values Network Modeling Restricted Boltzmann Machines (RBM) π β set of visible units π₯ π£ β value of unit π£, βπ£ β π π₯ π£ β π , βπ£ β π π» β set of hidden units π₯β β value of unit β, ββ β π» π₯β β {0, 1}, ββ β π» Restricted Boltzmann Machines
- 30. Page 301/10/2013 | Author Department Restricted Boltzmann Machines Visible units are modeled with gaussians to encode data β¦ Network Modeling Restricted Boltzmann Machines (RBM) π₯ π£~π π π£ + π€ π£ββ π₯β, ππ£ , βπ£ β π ππ£ β std. dev. of unit π£ π π£ β bias of unit π£ π€ π£β β weight of edge (π£, β)
- 31. Page 311/10/2013 | Author Department β¦ and hidden units with simoids to encode dependencies Network Modeling Restricted Boltzmann Machines (RBM) π₯ π£~π π π£ + π€ π£ββ π₯β, ππ£ , βπ£ β π ππ£ β std. dev. of unit π£ π π£ β bias of unit π£ π€ π£β β weight of edge (π£, β) π₯β~sigmoid πβ + π€ π£βπ£ π₯ π£ π π£ , ββ β π» πβ β bias of unit β π€ π£β β weight of edge (π£, β) Restricted Boltzmann Machines
- 32. Page 321/10/2013 | Author Department The challenge is to find the configuration of the parameters β¦ Network Modeling Restricted Boltzmann Machines (RBM) Task: Find dependencies in data β Find configuration of parameters with maximum likelihood (to data) Learning in Restricted Boltzmann Machines
- 33. Page 331/10/2013 | Author Department Like in the Ising model the units states correspond to local energies β¦ Local Energy Network Modeling Restricted Boltzmann Machines (RBM) πΈβ β - π€ π£βπ£ π₯ π£ π π£ π₯β + π₯β πβπΈ π£ β - π€ π£ββ π₯ π£ π π£ π₯β + (π₯ π£βπ π£)2 2π π£ 2 Task: Find dependencies in data β Find configuration of parameters with maximum likelihood (to data) In RBMs configurations of parameters have probabilities, that can be defined by local energies 1 2 Learning in Restricted Boltzmann Machines
- 34. Page 341/10/2013 | Author Department β¦ which sum to a global energy, which is our objective function Global Energy Network Modeling Restricted Boltzmann Machines (RBM) πΈ β πΈ π£π£ + πΈββ = β π€ π£ββπ£ π₯ π£ π π£ π₯β + (π₯ π£βπ π£)2 2π π£ 2 +π£ π€ π£β π₯ π£ π π£ π₯ββ Task: Find dependencies in data β Find configuration of parameters with maximum likelihood (to data) β Minimize global energy (to data) Learning in Restricted Boltzmann Machines
- 35. Page 351/10/2013 | Author Department Learning in Restricted Boltzmann Machines The optimization can be done using stochastic gradient descent β¦ Network Modeling Restricted Boltzmann Machines (RBM) Task: Find dependencies in data β Find configuration of parameters with maximum likelihood (to data) β Minimize global energy (to data) β Perform stochastic gradient descent on ππ£, π π£, πβ, π€ π£β (to data)
- 36. Page 361/10/2013 | Author Department β¦ which has an efficient learning algorithmus Network Modeling Restricted Boltzmann Machines (RBM) Task: Find dependencies in data β Find configuration of parameters with maximum likelihood (to data) β Minimize global energy (to data) β Perform stochastic gradient descent on ππ£, π π£, πβ, π€ π£β (to data) Gradient Descent on RBMs The bipartite graph structure allows constrastive divergency learning, using Gibbs-sampling Learning in Restricted Boltzmann Machines
- 37. Page 371/10/2013 | Author Department How to model our initial structure as an RBM? Network Modeling Restricted Boltzmann Machines (RBM) S E TF
- 38. Page 381/10/2013 | Author Department We define S and E as visible Layer β¦ S E TF Network Modeling Restricted Boltzmann Machines (RBM)
- 39. Page 391/10/2013 | Author Department S E We define S and E as visible Layer β¦ TF Network Modeling Restricted Boltzmann Machines (RBM)
- 40. Page 401/10/2013 | Author Department S E β¦ and TF as hidden Layer TF Network Modeling Restricted Boltzmann Machines (RBM)
- 41. Page 411/10/2013 | Author Department Agenda Biological Problem Analysing the regulation of metabolism Network Modeling Restricted Boltzmann Machines (RBM) Implementation & Results python::metapath
- 42. Page 421/10/2013 | Author Department Results Validation of the results β’ Information about the true regulation β’ Information about the descriptive power of the data
- 43. Page 431/10/2013 | Author Department Results Validation of the results β’ Information about the true regulation β’ Information about the descriptive power of the data Without this infomation validation can only be done, using simulated data!
- 44. Page 441/10/2013 | Author Department Results Simulation 1 First of all we need to understand how the modell handles dependencies and noise To demonstrate this we create very simple data with a simple structure
- 45. Page 451/10/2013 | Author Department Simulation 1 What can we expect from this model? S E TF
- 46. Page 461/10/2013 | Author Department Simulation 1 β¦ as RBM we get 8 visible and 2 hidden units, fully connected S E TF
- 47. Page 471/10/2013 | Author Department Simulation 1 Letβs feed the machine with samples β¦ S E 1,0,0,1 1,0,0,0 1,0,0,1 1,1,0,0 1,0,0,1 1,0,1,0 1,0,0,1 1,0,0,1 1,0,1,1 0,0,0,0 1,0,1,1 0,1,0,0 1,0,1,1 0,0,1,0 1,0,1,1 0,0,0,1 Data
- 48. Page 481/10/2013 | Author Department Simulation 1 .. to get the calculated parameters (especially the weight matrix) Weight matrix TF1 TF2 S1 0,3 0,8 S2 0,5 0,6 S3 1,0 0,1 S4 0,3 0,8 E1 0,8 0,0 E2 0,1 0,0 E3 0,1 0,0 E4 0,2 0,0
- 49. Page 491/10/2013 | Author Department Simulation 1 The weights are visualized by the intensity of the edges S E TF TF1 TF2 S1 0,3 0,8 S2 0,5 0,6 S3 1,0 0,1 S4 0,3 0,8 E1 0,8 0,0 E2 0,1 0,0 E3 0,1 0,0 E4 0,2 0,0 Weight matrix
- 50. Page 501/10/2013 | Author Department Simulation 1 Now we can compare the results with the samples S E 1,0,0,1 1,0,0,0 1,0,0,1 1,1,0,0 1,0,0,1 1,0,1,0 1,0,0,1 1,0,0,1 1,0,1,1 0,0,0,0 1,0,1,1 0,1,0,0 1,0,1,1 0,0,1,0 1,0,1,1 0,0,0,1 Learning samples S E TF
- 51. Page 511/10/2013 | Author Department Simulation 1 Thereβs a strong dependency between S3 an E1 S E 1,0,0,1 1,0,0,0 1,0,0,1 1,1,0,0 1,0,0,1 1,0,1,0 1,0,0,1 1,0,0,1 1,0,1,1 0,0,0,0 1,0,1,1 0,1,0,0 1,0,1,1 0,0,1,0 1,0,1,1 0,0,0,1 Learning samples S E TF
- 52. Page 521/10/2013 | Author Department Simulation 1 S1, S2 and S4 do almost not affect the metabolism β¦ S E 1,0,0,1 1,0,0,0 1,0,0,1 1,1,0,0 1,0,0,1 1,0,1,0 1,0,0,1 1,0,0,1 1,0,1,1 0,0,0,0 1,0,1,1 0,1,0,0 1,0,1,1 0,0,1,0 1,0,1,1 0,0,0,1 Learning samples S E TF
- 53. Page 531/10/2013 | Author Department Simulation 1 β¦ so we can forget them and get S1,TF1 for our regulation model S E TF
- 54. Page 541/10/2013 | Author Department Simulation 1 We can also take a look at the causal mechanism β¦ TF1 TF2 S1 0,3 0,8 S2 0,5 0,6 S3 1,0 0,1 S4 0,3 0,8 E1 0,8 0,0 E2 0,1 0,0 E3 0,1 0,0 E4 0,2 0,0 Weight matrix
- 55. Page 551/10/2013 | Author Department Simulation 1 The edge (S3, TF1) dominates TF1 β¦ TF1 TF2 S1 0,3 0,8 S2 0,5 0,6 S3 1,0 0,1 S4 0,3 0,8 E1 0,8 0,0 E2 0,1 0,0 E3 0,1 0,0 E4 0,2 0,0 Weight matrix
- 56. Page 561/10/2013 | Author Department Simulation 1 Also E1 seems to have an effect on S3 (fewer than S3 on E1) s3 e1 e2 e3 e4 TF1 TF1 TF1 TF1 TF1
- 57. Page 571/10/2013 | Author Department Results Comparing to Bayesian Networks For this purpose we simulate data in three steps Of course we want to compare the method with Bayesian Networks
- 58. Page 581/10/2013 | Author Department Results Comparing to Bayesian Networks Step 1 Choose number of Genes (E+S) and create random bimodal distributed data Of course we want to compare the method with Bayesian Networks
- 59. Page 591/10/2013 | Author Department Results Comparing to Bayesian Networks Step 1 Choose number of Genes (E+S) and create random bimodal distributed data Step 2 Manipulate data in a fixed order Of course we want to compare the method with Bayesian Networks
- 60. Page 601/10/2013 | Author Department Results Comparing to Bayesian Networks Step 1 Choose number of Genes (E+S) and create random bimodal distributed data Step 2 Manipulate data in a fixed order Step 3 Add noise to manipulated data and normalize data Of course we want to compare the method with Bayesian Networks
- 61. Page 611/10/2013 | Author Department Results Comparing to Bayesian Networks Idea β’ βmelt downβ the bimodal distribution from very sharp to very noisy β’ Try to find the original causal structure with BN and RBM β’ Measure Accuracy by counting the right and wrong dependencies Of course we want to compare the method with Bayesian Networks
- 62. Page 621/10/2013 | Author Department Simulation 2 Results π1 = 0.5π 1 + 0.5π 2 + π(π = 0, π) π2 = 0.5π 2 + 0.5π 3 + π(π = 0, π) π3 = 0.5π 3 + 0.5π 4 + π(π = 0, π) π4 = 0.5π 4 + 0.5π 1 + π(π = 0, π) Of course we want to compare the method with Bayesian Networks Step 1: Number of visible nodes 8 (4E, 4S) Create intergradient datasets from sharp to noisy bimodal distribution π1 = 0.0, π1 = 0.3, π3 = 0.9, π4 = 1.2, π4 = 1.5 Step 2 + 3: Data Manipulation + add noise
- 63. Page 631/10/2013 | Author Department Results Simulation 2 RBM Model (π = 0.0)
- 64. Page 641/10/2013 | Author Department Results Simulation 2 Causal Mechanism (π = 0.0)
- 65. Page 651/10/2013 | Author Department Results Simulation 2 Comparison BN / RBM 0 0,2 0,4 0,6 0,8 1 1,2 RBM BN
- 66. Page 661/10/2013 | Author Department Conclusion Conclusion β’ RBMs are more stable against noise compared to BNs. It has to be assumed that RBMs have high predictive power regarding the regulation mechanisms of cells β’ The drawback are high computational costs Since RBMs are getting more popular (Face recognition / Voice recognition, Image transformation). Many new improvements in facing the computational costs have been made.
- 67. Page 671/10/2013 | Author Department Acknowledgement eilsLABS PD Dr. Rainer KΓΆnig Prof. Dr Roland Eils Network Modeling Group