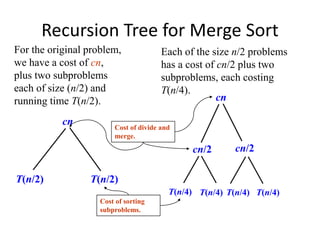
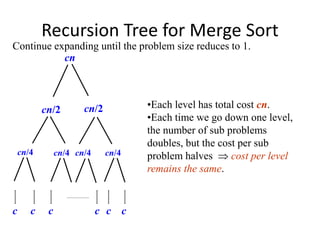
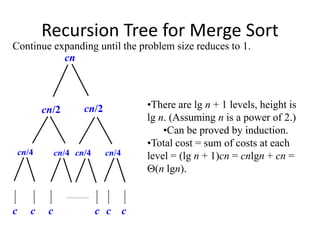
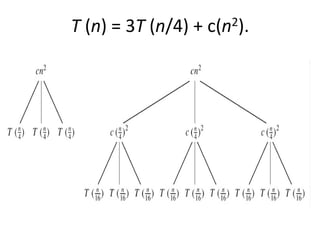
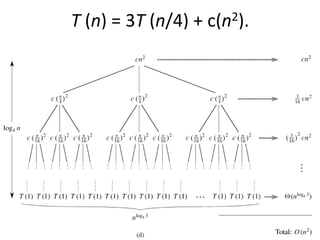
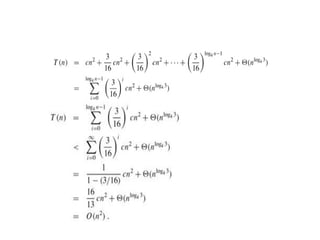The document discusses using recursion trees to analyze divide and conquer algorithms. It provides an example of using a recursion tree to solve the recurrence relation for merge sort. The recursion tree shows the successive divisions of the problem into smaller subproblems until the base case is reached. Each node represents the cost of a subproblem, and the total cost is calculated by summing the costs at each level of the tree. For merge sort, the tree has log n levels, with a total cost of O(n log n).

1. Design and Analysis of Algorithms
Recurrence Relations
The Recursion Tree Method

2. Recursion Tree Method
• It is difficult to come up with good guess.
• Example of merge sort.
• In recursion tree
– Each node represents cost of single sub-problem
– We sum the cost with in each level of tree
– We sum all such level costs.
• Useful when the recurrence describes the running
time of divide and conquer algorithm.

3. • Use recursion trees to devise good guesses.
• Recursion Trees
– Show successive expansions of recurrences using
trees.
– Keep track of the time spent on the sub problems
of a divide and conquer algorithm.
– Help organize the algebraic bookkeeping
necessary to solve a recurrence.
Recursion Tree Method

4. Recursion Tree – Example
• Running time of Merge Sort:
T(n) = (1) if n = 1
T(n) = 2T(n/2) + (n) if n > 1
• Rewrite the recurrence as
T(n) = c if n = 1
T(n) = 2T(n/2) + cn if n > 1
c > 0: Running time for the base case and
time per array element for the divide and
combine steps.

5. Recursion Tree for Merge Sort
For the original problem,
we have a cost of cn,
plus two subproblems
each of size (n/2) and
running time T(n/2).
cn
T(n/2) T(n/2)
Each of the size n/2 problems
has a cost of cn/2 plus two
subproblems, each costing
T(n/4).
cn
cn/2 cn/2
T(n/4) T(n/4) T(n/4) T(n/4)
Cost of divide and
merge.
Cost of sorting
subproblems.

6. Recursion Tree for Merge Sort
Continue expanding until the problem size reduces to 1.
cn
cn/2 cn/2
cn/4 cn/4 cn/4 cn/4
c c c c
c c
lg n
cn
cn
cn
cn
Total : cnlgn+cn

7. Recursion Tree for Merge Sort
Continue expanding until the problem size reduces to 1.
cn
cn/2 cn/2
cn/4 cn/4 cn/4 cn/4
c c c c
c c
•Each level has total cost cn.
•Each time we go down one level,
the number of sub problems
doubles, but the cost per sub
problem halves  cost per level
remains the same.

8. Recursion Tree for Merge Sort
Continue expanding until the problem size reduces to 1.
cn
cn/2 cn/2
cn/4 cn/4 cn/4 cn/4
c c c c
c c
•There are lg n + 1 levels, height is
lg n. (Assuming n is a power of 2.)
•Can be proved by induction.
•Total cost = sum of costs at each
level = (lg n + 1)cn = cnlgn + cn =
(n lgn).

9. • Best used to generate good guess.
• Verified using substitution method.
• For example T (n) = 3T (n/4) + (n2).
• Rewrite it
– T (n) = 3T (n/4) + cn2.
• We assume that n is an exact power of 4
Recursion Tree Method

10. T (n) = 3T (n/4) + c(n2).

11. T (n) = 3T (n/4) + c(n2).

12. T (n) = 3T (n/4) + c(n2).
• Sub problem sizes decrease as we get further from
the root
• We eventually must reach a boundary condition.
• How far from the root do we reach one?

13. T (n) = 3T (n/4) + c(n2).
• The sub problem size for a node at depth i is n/4i.
• Thus, the sub problem size hits n = 1
when n/4i = 1 or
equivalently, when i = log4 n.
• Thus, the tree has log4n + 1 levels (0, 1, 2,..., log4n).

14. • Each level has three times more nodes than the level
above
• So the number of nodes at depth i is 3i.
• Because sub problem sizes reduce by a factor of 4 for
each level we go down from the root.
• Each node at depth i, for i = 0, 1, 2,..., log4 n - 1, has a
cost of c(n/4i)2.
T (n) = 3T (n/4) + c(n2).

15. • Multiplying, we see that the total cost over all nodes
at depth i, for i = 0, 1, 2,..., log4 n - 1, is
3i c(n/4i)2 = (3/16)i cn2
• The last level, at depth log4 n, has 3log
4
n =nlog
4
3nodes,
each contributing cost T (1).
• Total Cost is nlog
4
3T(1), which is
(nlog
4
3T(1))
T (n) = 3T (n/4) + c(n2).