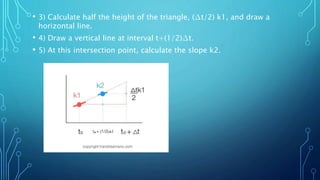
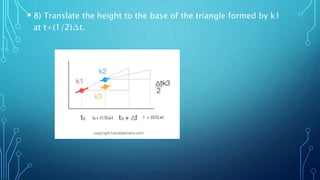
The Runge-Kutta method is a numerical integration technique providing improved approximations to motion equations by calculating multiple slopes and using them as weighted averages, unlike Euler's method which only considers a single slope. The method involves a series of steps to derive slopes k1, k2, k3, and k4 to generate a more accurate value for the object's position and velocity. The document aims to visually explain the computation process of the Runge-Kutta method.

2. WHY RK METHOD ?
• The Runge-Kutta Method is a numerical integration technique
which provides a better approximation to the equation of
motion. Unlike the Euler's Method, which calculates one slope
at an interval, the Runge-Kutta calculates four different slopes
and uses them as weighted averages.

3. • 1) At time interval t0, calculate slope k1.
• 2) Create a triangle by projecting k1 to t+∆t.

4. • 3) Calculate half the height of the triangle, (∆t/2) k1, and draw a
horizontal line.
• 4) Draw a vertical line at interval t+(1/2)∆t.
• 5) At this intersection point, calculate the slope k2.

5. • 6) Starting out with k2, create a triangle by projecting k2 to
t+(3/2)∆t.
• 7) Calculate half the height of the triangle, (∆t/2)k2.

6. • 8) Translate the height to the base of the triangle formed by k1
at t+(1/2)∆t.

7. • 10) Create the another triangle by projecting k3 to t+(3/2)∆t
• 11) Find half the height of the triangle, (∆t/2)k3

8. • 13) Find the slope k4.

9. THE RUNGA-KUTTA USES THESE SLOPES AS WEIGHTED AVERAGE TO
BETTER APPROXIMATE THE ACTUAL SLOPE, VELOCITY, OF THE
OBJECT. THE POSITION OF THE OBJECT IS THEN CALCULATED USING
THIS NEW SLOPE.

10. • I hope this visual depiction of the Runge-Kutta method helps.