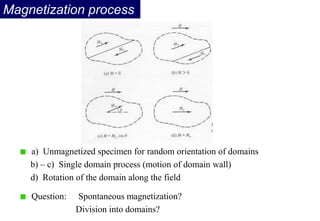
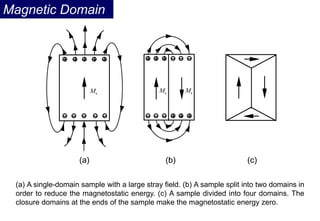
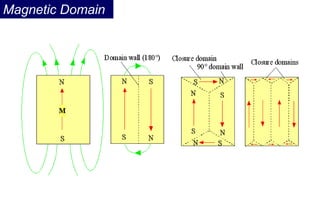
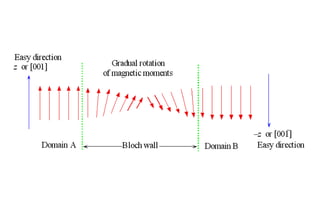
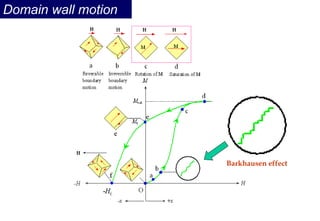
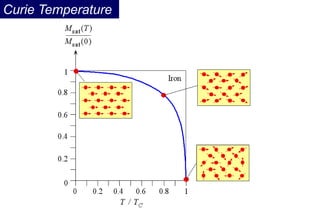
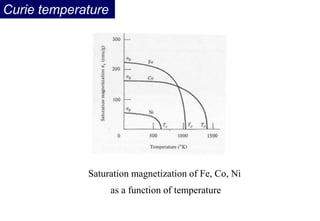
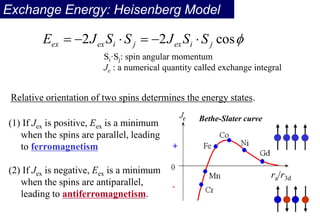
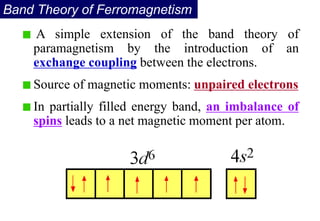
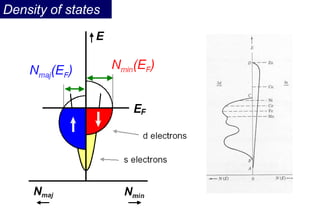
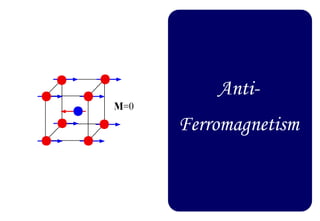
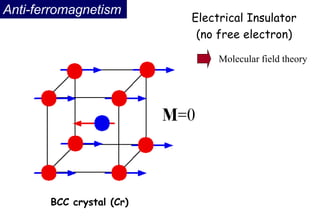
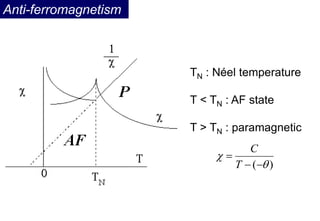
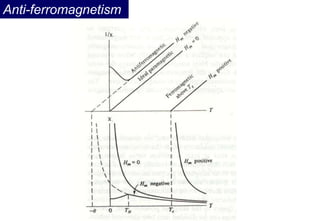
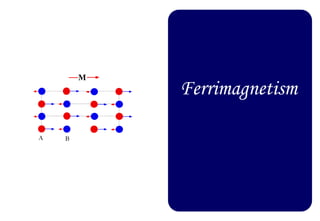
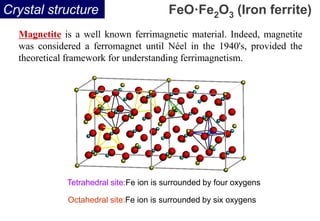
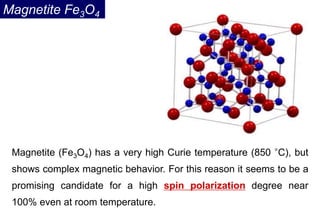
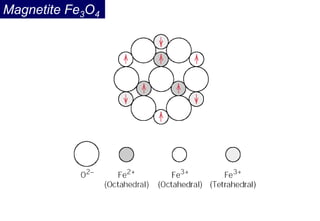
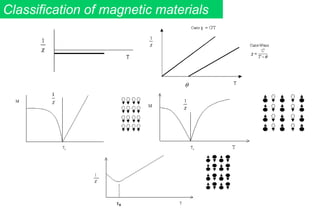
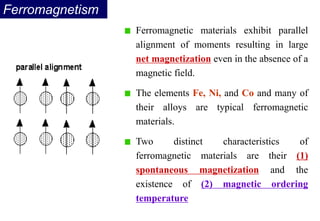
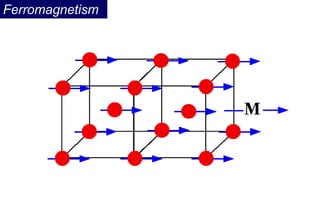
Ferromagnetism arises from the parallel alignment of atomic magnetic moments due to strong exchange interactions between electrons. Ferromagnetic materials can exhibit spontaneous magnetization and magnetic ordering temperatures. The exchange force is a quantum mechanical phenomenon that favors parallel spin alignment of electrons and results in large internal molecular fields that align atomic moments. Ferrimagnetism is a similar phenomenon where sublattices have unequal and opposing magnetic moments, resulting in a net magnetic moment. Common ferrimagnetic materials include ferrites with spinel and hexagonal structures.

1. Ferromagnetism

2. Ferromagnetism
The atomic moments in these materials exhibit very
strong interactions, resulting in a parallel or
antiparallel alignment of atomic moments.
Exchange forces are very large, equivalent to a field
on the order of 1000 Tesla, or approximately a 100
million times the strength of the earth's field.
The exchange force is a quantum mechanical
phenomenon due to the relative orientation of the
spins of two electron.

3. Ferromagnetism
Ferromagnetic materials exhibit parallel
alignment of moments resulting in large
net magnetization even in the absence of a
magnetic field.
The elements Fe, Ni, and Co and many of
their alloys are typical ferromagnetic
materials.
Two distinct characteristics of
ferromagnetic materials are their (1)
spontaneous magnetization and the
existence of (2) magnetic ordering
temperature

4. Ferromagnetism

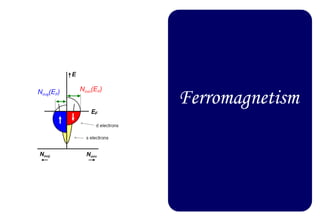
5. Hund’s rule
Fe: [Ar]3d64s2
Origin of Ferromagnetism

6. Ferromagnetism
Ferromagnetic transition metals: Fe, Co, Ni
i) Magnitude of Ms
ii) Way to reach Ms
M (ferro) >> M (para) : 1700 emu/cm3 for Fe >> 10-3 emu/cm3
Hs = 50 Oe

7. Weiss' Assumption
Molecular field is acting in FM not only above Tc
but also below Tc and this field is so strong that it
could magnetize the substance to saturation even in
the absence of an applied field. → spontaneously
magnetized (Self-saturating)
Magnetic domain : In demagnetized state, a
ferromagnetic material is divided into a number of
small regions called domains, each of which is
spontaneously magnetized.

8. Magnetization process
a) Unmagnetized specimen for random orientation of domains
b) – c) Single domain process (motion of domain wall)
d) Rotation of the domain along the field
Question: Spontaneous magnetization?
Division into domains?

9. Ms Ms Ms
(a) (b) (c)
Ms Ms Ms
(a) (b) (c)
(a) A single-domain sample with a large stray field. (b) A sample split into two domains in
order to reduce the magnetostatic energy. (c) A sample divided into four domains. The
closure domains at the ends of the sample make the magnetostatic energy zero.
Magnetic Domain

10. Magnetic Domain

12. Domain wall motion
Barkhausen effect

13. Magnetic Order
Are ferromagnets already in
an ordered state before a
magnetic field is applied or is
the order by the field?

14. Explanation of magnetic order in ferromagnets
Weber (1852): The material could already have
small atomic magnetic moments within the solid
which are randomly aligned in the demagnetized but
which became ordered under the action of a magnetic
field.
Poisson (1983) : The atomic magnetic moments may
not exist at all in the demagnetized state but could be
induced by a mangetic field.

15. Explanation of magnetic order in ferromagnets
• Ampère (1827): The origin of the atomic moments
was suggested that they were due to electrical
currents continually circulating within the atom.
• Ewing (1893): Followed Weber’s idea and interested
in explaining hysteresis.

16. Atomic magnetic moments were in permanent
existence (Weber’s hypothesis)
Atomic magnetic moments were ordered even in the
demagnetized state. It was the domains only which
were randomly aligned in the demagnetized state.
The magnetization process consisting of reorienting
the domains so that more domains were aligned with
field.
Weiss domain theory

17. Magnetic Domain
In order to minimize its magnetostatic energy, the
magnetic material divides up into magnetic domains.
Weiss (1907): concept of magnetic domains. A
magnetic material consisted of a number of distinct
regions termed ‘domains’ each of which was saturated in
a different direction.
The concept of domains is able to explain why
ferromagnetic materials can be demagnetized even
below their Curie temperature.

18. What is the origin of the alignment of the atomic
magnetic moments?
It is the Weiss mean field (later the “molecular
field”, further later exchange coupling from
quantum mechanics)
Weiss Mean Field Theory

19. Curie-Weiss Law
Curie's law: Individual carrier of magnetic moment (atoms or
molecules) do not interact with one another
Curie-Weiss law:
 Under the consideration of interaction between electrons
 Fictitious internal field Hm (“molecular field”) for interaction
: molecular field constant
M
Hm 

m
t H
H
H 

T
C
kT
n
H
M







3
2
T
C
M
H
M

 )
( 
 


C
T
CH
M












T
C
C
T
C
H
M

20. Molecular field theory
Pierre Weiss introduced molecular field concept.
Interaction between magnetic moments  Fictitious internal filed




T
C
C

 
M
Hm 

For  > 0, Hm || M
: molecular field constant
M
H
H
H
H a
m
a
tot 





21. Curie Temperature

22. Curie Temperature
Even though electronic exchange forces in ferromagnets
are very large, thermal energy eventually overcomes
the exchange and produces a randomizing effect.
This occurs at a particular temperature called the Curie
temperature (TC).
Below the Curie temperature, the ferromagnet is
ordered and above it, disordered.
The saturation magnetization goes to zero at the Curie
temperature.

23. Curie temperature
Saturation magnetization of Fe, Co, Ni
as a function of temperature

24. Exchange Energy
Exchange force depends on relative orientation of spins of two
electrons due to Pauli's exclusion principle
When two atoms, such as hydrogen atoms, are coming
together, there are electrostatic attractive (e-↔p+) and
repulsive (e-↔e-, p+↔p+) forces and exchange force.
The internal field is produced by interactions between nearest-
neighbor dipole moments.
The interaction arises from the electrostatic electron-electron
interaction, and is called the ”exchange interaction” or
exchange force.

25. Exchange Energy: Heisenberg Model
Si·Sj: spin angular momentum
Je : a numerical quantity called exchange integral

cos
2
2 j
i
ex
j
i
ex
ex S
S
J
S
S
J
E 





ra/r3d
Bethe-Slater curve
(1) If Jex is positive, Eex is a minimum
when the spins are parallel, leading
to ferromagnetism
(2) If Jex is negative, Eex is a minimum
when the spins are antiparallel,
leading to antiferromagnetism.
Relative orientation of two spins determines the energy states.

26. Band Theory of Ferromagnetism
A simple extension of the band theory of
paramagnetism by the introduction of an
exchange coupling between the electrons.
Source of magnetic moments: unpaired electrons
In partially filled energy band, an imbalance of
spins leads to a net magnetic moment per atom.

27. Band Theory
When N atoms come together
to form a solid, each level of
the free atom must split into N
levels.
In transition metal elements, the
outermost electrons are the 3d
and 4s; these electron clouds
are the first to overlap as the
atoms are brought together, and
the corresponding levels are the
first to split.

28. Density of states

30. Anti-
Ferromagnetism

31. Anti-ferromagnetism
If the A and B sublattice moments are exactly equal
but opposite, the net moment is zero. This type of
magnetic ordering is called antiferromagnetism.
The clue to antiferromagnetism is the behavior of
susceptibility above a critical temperature, called the
Néel temperature (TN).
Above TN, the susceptibility obeys the Curie-Weiss
law for paramagnets but with a negative intercept
indicating negative exchange interactions.

32. Wess Model on Anti-ferromagnetism
Two identical sublattices A and B: While the
interaction with the moments on other sublattices
with a negative coupling coefficient, interaction
with the moments on their own sublattice with a
positive coupling coefficient
On the basis of nearest-neighbor interactions,
with a negative interaction between nearest
neighbors, this leads to simple antiferromagnetism

33. Anti-ferromagnetism
BCC crystal (Cr)
Electrical Insulator
(no free electron)
Molecular field theory

34. Anti-ferromagnetism
TN : Néel temperature
T < TN : AF state
T > TN : paramagnetic
)
( 




T
C

35. Anti-ferromagnetism

36. Ferrimagnetism

37. In ferrimagnets, the magnetic moments of the A and
B sublattices are not equal and result in a net
magnetic moment.
Ferrimagnetism is therefore similar to
ferromagnetism. It exhibits all the hallmarks of
ferromagnetic behavior- spontaneous magnetization,
Curie temperatures, hysteresis, and remanence.
However, ferro- and ferrimagnets have very different
magnetic ordering.
Ferrimagnetism

38. Ferrimagnetism
Two groups of ferrites depending on their structure
1. Cubic :
 General formula : MOFe2O3 where M is a divalent
metal ion (Mn, Ni, Fe, Co, Mg, ...)
 CoOFe2O3 is magnetically hard, but all the other cubic
ferrites are magnetically soft.
 magnetite : Fe3O4 = FeOFe2O3 : oldest ferrite
(lodestone, iron ferrite)
2. Hexagonal :
 Barium ferrite (BaO6Fe2O3) is magnetically hard

39. Cubic ferrites (Spinel structure)
MO·Fe2O3: M = Mn, Ni, Fe, Co, Mg, etc.
 In the unit cell, total 56 ions (8 M2+ ions, 16 Fe3+ ions, 32
O2
- ions)
64 tetrahedral A site / 8 = 8
32 octahedral B site / 2 = 16
 Normal Spinel : 8 M2+ in A, 16 Fe3+ in B
 Inverse Spinel : 8 Fe3+ in A, 8 M2+ + 8 Fe3+ in B
 Intermediate structure : Nor perfectly normal or inverse
structure
MnO · Fe2O3 (80% on A, 20% on B)
MgO · Fe2O3 (10% on A, 90% on B)
 Most commercial ferrites : a mixed ferrite like (Ni, Zn)O ·
Fe2O3

40. Hexagonal Ferrites
MO·6Fe2O3(= BaFe12O19) where M = Ba, Sr
 Calculated saturation magnetization
= 20μB/molecule (experimental)
 Other oxides
BaO·2MO·8Fe2O3 W
2(BaO·2MO·3Fe2O3) Y
3BaO·2MO·12Fe2O3) Z
where, M is a divalent ion

41. Other Ferrites
γ-Fe2O3 : tetragonal
(calculated net moment/molecule = 2.5μB
↔ 2.39μB experimental)
Garnets : 3M2O3・5Fe2O3 (M = Y or RE)
Alloys : Mn2Sb, Mn3Ga, Mn3Ge2, Mn3In, FeGe2, FeSe,
Cr3As2, CrPt3,
RECo5 (RE: Gd, Tb, Dy, Ho, Eu, or Tm)

42. Crystal structure
Tetrahedral site:Fe ion is surrounded by four oxygens
Octahedral site:Fe ion is surrounded by six oxygens
FeO·Fe2O3 (Iron ferrite)
Magnetite is a well known ferrimagnetic material. Indeed, magnetite
was considered a ferromagnet until Néel in the 1940's, provided the
theoretical framework for understanding ferrimagnetism.

43. Magnetite (Fe3O4) has a very high Curie temperature (850 °C), but
shows complex magnetic behavior. For this reason it seems to be a
promising candidate for a high spin polarization degree near
100% even at room temperature.
Magnetite Fe3O4

44. Magnetite Fe3O4

45. Differences with Ferromagnetism
Smaller s/0 than that for Fe
Curie-Weiss behavior above Tc is not obeyed (Non-linear)
NiO •Fe2O3 :
Expected to have 12 B if ferromagnetic
Experiment: 2.3 B (56 emu/g) at 0 K

46. Spontaneous magnetizations
Spontaneous magnetizations of the A and B sublattices and the resultant s

47. Kinds of Magnetism
Diamagnetism
Paramagnetism
Non-cooperative
(statistical) behavior
Ferromagnetism
Antiferromagnetism
Ferrimagnetism
Cooperative behavior

48. Classification of magnetic materials