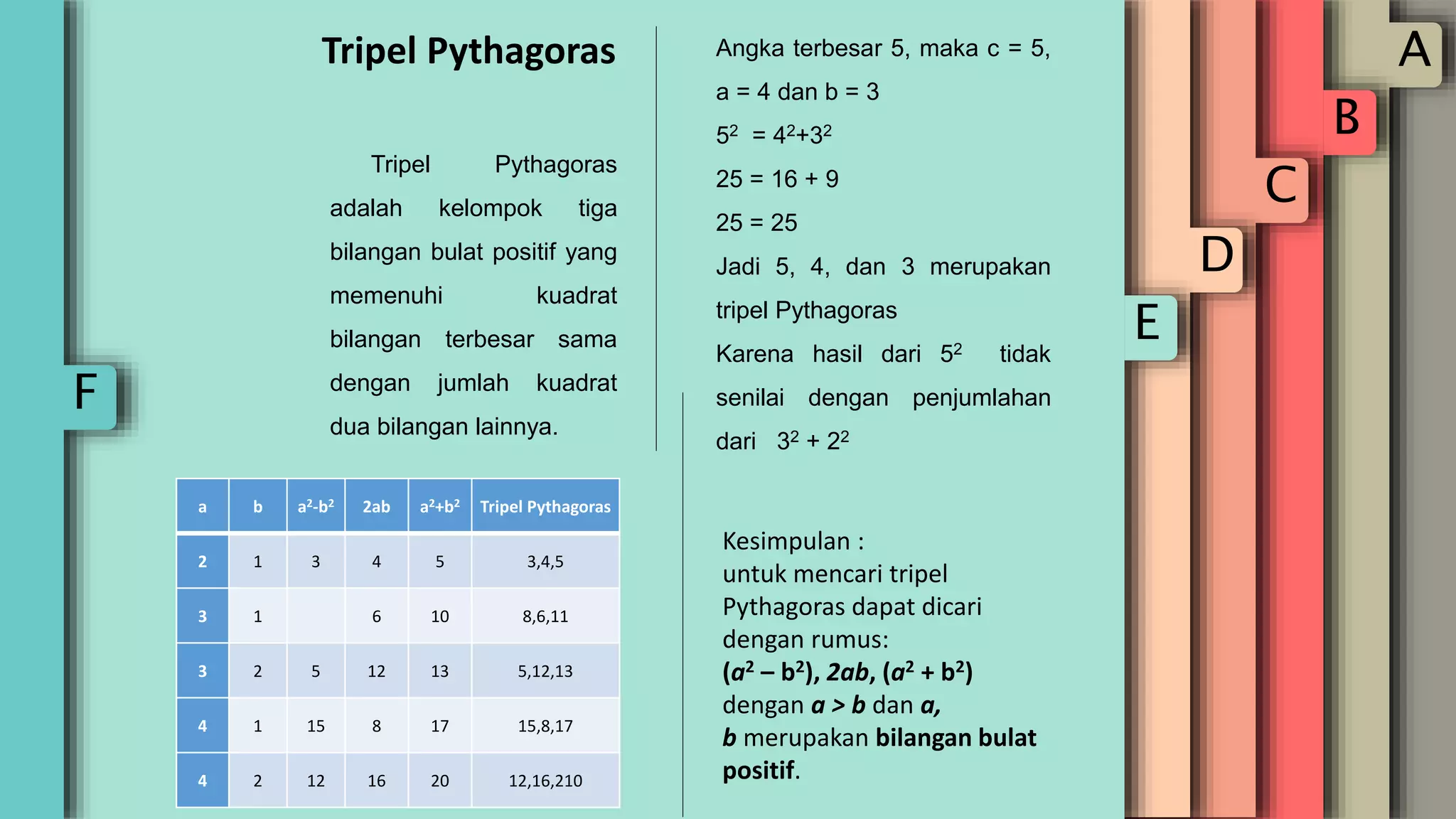
Dokumen tersebut membahas tentang matematikawan Yunani bernama Pythagoras yang dikenal karena teoremanya yaitu Teorema Pythagoras. Teorema ini menyatakan bahwa pada segitiga siku-siku, kuadrat hipotenusa sama dengan jumlah kuadrat kedua sisi lainnya. Dokumen ini juga menjelaskan berbagai cara untuk membuktikan rumus teorema Pythagoras dan contoh penerapannya dalam menyelesaikan masal

1. A
B
C
D
E
F
PYTHAGOR
ASDESIGNED BY ANNISA RAMADHANI
1705045038
. . . . . .

2. A
B
C
D
E
F
Pythagoras (582 SM - 496 SM)
adalah seorang matematikawan
dan filsuf Yunani yang paling
dikenal melalui salah satu
teoremanya, yaitu dalil
Pythagoras.
Teorema Pythagoras
berbunyi: pada suatu segitiga
siku-siku berlaku sisi miring
(hipotenusa) kuadrat sama
dengan jumlah kuadrat sisi-sisi
lainnya. Secara umum, jika
segitiga ABC siku-siku di C
maka teorema Pythagoras
dapat dinyatakan:
𝑎2 + 𝑏2 = 𝑐2
Pythagoras

3. A
B
C
D
E
F
A B
(i)
C
(ii)
Luas Persegi :
1). L (i) = AB2
2). L(ii) = AC2
3). L(iii) = BC2
Jadi :
L(i) + L(ii) = L(iii)
atau
AB2 + AC2 = BC2
Pembuktian Rumus
Pythagoras
(iii)

4. A
B
C
D
E
F
𝑎
𝑎
𝑎
𝑎𝑏
𝑏
𝑏
𝑐
𝑐
𝑐
𝑐
Dengan menghitung luas bangun bujur sangkar yang terjadi
melalui dua cara akan diperoleh:
(a + b) = c2 + 4. ½ ab
a2 + 2ab + b2 = c2 + 2 ab
a2 + b2 = c2
Pembuktian dengan diagram pythagoras
𝑏

5. A
B
C
D
E
F
a
b
c
c
b
Luas 3 segitiga
=
1
2
𝑎𝑏 +
1
2
𝑐2
+
1
2
𝑎𝑏
= 𝑎𝑏 + 𝑐2
+ 𝑎𝑏
= 2𝑎𝑏 + 𝑐2
= 𝑐2
Luas trapesium
=
1
2
𝑎 + 𝑏 𝑎 + 𝑏
= (𝑎 + 𝑏)2
= 𝑎2
+ 2𝑎𝑏 + 𝑏2
Luas trapesium = Luas 3 segitiga
𝑎2
+ 2𝑎𝑏 + 𝑏2
= 2𝑎𝑏 + 𝑐2
𝑎2
+ 𝑏2
= 𝑐2
𝑐2
= 𝑐2
Pembuktian Teorema
Pythagoras
oleh Presiden J. A.
Garfield
a

6. A
B
C
D
E
F
Tripel Pythagoras
adalah kelompok tiga
bilangan bulat positif yang
memenuhi kuadrat
bilangan terbesar sama
dengan jumlah kuadrat
dua bilangan lainnya.
Tripel Pythagoras
Kesimpulan :
untuk mencari tripel
Pythagoras dapat dicari
dengan rumus:
(a2 – b2), 2ab, (a2 + b2)
dengan a > b dan a,
b merupakan bilangan bulat
positif.
Angka terbesar 5, maka c = 5,
a = 4 dan b = 3
52 = 42+32
25 = 16 + 9
25 = 25
Jadi 5, 4, dan 3 merupakan
tripel Pythagoras
Karena hasil dari 52 tidak
senilai dengan penjumlahan
dari 32 + 22
a b a2-b2 2ab a2+b2 Tripel Pythagoras
2 1 3 4 5 3,4,5
3 1 6 10 8,6,11
3 2 5 12 13 5,12,13
4 1 15 8 17 15,8,17
4 2 12 16 20 12,16,210

7. A
B
C
D
E
F
Contoh Soal
5 cm 4 cm
?
Diketahui sebuah tangga disandarkan pada
tembok. Jika panjang tangga adalah 5 m dan
tinggi temboknya adalah 4 m, tentukan jarak
antara kaki tangga dengan temboknya!
Jawab:
Misalkan jarak antara kaki tangga dan tembok
adalah x, maka untuk menentukan nilai x dapat
digunakan Rumus Phytagoras sebagai berikut
ini.
c2 = a2 + b2
sisi miring atau c = 5m
tinggi atau b = 4m
ditanyakan alas atau x
x² = c² - b²
c² = 5² - 4²
c² = 25 - 16
c² = 9
c = 9
c = 3
Jadi, jarak antara kaki tangga dan tembok adalah 3 m.

8. A
B
C
D
E
F
Contoh Soal
Tentukan segitiga berikut
termasuk tripel Pytaoras
atau tidak jika diketahui
panjang sisi-sisinya adalah
7 cm, 24 cm, dan 25 cm !
Karena
c² = a² + b²
625 = 625
Oleh karena itu segitiga tersebut termasuk
dalam tripel segitiga.
Jawab
Misalkan c adalah sisi terpanjang dan b, a
adalah dua sisi lainnya, maka diperoleh:
c = 25 cm, b = 7 cm, a = 24 cm.
c² = 25² = 625
a² + b² = 7² + 24² = 49 + 576 = 625

9. A
B
C
D
E
F