This document discusses solving a parabolic partial differential equation (PDE) describing heat conduction using the MATLAB PDE solver. It provides an example of using the pdepe solver to find the temperature distribution in a steel rod over time, given the boundary temperatures and properties of the rod. The document includes the equations, initial and boundary conditions, and MATLAB code used to set up and solve the PDE numerically using pdepe.

1. Solving heat conduction equation
(Parabolic PDE) using
matlab PDE solver

2. Physical Example of an Parabolic PDE
The internal temperature of a metal rod exposed to two different temperatures
at each end can be found using the heat conduction equation.
t
T
x
T


=


2
2

A thin rod, insulated at all points except at its ends.
C
k

 =

3. Example
Consider a steel rod that is subjected to a temperature of on the left
end and on the right end. If the rod is of length ,use the implicit
method to find the temperature distribution in the rod from and
seconds. Use , .
Given: , ,
The initial temperature of the rod is .
C

100
C

25 m
05
.
0
0
=
t 9
=
t
m
x 01
.
0
=
 s
t 3
=

K
m
W
k
−
= 54 3
7800
m
kg
=

K
kg
J
C
−
= 490
C

20
0
=
i 1 2 3 4 5
m
01
.
0
C
T 
= 25
C
T 
=100

4. Solution
Recall,
therefore,
C
k

 =
490
7800
54

=

s
m /
10
4129
.
1 2
5
−

=
Boundary Conditions
All internal nodes are at
for This can be
represented as,
.
3
,
2
,
1
,
0
all
for
25
100
5
0
=






=

=
j
C
T
C
T
j
j
C

20
sec
0
=
t
1,2,3,4
all
for
,
20
0
=

= i
C
Ti

5. pdepe Solves the Following
✓ pdepe solves PDEs of the form:
✓ For t = t0 and all x, the solution components satisfy initial conditions of the form
✓ For all t and either x = a or x = b, the solution components satisfy a boundary condition of the
form
𝒄 𝒙, 𝒕, 𝒖,
𝝏𝒖
𝒅𝒙
𝝏𝒖
𝒅𝒙
= 𝒙−𝒎
𝝏
𝒅𝒙
𝒙𝒎
𝒇 𝒙, 𝒕, 𝒖,
𝝏𝒖
𝒅𝒙
+ 𝒔 𝒙, 𝒕, 𝒖,
𝝏𝒖
𝒅𝒙
𝒖 𝒙, 𝒕𝒐 = 𝒖𝒐(𝒙)
𝒑 𝒙, 𝒕, 𝒖 + 𝒒 𝒙, 𝒕 𝒇 𝒙, 𝒕, 𝒖,
𝝏𝒖
𝒅𝒙
= 𝟎
m=0 for Cartesian,1 for cylindrical,
2 for spherical
Initial Conditions
Boundary Conditions –
one at each boundary
Elements of q are either identically zero or never zero. Note that the boundary conditions are expressed in terms
of the flux f rather than ∂u/∂x. Also, of the two coefficients, only p can depend on u.

6. Pdepe solver has six sub-function
In the call sol
✓ M → geometry of the system
✓ pdefun → PDE parameters
✓ Icfun → initial conditions
✓ bcfun → boundary conditions
✓ xmesh → distance
✓ tspan → time span
s𝑜𝑙 = 𝑝𝑑𝑒𝑝𝑒(𝑚, 𝑝𝑑𝑒𝑓𝑢𝑛, 𝑖𝑐𝑓𝑢𝑛, 𝑏𝑐𝑓𝑢𝑛, 𝑥𝑚𝑒𝑠ℎ, 𝑡𝑠𝑝𝑎𝑛)

7. Matlab Coding for pde
✓ m corresponds to m.
✓ xmesh(1) and xmesh(end) correspond to a and b.
✓ tspan(1) and tspan(end) correspond to t0 and tf.
✓ pdefun computes the terms c, f, and s . It has the form
❖ [c,f,s] = pdefun(x,t,u,dudx)
✓ icfun evaluates the initial conditions. It has the form
❖ u = icfun(x)
✓ bcfun evaluates the terms p and q of the boundary conditions. It has the form
❖ [pl,ql,pr,qr] = bcfun(xl,ul,xr,ur,t)

8. Our equation
𝑐 = 1/𝛼, u = T, m = 0 , s = 0, f =
𝜕𝑇
𝜕𝑥
2
2
1
x
T
t
T


=


 C
k

 =
𝒄
𝝏𝒖
𝜕𝒕
= 𝒙−𝒎
𝝏
𝜕𝒙
𝒙𝒎
𝒇 + 𝒔

9. Boundary Conditions
𝒑 𝒙, 𝒕, 𝒖 + 𝒒 𝒙, 𝒕 𝒇 𝒙, 𝒕, 𝒖,
𝝏𝒖
𝒅𝒙
= 𝟎
Elements of q are either identically zero or never zero. Note that the boundary conditions are expressed in terms
of the flux f rather than ∂u/∂x. Also, of the two coefficients, only p can depend on u.
0
=
i 1 2 3 4 5
m
01
.
0
C
T 
= 25
C
T 
=100
At x=0 (Left side)
pl=ul-100;
ql=0;
At x=0.05 (Right side)
pr=ur-25;
ql=0;
𝒑 + 𝒒
𝝏𝒖
𝒅𝒙
= 𝟎 This equation applied both
left and right side

10. Matlab Code
%solving paraboloc heat conduction equation using matlab pde solver
function pde_prabolic
global alpha
%the given constant value
k=54;
rho=7800;
cp=490;
alpha=k/(rho*cp);
%the problem is cartesioan so m=0
m=0;

11. Code Cont…
%the length of the road is 0.05m and divede with 0.01m length
x=linspace(0,0.05,6);
%the given time span 0 to 9 secon with 3 second step size
t=linspace(0,9,4);
%the pde solution
sol=pdepe(m,@pdex1pde,@pdex1ic,@pdex1bc,x,t);
%remeber our u is Temperature
u=sol(:,:,1)
%graph of our solution
surf(x,t,u)

12. Code Cont…
xlabel('Length of the road')
ylabel('time in (second)')
figure
plot(x,u,'--o','linewidth',1)
xlabel('Length of the road')
ylabel('time in (second)')
legend('intial at 0 sec','at 3 sec','at 6 sec',' at 9 sec')

13. Code Cont…
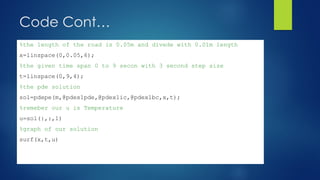
%now we will code all the program required to get the solution of pde
%our pde function
function [c,f,s]=pdex1pde(x,t,u,DuDx)
global alpha
c=1/alpha;
f=DuDx;
s=0;
%intial condion
function u0=pdex1ic(x,t,u,DuDx)
u0=20;
%boundary function
function [pl,ql,pr,qr]=pdex1bc(xl,ul,xr,ur,t)
pl=ul-100;
ql=0;
pr=ur-25;
qr=0;
% now we are ready to get the solution
%we can also get numerical soultion instead of plot

14.  Click the link below to see the procedure on youtube
 Solving heat conduction equation using matlab pde solver -
YouTube