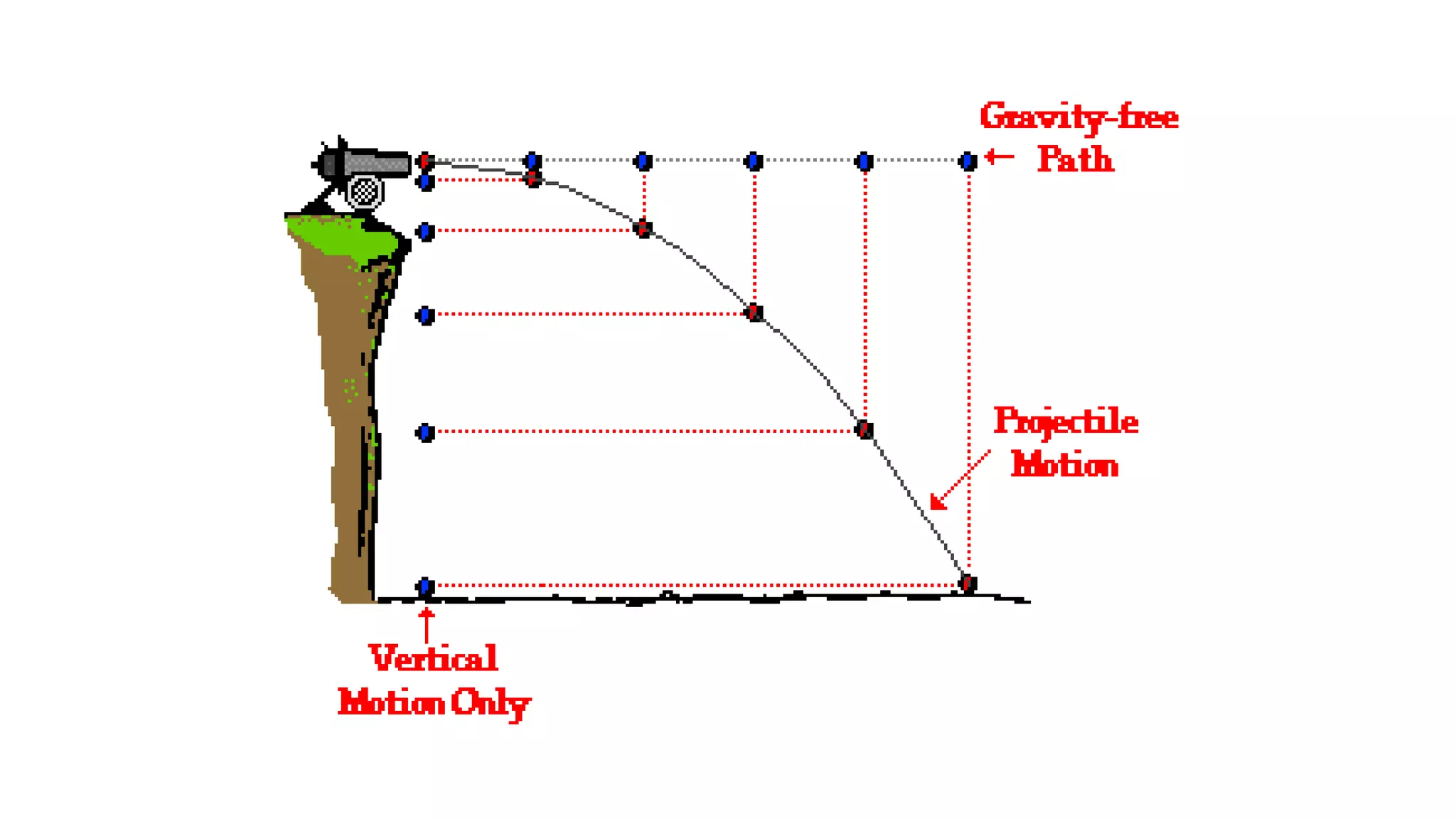
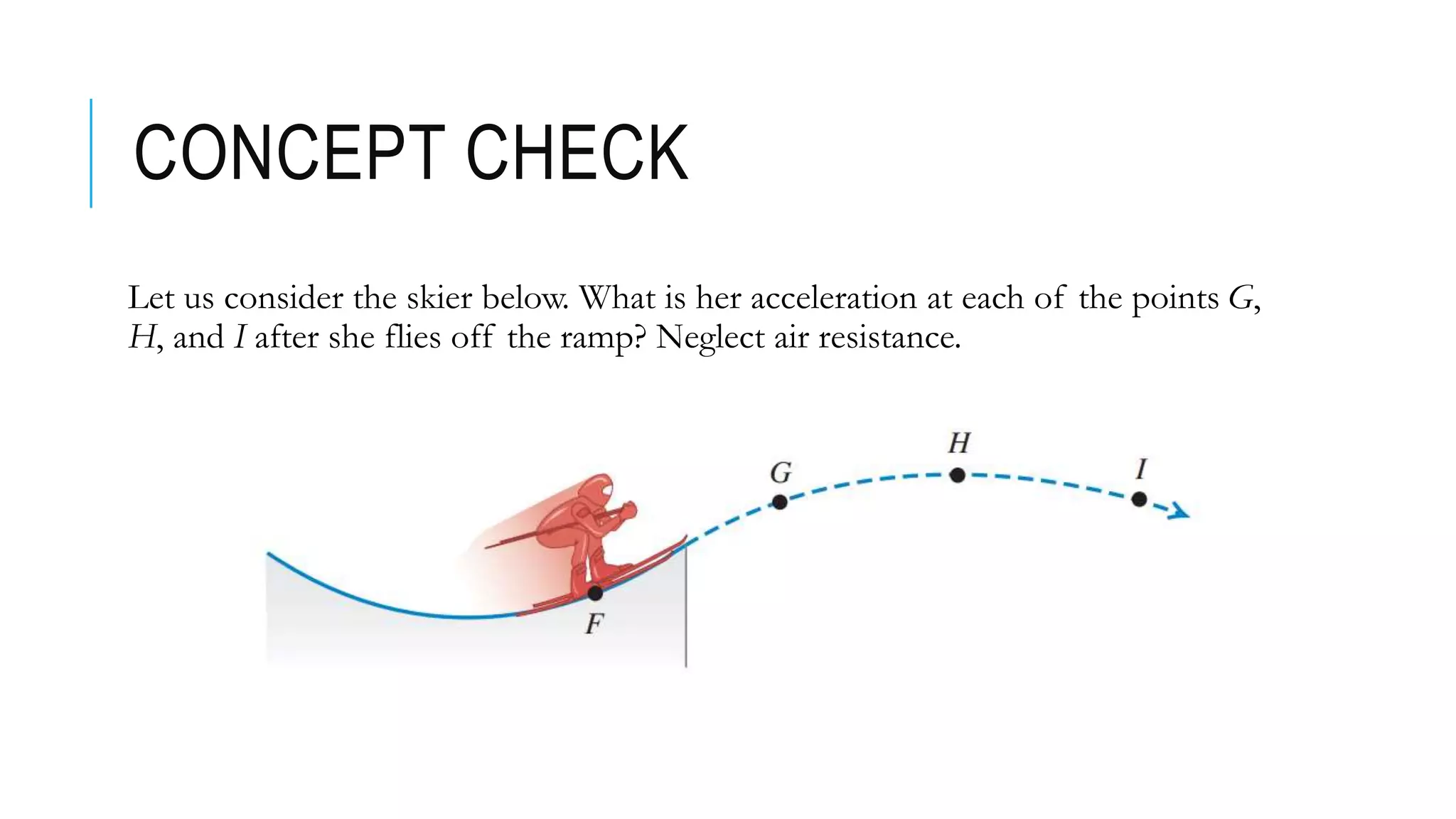
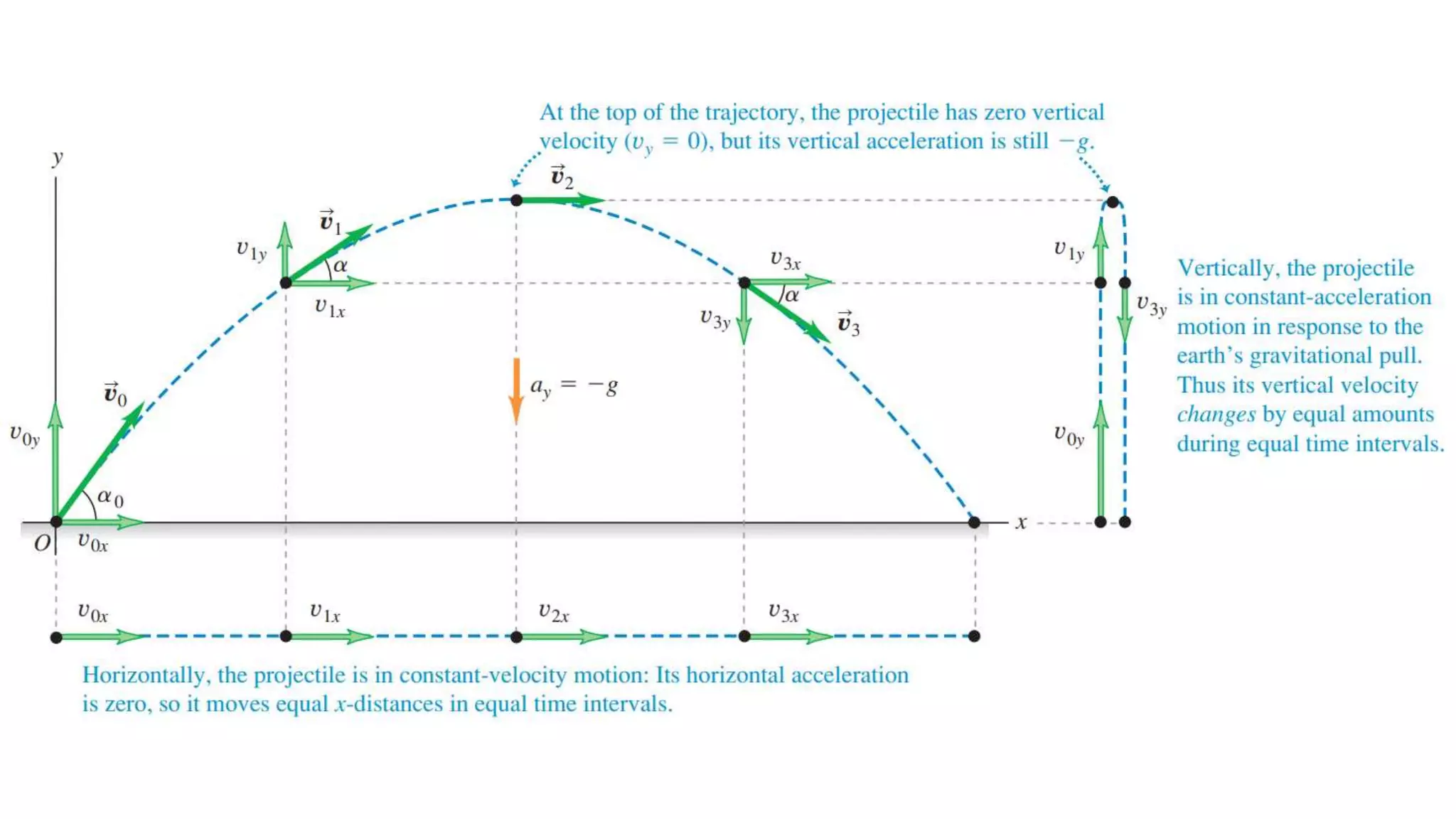
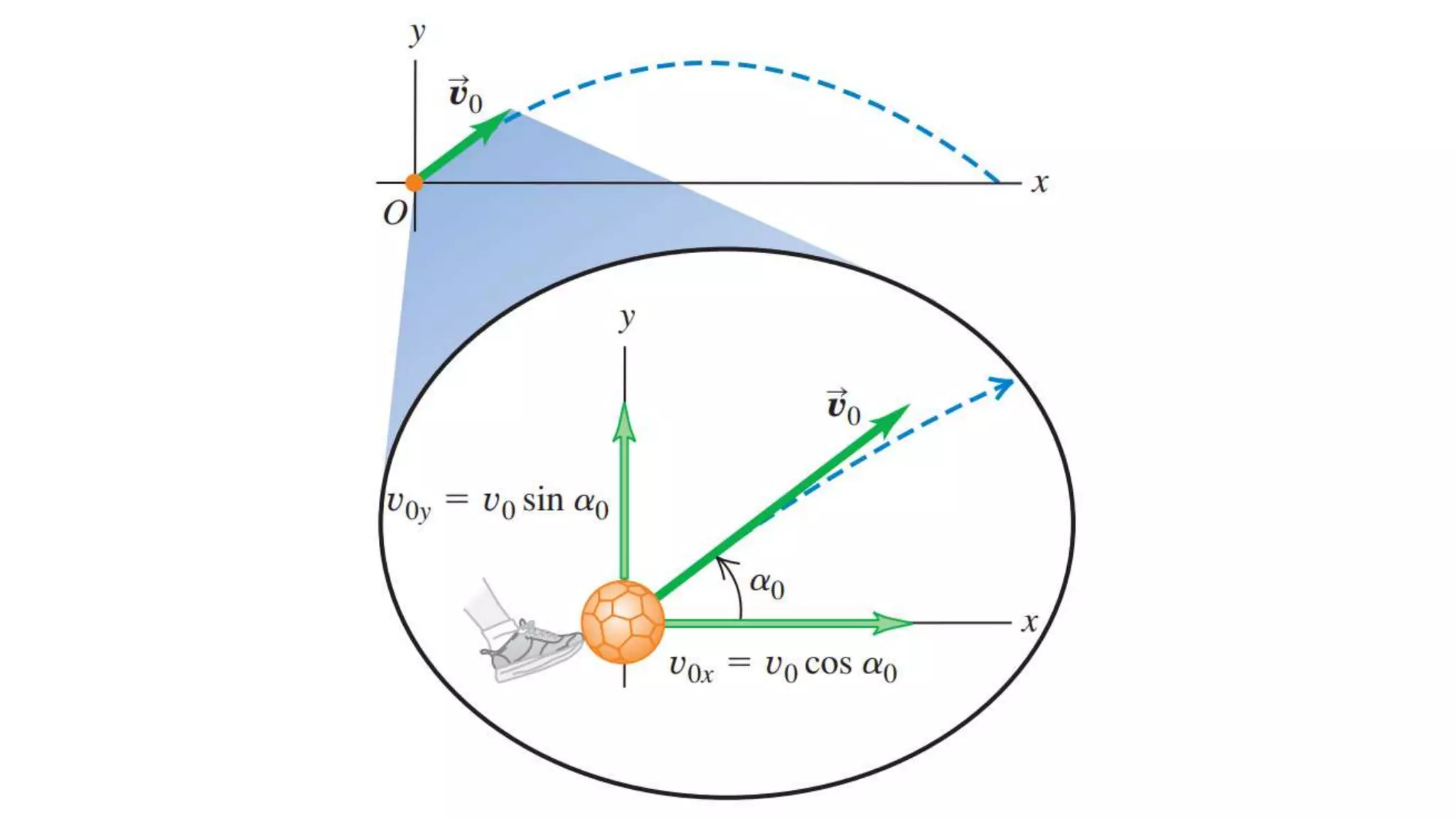
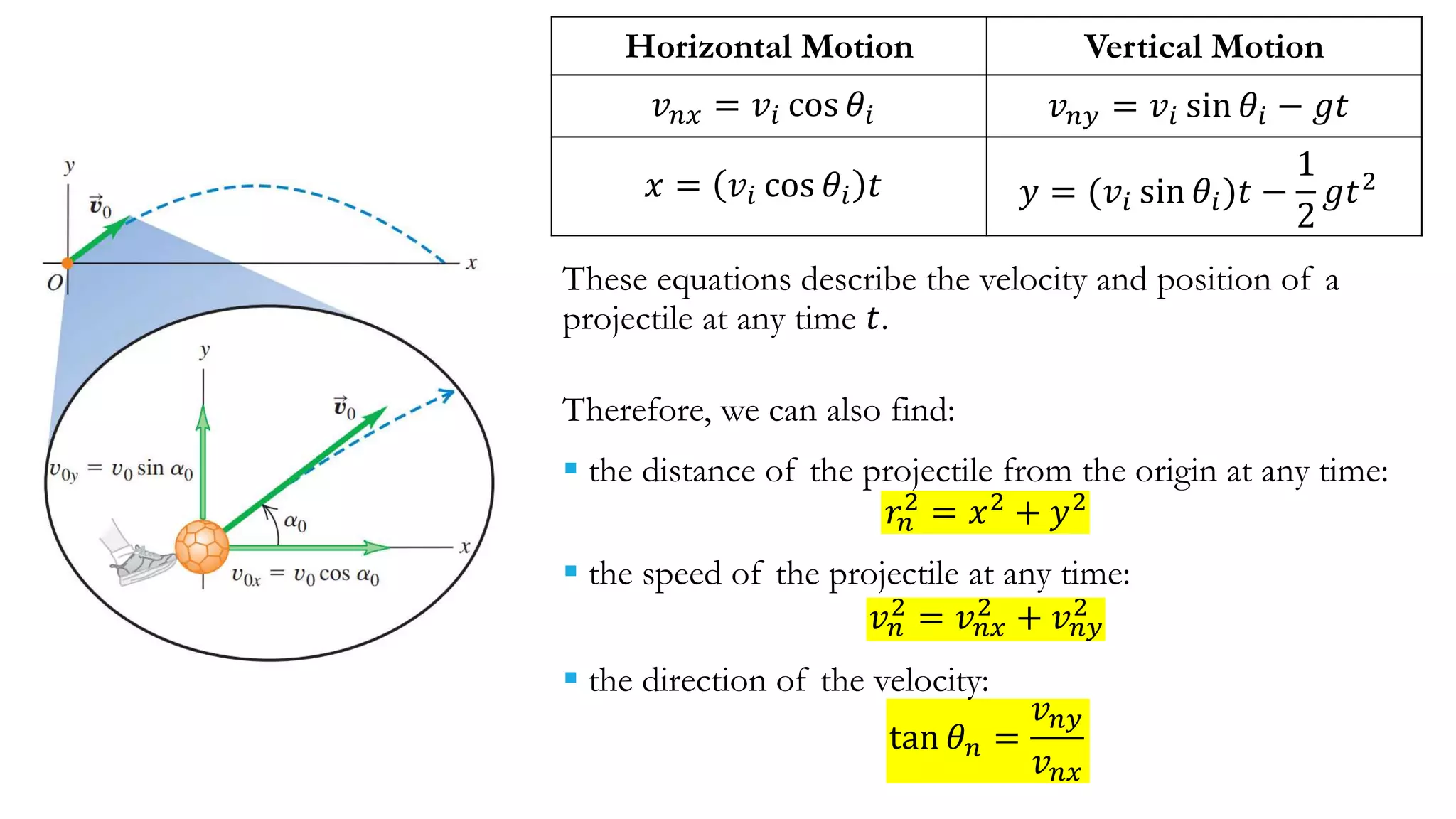
This document discusses projectile motion and Galileo's experiments showing that all objects fall at the same rate regardless of mass when air resistance is negligible. It provides equations to describe the horizontal and vertical motion of a projectile. These equations can be used to find the distance, speed, direction, and trajectory of a projectile at any given time. The document also discusses how projectile motion is a combination of horizontal and vertical motion and provides examples of calculating values like time, distance, position, and velocity for various projectile scenarios.

1. PROJECTILE
MOTION
Prepared by:
JUNIEL D. BARRIOS, LPT
Secondary School Teacher I

2. ARISTOTLE’S THEORY OF GRAVITY
Objects fall at speed that is directly proportional to their mass.

3. LEANING TOWER OF PISA
EXPERIMENT
But Galileo has proven that in actuality, objects fall at the
same speed regardless of their mass given that air resistance
is negligible.

4. LEANING TOWER OF PISA EXPERIMENT
ON THE MOON
The recreation of Galileo’s experiment by the Apollo 15
astronaut, David Scott, using hammer and feather has
further supported the notion that objects fall at the same
speed regardless of their mass.

5. CONCEPT CHECK
If two objects are released at the same time, but one object is simply dropped,
while the other object is thrown horizontally, will they also land at the same time?

7. X- AND Y-DIMENSION
INDEPENDENCE
Projectile motion is therefore a combination of horizontal motion with constant velocity and
vertical motion with constant acceleration.
Horizontal Motion Vertical Motion
𝑎𝑥 = 0 𝑎𝑦 = −𝑔
𝑣𝑛𝑥 = 𝑣𝑖𝑥 𝑣𝑛𝑦 = 𝑣𝑖𝑦 − 𝑔𝑡
𝑥 = 𝑣𝑖𝑥𝑡 𝑦 = 𝑣𝑖𝑦𝑡 −
1
2
𝑔𝑡2

8. CONCEPT CHECK
Let us consider the skier below. What is her acceleration at each of the points G,
H, and I after she flies off the ramp? Neglect air resistance.

10. CONCEPT CHECK
A male eagle in level flight 150 meters above the ground drops the fish it caught
as it fell in love at first sight with the female eagle going to the opposite direction.
If the male eagle’s horizontal speed is 28 meters per second, how far ahead of
the drop point will the fish land?

11. CONCEPT CHECK
A ghost moved the toy car off the edge of a table that is 2 meters high and lands
0.5 meter from the base of the table. (a) How much time had passed between the
moment the toy car left the table and the moment it hit the floor? (b) What was
the horizontal velocity of the toy car when it hit the floor?

12. PROJECTILE
MOTION
Prepared by:
JUNIEL D. BARRIOS, LPT
Secondary School Teacher I

13. RECALL!
A ping pong ball leaves a 0.8-meter high table with an initial horizontal velocity
of 3 meters per second. Calculate the time required for the ping pong ball to fall
to the ground and the horizontal distance between the table’s edge and the ping
pong ball’s landing location.

15. Horizontal Motion Vertical Motion
𝑣𝑛𝑥 = 𝑣𝑖 cos 𝜃𝑖 𝑣𝑛𝑦 = 𝑣𝑖 sin 𝜃𝑖 − 𝑔𝑡
𝑥 = 𝑣𝑖 cos 𝜃𝑖 𝑡 𝑦 = (𝑣𝑖 sin 𝜃𝑖)𝑡 −
1
2
𝑔𝑡2
These equations describe the velocity and position of a
projectile at any time 𝑡.
Therefore, we can also find:
 the distance of the projectile from the origin at any time:
𝑟𝑛
2 = 𝑥2 + 𝑦2
 the speed of the projectile at any time:
𝑣𝑛
2 = 𝑣𝑛𝑥
2 + 𝑣𝑛𝑦
2
 the direction of the velocity:
tan 𝜃𝑛 =
𝑣𝑛𝑦
𝑣𝑛𝑥

16. PARABOLIC TRAJECTORY
Equation of a Parabola:
𝑦 = 𝑏𝑥 − 𝑐𝑥2
Shape of the Trajectory:
𝑦 = (tan 𝜃𝑖) 𝑥 −
𝑔
2𝑣𝑖
2
cos2 𝜃𝑖
𝑥2

17. CONCEPT CHECK
What angle provides the greatest height in projectile motion?
90 degrees
Prove it mathematically.
𝑦 =
𝑣𝑖
2
sin2
𝜃𝑖
2𝑔

18. CONCEPT CHECK
What angle provides the greatest range in projectile motion?
45 degrees
Prove it mathematically.
𝑥 =
𝑣𝑖
2
sin 2𝜃𝑖
𝑔

19. CONCEPT CHECK
A motorcycle stunt rider rides off the edge of a cliff. Just at the edge, his
horizontal velocity equates to 9.3 m/s. What is his position—distance from the
edge of the cliff—and velocity 0.7 s after he leaves the edge of the cliff?

20. CONCEPT CHECK
A batter hits a baseball so that it leaves the bat at speed 𝑣𝑖 = 37.5 m/s at an
angle 𝜃𝑖 = 51.3°. (a) Find the position of the ball and its velocity at 𝑡 = 2.2 s.
(b) Find the time when the ball reaches the highest point of its flight, and its
height at this time. (c) Find its range.

21. Thank You!