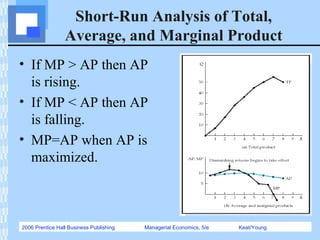
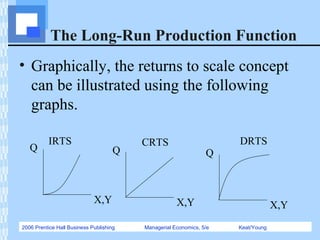
This document provides an overview of production functions and their estimation. It defines short-run and long-run production functions, the law of diminishing returns, and the three stages of production. It also discusses forms of production functions like Cobb-Douglas, and how to statistically estimate parameters of these functions using techniques like linear regression. Production functions are important tools for managerial decision-making around capacity planning and input usage.