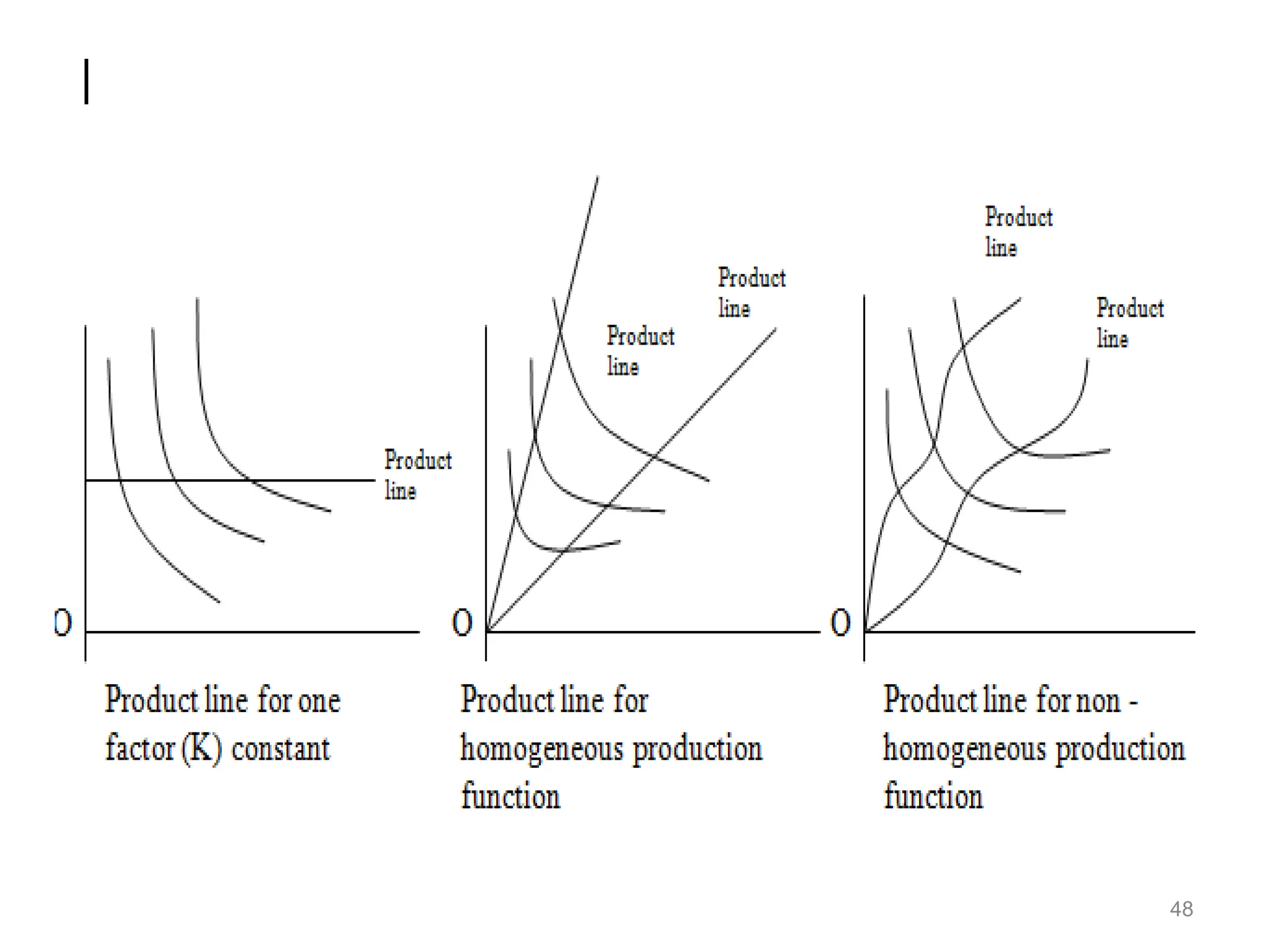
eeeeeeeebfffffffffffffffffffffffffffffffffffffffffffffffffffffffffffhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhhkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk



















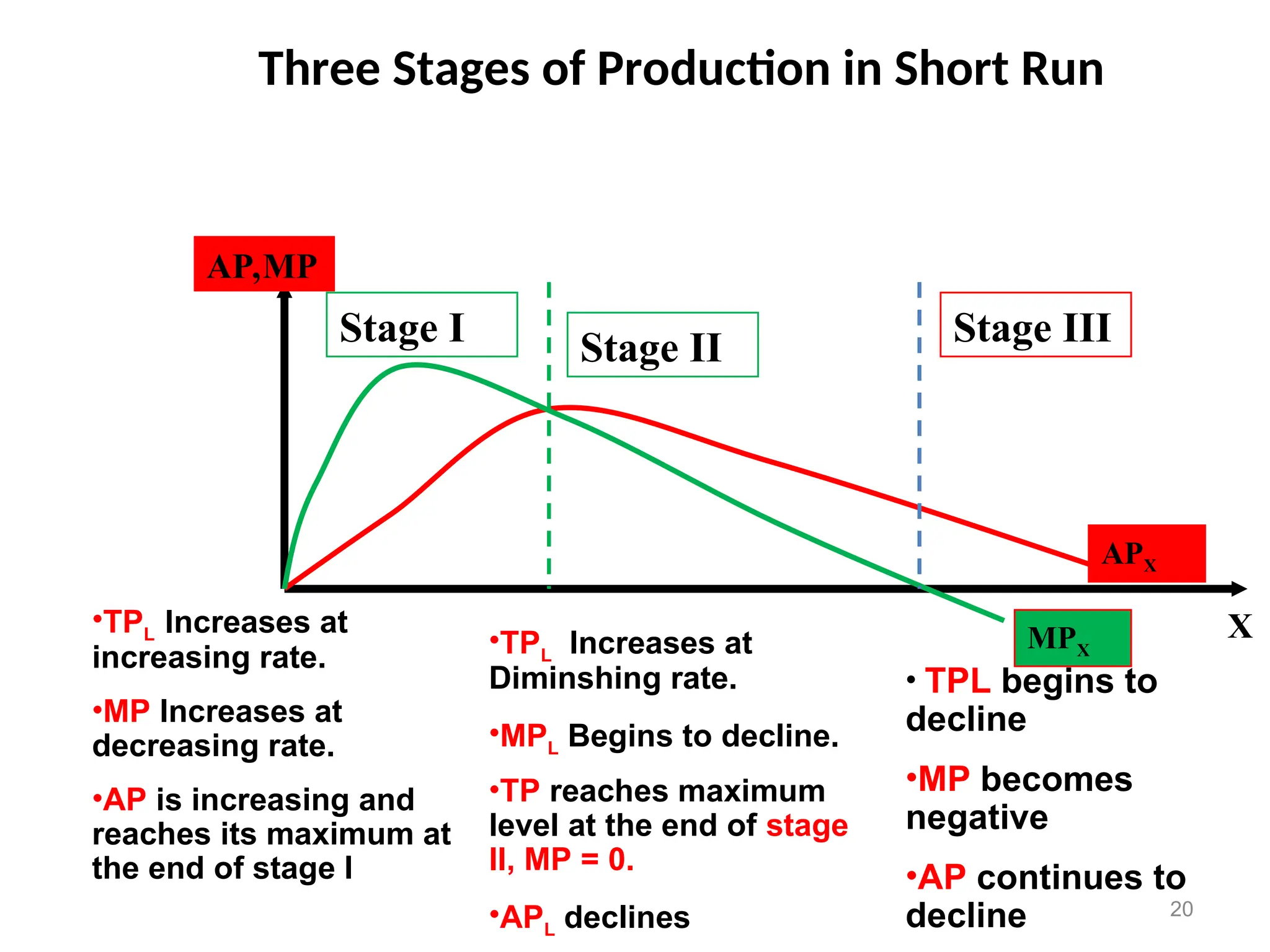








![How much will output increase when ALL inputs
increase by a particular amount?
RTS = [%Q] / [%(all inputs)]
1% increase in inputs => more than 1% increase in
output, increasing returns to scale.
1% increase in inputs => 1% increase in output
constant returns to scale.
1% increase in inputs => a less than 1% increase in
output, decreasing returns to scale.
31
Laws of Returns to Scale](https://image.slidesharecdn.com/ch3productiontheory-250413090312-029ba7ca/75/CHapter-production-theory-of-mco-eco-ppt-31-2048.jpg)