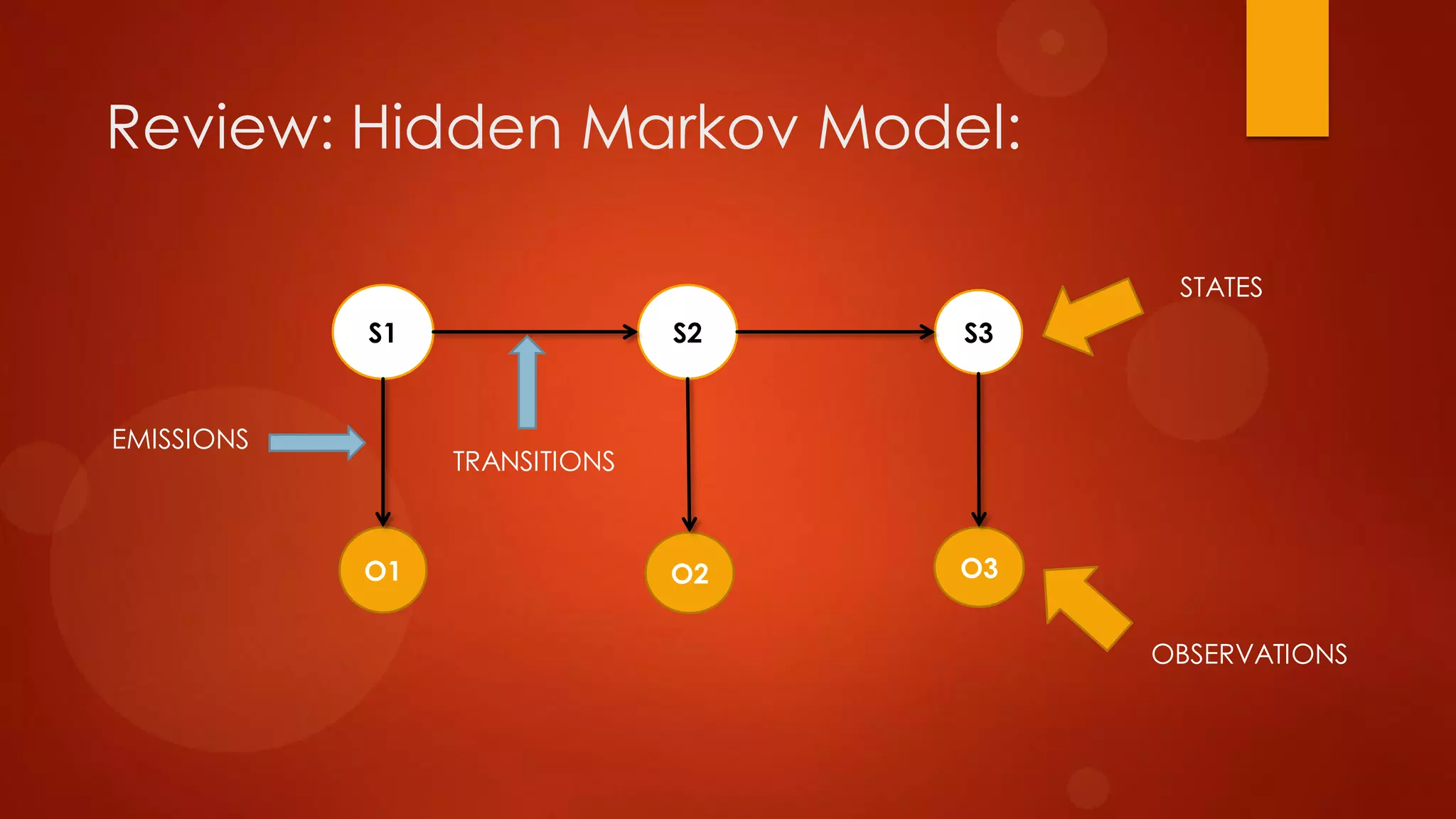
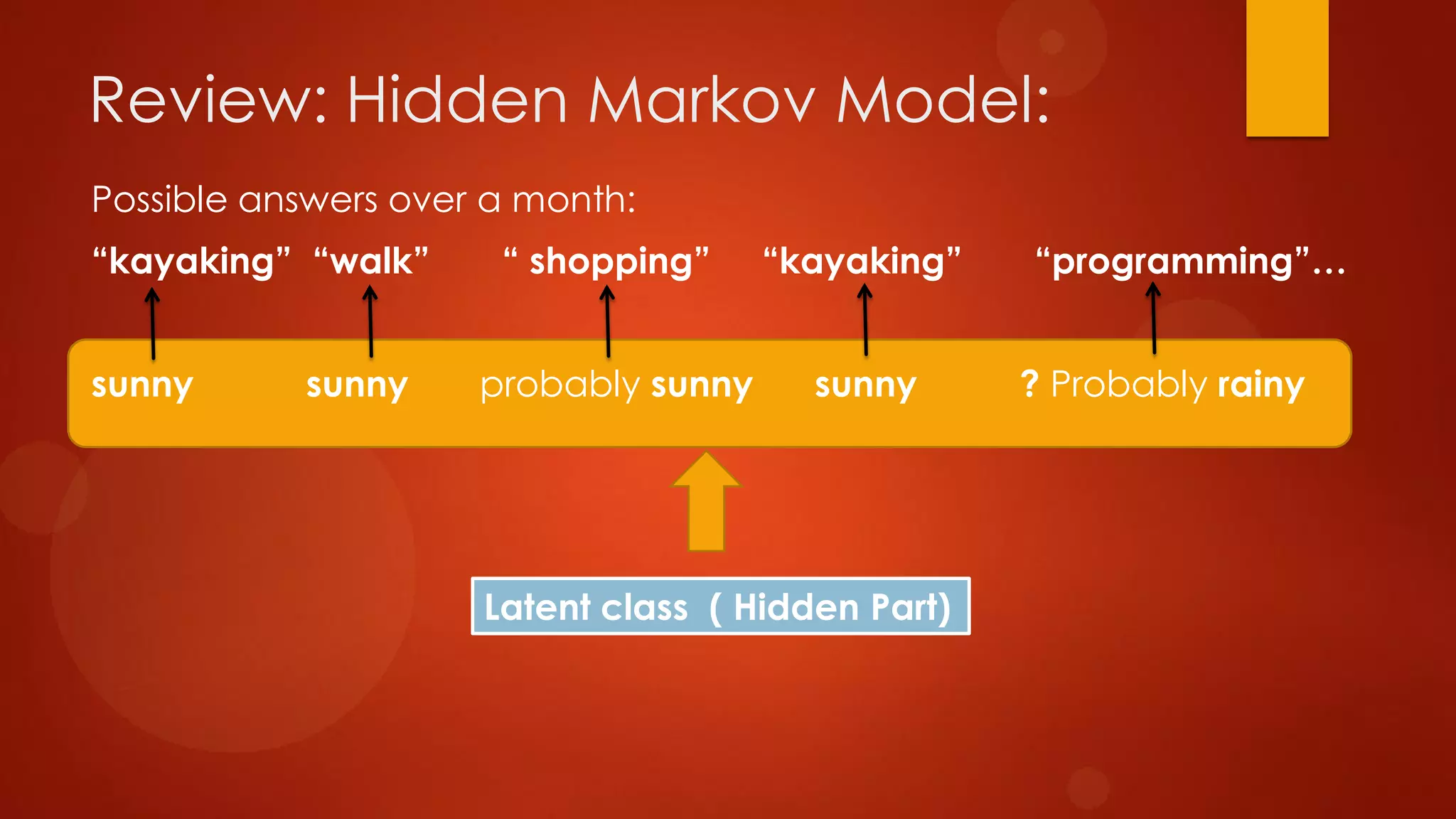
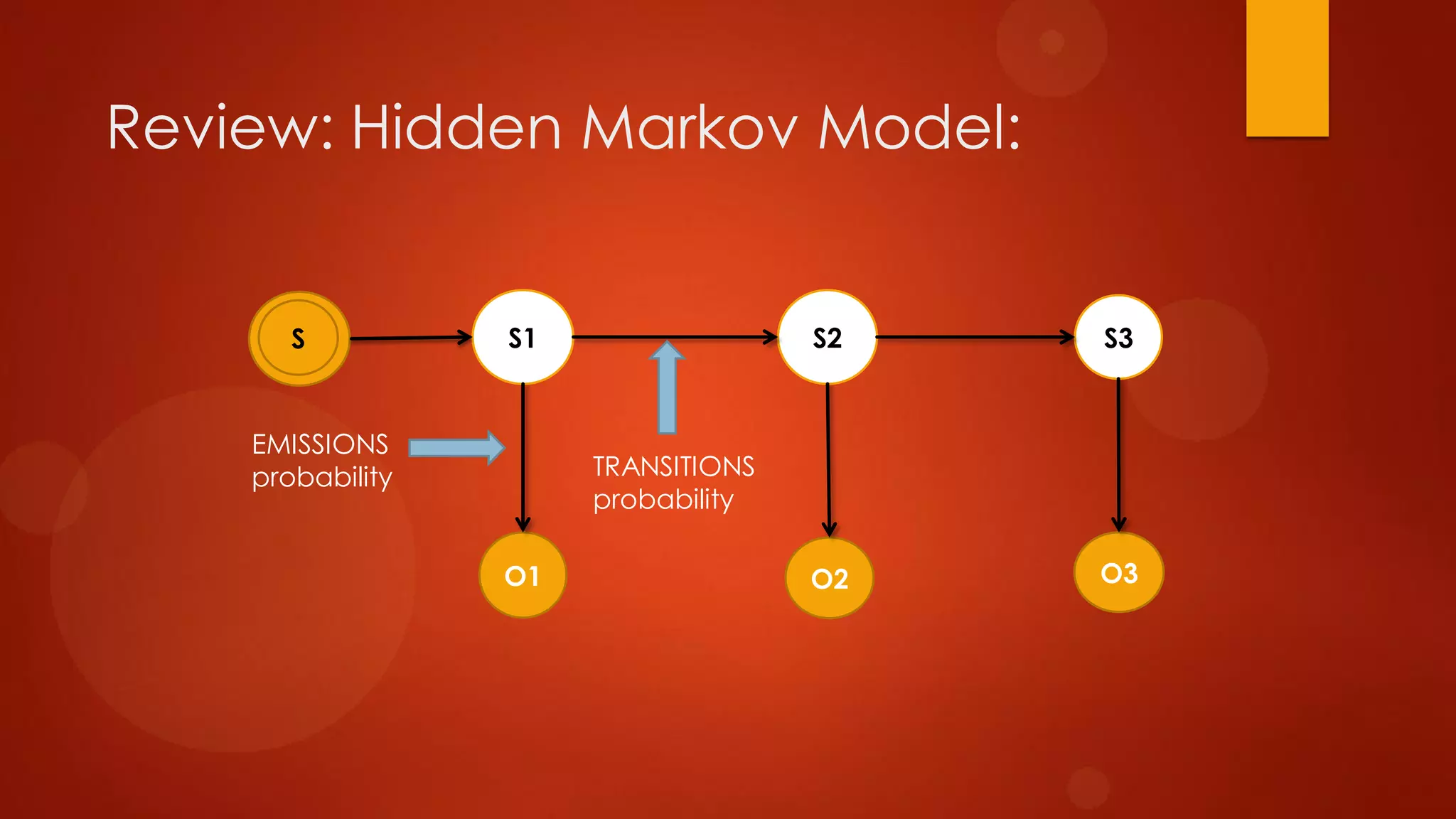
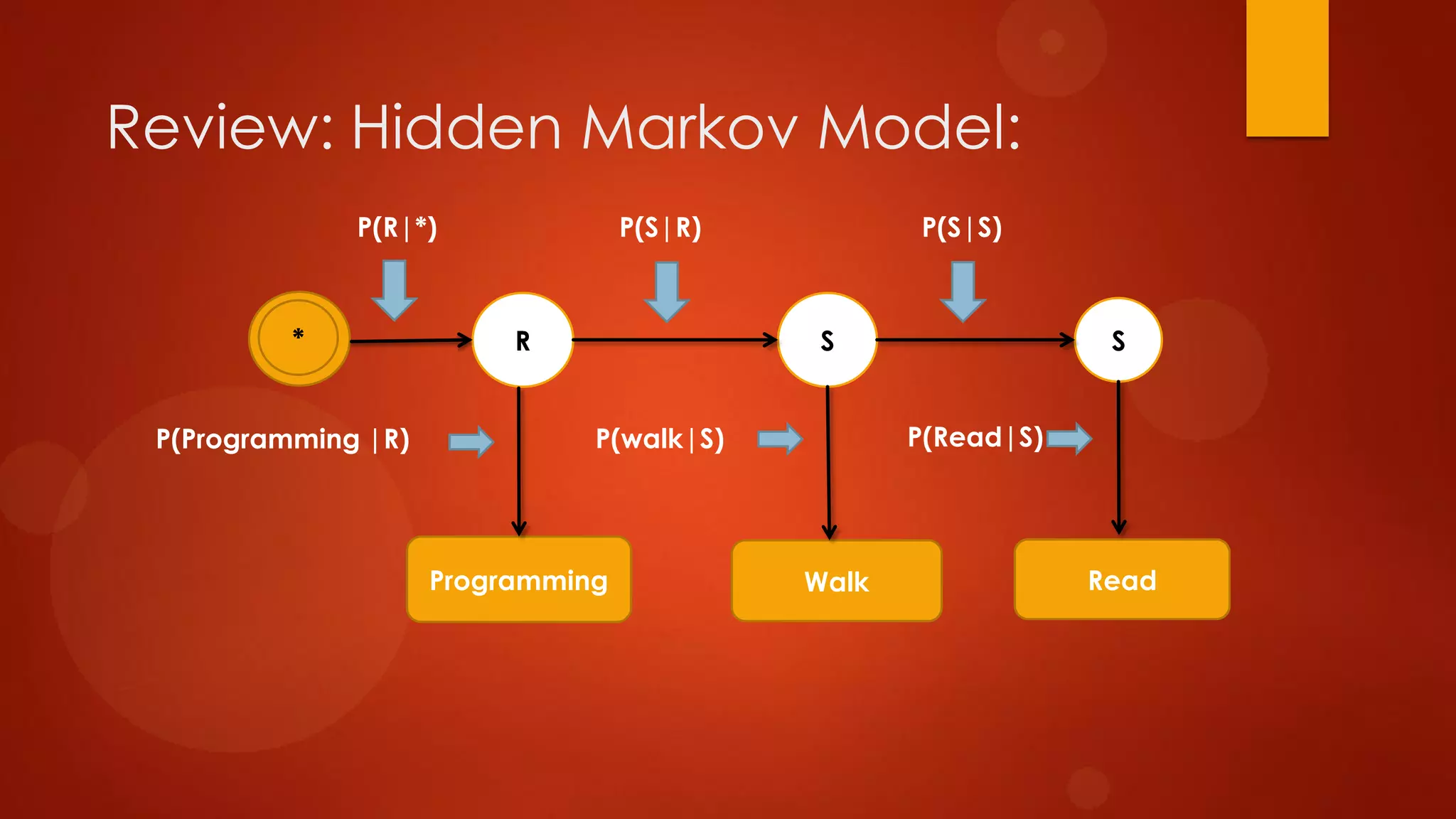
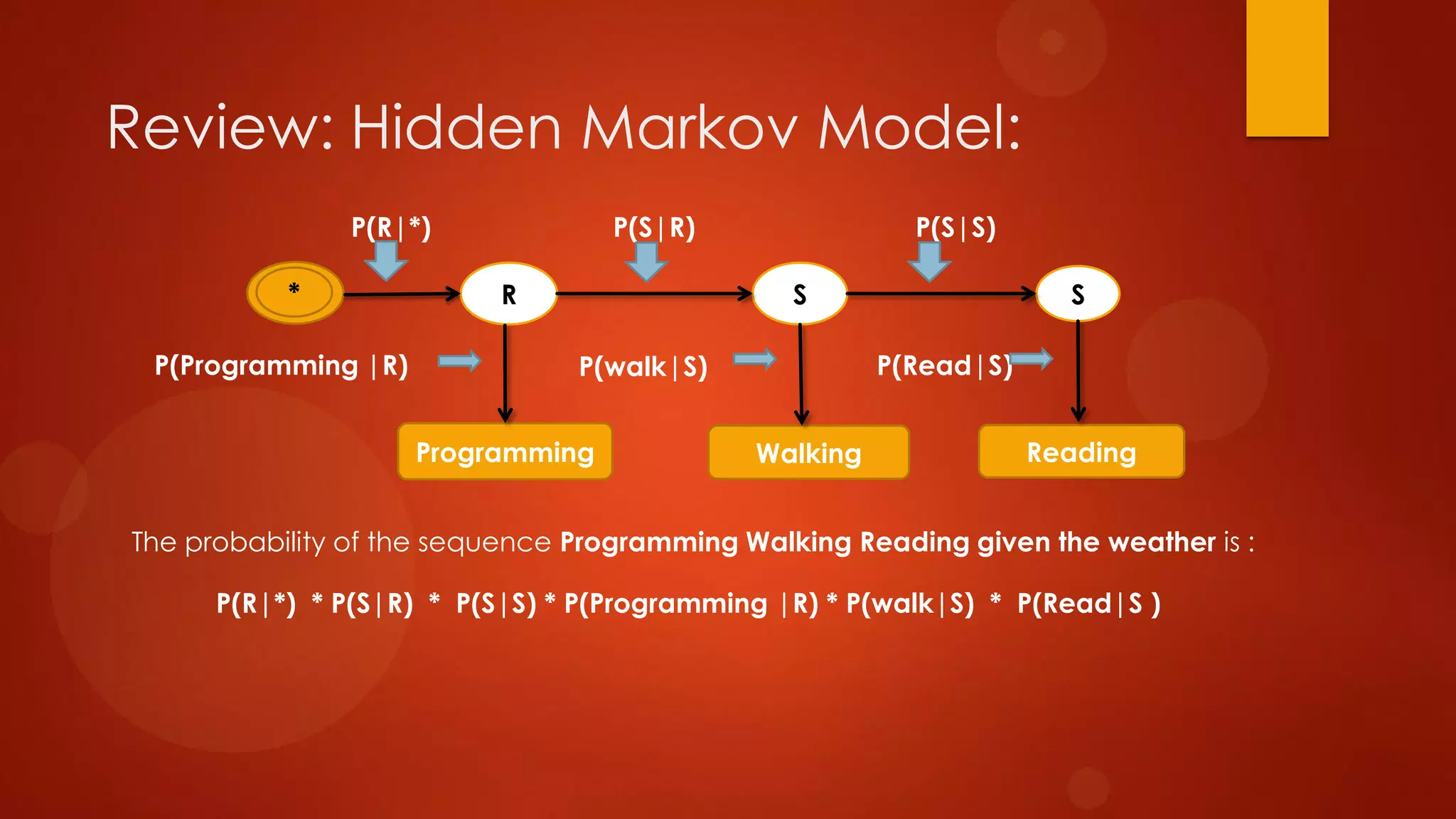
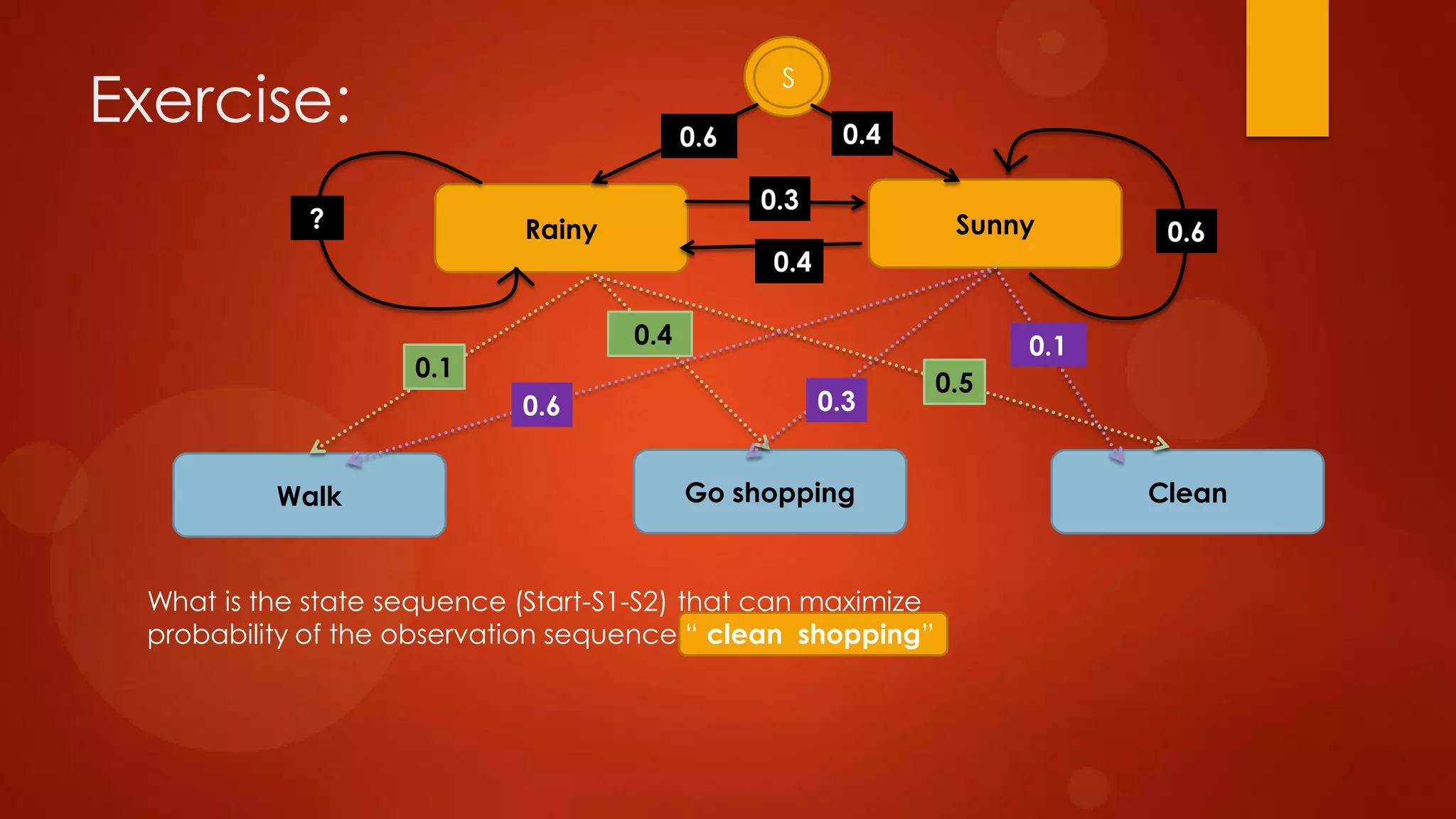
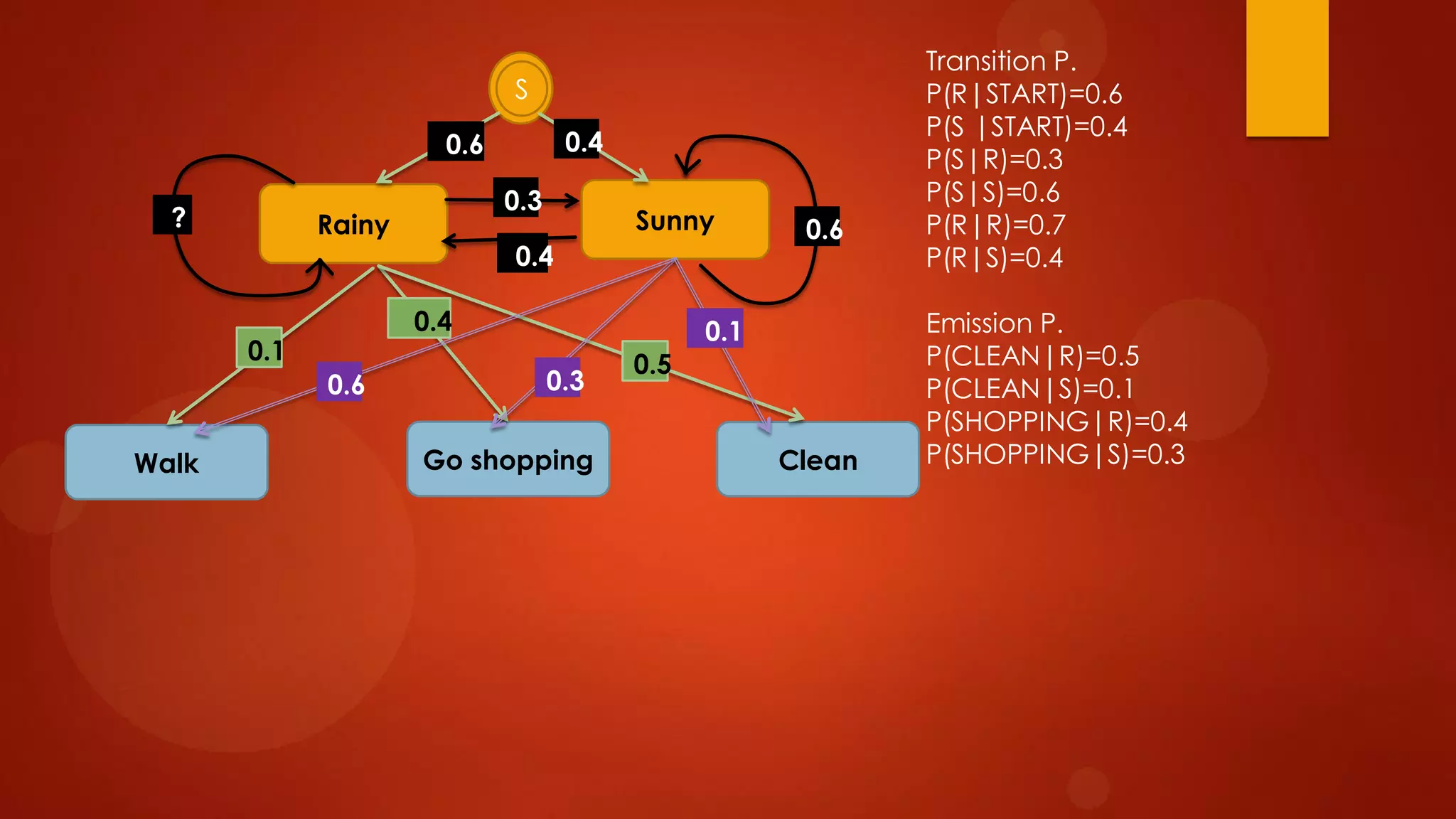
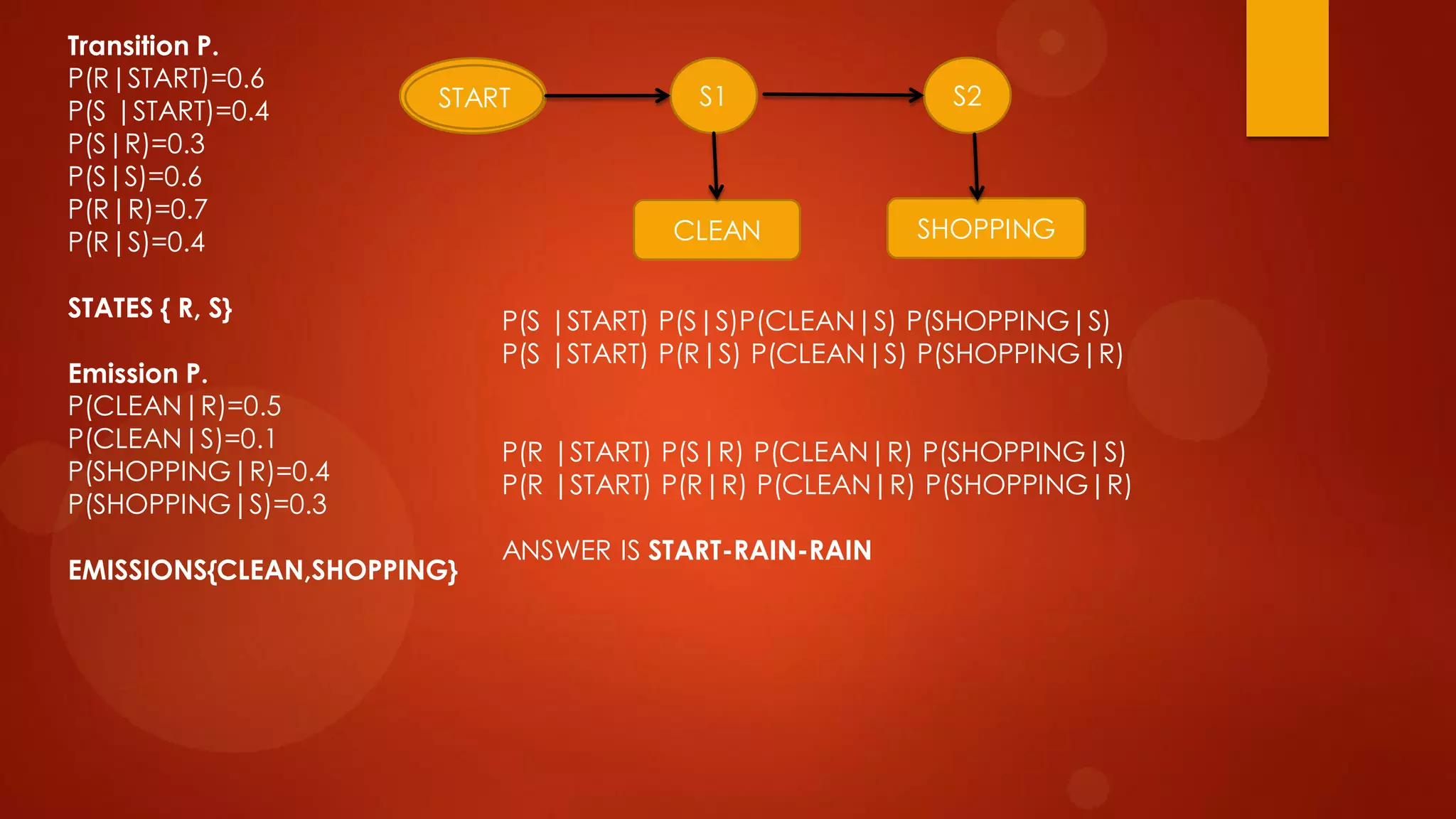
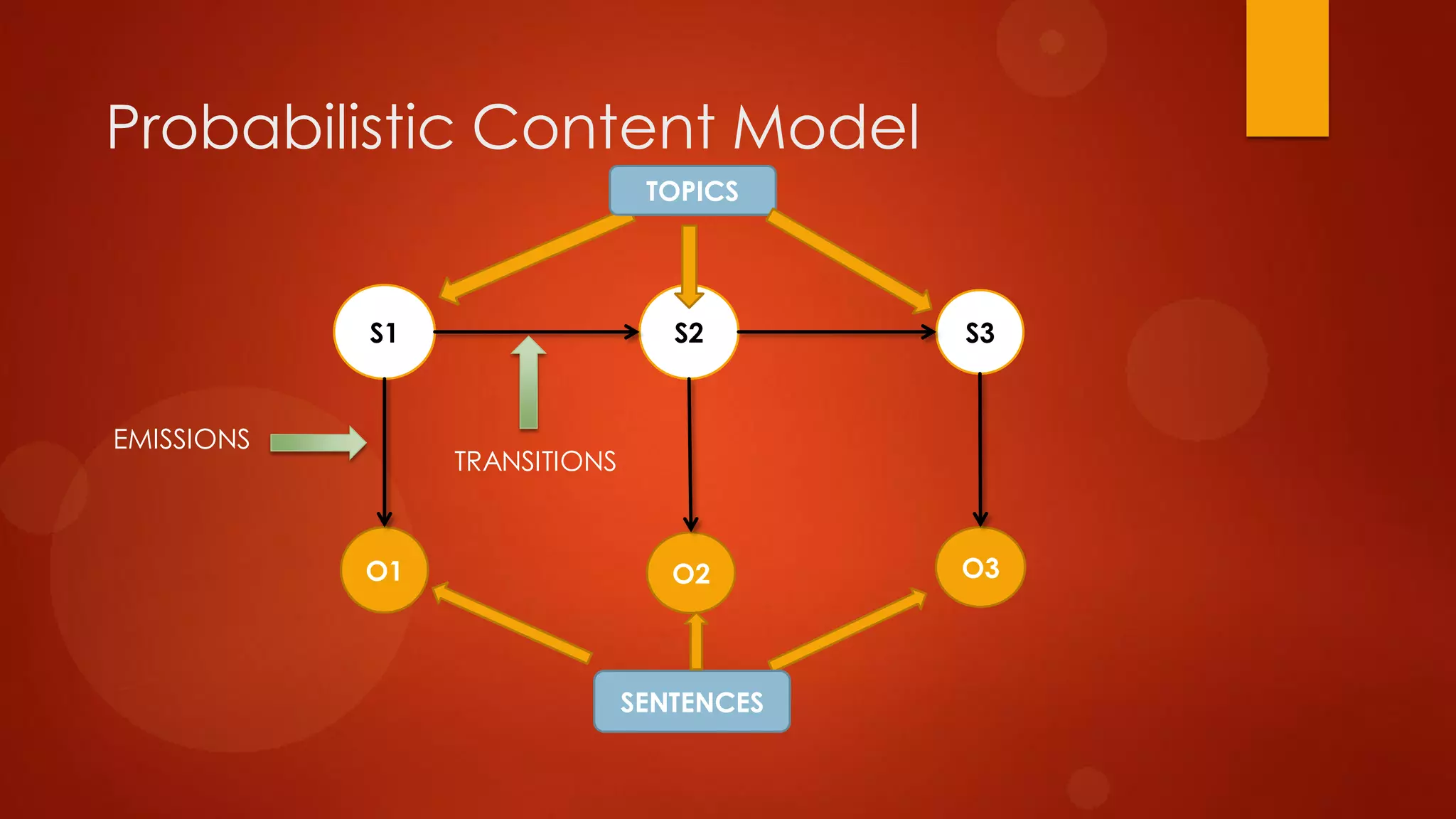
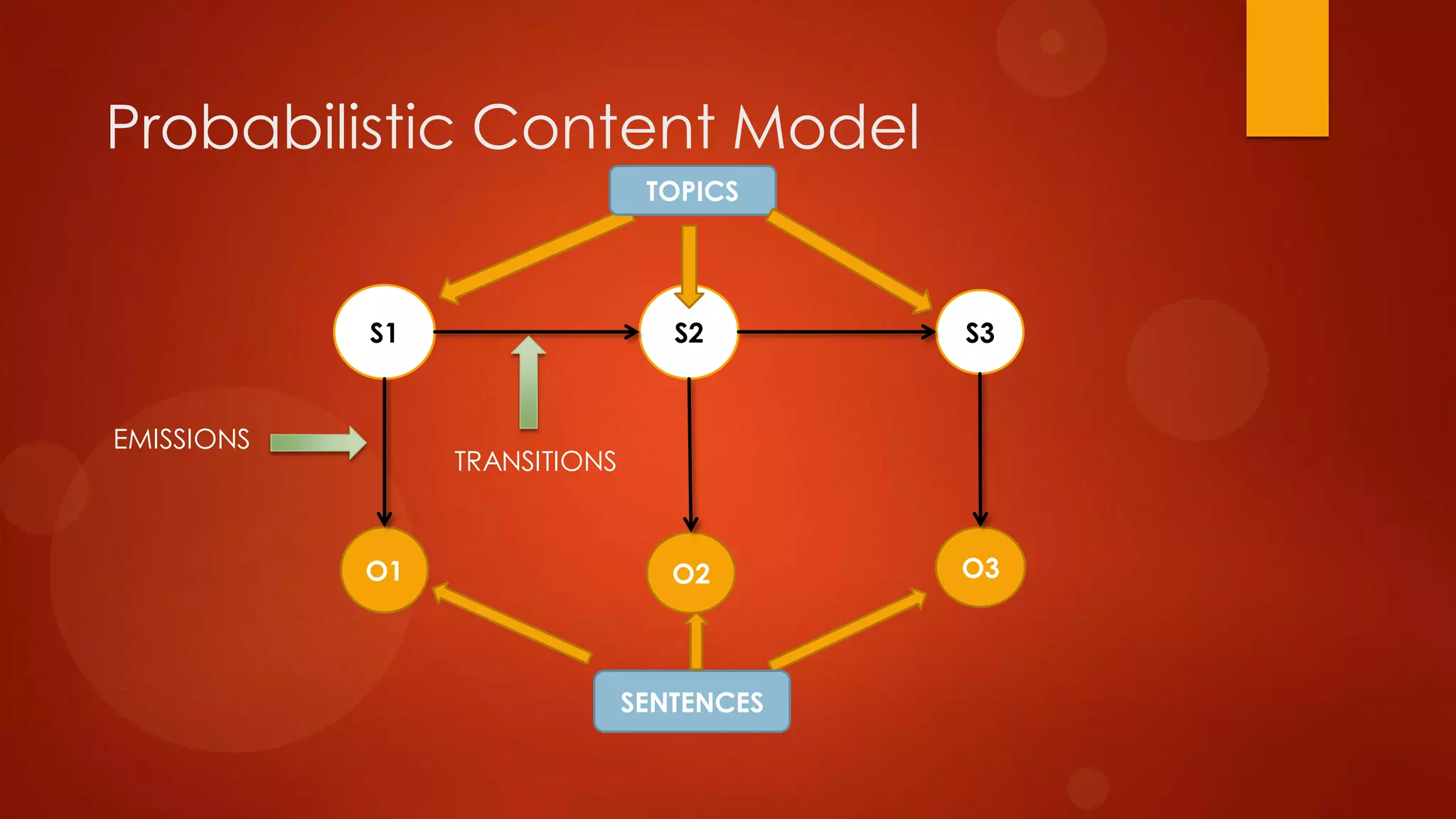
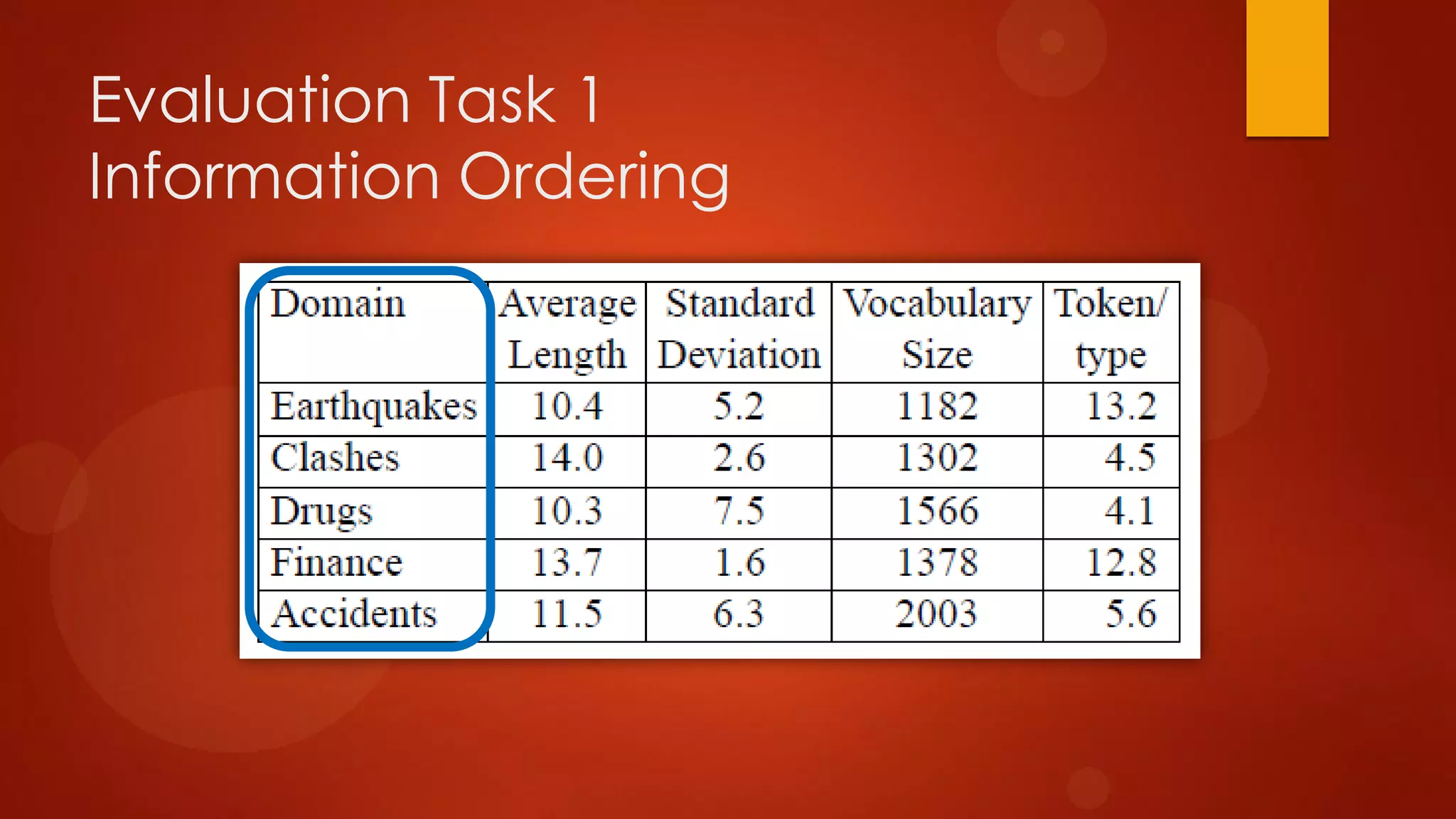
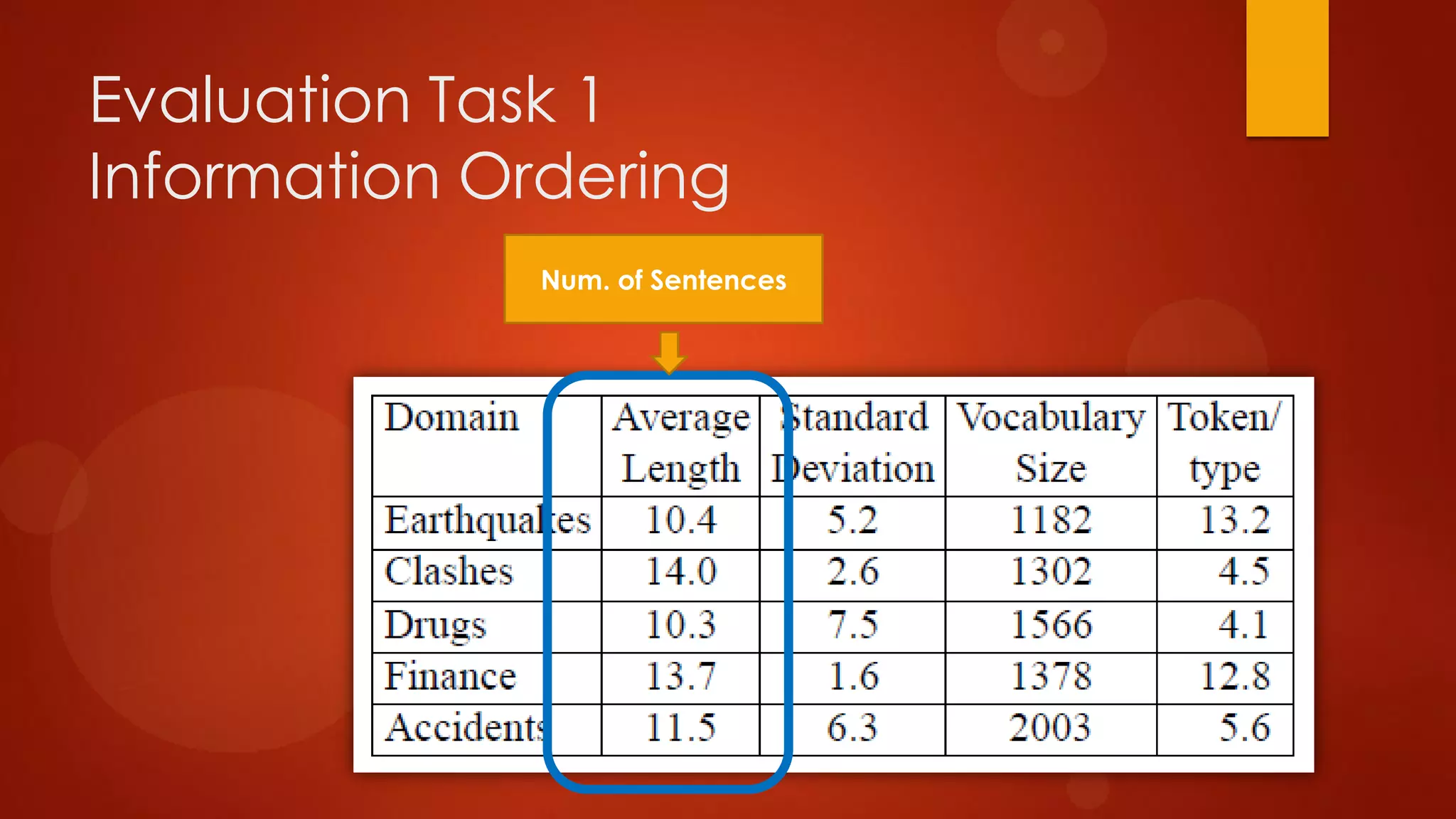
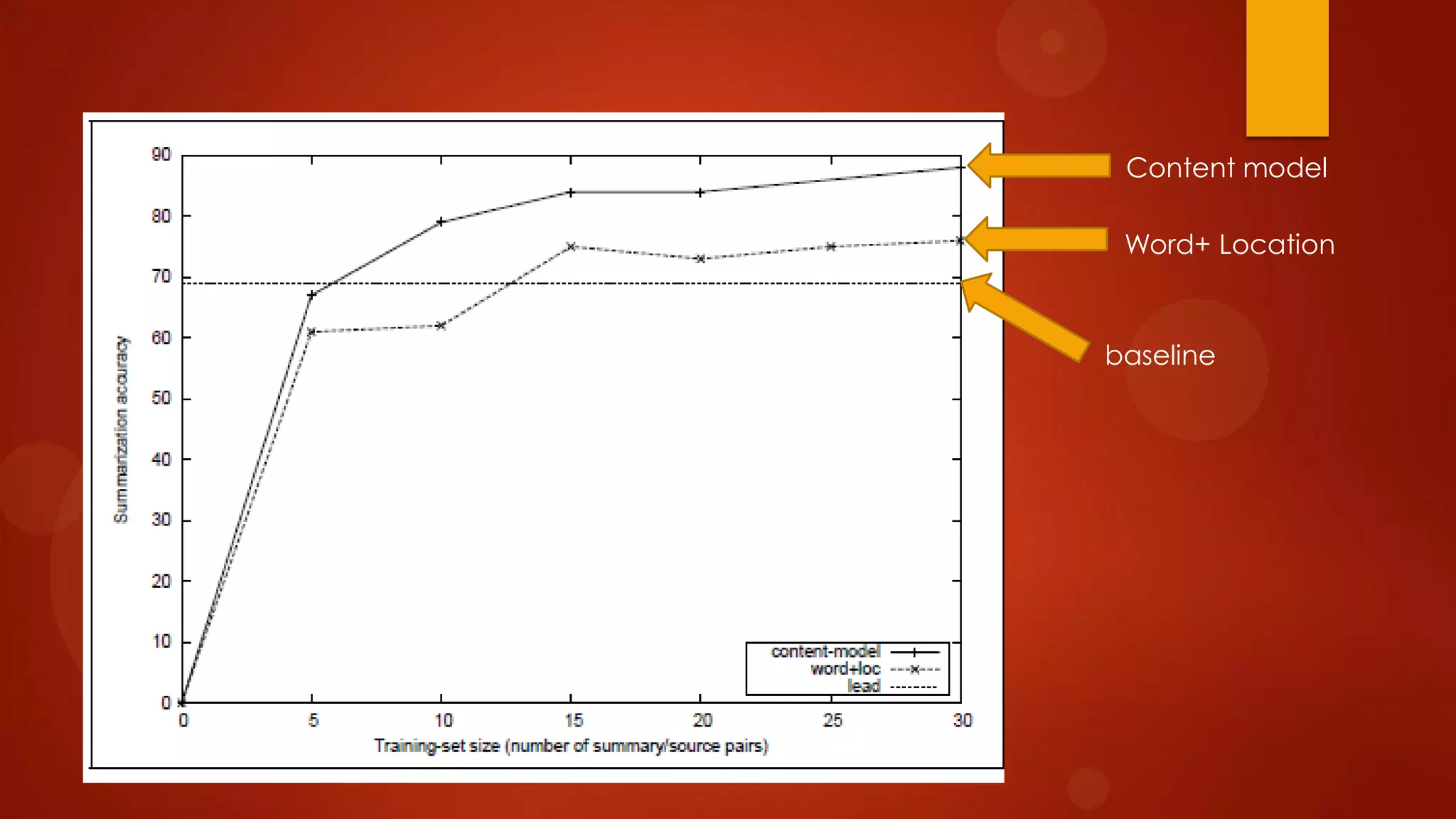
This document presents a probabilistic content model using a hidden Markov model to model topic structures in text. It applies this model to two tasks: sentence ordering and extractive summarization. For sentence ordering, it generates all possible orders, computes the probability of each, and ranks them to evaluate how well the original sentence order is recovered. For summarization, it assigns topic probabilities to sentences based on topic distributions and extracts sentences with high topic probabilities in summaries. Evaluation shows the content model outperforms baselines on both tasks, demonstrating it effectively captures text structure.

1. Probabilistic Content Model,
with Applications to Generation and Summarization
BRYAN ZHANG HANG|

2. Outline:
Goal: Modeling Topic Structures of Text
We will use:
 Hidden Markov Model
 Bigrams
 Clustering
Application:
 Sentence Ordering
 Extractive Summerization

3. Review: Hidden Markov Model:
S1 S2 S3
O1 O3O2
STATES
OBSERVATIONS
TRANSITIONS
EMISSIONS

4. Imagine :
 You call your friend who lives in a foreign country from time to tim
e. Every time you ask him or her “ What are you up to?”
 The possible answers are:
“ walk” “ice cream” “shopping”
“reading” “programming” “kayaking”
Review: Hidden Markov Model:

5. Possible answers over a month:
“kayaking” “walk” “ shopping” “kayaking” “programming”…
sunny sunny probably sunny sunny ? Probably rainy
Review: Hidden Markov Model:
Latent class ( Hidden Part)

6. Review: Hidden Markov Model:
S1 S2 S3
O1 O3O2
TRANSITIONS
probability
EMISSIONS
probability
S

7. Review: Hidden Markov Model:
R S S
Programming ReadWalk
P(Programming |R)
*
P(R|*) P(S|R) P(S|S)
P(walk|S) P(Read|S)

8. Review: Hidden Markov Model:
R S S
Programming ReadingWalking
P(Programming |R)
*
P(R|*) P(S|R) P(S|S)
P(walk|S) P(Read|S)
The probability of the sequence Programming Walking Reading given the weather is :
P(R|*) * P(S|R) * P(S|S) * P(Programming |R) * P(walk|S) * P(Read|S )

9. Exercise:
Rainy Sunny
Walk CleanGo shopping
S
0.1
0.4
0.5
0.6 0.3
0.1
0.3
0.4
0.6?
0.40.6
What is the state sequence (Start-S1-S2) that can maximize
probability of the observation sequence “ clean shopping”

10. Rainy Sunny
Walk CleanGo shopping
S
0.1
0.4
0.5
0.6 0.3
0.1
0.3
0.4
0.6?
0.40.6
Transition P.
P(R|START)=0.6
P(S |START)=0.4
P(S|R)=0.3
P(S|S)=0.6
P(R|R)=0.7
P(R|S)=0.4
Emission P.
P(CLEAN|R)=0.5
P(CLEAN|S)=0.1
P(SHOPPING|R)=0.4
P(SHOPPING|S)=0.3

11. Transition P.
P(R|START)=0.6
P(S |START)=0.4
P(S|R)=0.3
P(S|S)=0.6
P(R|R)=0.7
P(R|S)=0.4
STATES { R, S}
Emission P.
P(CLEAN|R)=0.5
P(CLEAN|S)=0.1
P(SHOPPING|R)=0.4
P(SHOPPING|S)=0.3
EMISSIONS{CLEAN,SHOPPING}
START S1 S2
CLEAN SHOPPING
START
P(S |START) P(S|S)P(CLEAN|S) P(SHOPPING|S)
P(S |START) P(R|S) P(CLEAN|S) P(SHOPPING|R)
P(R |START) P(S|R) P(CLEAN|R) P(SHOPPING|S)
P(R |START) P(R|R) P(CLEAN|R) P(SHOPPING|R)
ANSWER IS START-RAIN-RAIN

12. Probabilistic Content Model
S1 S2 S3
O1 O3O2
TOPICS
TRANSITIONS
EMISSIONS
SENTENCES

13. Sentences are Bigram Sequences
Probability of a n-word sentence generated from a state s is :

14. Probabilistic Content Model
S1 S2 S3
O1 O3O2
TOPICS
TRANSITIONS
EMISSIONS
SENTENCES

15. TOPICS:
Derived from the content
 Partition sentences from the documents within a domai
n-specific collection into k clusters (Initial Clusters) .
 Use Bigram Vectors as features
 Sentence similarity is the cosine of bigram vectors.
STEP 1

17. An example of the output:
LOCATION INFORMATION

18. TOPICS:
Derived from the content
 D(C,C’): Number of documents in which a sentence from C immediately
precedes one from C’
 D(C): Number of documents containing sentences from C.
 For two States C,C’, smoothed estimate of state transition probability is:

19. EM-like Viterbi Re-estimation
 we can compute the transition probability from the initial sentence clusters (Topic Clusters)
 Hidden Markov Model can estimate the topics of sentences
 Assign sentence s in the topic clusters as the estimated topic.
 Cluster/estimate cycle is repeated until the clusters stabilize
TOPICS:
Derived from the content
STEP 2

20. Evaluation Task 1
Information Ordering
 Information ordering task is essential to many text-
synthesis applications
e.g. concept-to-text generation, multi-document
summarization.

21. Evaluation Task 1
Information Ordering

22. Evaluation Task 1
Information Ordering
Num. of Sentences

23. Evaluation Task 1
Information Ordering
Number of Order of Sentences:
 3 sentences= 3*2*1=6 kinds of different sentence order
 4 sentences =4*3*2*1=24
 Number of sentences over 10 means :
There are over 3 million kinds of different orders .

24. Evaluation Task 1
Information Ordering
 Generate all the sentence orders
 Compute Probability of each order
 Rank the orders by probability
Metric :
 OSO: Original Sentence Order:
Position of Original Sentence in the ranked list
Baseline:
 Word bigram model

25. Evaluation Task 1
Information Ordering
Rank is the Rank of the original sentence order (OSO)
by the model
OSO prediction rate is the percentage of the test
cases in which the model gives highest probability to
the OSO among all possible permutations.

26. Evaluation Task 1
Information Ordering
Indicator of the swaps
•Lapata’ technique is feature-rich method (in this
experiment using linguistic features such as noun-
verb dependency.
•It aggravates the data sparseness problems
for a smaller corpus
Kendall T: measure how much an ordering
differs from the OSO

27. Evaluation Task 2
Summarization
 Baseline: the “Lead” baseline, pick the first L sentences
 Sentence classifer:
1.each sentence is labelled “ in” or “ out” of the summary
2.features for each sentence are unigrams and its location,
which means we look at the words and their location in the
sentences.

28. Evaluation Task 2
Summarization
Probabilistic Content Model:
 All the sentences in the documents are assigned with the topics
 All the sentences in the summaries are assigned with the topics
Probability( Topic A in summary)=
(Number of documents in summary where topic A appears)
(Number of documents in documents where topic A appears )
 Sentences in which its topic has high appearance probability in
summaries are extracted.

29. Evaluation Task 1
Information Ordering
Content Model outperforms sentence-level,
Locally-focused method and L baseline

30. Content model
Word+ Location
baseline

31. Relation Between Two Tasks
Single Domain: Earthquakes
Ordering : OSO prediction rate
Summarization: Extractive accuracy
Optimization of parameters on one task promises to yield good performance on the other
This content model serves as effective representation of text structure in general

32. Conclusions:
In this paper , this unsupervised, knowledge-lean method validates the
hypothesis:
Word distribution patterns strongly correlate with discourse patterns within a
text ( at least specific domains)
Future direction :
This model is a domain-dependent model
Incorporation of domain-independent relations in the transition structure of
the content model.