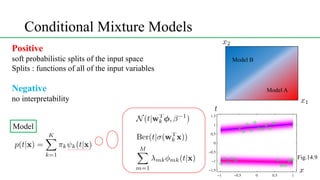
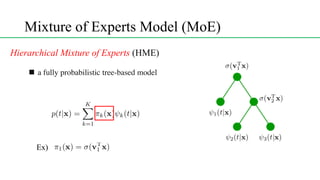
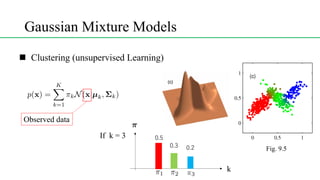
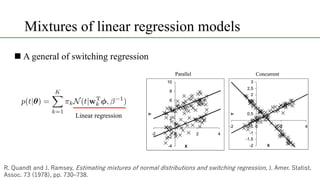
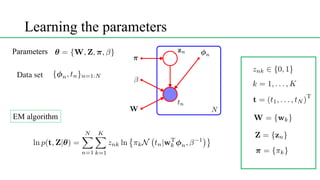
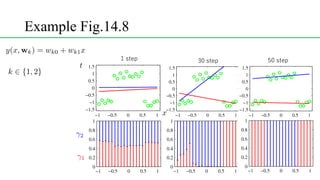
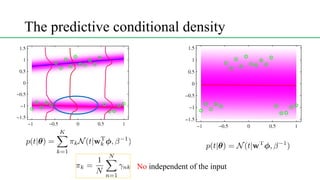
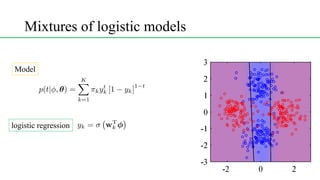
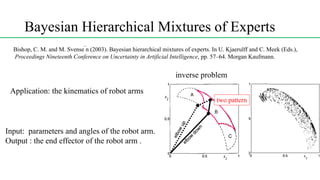
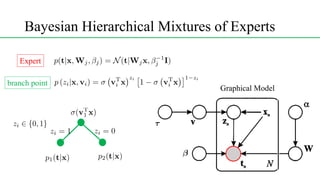
This document discusses conditional mixture models, including mixtures of linear regression models, mixtures of logistic models, and mixtures of experts models. It provides details on learning the parameters of these models using the EM algorithm. Mixtures of experts models use a gating network to determine which expert network is responsible for different regions of the input space. Hierarchical mixtures of experts extend this idea by incorporating multiple levels of gating networks.

1. PRML
14.5 5560 ota

2. Conditional Mixture Models
p14.5.1 Mixtures of linear regression models
p14.5.2 Mixtures of logistic models
p14.5.3 Mixtures of experts

3. Conditional Mixture Models

4. Decision trees
Positive
interpretability
Negative
hard assignment
Splits: axis-aligned of the input space.
Regression:
piecewise-constant predictions
discontinuities at the split boundaries.
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>

5. Conditional Mixture Models
Positive
soft probabilistic splits of the input space
Splits : functions of all of the input variables
Negative
no interpretability
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
Fig.14.9
Model A
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
Model B
Model

6. Mixture of Experts Model (MoE)
<latexit sha1_base64="(null)">(null)</latexit>
n a fully probabilistic tree-based model
Hierarchical Mixture of Experts (HME)
<latexit sha1_base64="(null)">(null)</latexit>
Ex)

7. Mixtures of linear regression models

8. Gaussian Mixture Models
n Clustering (unsupervised Learning)
Fig. 9.5
<latexit sha1_base64="(null)">(null)</latexit>
Observed data
If k = 3
k
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>

9. Mixtures of linear regression models
<latexit sha1_base64="(null)">(null)</latexit>
n A general of switching regression
, 9 3 79 7 97 3 9 8 7 70 7 A7 1 7 3 3 7 )93 . 7
) 1 (
Linear regression

10. Learning the parameters
EM algorithm
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
Parameters
Data set <latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>

11. E step
responsibilities
initialized <latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
The expectation of the complete-data log likelihood

12. M step
Fixed <latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit> <latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
Maximize the function about
the constraint
1) <latexit sha1_base64="(null)">(null)</latexit>
the mixing coefficients
Using a Lagrange multiplier method,

13. M step
2) <latexit sha1_base64="(null)">(null)</latexit>
the parameter of the k-th linear regression model
<latexit sha1_base64="(null)">(null)</latexit>
Linear regression model (3.12)
<latexit sha1_base64="(null)">(null)</latexit>
weighted least squares problem
If k = 3
k
<latexit sha1_base64="(null)">(null)</latexit>
n = 1
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit> <latexit sha1_base64="(null)">(null)</latexit>

14. M step
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
the parameter of the k-th linear regression model
<latexit sha1_base64="(null)">(null)</latexit>
matrix notation
<latexit sha1_base64="(null)">(null)</latexit>
n are learned the data of the high responsibility .<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>

15. M step
a precision parameter<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>

16. Example Fig.14.8
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>

17. The predictive conditional density
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
No independent of the input

18. Mixtures of logistic models

19. Mixtures of logistic models
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
logistic regression
Model

20. Learning the parameters
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
EM algorithm
Parameters
data set <latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
the complete-data log likelihood
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
}

21. E step
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>

22. M step
<latexit sha1_base64="(null)">(null)</latexit>
Fixed <latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
Maximize the function about
<latexit sha1_base64="(null)">(null)</latexit>
the mixing coefficients
}

23. M step
<latexit sha1_base64="(null)">(null)</latexit>
the parameter of the k-th logistic regression model
does not have a closed-form solution.<latexit sha1_base64="(null)">(null)</latexit>
(IRLS) algorithm
<latexit sha1_base64="(null)">(null)</latexit>
n Need the gradient and Hessian
<latexit sha1_base64="(null)">(null)</latexit>

24. IRLS algorithm
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
Gradient
Hessian
<latexit sha1_base64="(null)">(null)</latexit>
While not convergence do
<latexit sha1_base64="(null)">(null)</latexit>

25. A mixture of logistic regression models
true probability of the class label single logistic regression mixture of two logistic regression
<latexit sha1_base64="(null)">(null)</latexit>
Model A
Model B

26. Mixtures of Experts

27. Mixtures of experts
<latexit sha1_base64="(null)">(null)</latexit>
Gating function:
determine which expert are dominant in which region.
be represented by a linear softmax or sigmoid.
n a mixture of experts model
Expert:
can model in different regions of input space.
predict in their own region.
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>

28. Gating function
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
softmaxsigmoid
<latexit sha1_base64="(null)">(null)</latexit>

29. MoE Linear regression model
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
sigmoid
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
MoE
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
Omg!

30. Hierarchical Mixture of Experts
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
HME
Negative
l large number of parameters =>Bayesian HMoE (2003)

31. 5.6 mixture density network
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
output
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
n share the hidden units of the neural network.
n the splits of the input space are relaxed, can be nolinear!
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>

32. Bayesian Hierarchical Mixtures of Experts
Bishop, C. M. and M. Svense ́n (2003). Bayesian hierarchical mixtures of experts. In U. Kjaerulff and C. Meek (Eds.),
Proceedings Nineteenth Conference on Uncertainty in Artificial Intelligence, pp. 57–64. Morgan Kaufmann.
Application: the kinematics of robot arms
inverse problem
two pattern
Input: parameters and angles of the robot arm.
Output : the end effector of the robot arm .

33. Bayesian Hierarchical Mixtures of Experts
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
Expert <latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
Graphical Model
branch point

34. Probabilistic tree-based model
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
: The total number of experts <latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>

35. HMoE Model
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
branch pointExpert
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
Data set
Likelihood

36. Joint probability
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
<latexit sha1_base64="(null)">(null)</latexit>
⇨ Variational Inference

37. fin.