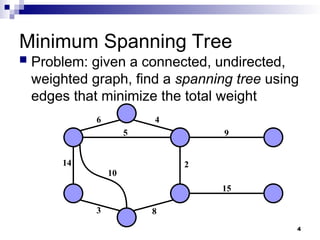
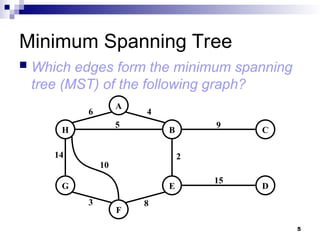
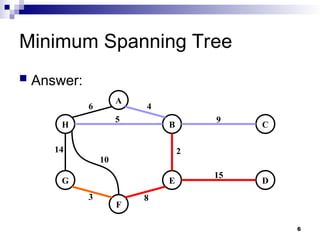
The document explains the concept of Minimum Spanning Trees (MST), detailing the problem of finding a tree in a connected, undirected, weighted graph that minimizes total edge weight. It introduces Prim's algorithm as a method for solving this problem, providing pseudocode and discussing its efficiency in relation to different data structures. Additionally, it raises questions about the algorithm's performance metrics, such as the frequency of operations like extractmin and decreasekey.

1. 1
Minimum Spanning
Tree (MST)
Visit: tshahab.blogspot.com

2. 2
Motivation
For an electrical circuit certain pins have to be grounded.
Finding the arrangement of wires (connecting those pins)
that uses the least amount of wire.
Let a G(V,E) be a graph such that (u, v)  E and a weight
w(u,v) corresponding to wire needed to join u and v.
We are looking for an acyclic subset T  E that connects all
vertices and whose total weight w(T) is minimized.
 
 T
v
u
v
u
w
T
w )
,
(
)
,
(
)
(

3. 3
Motivation
Since T is acyclic and connects all the vertices, it must
form a tree.
Since it spans the graph, it is called a spanning tree.
MST or actually means Minimum Weight Spanning
Tree.

4. 4
Minimum Spanning Tree
 Problem: given a connected, undirected,
weighted graph, find a spanning tree using
edges that minimize the total weight
14
10
3
6 4
5
2
9
15
8

5. 5
Minimum Spanning Tree
 Which edges form the minimum spanning
tree (MST) of the following graph?
H B C
G E D
F
A
14
10
3
6 4
5
2
9
15
8

6. 6
Minimum Spanning Tree
 Answer:
H B C
G E D
F
A
14
10
3
6 4
5
2
9
15
8

7. 7
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);

8. 8
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
14
10
3
6 4
5
2
9
15
8
Run on example graph

9. 9
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
  
  


14
10
3
6 4
5
2
9
15
8
Run on example graph

10. 10
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
  
0  


14
10
3
6 4
5
2
9
15
8
Pick a start vertex r
r

11. 11
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
  
0  


14
10
3
6 4
5
2
9
15
8
Black vertices have been removed from Q
u

12. 12
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
  
0  
3

14
10
3
6 4
5
2
9
15
8
Black arrows indicate parent pointers
u

13. 13
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
14  
0  
3

14
10
3
6 4
5
2
9
15
8
u

14. 14
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
14  
0  
3

14
10
3
6 4
5
2
9
15
8
u

15. 15
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
14  
0 8 
3

14
10
3
6 4
5
2
9
15
8
u

16. 16
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
10  
0 8 
3

14
10
3
6 4
5
2
9
15
8
u

17. 17
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
10  
0 8 
3

14
10
3
6 4
5
2
9
15
8
u

18. 18
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
10 2 
0 8 
3

14
10
3
6 4
5
2
9
15
8
u

19. 19
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
10 2 
0 8 15
3

14
10
3
6 4
5
2
9
15
8
u

20. 20
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
10 2 
0 8 15
3

14
10
3
6 4
5
2
9
15
8
u

21. 21
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
10 2 
0 8 15
3
4
14
10
3
6 4
5
2
9
15
8
u

22. 22
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
5 2 
0 8 15
3
4
14
10
3
6 4
5
2
9
15
8
u

23. 23
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
5 2 9
0 8 15
3
4
14
10
3
6 4
5
2
9
15
8
u

24. 24
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
5 2 9
0 8 15
3
4
14
10
3
6 4
5
2
9
15
8
u

25. 25
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
5 2 9
0 8 15
3
4
14
10
3
6 4
5
2
9
15
8
u

26. 26
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
5 2 9
0 8 15
3
4
14
10
3
6 4
5
2
9
15
8
u

27. 27
Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
5 2 9
0 8 15
3
4
14
10
3
6 4
5
2
9
15
8
u

28. 28
Review: Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
What is the hidden cost in this code?

29. 29
Review: Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
DecreaseKey(v, w(u,v));

30. 30
Review: Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
DecreaseKey(v, w(u,v));
How often is ExtractMin() called?
How often is DecreaseKey() called?

31. 31
Review: Prim’s Algorithm
MST-Prim(G, w, r)
Q = V[G];
for each u  Q
key[u] = ;
key[r] = 0;
p[r] = NULL;
while (Q not empty)
u = ExtractMin(Q);
for each v  Adj[u]
if (v  Q and w(u,v) < key[v])
p[v] = u;
key[v] = w(u,v);
What will be the running time?
A: Depends on queue
binary heap: O(E lg V)
Fibonacci heap: O(V lg V + E)