Downloaded 20 times
![Defining Equation of Time
So the equation of time at any instant at a given place
is defined as the difference between the apparent
solar time and mean solar time at that instant.
Equation of time = Apparent solar time – Mean solar
time
= H.A. of apparent sun – H.A. of mean
sun
= R.A. of mean sun – R.A. of apparent
sun
Since, H.A. of a body = – R. A. of the body .
[H.A. = Hour Angle
R.A. = Right Ascension]
© Department of Mathematics, R.U.](https://image.slidesharecdn.com/5f32ca26-6ea7-4841-8941-24bdc6d491cc-161026103018/85/Presentation-on-Equation-of-time-11-320.jpg)
Uploaded byMd. Nazmus Saqib Khan
Presentation on Equation of time
The document is a presentation on the equation of time. It begins by defining key terms like apparent sun, mean sun, apparent solar time, and mean solar time. It then defines the equation of time as the difference between apparent and mean solar time, which can range from -14 to +16 minutes. The chief causes of this difference are the unequal speed of the earth in its orbit and the fact that the apparent sun is on the ecliptic while the mean sun is on the equator. Graphs and tables are shown to represent the equation of time. Finally, some applications are discussed, such as correcting sundial times and accounting for the equation of time in solar energy systems.
More Related Content
Similar to Presentation on Equation of time
Presentation on Equation of time
- 1. Presentation on Equation ofTime Presented By: Md. Nazmus Saqib Khan ID 12075768 Year: 4th Session: 2011-12 Department of Mathematics University of Rajshahi-6205
- 2. Index Some Definitions Defining Equationof Time Chief Causes of Equation of Time Graphical Representation Some applications References © Department of Mathematics, R.U.
- 3. Some Definitions Apparent sun Meansun Apparent solar time Mean solar time Transit Hour Angle Right Ascension © Department of Mathematics, R.U.
- 4. Some Definitions © Departmentof Mathematics, R.U. Apparent sun: The sun we see in the sky is called apparent sun. Mean sun: The mean sun is fictitious point which moves uniformly along the equator with the mean velocity of the sun along the ecliptic.
- 5. Some Definitions Apparent SolarTime: Apparent solar time at any instant is the time that has elapsed since the preceding apparent midnight. Apparent midnight is the instant of the sun’s lower transit on the meridian. Apparent solar time is equal to the hour angle of the apparent sun. It is actually the time shown by a sundial. (Fig.1) Fig.1: Roman Sundial© Department of Mathematics, R.U.
- 6. Some Definitions Mean SolarTime: The mean solar time at any instant is the time that has elapsed since the lower transit of the mean sun. In other words, the time indicated by the mean sun is termed as mean solar time or simply mean time. Mean solar time is equal to the hour angle of the mean sun. It is actually our clock time. (Fig.2) Fig.2: Mechanical Clock © Department of Mathematics, R.U.
- 7. Some Definitions Transit: Theinstant when any point on the celestial sphere is on the meridian of an observer is called the transit or culmination, of that point over that meridian. When it is on the half of the meridian containing the zenith is called upper transit; when it is on the other half it is called lower transit.(Fig.3) Fig.3: Transit © Department of Mathematics, R.U.
- 8. Some Definitions Hour Angle:It is the angle subtended at the pole between the observer’s meridian and the hour circle of the body. In the northern hemisphere, the hour angle is always measured from the south towards the west upto the hour circle of the heavenly body. (Fig.4) Fig.4: Hour angle © Department of Mathematics, R.U.
- 9. Some Definitions Right ascension:It is the angular distance measured from the vernal equinox along the equator to the point of intersection of the equator with the hour circle through the body. It is measured from the vernal equinox eastwards from 0 to 360 degrees. (Fig.5) Fig.5: Right Ascension © Department of Mathematics, R.U.
- 10. Defining Equation ofTime Since observations made on the sun for the purpose of determining the time can give apparent time only, it is necessary to be able to find at any instant the exact relation between apparent and mean time. The difference between the two, which varies from -14m to +16m (nearly), is called the equation of time. This quantity may be found in the Nautical Almanac for each day of the year. © Department of Mathematics, R.U.
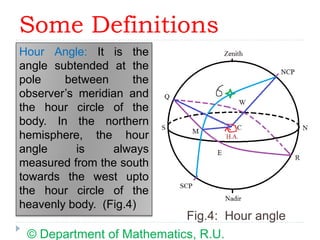
- 11. Defining Equation ofTime So the equation of time at any instant at a given place is defined as the difference between the apparent solar time and mean solar time at that instant. Equation of time = Apparent solar time – Mean solar time = H.A. of apparent sun – H.A. of mean sun = R.A. of mean sun – R.A. of apparent sun Since, H.A. of a body = – R. A. of the body . [H.A. = Hour Angle R.A. = Right Ascension] © Department of Mathematics, R.U.
- 12. Chief Causes ofEquation of Time The difference between the two kinds of time is due to several causes, the chief of which are: I. The inequality of the earth’s angular motion in the orbit, and II. The fact that the apparent sun is on the ecliptic while the mean sun is on the equator. © Department of Mathematics, R.U.
- 13. Graphical Representation Table A.Equation of Time for 1910 © Department of Mathematics, R.U.
- 14. Graphical Representation Fig. 6:Graphical representation of Equation of Tim © Department of Mathematics, R.U.
- 15. Some applications Theequation of time is used to correct the sundial time. In the late 17th and 18th centuries, equation clocks were made, which allowed the user to see or calculate apparent solar time, as would be shown by a sundial. It is also used for many applications of solar energy. Machines such as solar trackers and heliostats have to move in ways that are influenced by the equation of time. Civil time is the local mean time for a meridian that often passes near the center of the time zone, and may possibly be further altered by daylight saving time. When the apparent solar time that corresponds to a given civil time is to be found, the difference in longitude between the site of interest and the time zone meridian, daylight saving time, and the equation of time must all be considered. © Department of Mathematics, R.U.
- 16. Some applications Fig.7: 8MWHorizontal Single Axis Tracker in Greece © Department of Mathematics, R.U.
- 17. Some applications Fig. 8:Heliostat by the Viennese instrument maker Ekling (ca. 1850) © Department of Mathematics, R.U.
- 18. Some applications Fig. 9:Standard Time Zone of the World © Department of Mathematics, R.U.
- 19. References Spherical Astronomyby W. M. Smart Practical Astronomy by George L. Hosmer Spherical Astronomy by Sharma Astronomy by K. K. De The Astronomical Almanac online Wikipedia Google Images © Department of Mathematics, R.U.
- 20. END OF THISPRESENTATION Any Questions? Thank You! © Department of Mathematics, R.U.