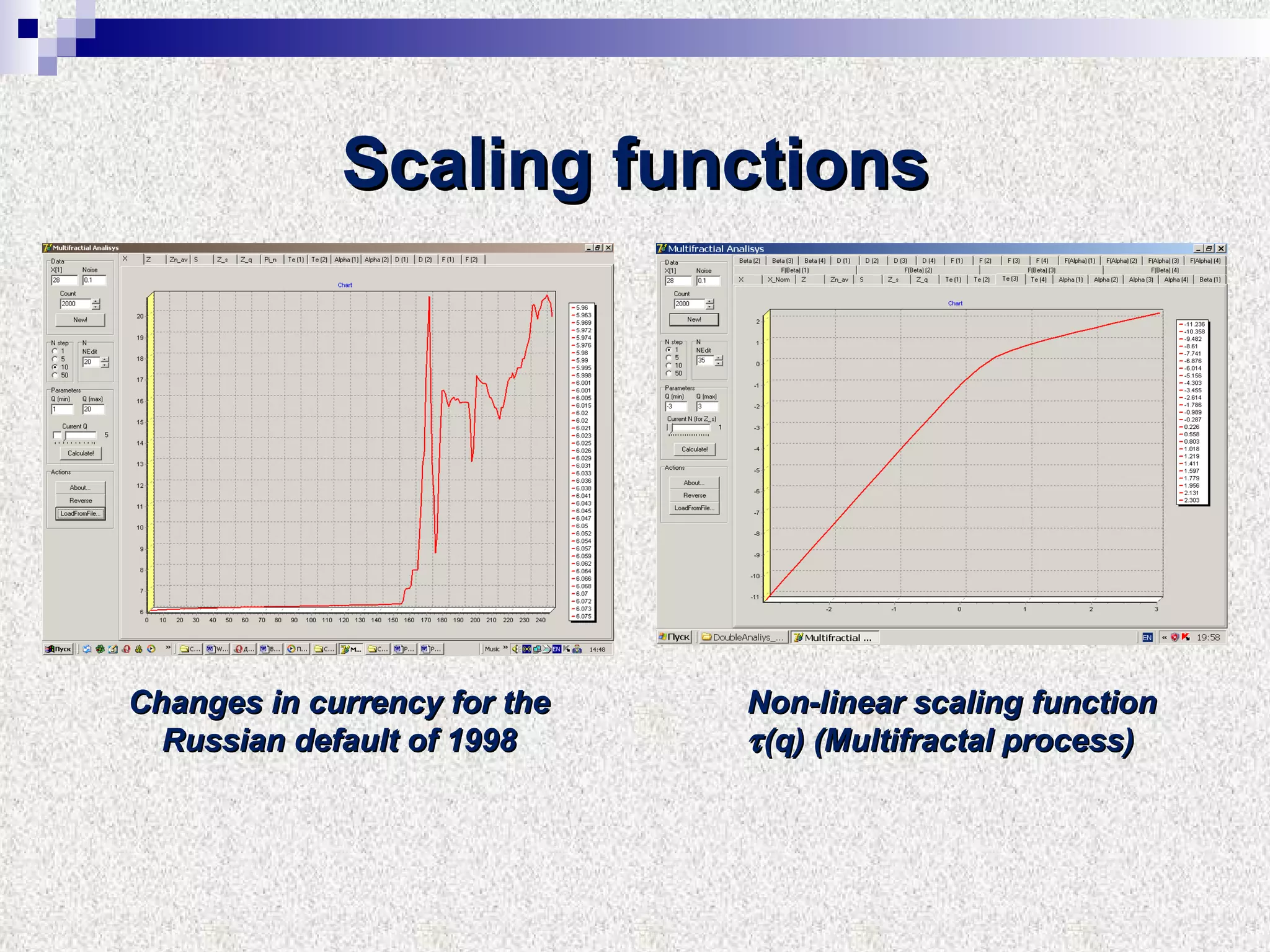
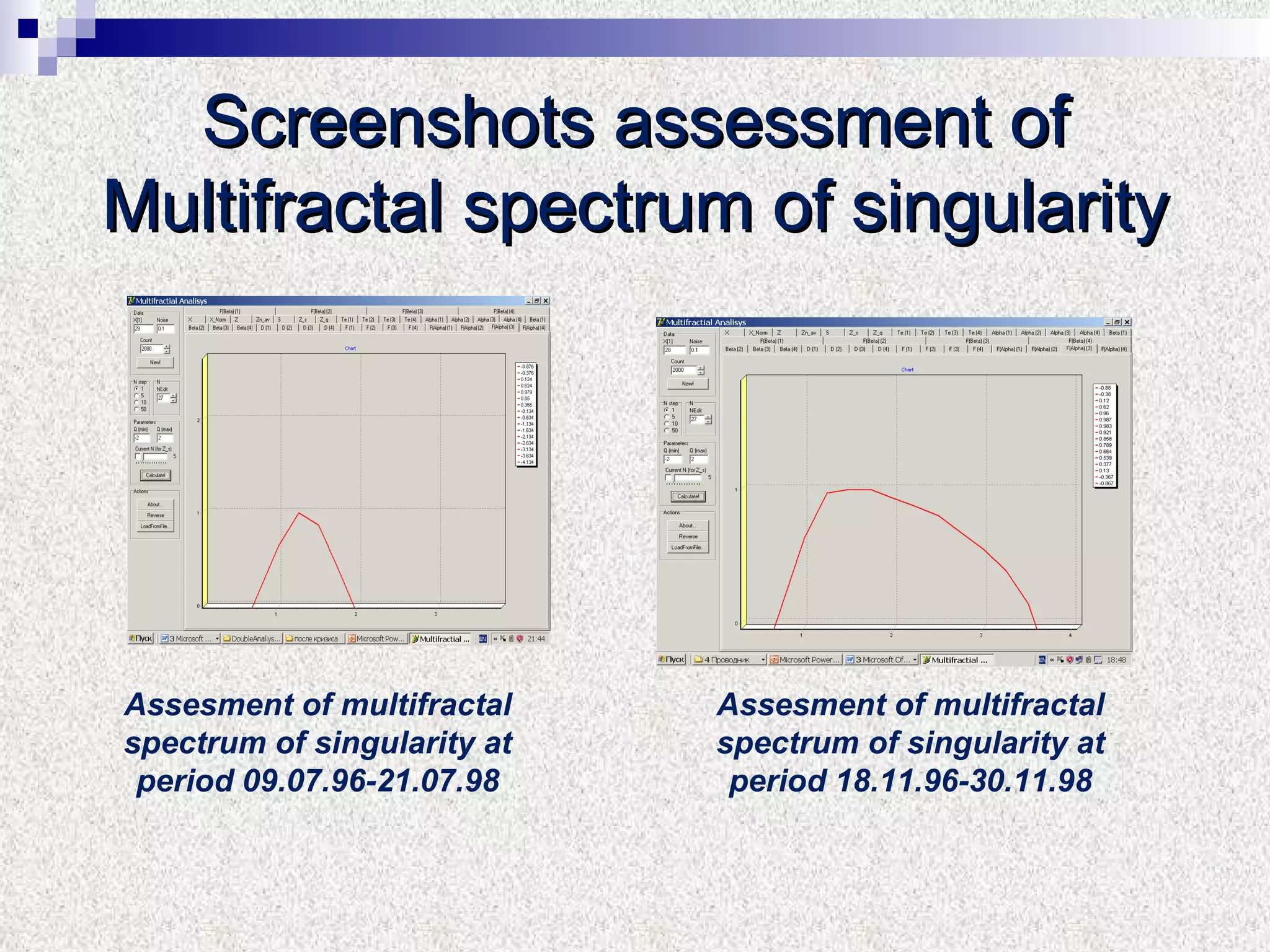
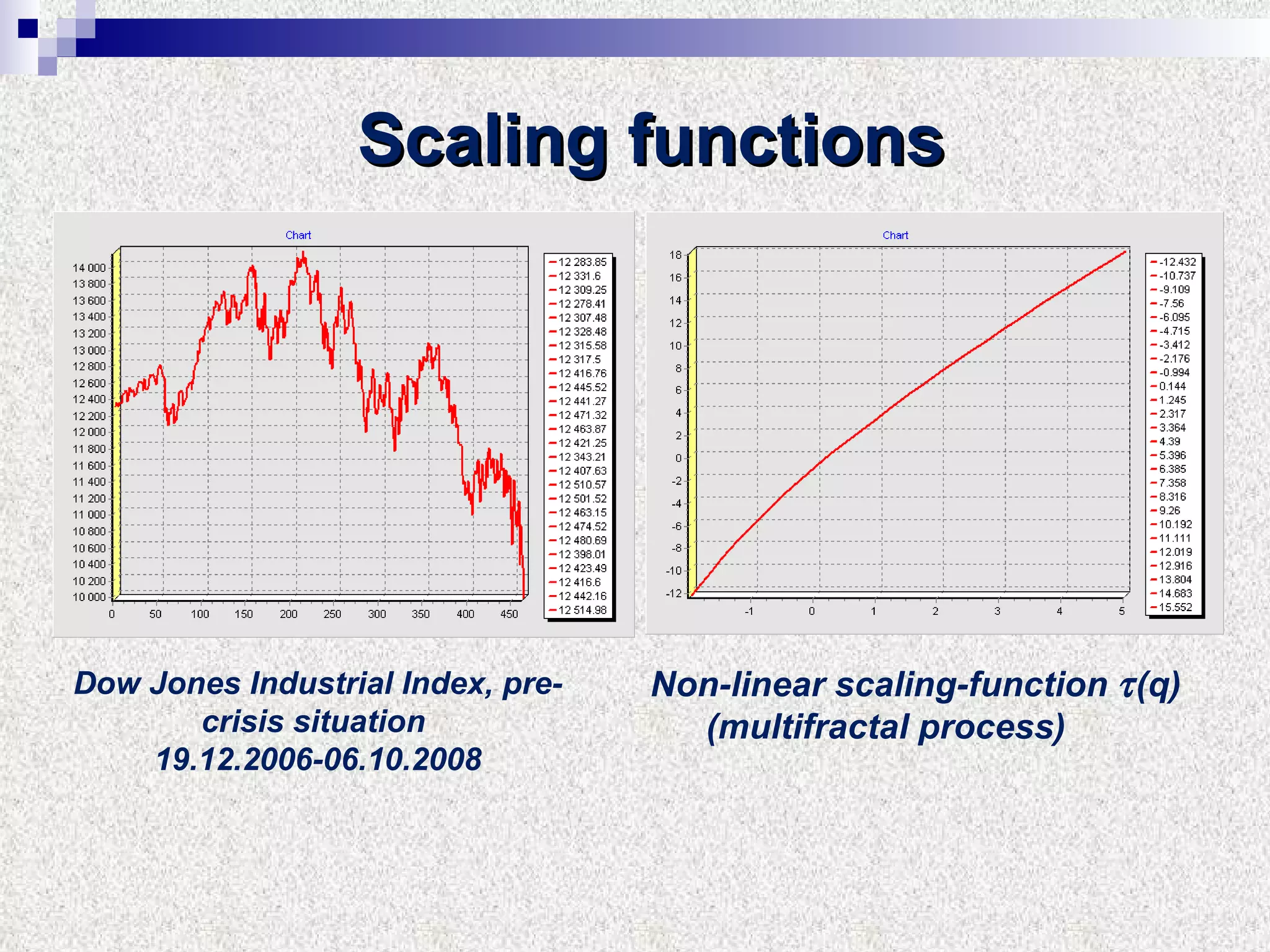
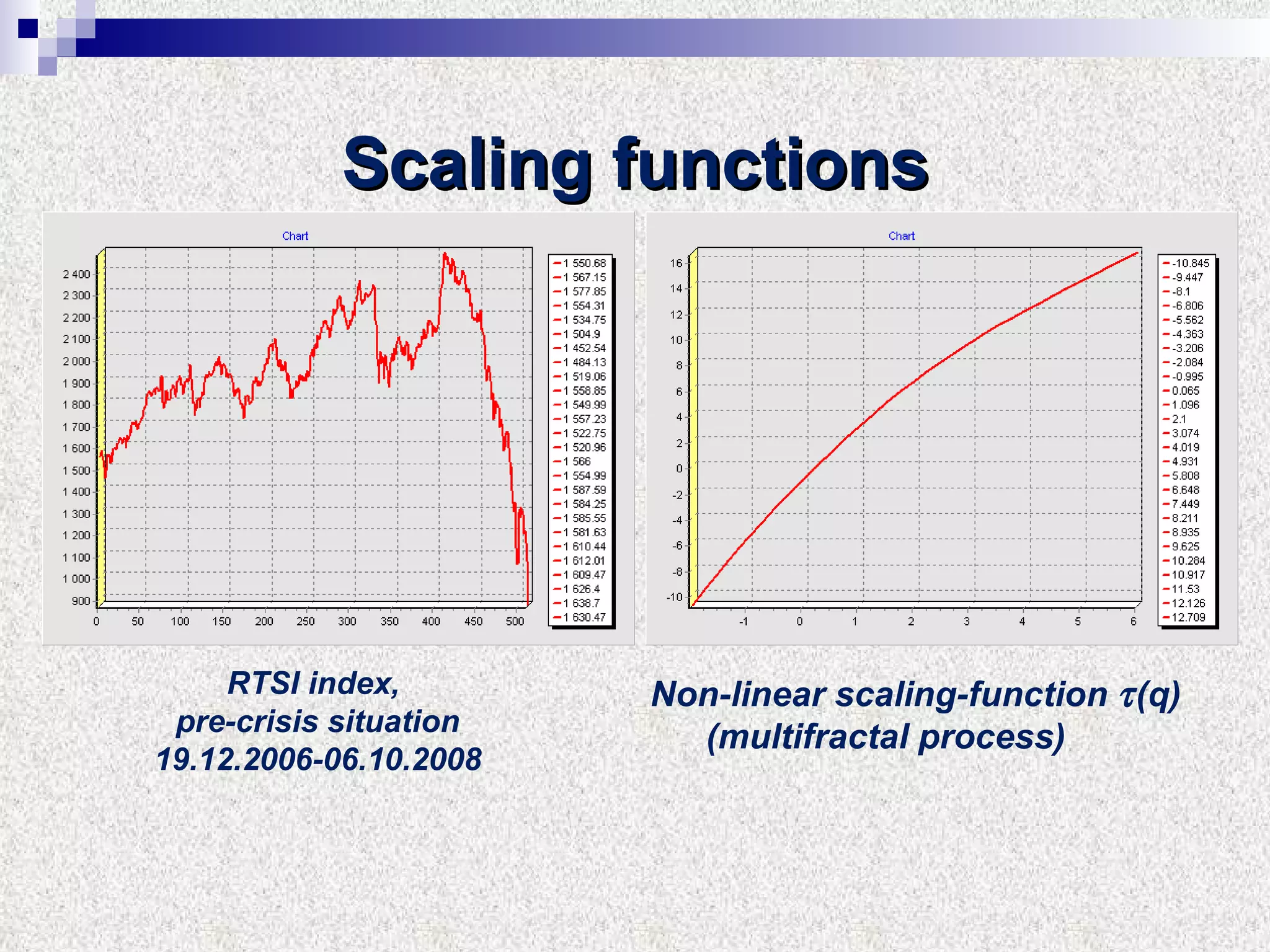
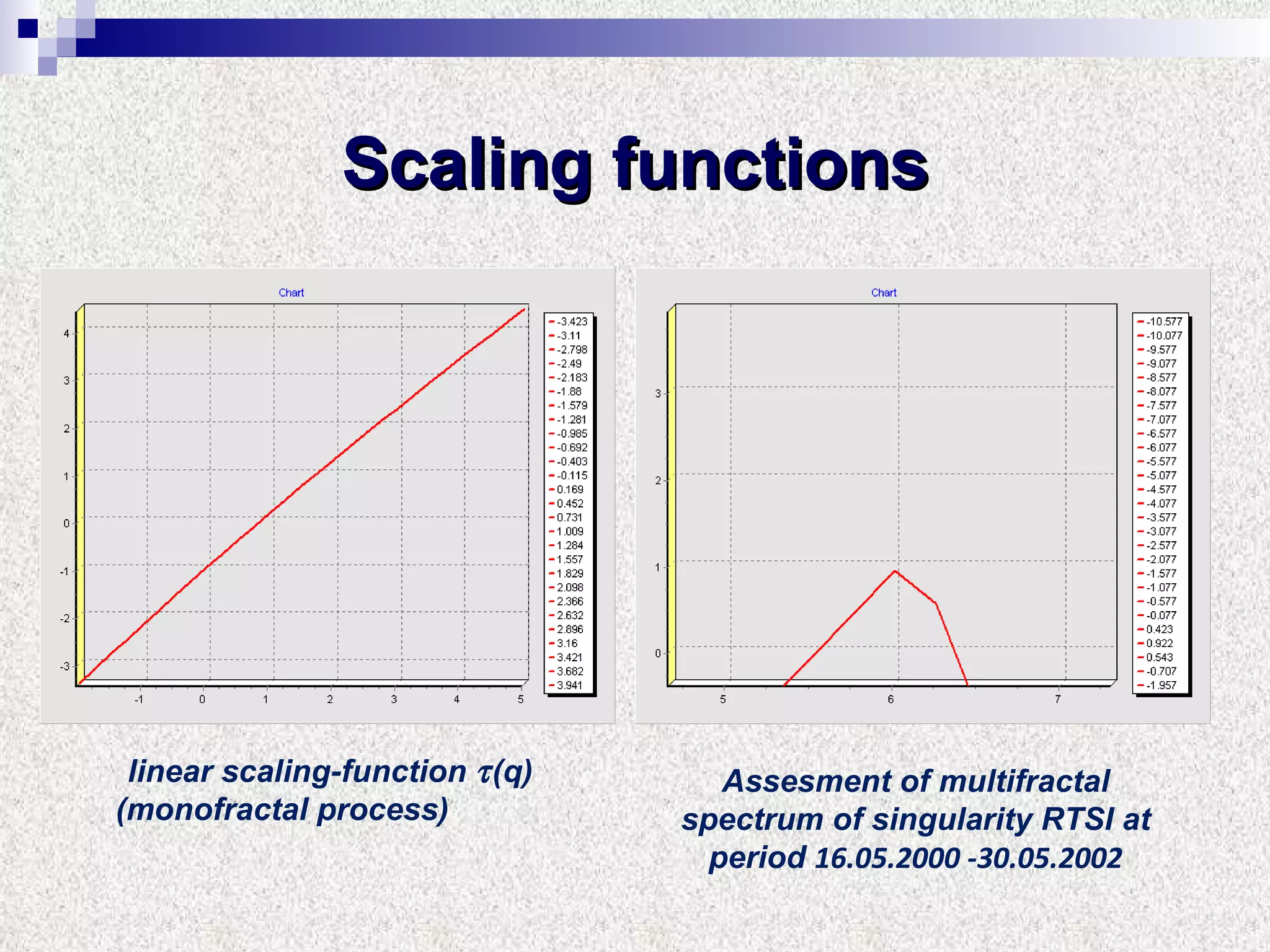
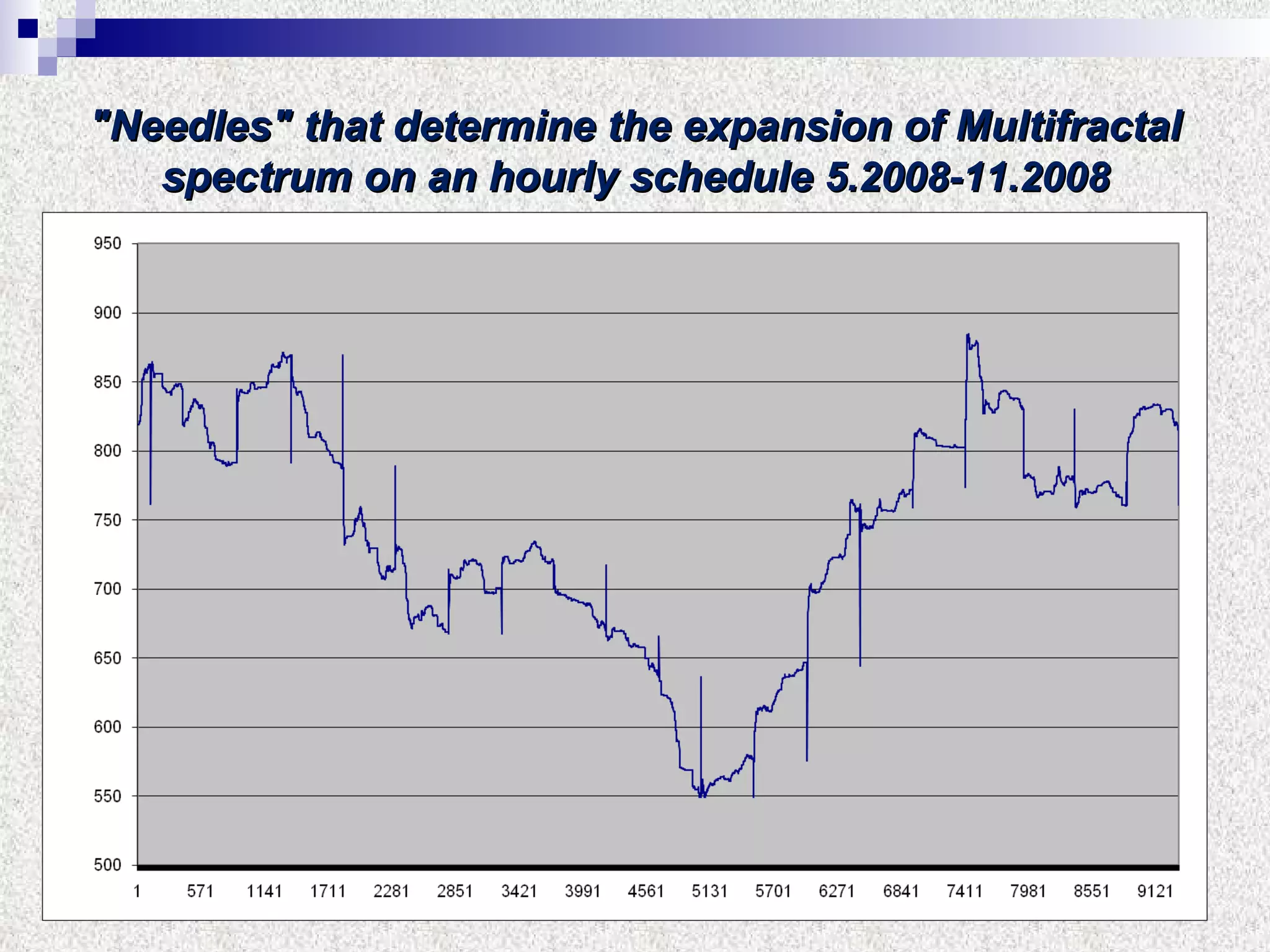
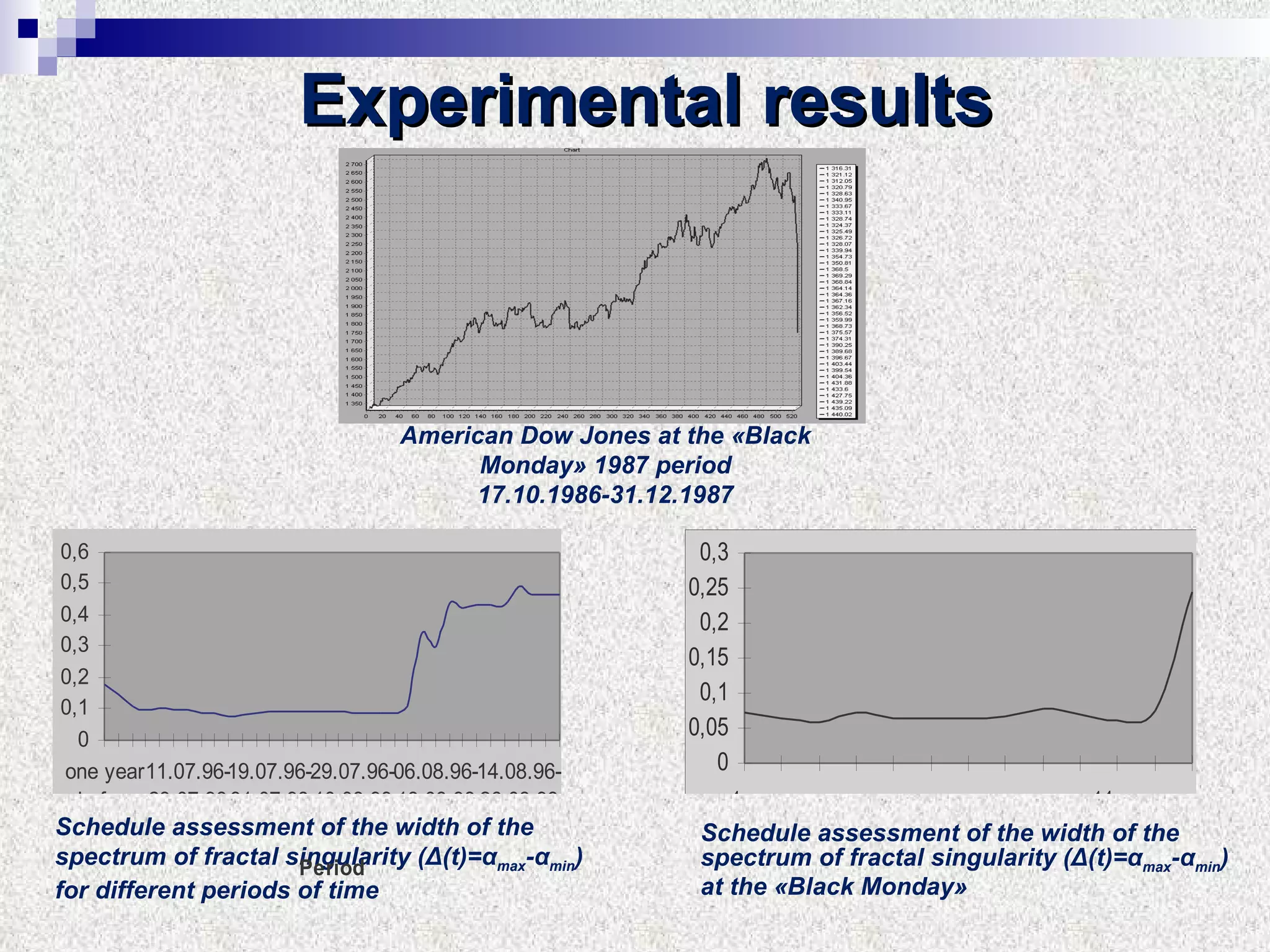
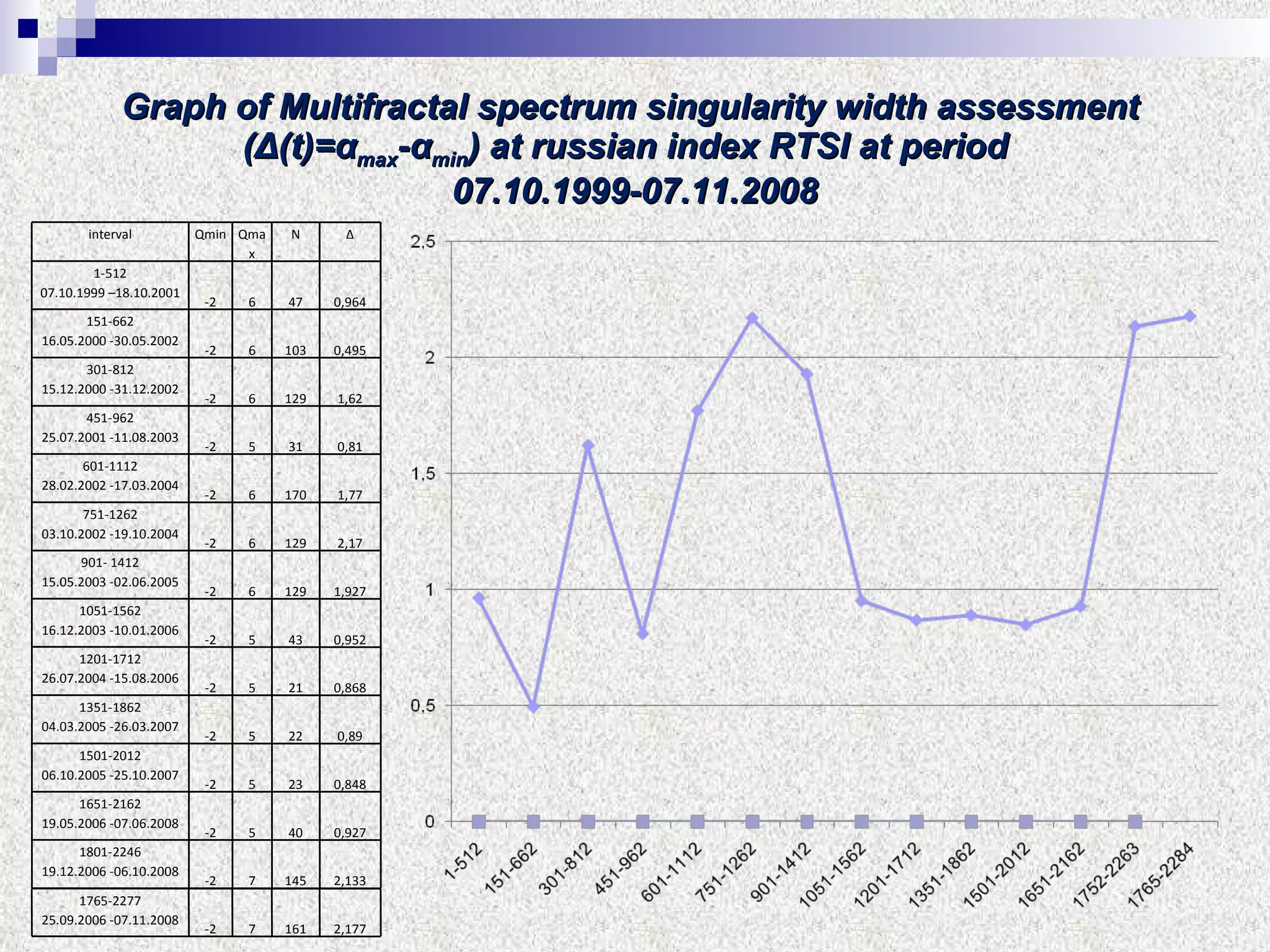
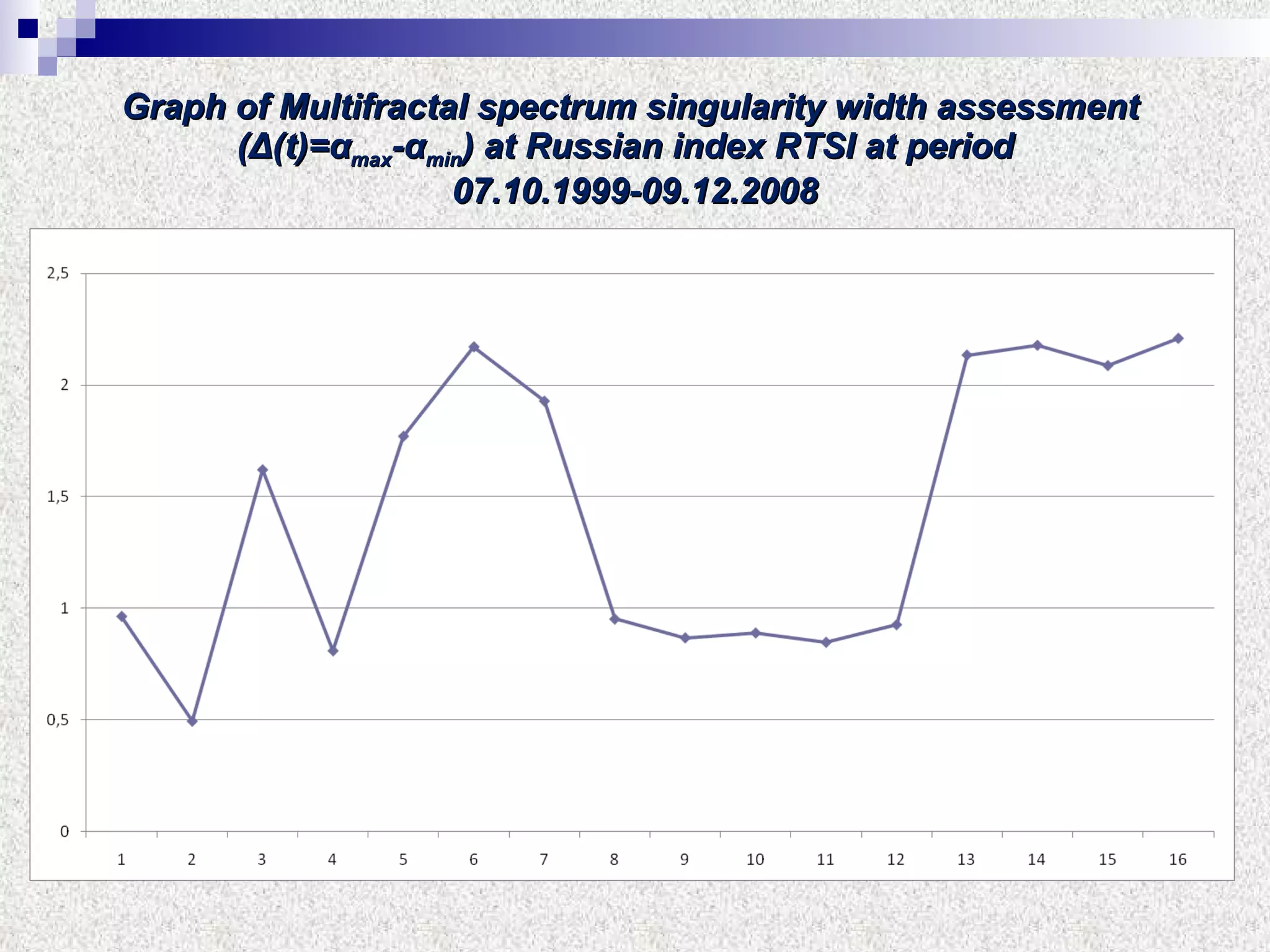
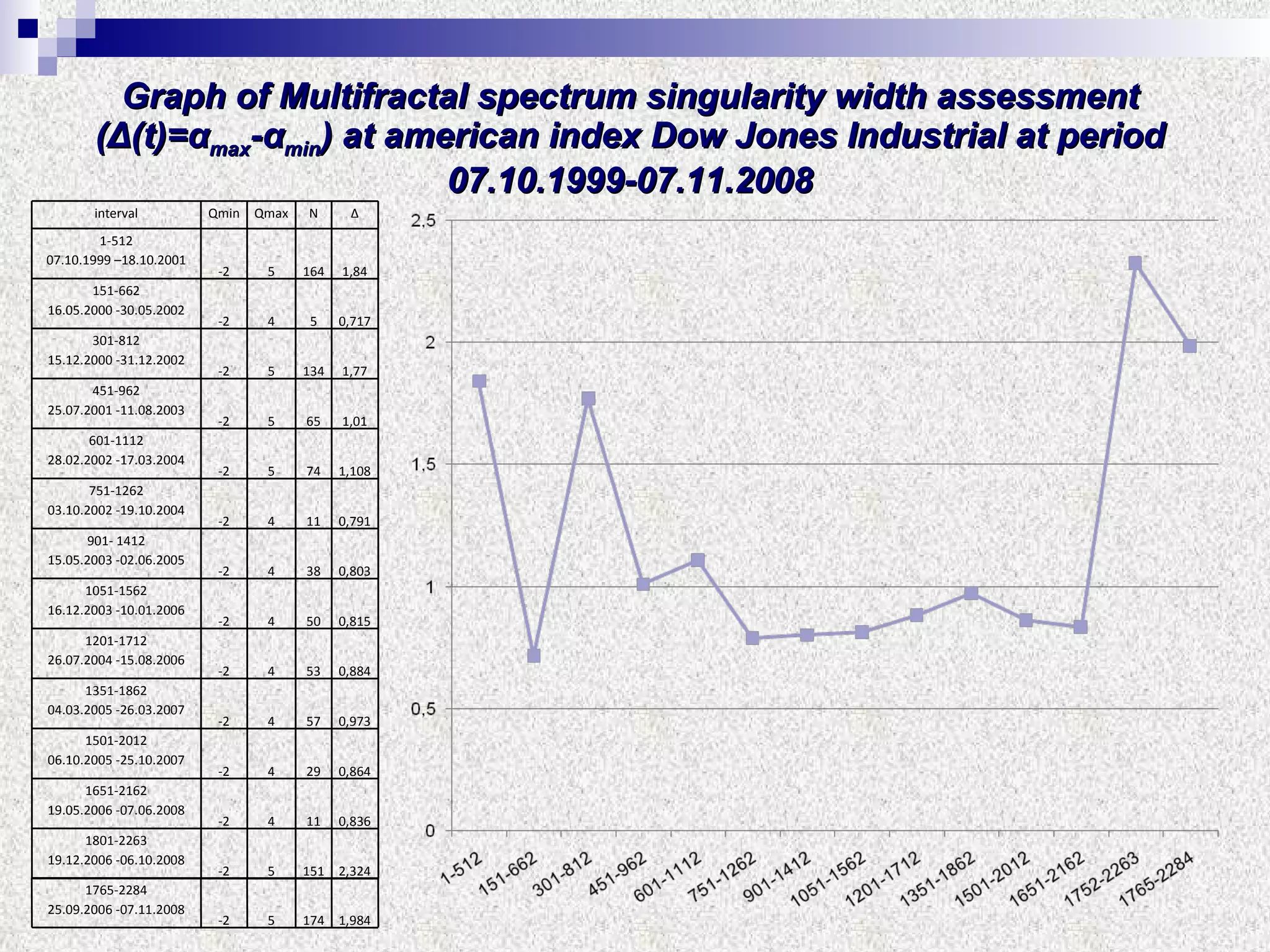
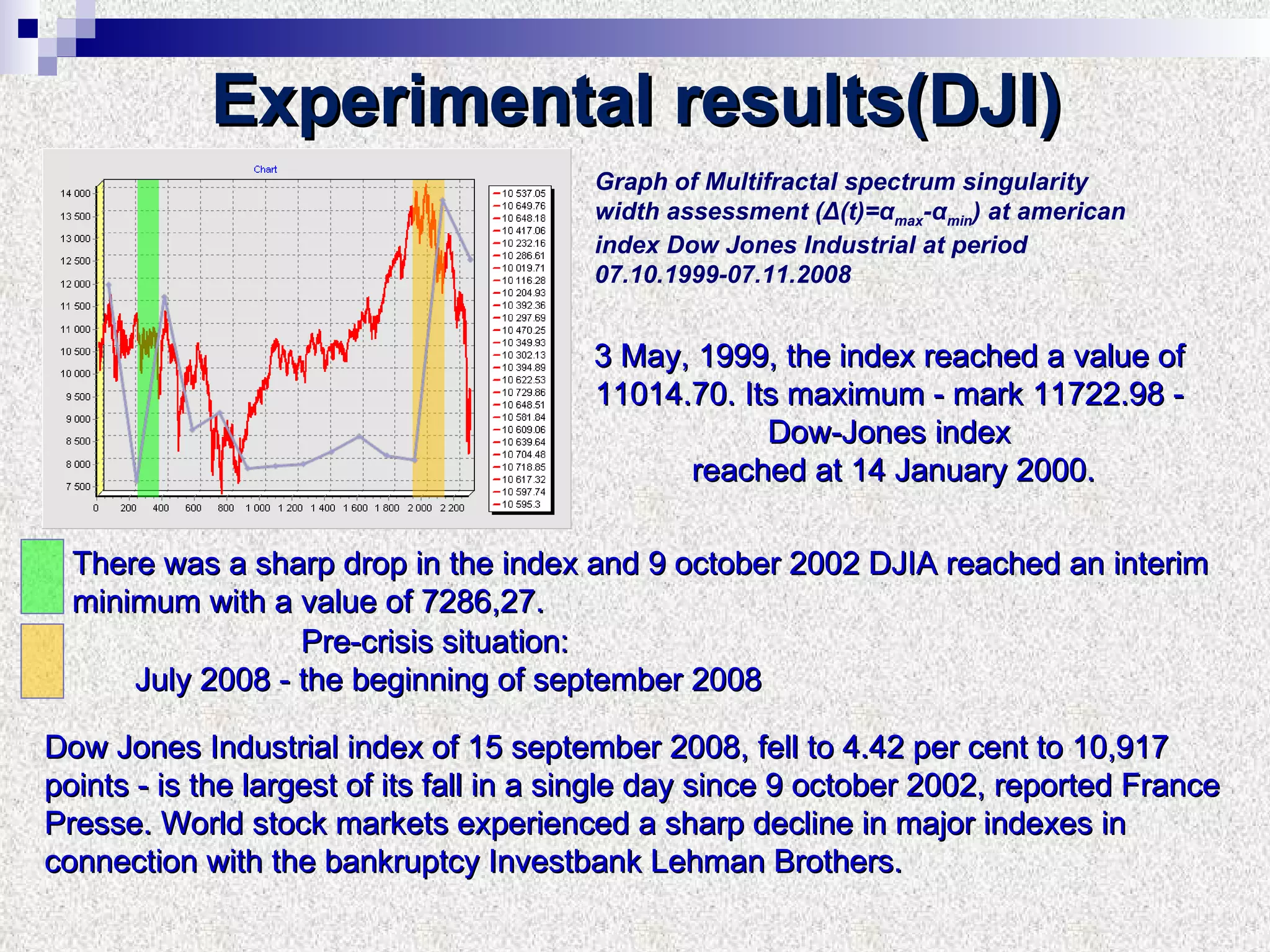
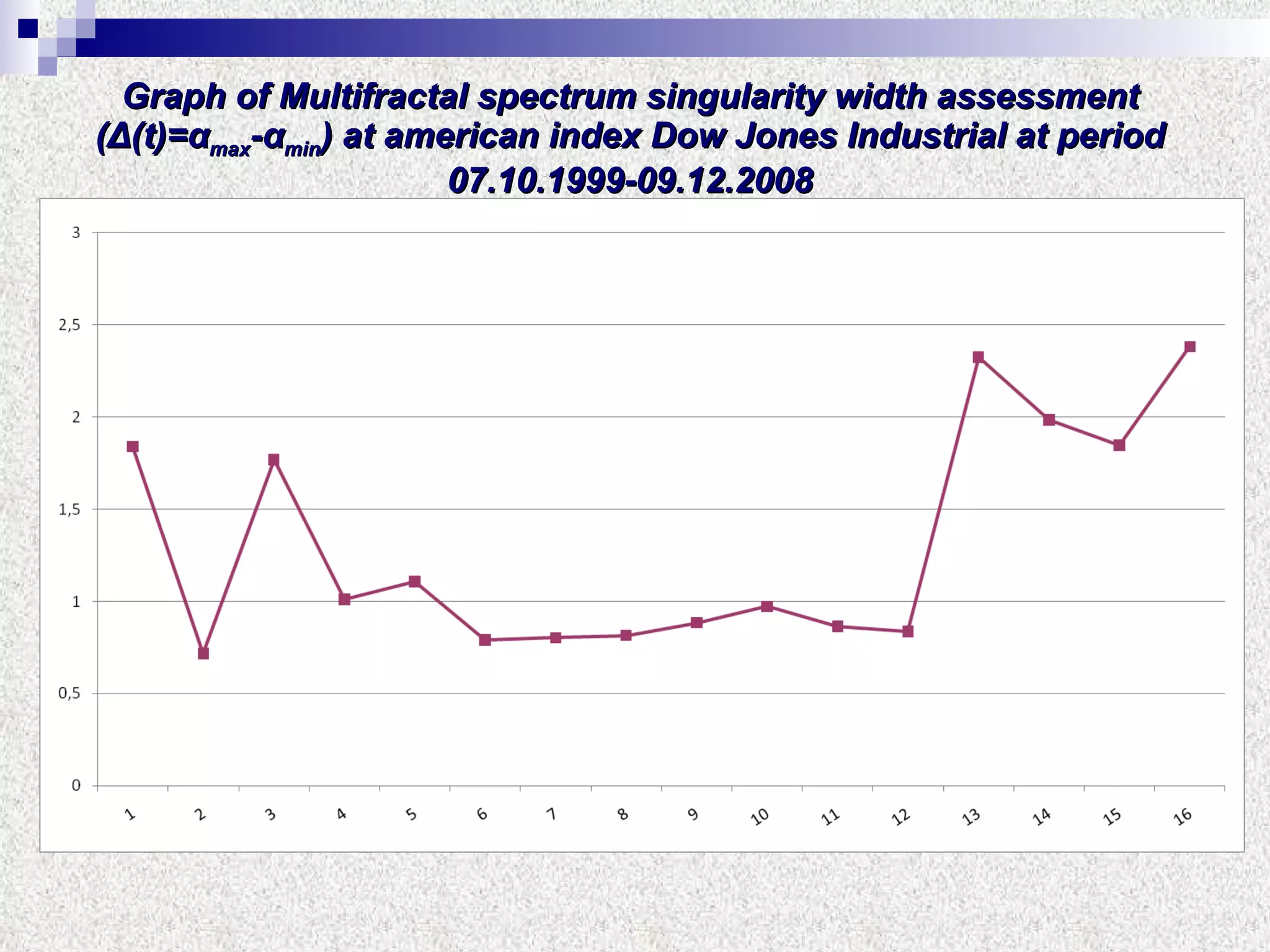
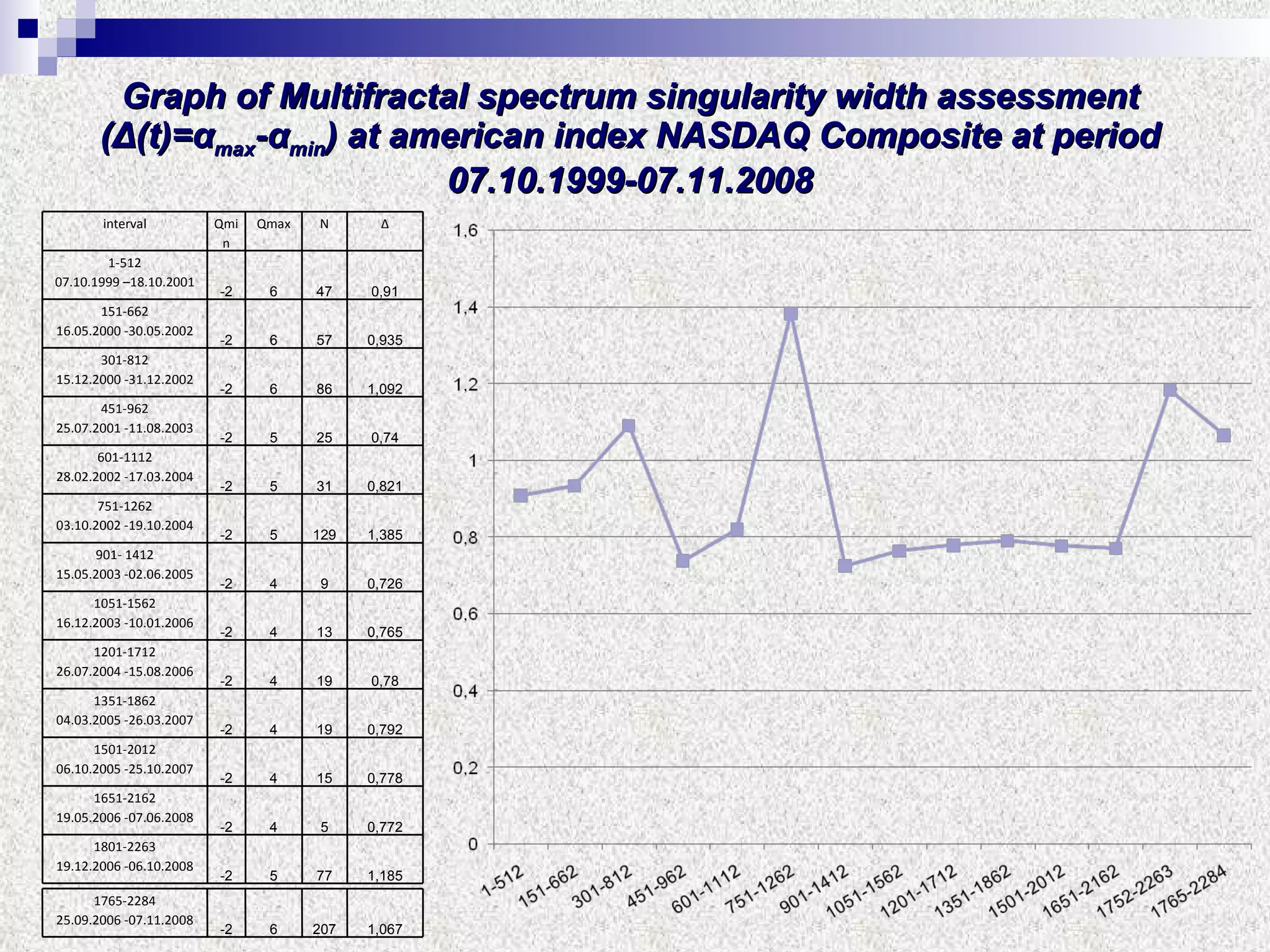
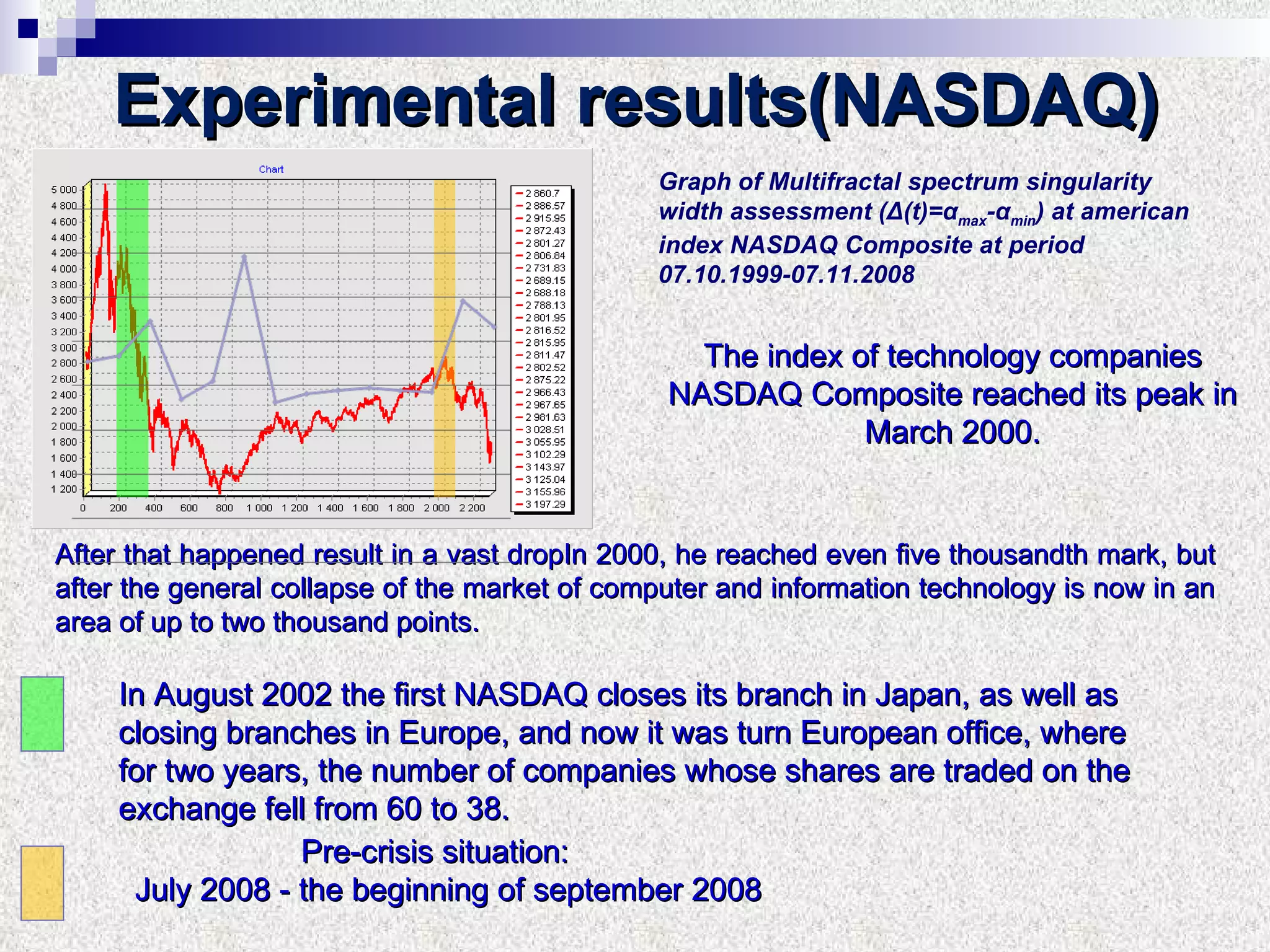
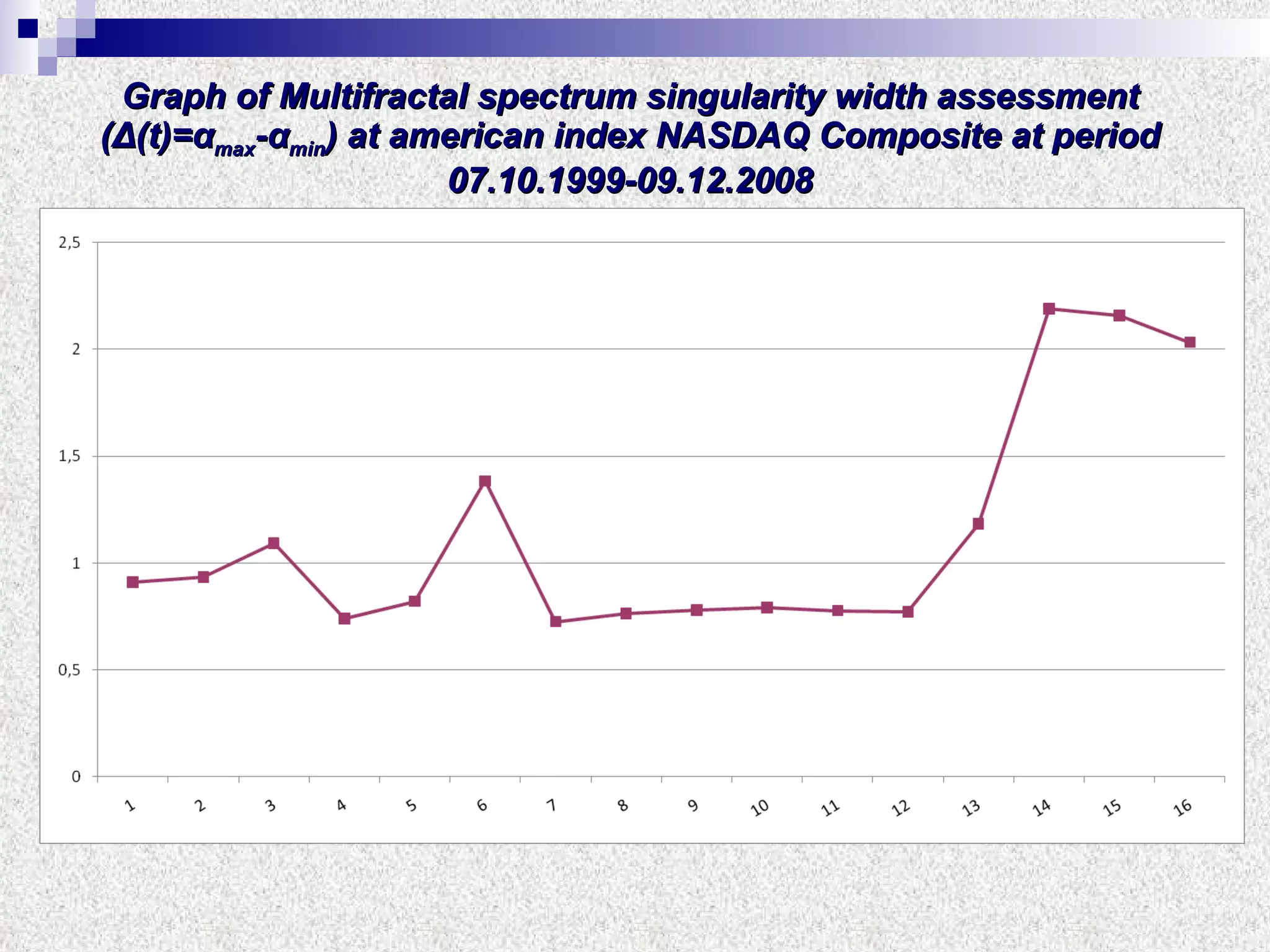
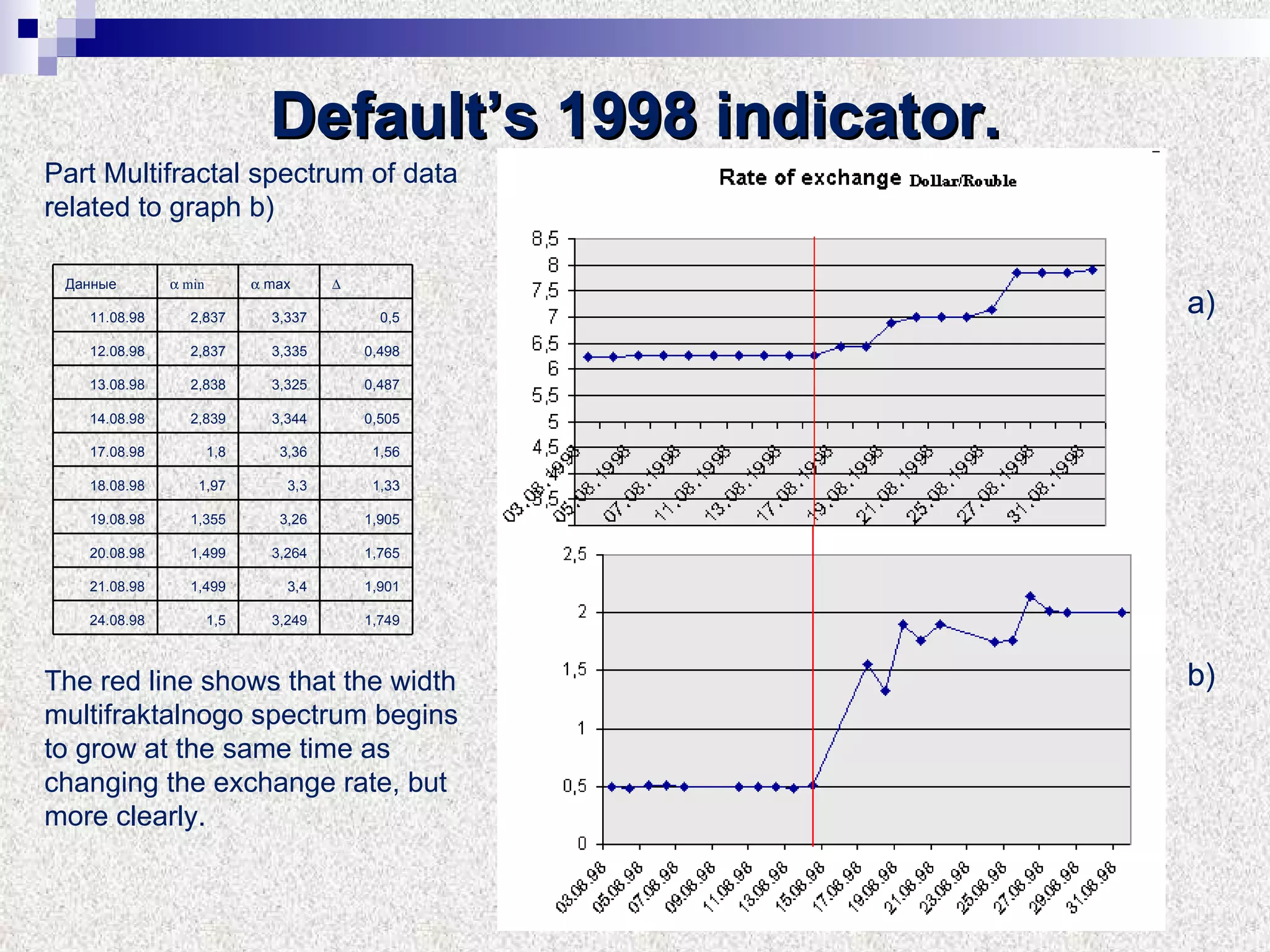
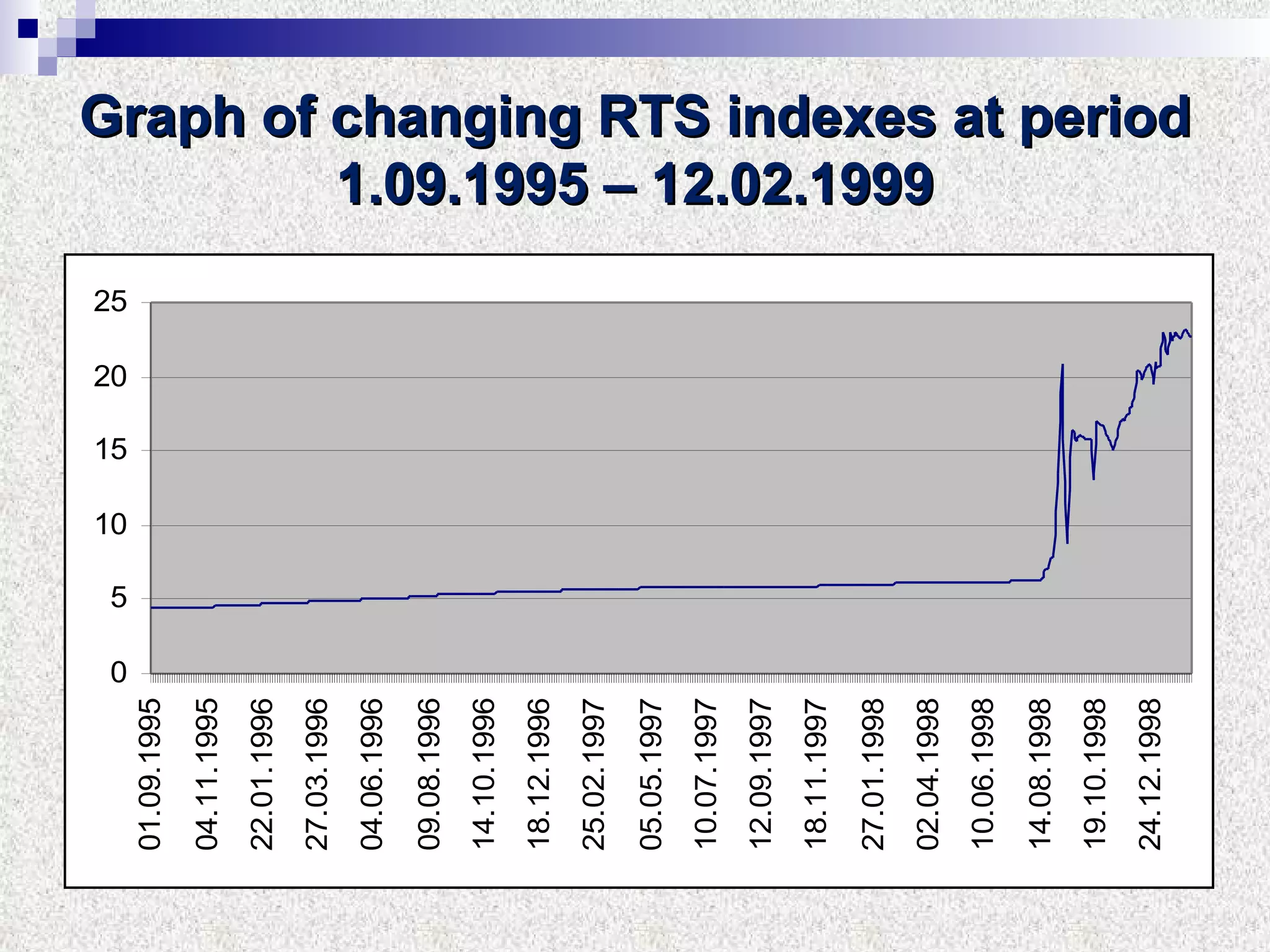
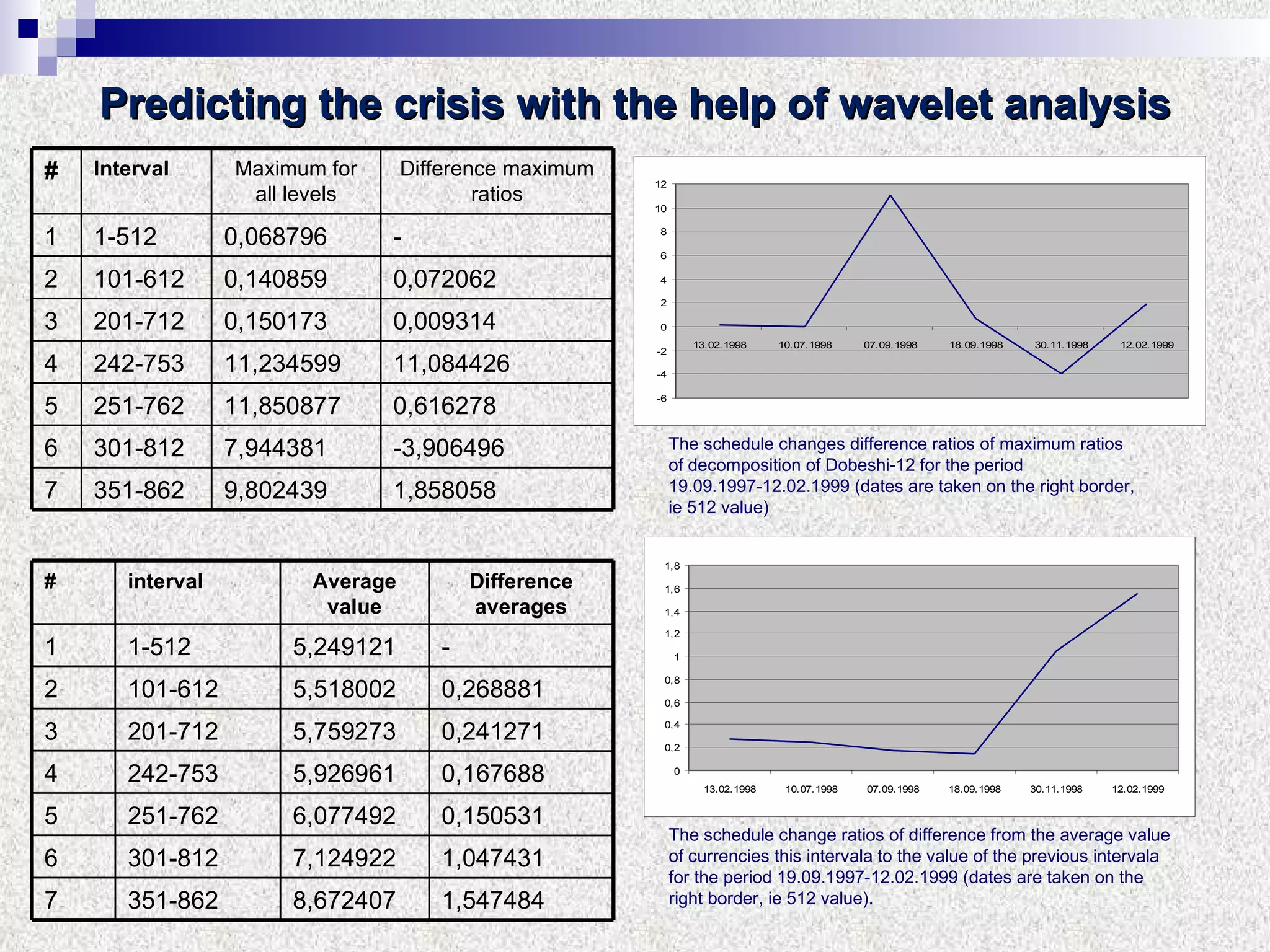
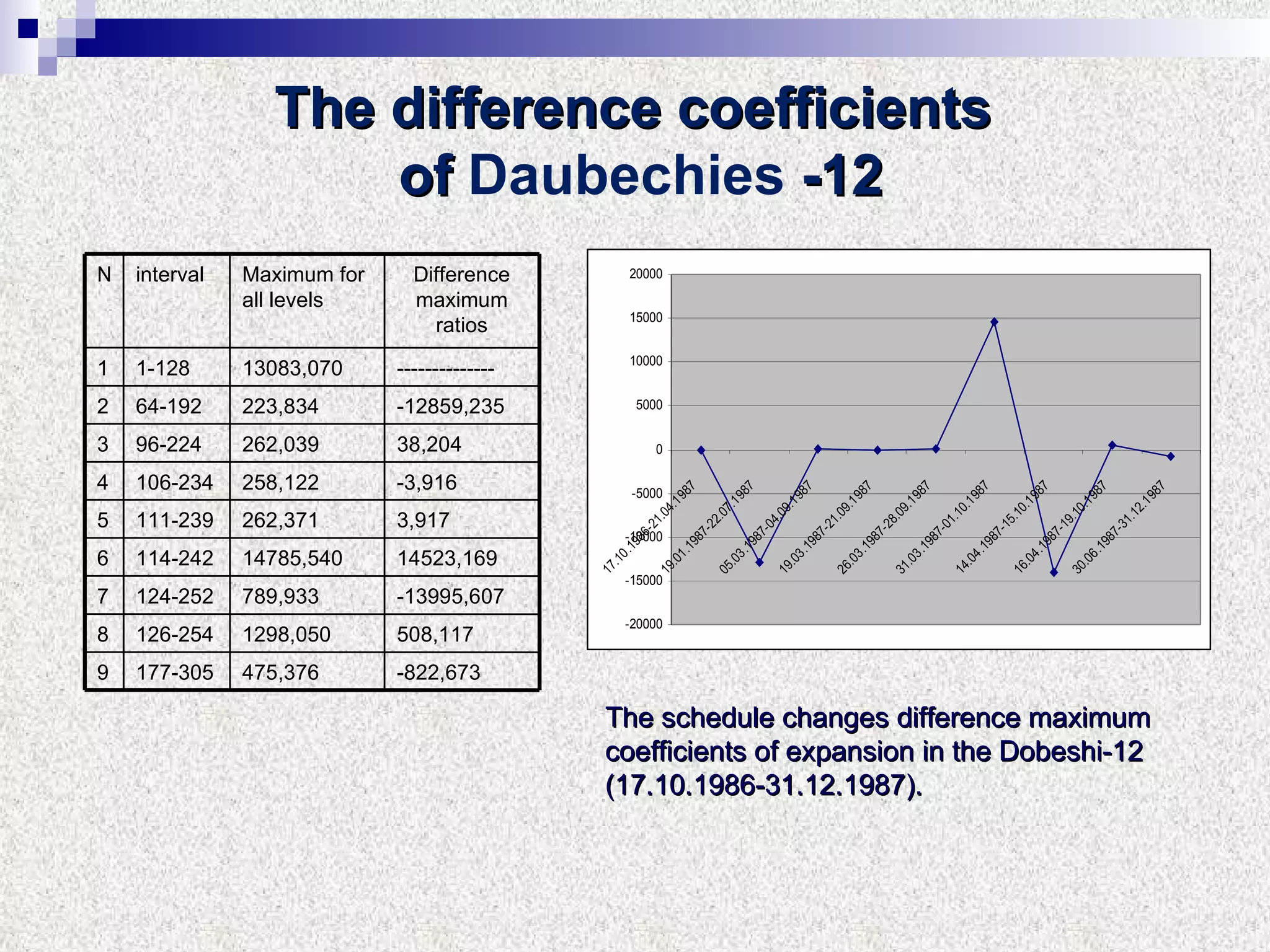
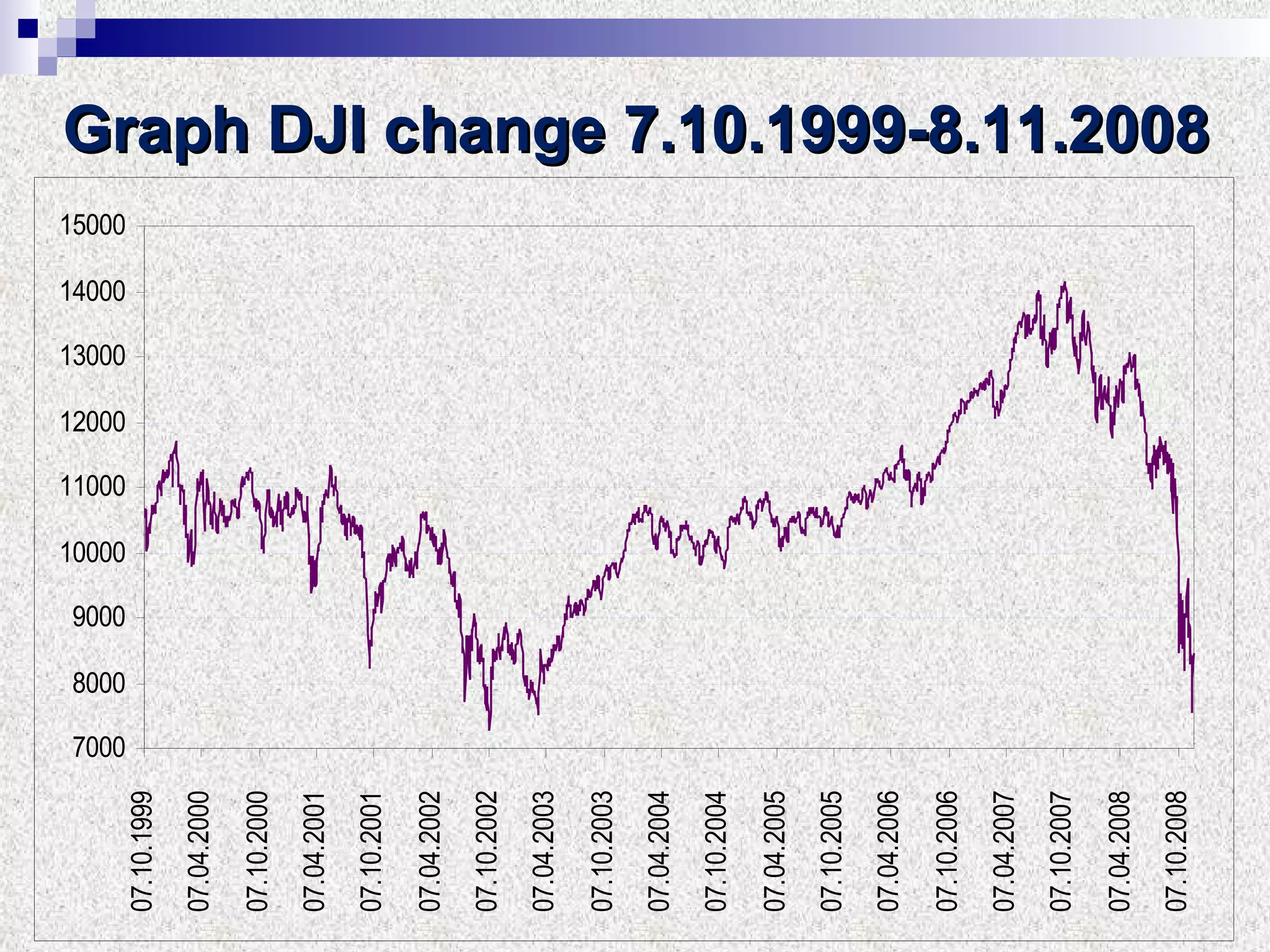
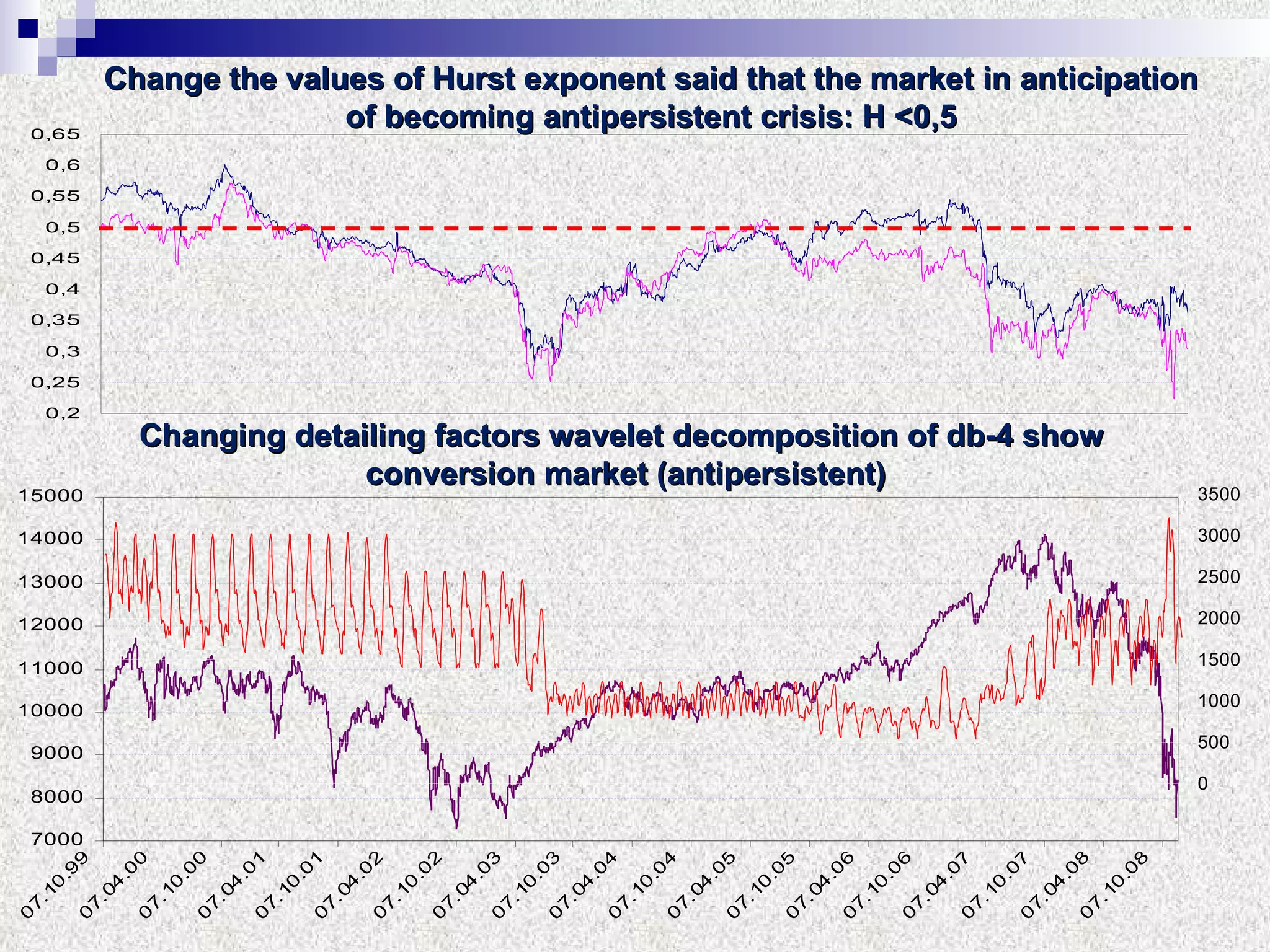
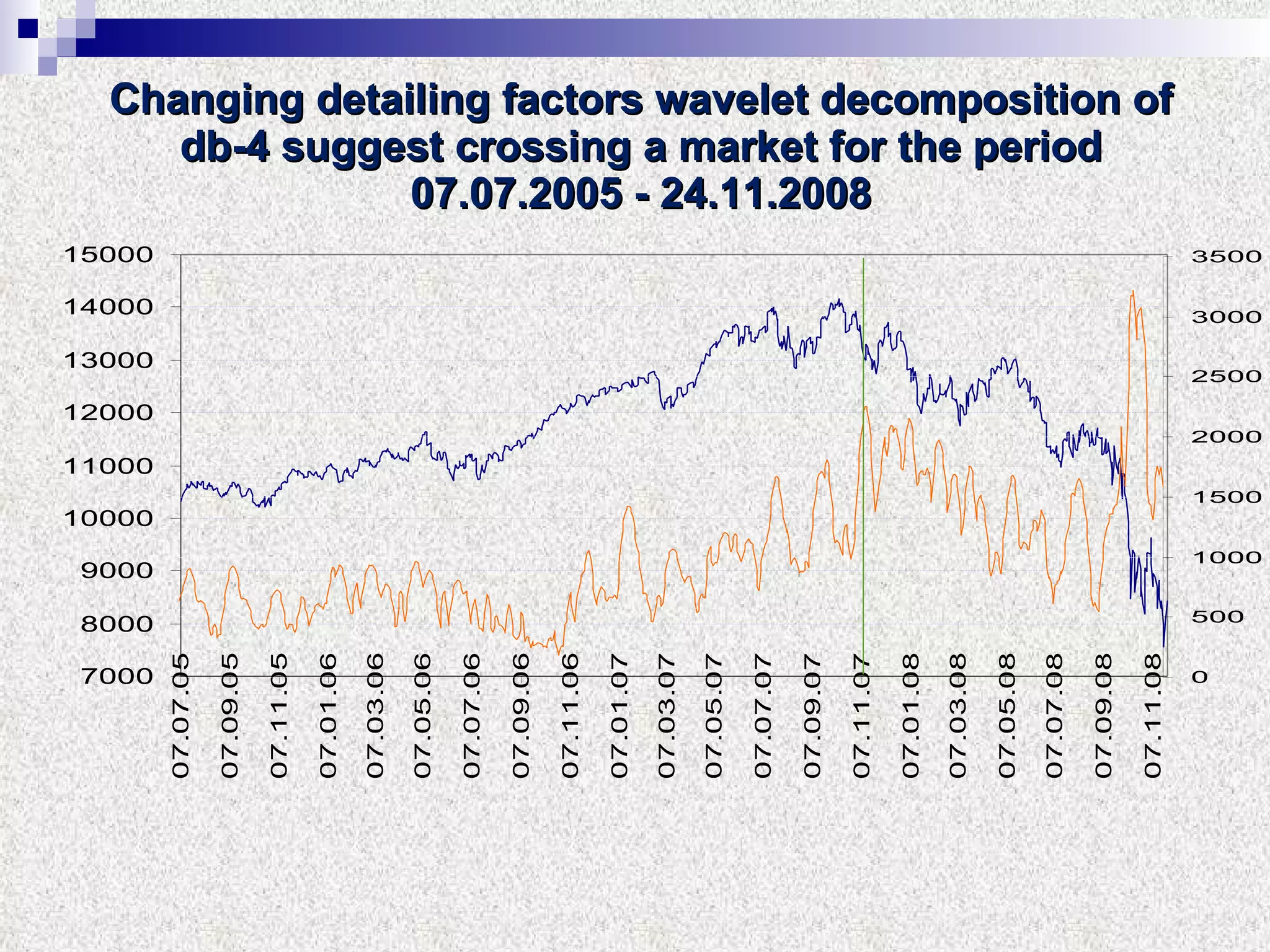
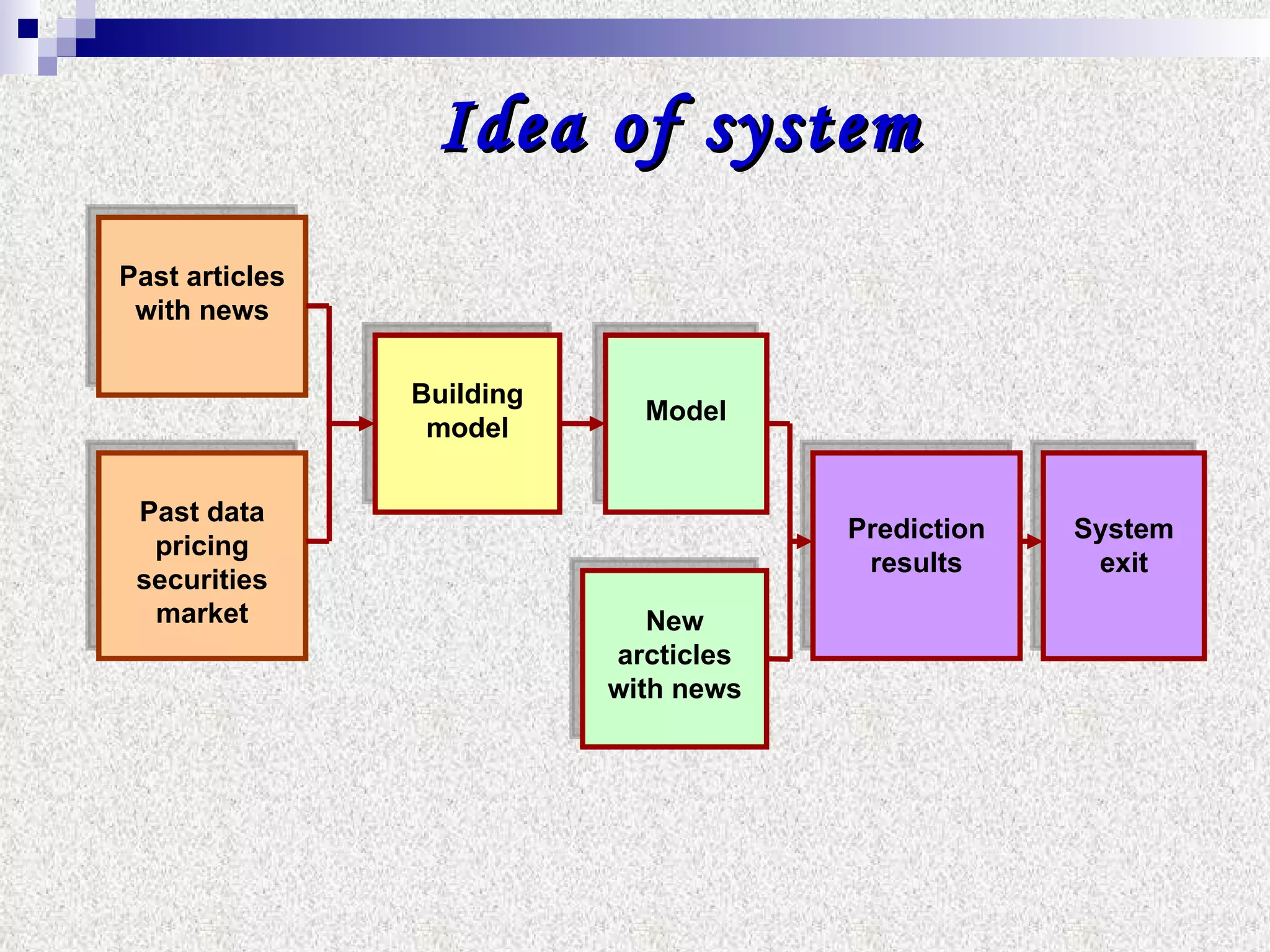
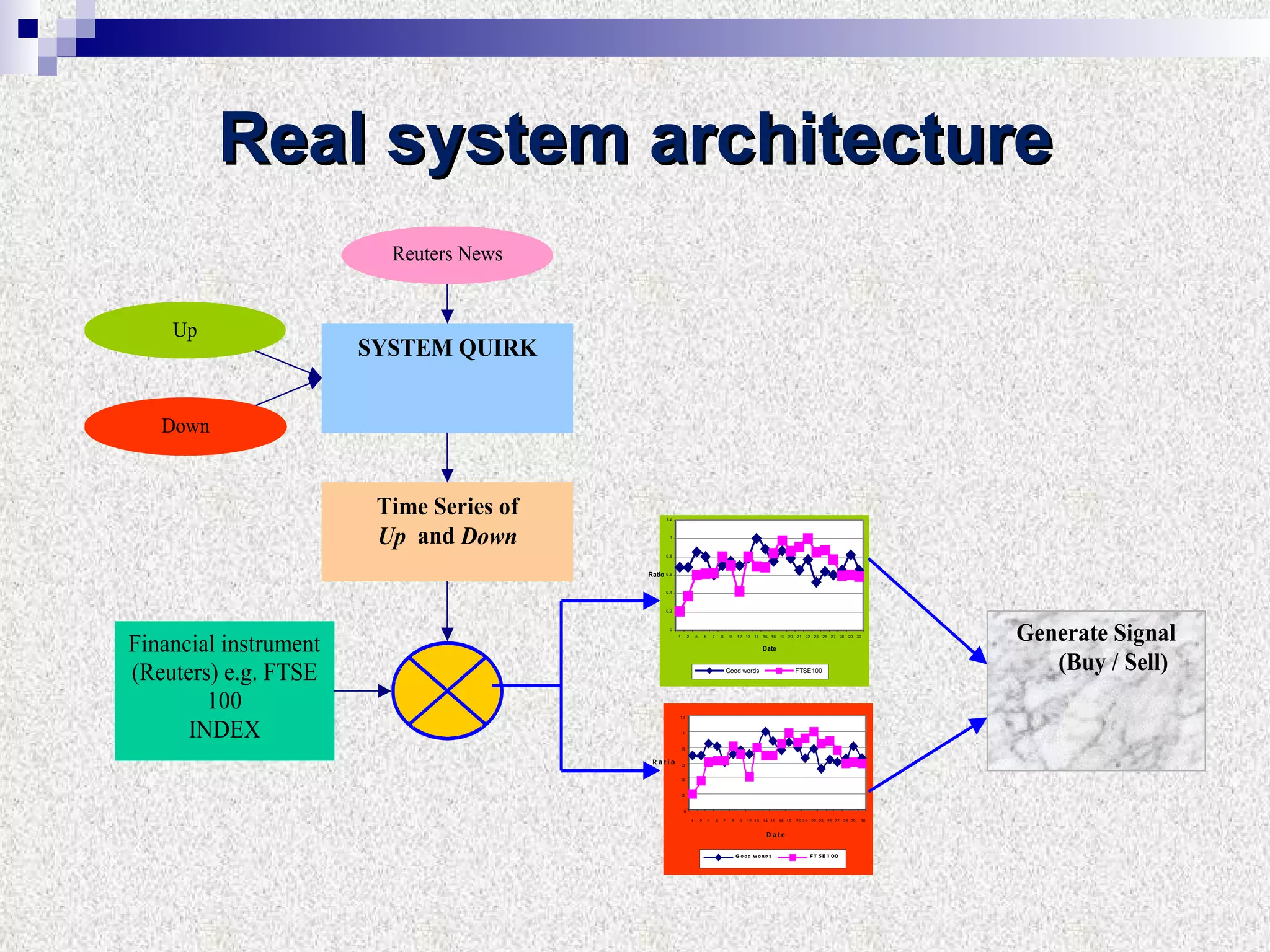
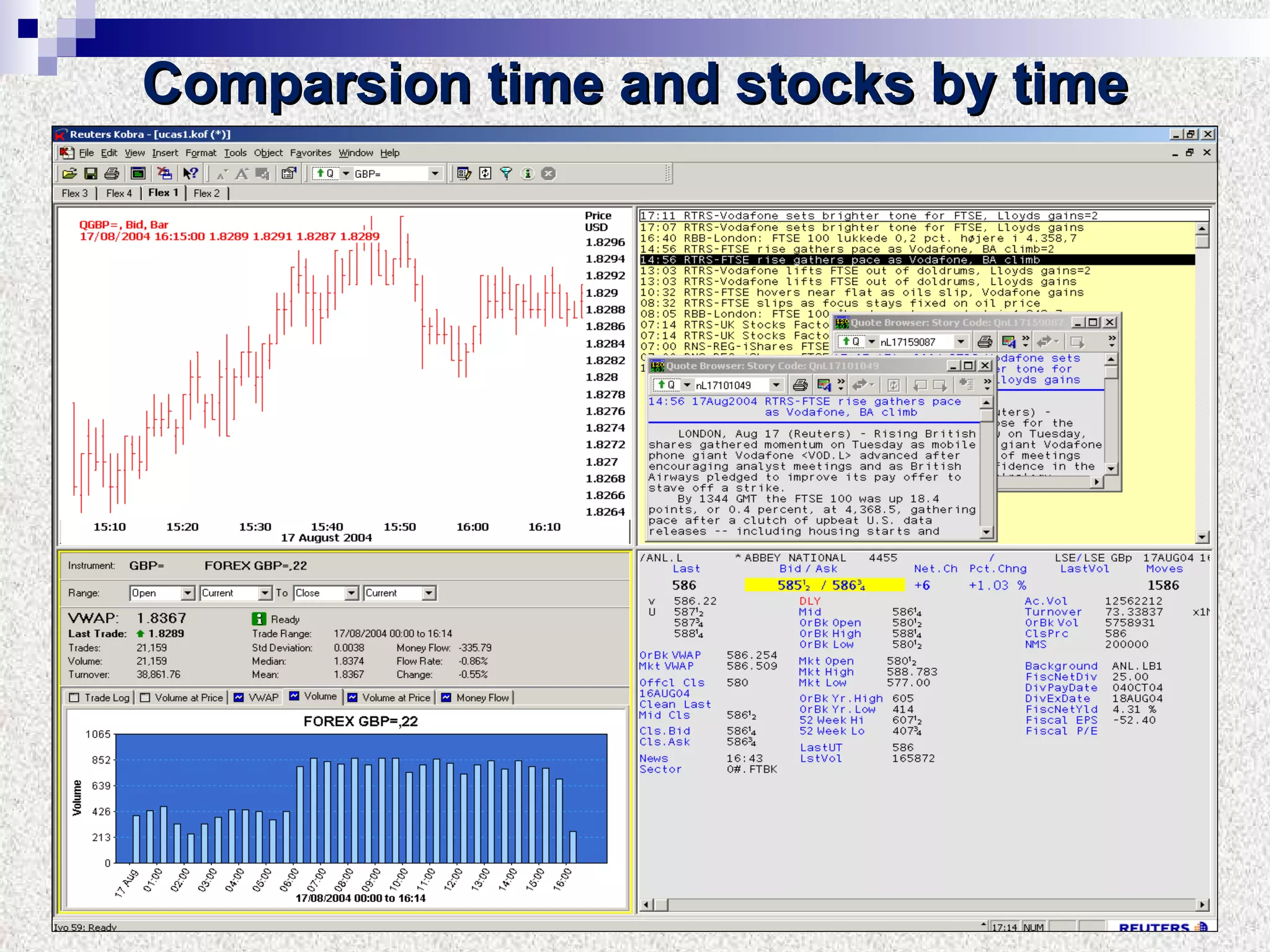
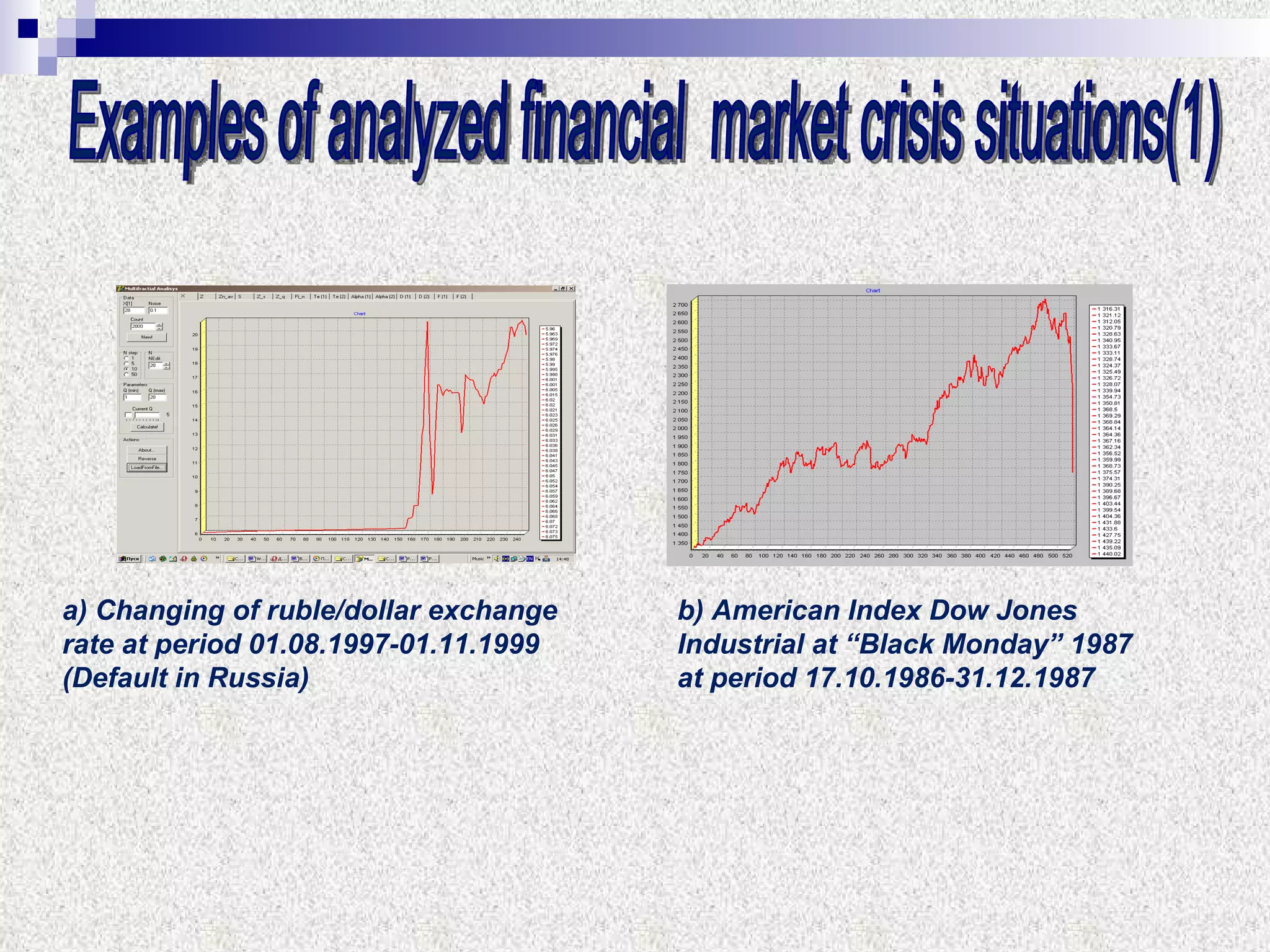
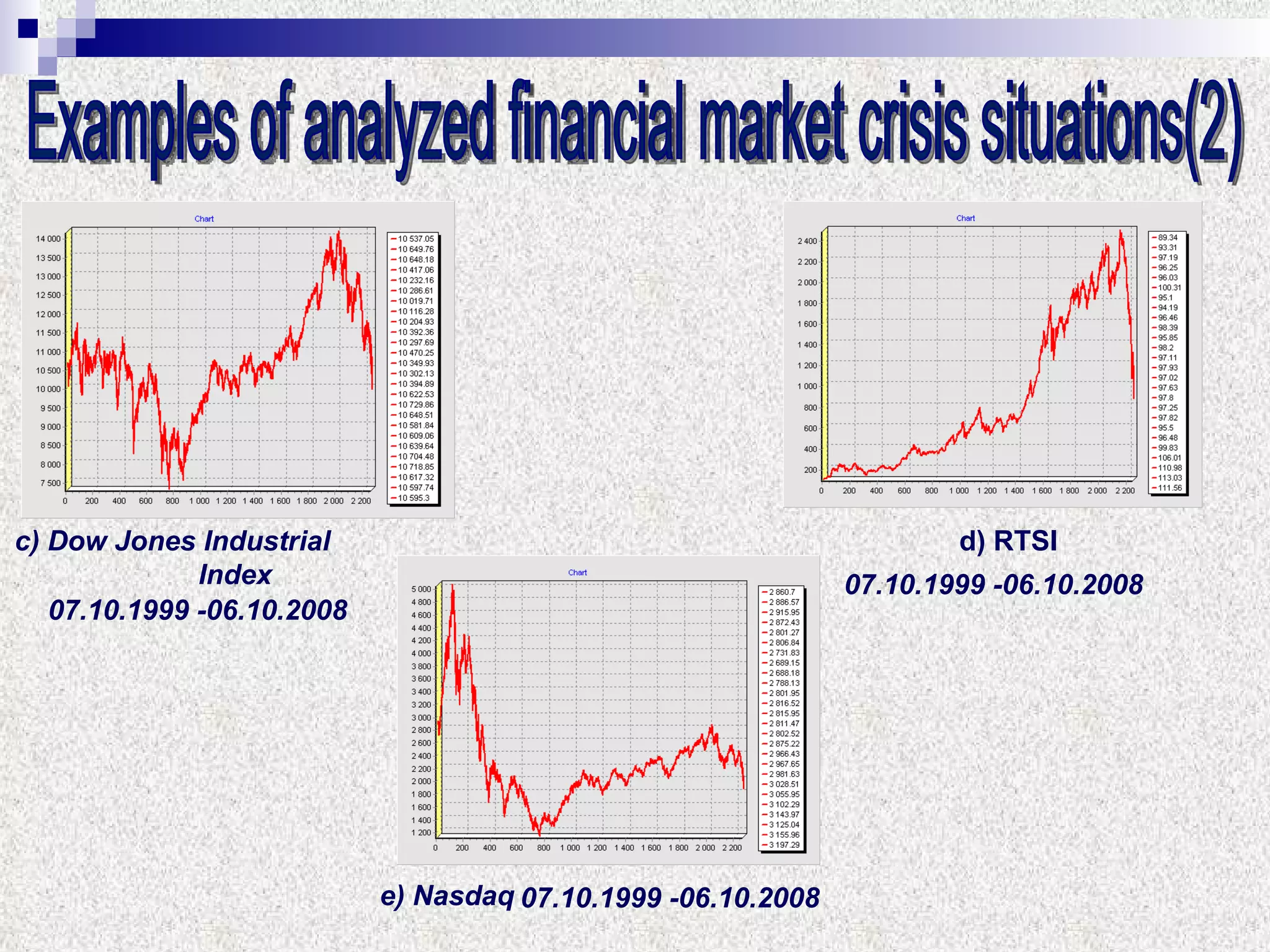
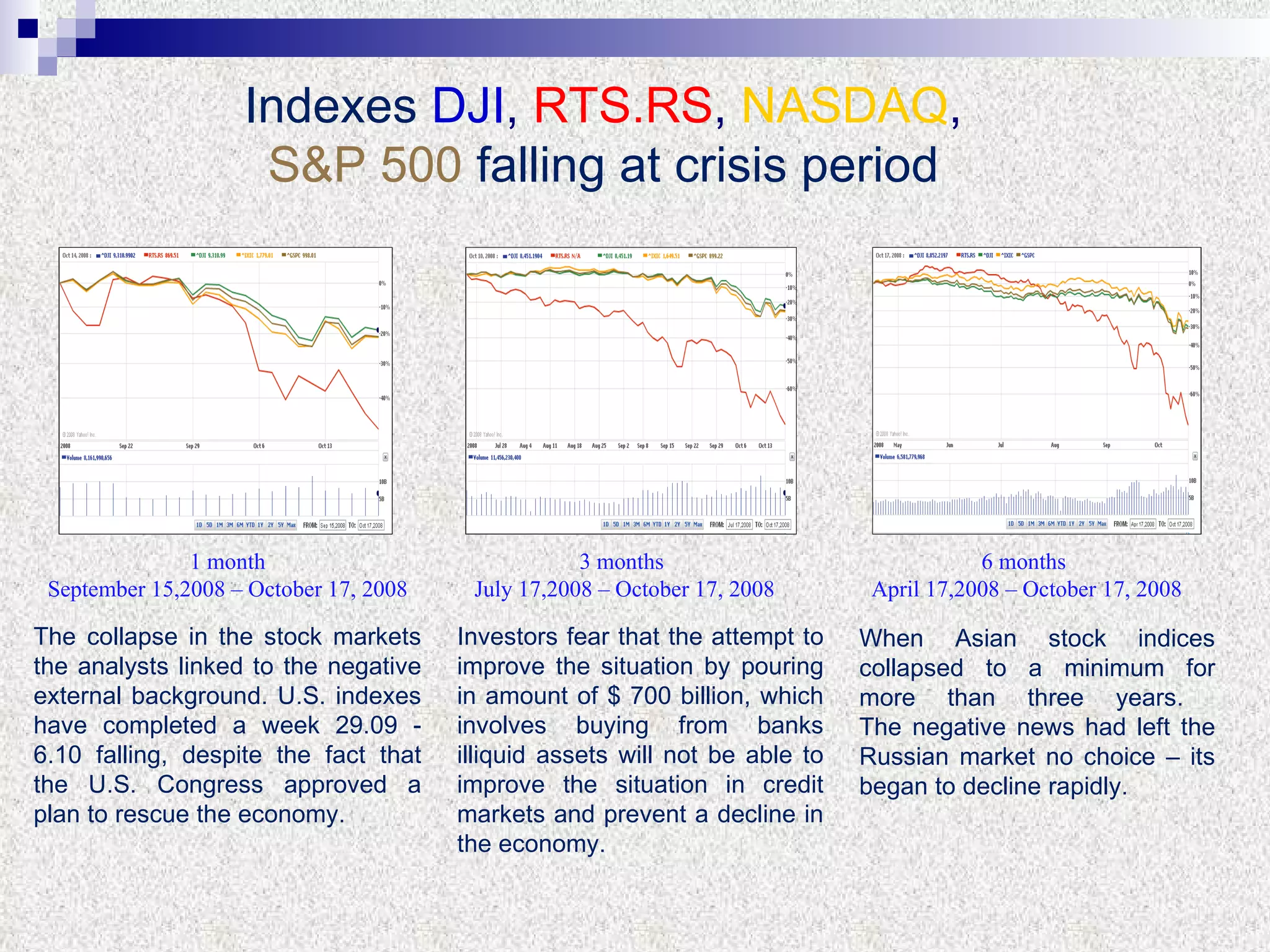
The document discusses using multifractal and wavelet analysis to predict financial market crises. It analyzes various financial market indices during crisis periods from 1987 to 2008. Fractals are described as shapes that appear similar at different scales and have non-integer dimensions. Financial markets exhibit fractal properties with long-term memory and volatility clustering. The researchers use techniques like Hurst exponent analysis, time series partitioning, and calculating partition functions and fractal dimension spectra to analyze indices for signs of an impending crisis. The width of the multifractal spectrum is proposed as an indicator, with wider widths preceding crashes.

1. Financial market crises prediction by multifractal and wavelet analysis. Russian Plekhanov Academy of Economics Romanov V.P., Bachinin Y.G., Moskovoy I.N., Badrina M.V.

2. It is well known, that financial markets are essentially non-linear systems and financial time series are fractals. That’s why prediction of crash situations at finance market is a very difficult task. It doesn’t allow us to use effectively such well-known methods as ARIMA or MACD in view of their sluggishness. Multifractal and wavelets analysis methods are providing more deep insight into the nature of phenomena. Multiagent simulation makes it possible to explicate dynamic properties of the system. The main aim is to find out the predictors or some kind of predicting signals which may warn as about forthcoming crisis The aim of the research

3. a ) Changing of ruble/dollar exchange rate at period 01.08.1997-01.11.1999 ( Default in Russia ) ‏ b ) American Index Dow Jones Industrial at “Black Monday” 1987 at period 17.10.1986-31.12.1987 Examples of analyzed financial market crisis situations(1)

4. с) Dow Jones Industrial Index e) Nasdaq d) RTSI 07.10.1999 - 06.10.2008 07.10.1999 - 06.10.2008 07.10.1999 - 06.10.2008 Examples of analyzed financial market crisis situations(2)

5. Indexes DJI , RTS.RS , NASDAQ , S&P 500 falling at crisis period 1 month S eptember 15,2008 – O ctober 17, 2008 The collapse in the stock markets the analysts linked to the negative external background. U.S. indexes have completed a week 29.09 - 6.10 falling, despite the fact that the U.S. Congress approved a plan to rescue the economy. Investors fear that the attempt to improve the situation by pouring in amount of $ 700 billion, which involves buying from banks illiquid assets will not be able to improve the situation in credit markets and prevent a decline in the economy. 3 months July 1 7 ,2008 – O ctober 17, 2008 When Asian stock indices collapsed to a minimum for more than three years. The negative news had left the Russian market no choice – its began to decline rapidly. 6 months April 1 7 ,2008 – O ctober 17, 2008

6. E fficient M arket H ypothesis ( EMH ) asserts , that financial markets are "informationally efficient", or that prices on traded a ssets, e.g., stocks, bonds, or property, already reflect all known information. The efficient-market hypothesis states that it is impossible to consistently outperform the market by using any information that the market already knows, except through luck. Information or news in the EMH is defined as anything that may affect prices that is unknowable in the present and thus appears randomly in the future. Capital Asset Pricing Model (CAPM) is used to determine a theoretically appropriate required rate of return of an asset, if that asset is to be added to an already well-diversified portfolio, given that asset's non-diversifiable risk. The model takes into account the asset's sensitivity to non-diversifiable risk (also known as systemic risk or market risk), often represented by the quantity beta (β) in the financial industry, as well as the expected return of the market and the expected return of a theoretical risk-free asset. Arbitrage pricing theory ( APT ), in finance, is a general theory of asset pricing, that has become influential in the pricing of stocks. APT holds that the expected return of a financial asset can be modeled as a linear function of various macro-economic factors or theoretical market indices, where sensitivity to changes in each factor is represented by a factor-specific beta coefficient. Financial Market Models

7. Efficient Market Hypothesis versus Fractal Market Hypothesis Efficient market hypothesys ( EMH ) ‏ Assumption of normal distribution of prices increments The weak form EMH from a purely random distribution of prices has been criticized Semi-strong form of EMH, in which all available information is reflected in the prices used by professionals Changing prices in the long run does not show the presence of «memory» Fractral market hypothesys (FMH) Prices shows leptoexcess effect for prices probability distribution ( “fat tails” ) ‏ The prices plot looks similary for the period of time in the day, week, month (fractal pattern) ‏ Reducing the reliability of predictions with the increase of its period Prices shows short-term and long-term correlation and trends (the effect of feedback) ‏ Chaotic activity of the market

8. Fractals – The term fractal was coined in 1975 by Benoît Mandelbrot, from the Latin fractus , meaning "broken" or "fractured". (colloquial) a shape that is recursively constructed or self-similar, that is, a shape that appears similar at all scales of magnification. (mathematics) a geometric object that has a Hausdorff dimension greater than its topological dimension. The second feature that characterizes fractals is the fractional dimension. The word fractal came from fractional values – partial values, which may take the fractal dimension of objects Fractals may cause the application of Iterative Functions System The image, which is the only fixed point of IFS is called attractor Fractal definition

9. Chaos and dynamics of fractal market Market prices tend to level the natural balance within the price range These levels or ranges can be described as «attractors» However, the data within those ranges remain casual

10. Point attractors The simplest form of the attractor. In theory, compatible with the balance of supply and demand in the economy or the market equilibrium. Represent market volatility on balance, or "market noise" Displays Multiple varying the amplitude fluctuation, which are contained within the set limit cycle attractor, called «phase space». Limit cycle attractors Strange or fractal attractors Attractors types

11. Serpinsky Triangle

12. Fractals examples

13. Another fractals examples

14. Fractal attractors and financial markets Stocks and futures - classic examples of securities. Profit from buying and selling comparable with fluctuations in the pendulum Each bearer security or futures contract are located in its own phase space Long-term forecasting is heavily dependent on accurate measurement of initial conditions of the market

15. Fractals on capital market Financial markets describes a nonlinear function of active traders Traditional methods of technical analysis based on linear equations and Euclidean geometry are inadequate Market jumps growth and recession are nonlinear Technical analysis methods are poor indicators of the relationship trend and trading decisions Fractals can describe the phenomena that are not described in Euclidean geometry

16. Stochastic process {x(t)} is called Multifractal, if it has fixed increments and satisfies the condition , when c(q) – predictor , E- operator of mathematical expectation , , – intervals on the real axis . Scaling function taking into account the impact of time on points q . Multifractal

17. Definiting the Fractal Dimension Index Fractal dimension indedx ( FDI ) : NS(1/2 n ) – the number of blocks with a length of hand 1/2 n , which necessary , to cover S – Serpinsky triangle . Где N A (1/ n ) – the number of blocks with length of hand , equal 1/ n , which necessary to cover variety А. Фрактальное Множество А

18. Fractal Dimension Index Defines the persistence or antipersistence of market. Persistent market weakly fluctuated around the market trend antipersistent market shows considerable volatility on the trend antipersistent market is more rugged pricing schedule and more frequently show a change trends

19. Crisis prediction technique Because our goal is the prediction of crises, we are trying to first find out the best indicator, using methodology Multifractal and wavelet analysis. Then we test various types of pre-processing the original time series to find the best indicator.

20. Hurst exponent Depending on the value of Heurst exponent the properties of the process are distinguished as follows: When H = 0.5, there is a process of random walks, which confirms the hypothesis EMH. When H > 0.5, the process has long-term memory and is persistent, that is it has a positive correlation for different time scales. When H < 0.5, time-series is anti-persistent with average switching from time to time.

21. Time series partitioning Time series: { x t } ; t  [0, T ]. Compute : Z ={ z t }, z t = lnx t+1 -lnx t ; t  [0, T ] ; Divide interval [0, T ] into N subintervals , 1 ≤ N ≤ Nmax . Each subinterval contains int ( T/N )= A values Z; For each subinterval K; 1 ≤ K ≤ N current reading number lK; 1 ≤ lK ≤ A; t = ( K -1) А+ lK As soon as we are looking for the best indicator of a coming default, we will use several variants of a preliminary processing.

22. Time series preprocessing 1. The original time series itself: Z ={ z t } ; 2. Preprocessed time series Z 1={ }, K =1,2,… N, where 3. Preprocessed time series where 4. Preprocessed time series Z 3 ={ }

23. Partition functions For each preprocessed time series compute partition function for different N and q values :

24. Scaling functions

25. Fractal dimension spectrum estimation 1. Lipshitz – Hoelder exponent estimation : : when, i = 1, 2, 3, 4. 2. Fractal dimension spectrum estimation by Legendre transform

26. Fractal dimension spectrum width as crash indicator Multifractal may be composed of two or infinite number of monofractals with continuous varying α values. Width of α spectrum may be estimated as difference between maximum and minimum values of α: Δ  =  max -  min , By carrying out Legendre transform we are trying using our program by estimating Δ  to find differences in its values before and after crash. Roughly speaking f(  ) gives us number of time moments, for which degree of polynomial, needed for approximation f(  ) equals  (according to Lipshitz condition).

27. Scaling functions Non-linear scaling function  (q) ( Multifractal process )‏ Changes in currency for the Russian default of 1998

28. Assesment of multifractal spectrum of singularity at period 09.07.96-21.07.98 Assesment of multifractal spectrum of singularity at period 18.11.96-30.11.98 Screenshots assessment of Multifractal spectrum of singularity

29. Dow Jones Industrial Index, pre-crisis situation 19.12.2006-06.10.2008 Scaling functions Non-linear scaling-function  (q) ‏ ( multifractal process ) ‏

30. RTSI index, pre-crisis situation 19.12.2006-06.10.2008 Non-linear scaling-function  (q) ‏ ( multifractal process ) ‏ Scaling functions

31. Scaling functions linear scaling-function  (q) ‏ (monofractal process ) ‏ Assesment of multifractal spectrum of singularity RTSI at period 16.05.2000 - 30.05.2002

32. Screenshots assesment of Multifractal spectrum of singularity Assesment of multifractal spectrum of singularity DJI at period 19.12.2006-08.10.2008 Assesment of multifractal spectrum of singularity RTSI at period 16.12.2003-10.01.2006

33. &quot;Needles&quot; that determine the expansion of Multifractal spectrum on an hourly schedule 5.2008-11.2008

34. Experimental results Schedule assessment of the width of the spectrum of fractal singularity ( Δ (t)= α max - α min ) for different periods of time American Dow Jones at the «Black Monday» 1987 period 17.10.1986-31.12.1987 Schedule assessment of the width of the spectrum of fractal singularity ( Δ (t)= α max - α min ) at the «Black Monday»

35. Graph of Multifractal spectrum singularity width assessment ( Δ (t)= α max - α min ) at russian index RTSI at period 07 .10.19 99 - 07 .1 1 . 2008 interval Qmin Qmax N ∆ 1-512 07.10.1999 –18.10.2001 -2 6 47 0,964 151-662 16.05.2000 - 30.05.2002 -2 6 103 0,495 301-812 15.12.2000 -31.12.2002 -2 6 129 1,62 451-962 25.07.2001 - 11.08.2003 -2 5 31 0,81 601-1112 28.02.2002 - 17.03.2004 -2 6 170 1,77 751-1262 03.10.2002 - 19.10.2004 -2 6 129 2,17 901- 1412 15.05.2003 - 02.06.2005 -2 6 129 1,927 1051-1562 16.12.2003 - 10.01.2006 -2 5 43 0,952 1201-1712 26.07.2004 - 15.08.2006 -2 5 21 0,868 1351-1862 04.03.2005 - 26.03.2007 -2 5 22 0,89 1501-2012 06.10.2005 - 25.10.2007 -2 5 23 0,848 1651-2162 19.05.2006 - 07.06.2008 -2 5 40 0,927 1801-2246 19.12.2006 - 06.10.2008 -2 7 145 2,133 1 765 -22 77 25.09.2006 - 0 7 .1 1 .2008 -2 7 161 2,1 77

36. Experimental results (RTSI) ‏ Graph of Multifractal spectrum singularity width assessment ( Δ (t)= α max - α min ) at russian index RTSI at period 07 .10.19 99 - 07 .1 1 . 2008 Over 4 years outstanding mortgage loans in Russia rose more than 16 times - from 3.6 billion rubles. in 2002 to 58.0 billion rubles. in 2005. In quantitative terms - from 9,000 loans in 2002 to 78,603 in 2005. Why mortgage evolving so rapidly? Many factors. This increase in real incomes and the decline of distrust towards mortgage, as from potential buyers, and from the sellers, and a general reduction in the average interest rate for mortgage loans from 14 to 11% per annum, and the advent of Moscow banks in the regions, and intensifying in the market of small and medium-sized banks. Pre-crisis situation: July 2008 - the beginning of september 2008

37. Graph of Multifractal spectrum singularity width assessment ( Δ (t)= α max - α min ) at Russian index RTSI at period 07 .10.19 99 - 09 .1 2 . 2008

38. Graph of Multifractal spectrum singularity width assessment ( Δ (t)= α max - α min ) at american index Dow Jones Industrial at period 07 .10.19 99 - 07 .1 1 . 2008 interval Qmin Qmax N ∆ 1-512 07.10.1999 –18.10.2001 -2 5 164 1,84 151-662 16.05.2000 - 30.05.2002 -2 4 5 0,717 301-812 15.12.2000 -31.12.2002 -2 5 134 1,77 451-962 25.07.2001 - 11.08.2003 -2 5 65 1,01 601-1112 28.02.2002 - 17.03.2004 -2 5 74 1,108 751-1262 03.10.2002 - 19.10.2004 -2 4 11 0,791 901- 1412 15.05.2003 - 02.06.2005 -2 4 38 0,803 1051-1562 16.12.2003 - 10.01.2006 -2 4 50 0,815 1201-1712 26.07.2004 - 15.08.2006 -2 4 53 0,884 1351-1862 04.03.2005 - 26.03.2007 -2 4 57 0,973 1501-2012 06.10.2005 - 25.10.2007 -2 4 29 0,864 1651-2162 19.05.2006 - 07.06.2008 -2 4 11 0,836 1801-22 63 19.12.2006 - 06.10.2008 -2 5 151 2,324 1 765 -22 84 25.09. 2006 - 0 7 .1 1 .2008 -2 5 1 74 1,984

39. There was a sharp drop in the index and 9 october 2002 DJIA reached an interim minimum with a value of 7286,27. Dow Jones Industrial index of 15 september 2008, fell to 4.42 per cent to 10,917 points - is the largest of its fall in a single day since 9 october 2002, reported France Presse. World stock markets experienced a sharp decline in major indexes in connection with the bankruptcy Investbank Lehman Brothers. Graph of Multifractal spectrum singularity width assessment ( Δ (t)= α max - α min ) at american index Dow Jones Industrial at period 07 .10.19 99 - 07 .1 1 . 2008 Experimental results(DJI) 3 May, 1999, the index reached a value of 11014.70. Its maximum - mark 11722.98 - Dow-Jones index reached at 14 January 2000. Pre-crisis situation: July 2008 - the beginning of september 2008

40. Graph of Multifractal spectrum singularity width assessment ( Δ (t)= α max - α min ) at american index Dow Jones Industrial at period 07 .10.19 99 - 09 .1 2 . 2008

41. Graph of Multifractal spectrum singularity width assessment ( Δ (t)= α max - α min ) at american index NASDAQ Composite at period 07 .10.19 99 - 07 .1 1 . 2008 interval Qmin Qmax N ∆ 1-512 07.10.1999 –18.10.2001 -2 6 47 0,91 151-662 16.05.2000 - 30.05.2002 -2 6 57 0,935 301-812 15.12.2000 -31.12.2002 -2 6 86 1,092 451-962 25.07.2001 - 11.08.2003 -2 5 25 0,74 601-1112 28.02.2002 - 17.03.2004 -2 5 31 0,821 751-1262 03.10.2002 - 19.10.2004 -2 5 129 1,385 901- 1412 15.05.2003 - 02.06.2005 -2 4 9 0,726 1051-1562 16.12.2003 - 10.01.2006 -2 4 13 0,765 1201-1712 26.07.2004 - 15.08.2006 -2 4 19 0,78 1351-1862 04.03.2005 - 26.03.2007 -2 4 19 0,792 1501-2012 06.10.2005 - 25.10.2007 -2 4 15 0,778 1651-2162 19.05.2006 - 07.06.2008 -2 4 5 0,772 1801-22 63 19.12.2006 - 06.10.2008 -2 5 77 1,185 1 765 -22 84 25 . 09 .2006 - 0 7 .1 1 .2008 -2 6 20 7 1, 067

42. Experimental results(NASDAQ) Graph of Multifractal spectrum singularity width assessment ( Δ (t)= α max - α min ) at american index NASDAQ Composite at period 07 .10.19 99 - 07 .1 1 . 2008 In August 2002 the first NASDAQ closes its branch in Japan, as well as closing branches in Europe, and now it was turn European office, where for two years, the number of companies whose shares are traded on the exchange fell from 60 to 38. After that happened result in a vast dropIn 2000, he reached even five thousandth mark, but after the general collapse of the market of computer and information technology is now in an area of up to two thousand points. The index of technology companies NASDAQ Composite reached its peak in March 2000. Pre-crisis situation: July 2008 - the beginning of september 2008

43. Graph of Multifractal spectrum singularity width assessment ( Δ (t)= α max - α min ) at american index NASDAQ Composite at period 07 .10.19 99 - 09 .1 2 . 2008

44. Default’s 1998 indicator. a) ‏ b) ‏ Part Multifractal spectrum of data related to graph b) ‏ The red line shows that the width multifraktalnogo spectrum begins to grow at the same time as changing the exchange rate, but more clearly. Данные  min  max  11.08.98 2,837 3,337 0,5 12.08.98 2,837 3,335 0,498 13.08.98 2,838 3,325 0,487 14.08.98 2,839 3,344 0,505 17.08.98 1,8 3,36 1,56 18.08.98 1,97 3,3 1,33 19.08.98 1,355 3,26 1,905 20.08.98 1,499 3,264 1,765 21.08.98 1,499 3,4 1,901 24.08.98 1,5 3,249 1,749

45. Wavelet-analysis где   ,  (t) – where   ,  (t) – function with zero mean centered around zero with time scale  and time horizon  . Family of wavelet vectors is created from mother function by displacement and scaling

46. Time series f(t) representation as linear combination of wavelet functions where j o – a constant, representing the highest level of resolution for which the most acute details are extracted .

47. WA crisis detection experiment - 1 In our study we used D au be c hi es wavelet functions decomposition (db-4 и db-12). The goal was the detection of the signal, which could predict the sudden changes. Data on exchange rates (USD) to the ruble were taken from the site www.rts.ru for the period 1.09.1995 - 12.02.1999 The total number of numbered in the order several times in the interim for the period 1.09.1995 - 12.02.1999 was 862 value.

48. Graph of changing RTS indexes at period 1.09.1995 – 12.02.1999

49. The division time series on the ranges To achieve the goal of this time series was divided into 7 overlapping intervals located unevenly, so that the interval 4 (242-753) immediately preceding the time of default and subsequent intervals captured the moment of default. Each interval consisted of 512 values: 1-512, 101-612, 201-712, 242-753, 251-762, 301-812, 351-862.

50. Predicting the crisis with the help of wavelet analysis The schedule change ratios of difference from the average value of currencies this intervala to the value of the previous intervala for the period 19.09.1997-12.02.1999 (dates are taken on the right border, ie 512 value). The schedule changes difference ratios of maximum ratios of decomposition of Dobeshi-12 for the period 19.09.1997-12.02.1999 (dates are taken on the right border, ie 512 value) ‏ # Interval Maximum for all levels Difference maximum ratios 1 1-512 0,068796 - 2 101-612 0,140859 0,072062 3 201-712 0,150173 0,009314 4 242-753 11,234599 11,084426 5 251-762 11,850877 0,616278 6 301-812 7,944381 -3,906496 7 351-862 9,802439 1,858058 # interval Average value Difference averages 1 1-512 5,249121 - 2 101-612 5,518002 0,268881 3 201-712 5,759273 0,241271 4 242-753 5,926961 0,167688 5 251-762 6,077492 0,150531 6 301-812 7,124922 1,047431 7 351-862 8,672407 1,547484

51. The schedule changes difference maximum coefficients of expansion in the Dobeshi-12 (17.10.1986-31.12.1987). The difference coefficients of D au be c hi es -12 № interval Maximum for all levels Difference maximum ratios 1 1-128 13083,070 -------------- 2 64-192 223,834 -12859,235 3 96-224 262,039 38,204 4 106-234 258,122 -3,916 5 111-239 262,371 3,917 6 114-242 14785,540 14523,169 7 124-252 789,933 -13995,607 8 126-254 1298,050 508,117 9 177-305 475,376 -822,673

52. «Black Monday» Detector At the previous slide we can see the positive peak earlier 01.10.87 and negative peak before 15.10.87. This is more than 4 days before the «Black Monday». Sharp line connects the two peaks. Obviously, this information can serve as a detector impending crisis.

53. 42 days prior to the default Of the figure shows that the start of trading, the corresponding spike in the dollar may be adopted point 742 (21.08.1998), a peak corresponds to 754 points (07.09.1998). As we can see from the previous slide in the event of data processing by the Russian default by default, if we use the average of the indicator is the intervals difference, then we can find that the sharp increase occurring 18.09.1998, ie delayed by at least 11 days. At the same time schedule for the coefficients of wavelet functions shows us that the beginning of dramatic changes difference wavelet coefficients of expansions is a point 712 (10.07.1998). We can, apparently, to predict the onset of default at least 42 days (10.07.1998 - 21.08.1998). At the same time increase the maximum value (Fig. 4) of this indicator in the starting time was 74.5 times (initial value = 0.15; following value = 11.23) ‏

54. WA crisis detection experiment - 2 In our experiment, number 2, we used D au be c hi es wavelet functions decomposition (db- 4 ). The goal was the detecting the signal, which could predict the sudden changes in the index DJI (Dow Jones Index - Dow Jones). Data on DJI were taken from the site http://finance.yahoo.com for the period 7.10.1999 - 24 .1 1 .2008 The total number of numbered in the order several times in the interim for the period 7.10.1999 - 24 . 11 .2008 at 22 99 values.

55. Graph DJI change 7.10.1999- 8 .1 1 .2008

56. Change the values of Hurst exponent said that the market in anticipation of becoming antipersistent crisis: H <0,5 Changing detailing factors wavelet decomposition of db-4 show conversion market (antipersistent)

57. Changing detailing factors wavelet decomposition of db-4 suggest crossing a market for the period 07.07.2005 - 24.11.2008

58. Fundamental analysis Fundamental analysis is based on an assessment of market conditions in general and assessing the future development of a single issuer. Fundamental analysis is a fairly laborious and a special funding agencies. Fundamental analysis depends on the news of factors. By random and unexpected news include political and natural, as well as war. How to conduct a fundamental analysis can be divided into four separate units, correlating with each other.

59. Fundamental analysis technology The first unit - is a macroeconomic analysis of the economy as a whole. The second unit - is an industrial analysis of a particular industry. A third unit - a financial analysis of a particular enterprise. A fourth unit - analyzing the qualities of investment securities issuer. Fundamental analysis technology includes an analysis of news published in the media, and comparing them with the securities markets.

60. Analysis Method Keyword extraction, characterizing the market: boost or cut, the increase / decrease. Automatic analysis using the terminology the ontology. Processing time series (filtering, providing trends, the seasonal components). Using neural networks to classify the flow of news and processing time series.

61. Examine what news articles relevant to the company, Yahoo uses profiling to establish consistency between articles and companies. For each trend formed a temporary window to explore how art relates to the trend. It is believed that there is a match, if the article appeared a few hours before the trend. News analysis target

62. The intensity of the flow of news data The joint processing of digital and text data Digital data Time series The movement of financial instruments (price / volume) ‏ Flow intensity: 5Mb/day, on the tool Text data Text flows Various types: News, financial reports, company brochures, government documents Flow intensity: 20 Mb / day

63. Idea of system Past articles with news Past data pricing securities market Building model Model New arcticles with news Prediction results System exit

64. Real system architecture

65. Comparsion time and stocks by time

66. Text analysis should apply: Recognition of the named entity. The discovery of those (people), organizations, currencies. Extracting key information related to organizations, persons, facts, evidence from documents. The establishment of relations between the patterns. Creating a template to scripting events, organizations, regions. The formation of coherence - to collect information on sovstrechaemosti expressions. The result of the system is the text as a set of the following components: <AGENT> <CONCERN> <GOAL> <AGENT> <CONCERN, THE IMPORTANCE> <GOAL, the value> Between formed in such a description of news and current prices of assets in the securities market established statistical connection to predict price changes depending on the nature of news.

67. Fundamental analysis ontology

68. News, alter securities course

69. Automatic 3-side integration Competetive researches , discovered automatically Concentrated content, organised with semantic categories Relevant content, not expressed evidently (semantic associations) Automatic content integration from sources and other providers Fundamental analysis results with ontology using

70. Price graphs and charts Pricing models calls figures or creatings, which appers on price graphs These figures, or education (chart pattern), divided into some groups and can be used to predict the market dynamics