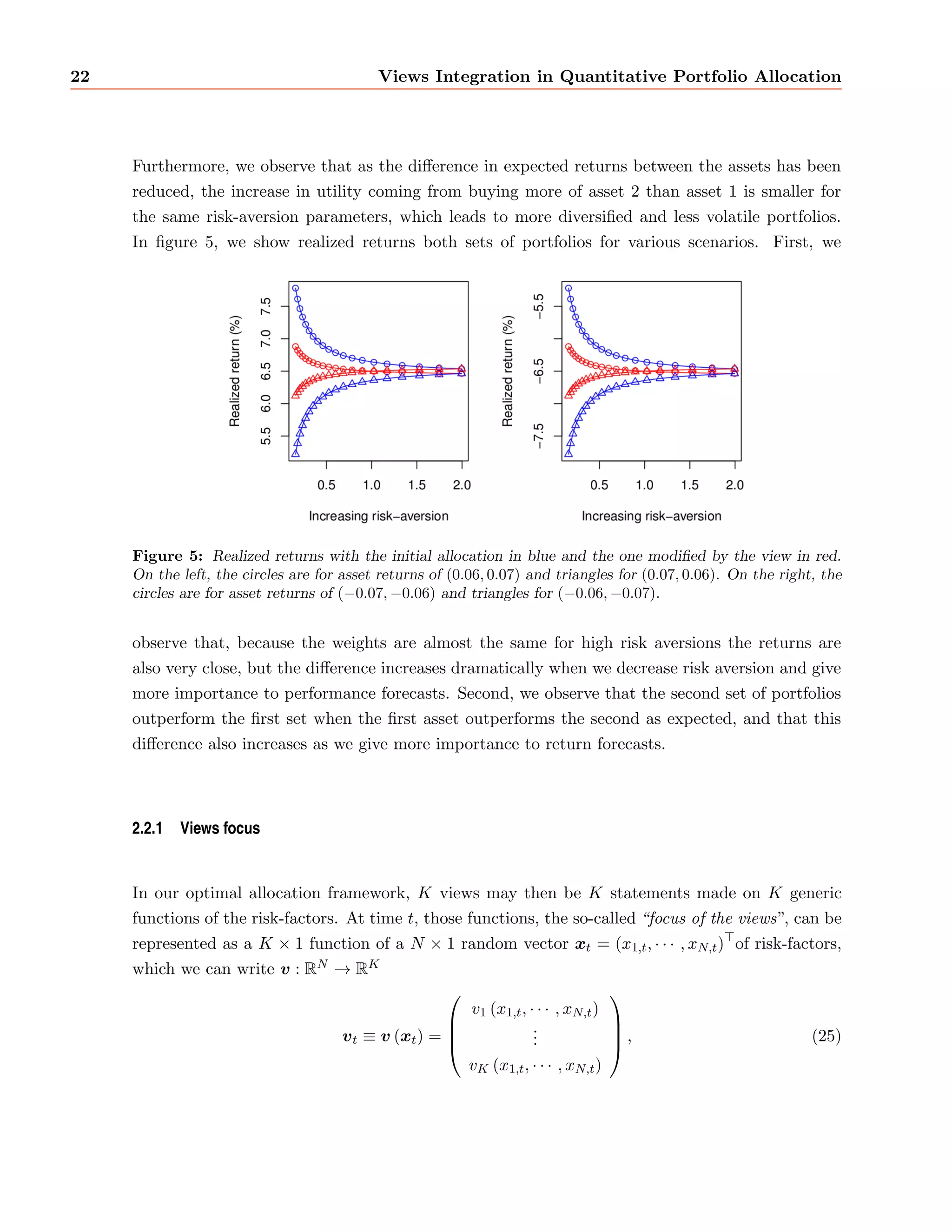
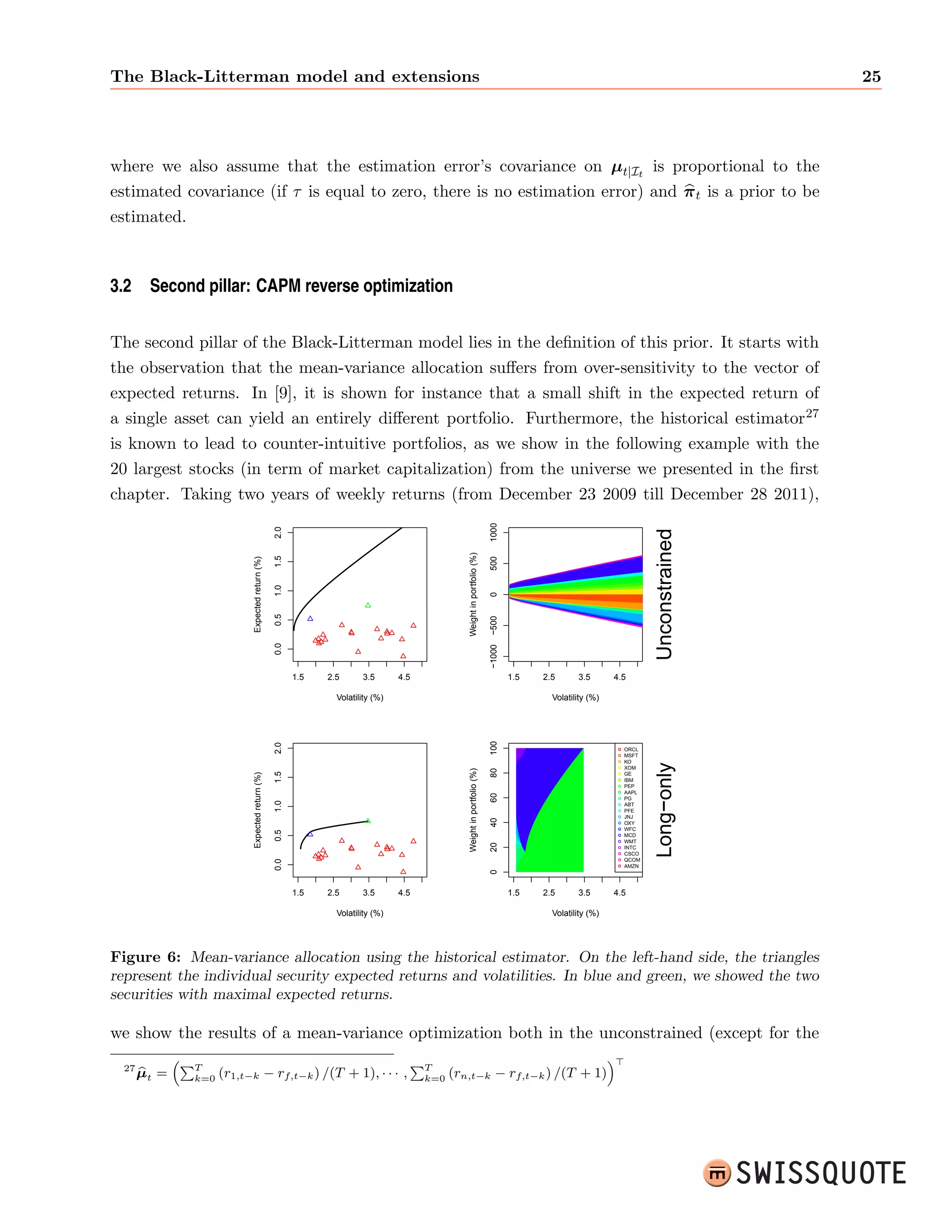
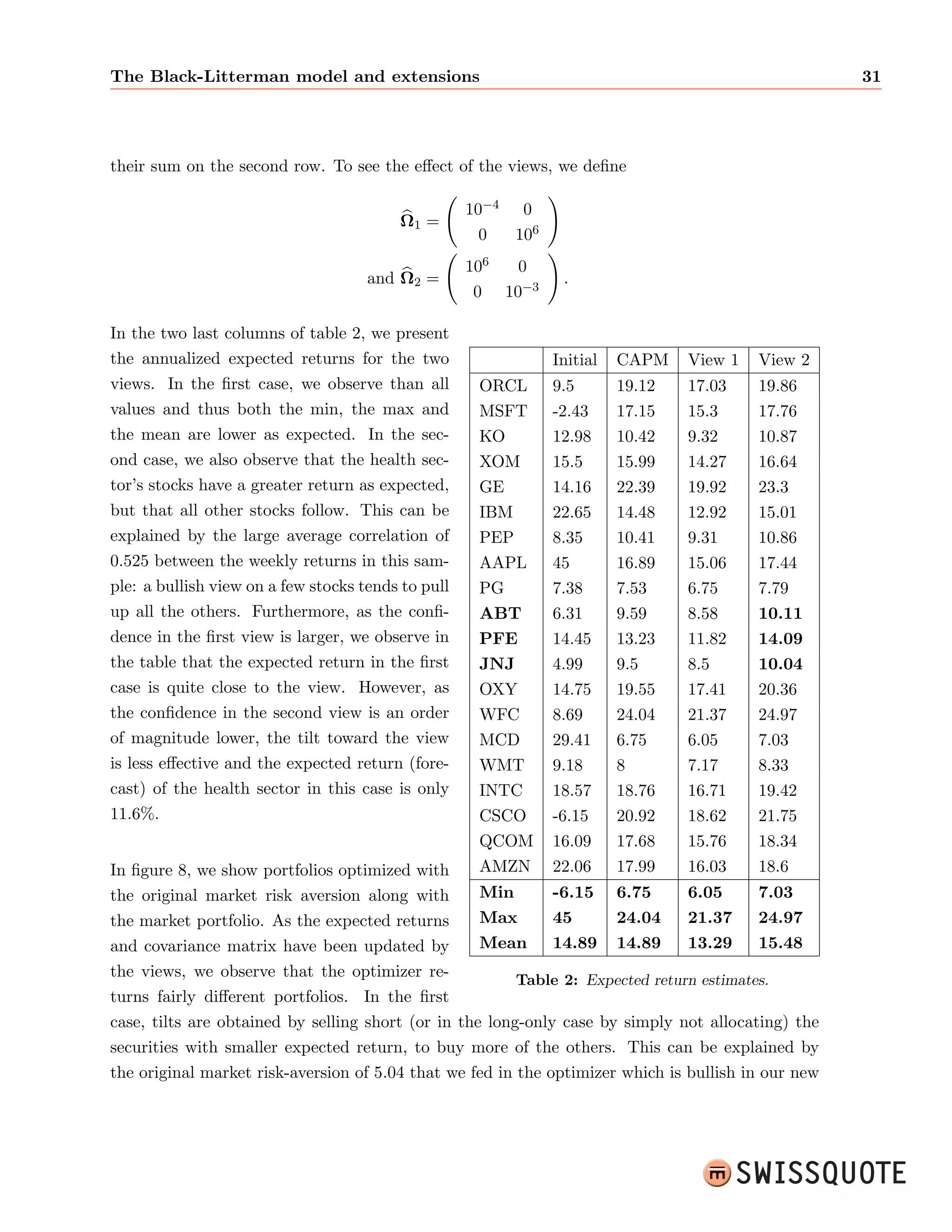
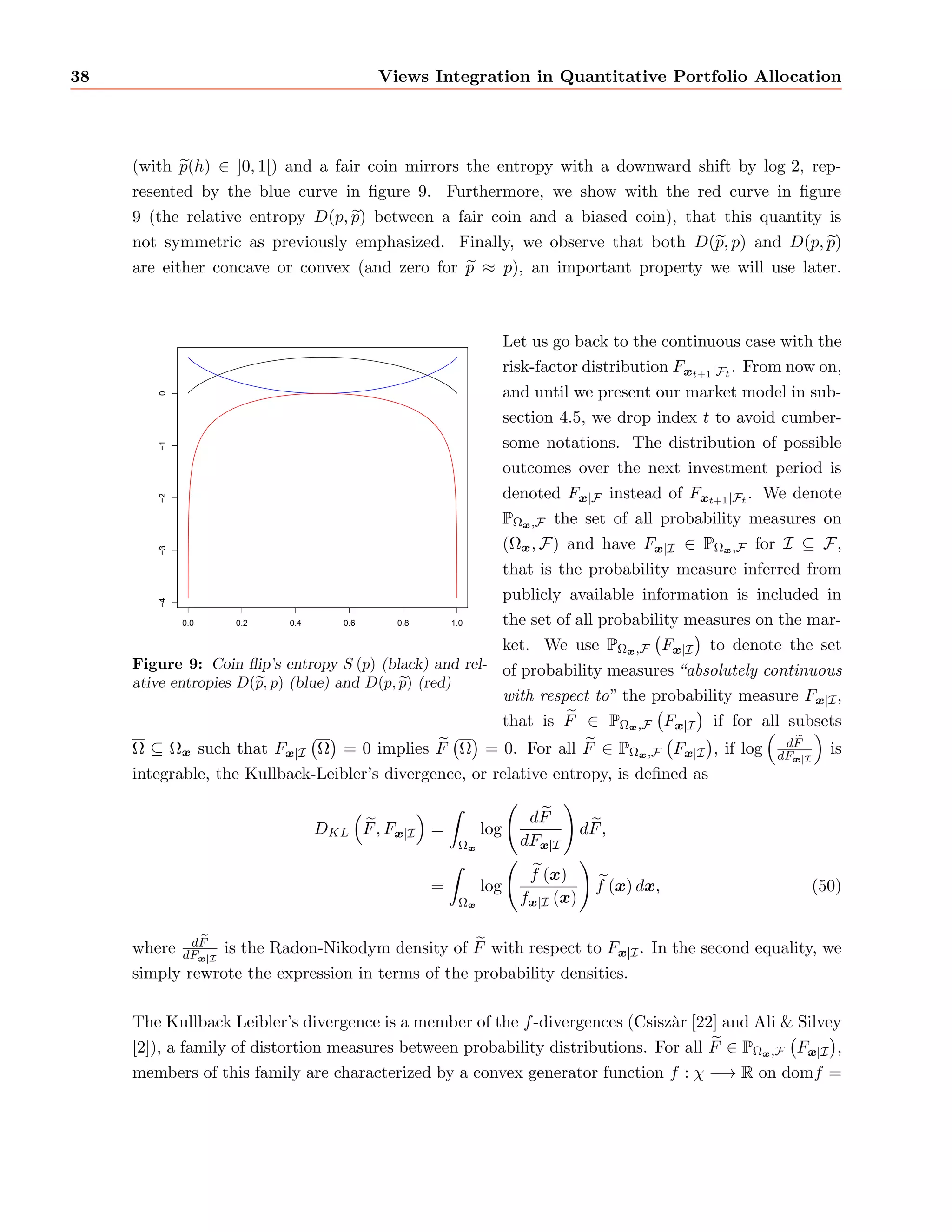
This document summarizes a master's thesis on integrating market views into quantitative portfolio allocation. It introduces the concepts of optimal asset allocation, mean-variance optimization, and dimension reduction using linear factor models. It then discusses incorporating investor views through information sets and the efficient market hypothesis. The Black-Litterman model uses a Gaussian market assumption, CAPM reverse optimization, and Bayesian updating to integrate views. An alternative approach uses f-divergences to measure distortions between probability distributions and translate views into information gain. The thesis concludes by proposing directions for future research.

1. Views Integration in a Quantitative Portfolio Allocation
Master Thesis of Thibault Vatter1;2
Supervized by David Morton de Lachapelle2 and Paolo De Los Rios1
Abstract Modi

2. cations of statistical forecasts by investors having a particular percep-tion
of future market conditions prove to be of utmost importance in practice. In this
thesis, we investigate the eects of market views and review dierent possibilities to
incorporate them in a quantitative scheme. In the

3. rst section, we start by recalling
the optimal allocation problem and set the notations. In the second section, we re-view
the concepts of information sets and ecient market hypothesis and formalize the
incorporation of views in a quantitative framework. In the third section, we present
the path-breaking approach of Black and Litterman, capitalizing on Gaussian markets,
the CAPM and Bayes rule. In the fourth section, we oer new insights into Meucci's
approach, translating views into information gain using f-divergences as a measure of
distortion between distributions. In the

4. fth section, we conclude on the project and
give directions of interest for the future.
1LBS - Institute of Theoretical Physics, EPFL, thibault.vatter@epfl.ch
2QAM Department, Swissquote Bank SA, thibault.vatter@swissquote.ch

5. 2 Views Integration in Quantitative Portfolio Allocation
Contents
1 Introduction 4
1.1 Quantitative portfolio allocation . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
1.2 The mean-variance allocation scheme . . . . . . . . . . . . . . . . . . . . . . . . . 6
1.3 A general formalism . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
1.4 Dimension reduction and linear factor models . . . . . . . . . . . . . . . . . . . . 12
1.5 The Fama{French three-factor model and market benchmarks . . . . . . . . . . . 14
2 Quantitative integration of market views 17
2.1 Information sets, ecient market hypothesis and market views . . . . . . . . . . 17
2.2 Problem formalization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
2.2.1 Views focus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.2.2 Views integration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
3 The Black-Litterman model and extensions 23
3.1 First pillar: a Gaussian market . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
3.2 Second pillar: CAPM reverse optimization . . . . . . . . . . . . . . . . . . . . . . 25
3.3 Third pillar: Bayesian views integration . . . . . . . . . . . . . . . . . . . . . . . 28
3.4 The Augmented Black-Litterman model . . . . . . . . . . . . . . . . . . . . . . . 32

6. CONTENTS 3
4 The scenario-based approach 36
4.1 Learning from disorder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
4.2 Analytical example . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
4.3 Fully
exible probabilities . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
4.4 Relative entropy minimization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44
4.5 Copulas and
exible market models . . . . . . . . . . . . . . . . . . . . . . . . . . 46
4.5.1 Time-varying dynamics . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
4.5.2 Some useful copulas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
4.5.3 Dependence structure estimation . . . . . . . . . . . . . . . . . . . . . . . 53
4.5.4 Closing the model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
4.6 Numerical example : portfolio stress testing . . . . . . . . . . . . . . . . . . . . . 57
4.6.1 Measures of market risk . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
4.6.2 Stress testing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
4.7 Numerical example: mean-variance, market equilibrium and relative entropy . . . 60
5 Conclusion 61
6 Acknowledgments 63
A The Fama and French factors 68
B Jensen-Shannon's divergence minimization 69
C Mean-CV aR optimization 70

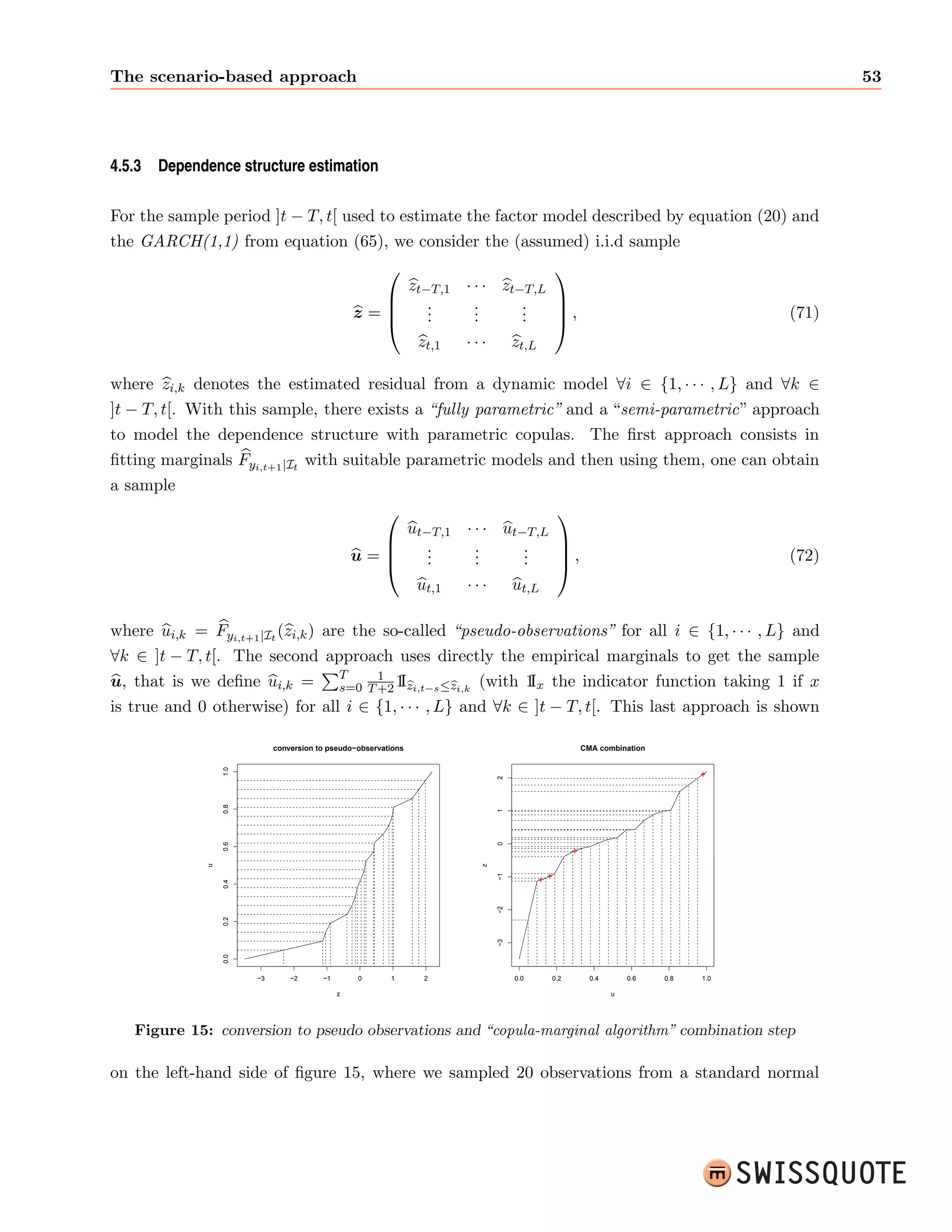
7. 4 Views Integration in Quantitative Portfolio Allocation
1 Introduction
To use the [expected returns-variance] rule in the selection of securities we must have proce-
dures for

8. nding reasonable i and ij . These procedures, I believe, should combine statistical
techniques and the judgment of practical men.
Harry Markowitz, 1952
Since its begining with Markowitz in 1952, modern portfolio theory mixes art and science: judg-
ment of practical men and powerful statistical techniques. The two approaches, although
complementary, are sometimes dicult to conciliate. While practitioners frequently discard
quantitative strategies as obscures mathematical complications,

9. nancial engineers forget that
portfolio management is often about common sense. We attempt to reconcile both in a sound
theoretical and practical framework. In this scope, we review methods allowing the alteration
of statistical forecasts by an investor having a particular perception of future market conditions;
these modi

10. ed forecasts contain the investor's views in suitable form for a quantitative portfolio
allocation.
The idea is to set in a single frame current approaches and related concepts to formalize this
problem and bring sound theoretical and practical answers. We choose to adopt a general for-malism
without elaborating much on the underlying technical concepts. In order to keep the
reader a
oat, we try to give as many heuristic justi

11. cations, intuitions and numerical example
as possible rather than hard proofs. We start with the basics and progress towards increasingly
complex methods while keeping practical applicability in mind, at the cost of simplifying some-times
drastically real-world situations and behaviors. We assume only that the reader is familiar
with the basics of probability and statistics (from an introductory university level course), and
we try to make the

12. nance notions as self-contained as possible.
This thesis is organized as follows. In the

13. rst section, we expose the problem of optimal asset
allocation along with useful notations and practical examples. We also introduce the issue of
dimension reduction and linear models, as exogenous factors are often the focus of practitioners
views. In the second section, we de

14. ne what kind of information is relevant for portfolio opti-mization
in the context of the ecient market hypothesis of Fama. Then, we formalize the
problem of incorporating this information into an actual allocation. In the third section, we start
as often in

15. nance with the Gaussian description of markets. Using the CAPM1 equilibrium and
1Introduced by William Sharpe and John Lintner, the Capital Asset Pricing Model describes the relationship
between a security risk and its associated premium.

16. Introduction 5
Bayes rule, the Black-Litterman model brings the

17. rst answer to the problem. In the fourth
section, we leave Gaussian markets for more advanced statistical modelling and use the concept
of distortion between distributions to translate market views into information gain. To generate
the required Monte-Carlo simulations and test this technique in various situations, we present
an advanced and
exible market model. Finally, we conclude in the

18. fth section and propose
directions for further research.
1.1 Quantitative portfolio allocation
Let us de

19. ne si;t, the price at time t of security i (typically i can be a stock representing partial
ownership of a

20. rm). Holding this security from time t1 to time t yields the one-period simple
return
ri;t =
si;t si;t1
si;t1
: (1)
Working with returns instead of prices is usually preferred, because their time-series properties
are easier to handle2 and because they are a natural measure of performance, which is essential in
portfolio allocation. We can now consider an investor who picks a bunch of n dierent securities
in which he wants to invest his wealth. Namely, he composes at time t 1 a portfolio p (with
value sp;t1 equal to his wealth) by combining those securities, e.g. buying Np
i;t1 shares3 of
security i to hold over the next period. At time t, the price of the securities have changed, and
the value sp;t and realized return rp;t of the portfolio are
sp;t =
Xn
i=1
Np
i;t1si;t;
rp;t =
sp;t sp;t1
sp;t1
=
Xn
i=1
Np
i;t1si;t1
| sp{;tz1 }
wp
i;t1
ri;t = w
p;t1rt; (2)
where we used vector notation for the portfolio weights wp;t1 =
wp
1;t1; ;wp
n;t1
and the
returns of the n securities rt = (r1;t; ; rn;t). The optimal allocation problem now consists in
a constrained expected utility maximization in order to

21. nd the optimal vector of weights wp;t to
hold over the next period. The expected utility is an investment criterion (e.g. maximize expected
2For example, they exhibit quasi-stationary patterns, whereas the prices often grow or decline over time.
3Np
i;t1 can be either positive or negative if one considers shorting the underlying security, that is borrowing it
from a broker and selling it naked, thus making a pro

22. t in case of falling price.

23. 6 Views Integration in Quantitative Portfolio Allocation
portfolio return, diversi

24. cation, Sharpe ratio, ...). It is usually represented by a utility function
U, which depends on both the weights and the joint distribution of the returns at t + 1. We use
probabilistic concepts because in practice it is (most of the time) impossible to know for sure the
future returns of a single security, let alone an entire basket of securities: there are unpredictable
events which forbid us to infer the future only from the past and the present, and even strategies
based on

25. xed income products4 such as bonds held until maturity suer from credit risk (e.g.
bankruptcies and other defaults events). In what follows, we require at least our strategy to be
self-

26. nancing, i.e. prices before and after re-balancing the portfolio have to be equal. We do not
consider non self-

27. nancing strategies (e.g. the optimal consumption/saving problem introduced
by Fisher in [31]) which need in general to be solved using dynamic programming (see [1] for an
introduction on the subject in Economics). In this respect, our minimal investment constraint is
Pn
called the budget constraint and is expressed as
i=1
wp
i;t = 1 8t.
1.2 The mean-variance allocation scheme
Let us give an example within the mean-variance framework pioneered by Markowitz in [45].
We start by assuming that an investor has originally picked the securities in which he wanted
to invest. Indeed Markowitz's framework (as other quantitative allocation schemes) was not
developed for stock picking (i.e. the initial choice of the n securities). In fact, themean-variance
oered the

28. rst rigorous approach to wealth allocation, but was by no means thought to help
selecting the investment universe. The expected utility criterion can be derived heuristically
by considering a second-order development of a generic (unspeci

29. ed) utility function U of the
portfolio return rp, that is
U (rp) U (0) +
@U
@rp

33. rp=0
rp +
@2U
@r2
p

37. rp=0
r2
p + O
r3
p
; (3)
with U (rp) 0. This development can indeed only be valid when considering small investment
horizons such as daily or weekly, that is horizons for which rp is (usually) close to zero. Truncating
the higher order terms, the expectation of equation (3) yields
E[U (rp)]
@U
@rp

41. rp=0
E[rp] +
@2U
@r2
p

45. rp=0
E
r2
p
; (4)
4Fixed income product are essentially a contract binding a borrower and a lender: in the simplest form, the
borrower receive a given amount of money when issuing the product, while committing himself to a string of future
periodic payments, with eventual repayment of the principal (original amount) at maturity. Bonds are example of
such securities, which oer return in the form of an interest rate.

46. Introduction 7
where we neglected the

47. rst term as the addition of a scalar plays no role in the expected utility
maximization (or the utility of zero return is zero). The truncation can by justi

48. ed for instance
in Gaussian markets when the whole distribution is characterized only by the

49. rst two moments,
provided a non-negative portfolio expected return5. Then only two economic assumptions
are needed: the rational investor prefers more to less and he is risk-averse6. While the

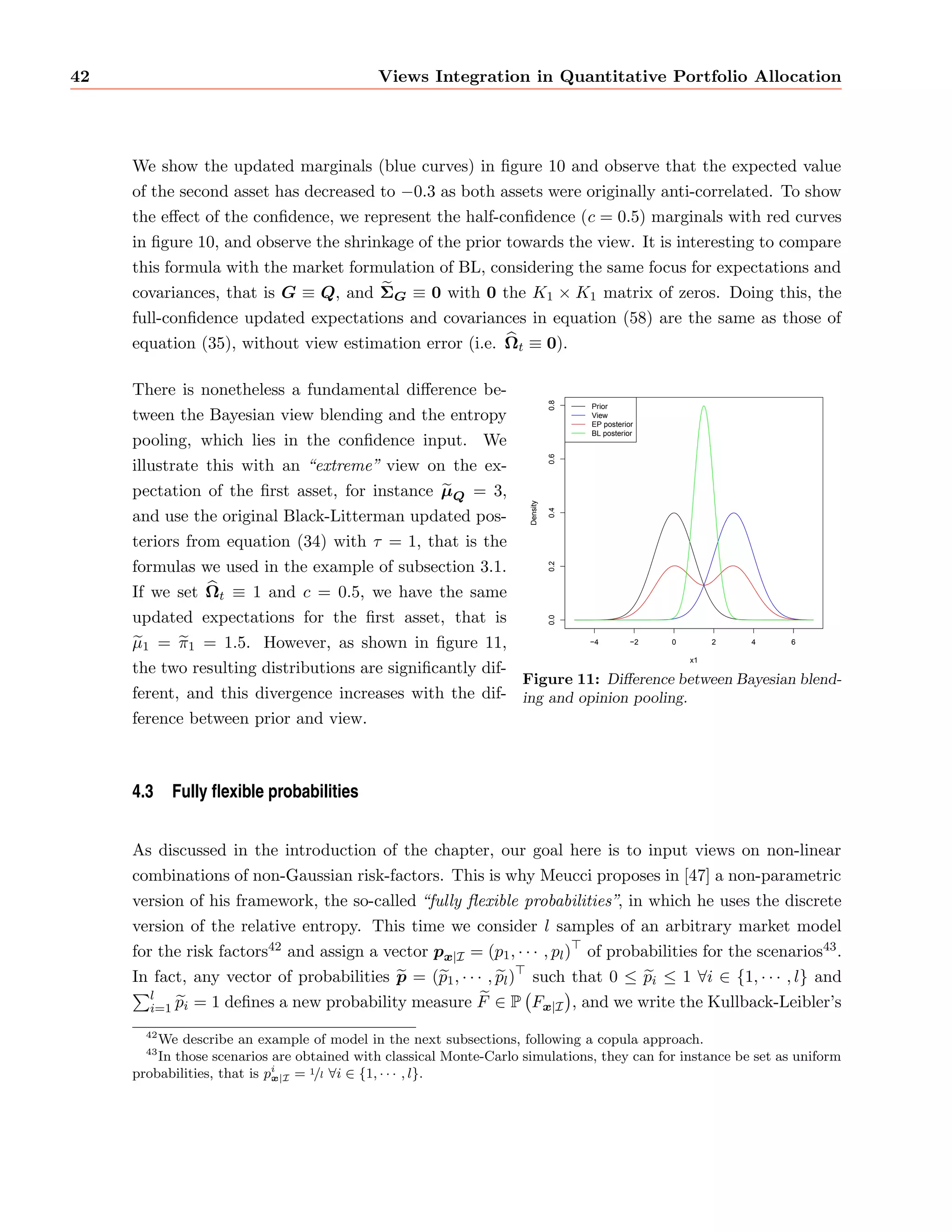
50. rst is
straightforward in the context of rational expectations, the second has been shown empirically
for instance in [54]. Those assumptions imply that the utility is an increasing function (or
equivalently the

51. rst derivative is positive) of the portfolio return, and moreover concave (i.e.
the second derivative is negative), which can be understood if one considers the squared return
as being a measure of dispersion, that is of market risk. More formally, we de

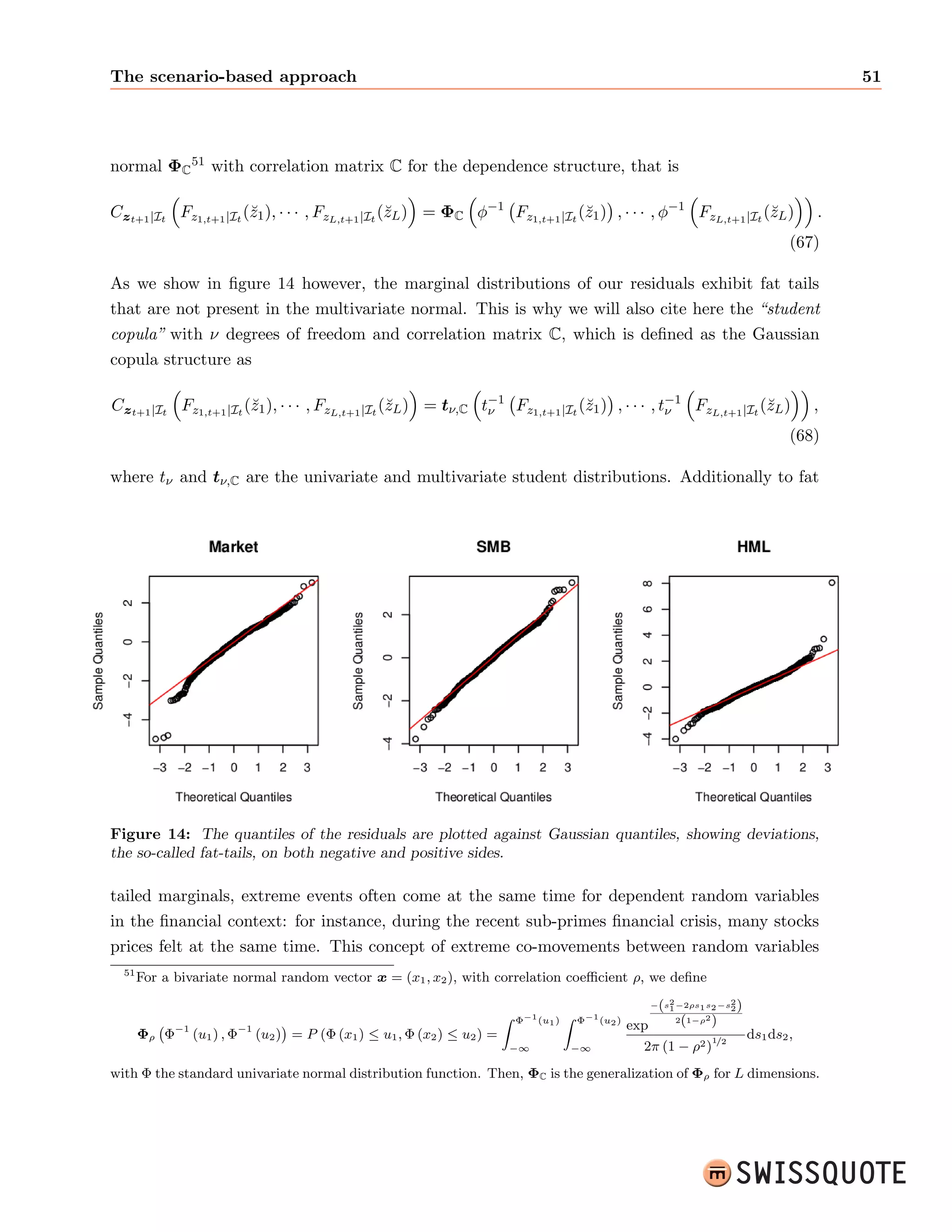
52. ne the vector
of conditional expectations t = (E[r1;t+1jFt] ; ;E[rn;t+1jFt]) and covariance matrix t
with ij;t = Cov [ri;t+1; rj;t+1jFt]7 for the individual securities at time t, where Ft denotes all
information available at that time, and jFt means conditional on the information set Ft8. Then
we have the portfolio conditional expected return
E[rp;t+1jFt] =
Xn
i=1
wp
i;t1E[ri;t+1jFt] = w
p;tt; (5)
which is the weighted average over the portfolio positions of the security conditional expected
returns, likewise the portfolio variance
V ar [rp;t+1jFt] = Cov
h
w
p;trt+1;w
p;trt+1jFt
i
=
Xn
i=1
wp
i;t
2
V ar [ri;t+1jFt] +
Xn
i;j=1;i6=j
wp
i;twp
j;tCov [ri;t+1; rj;t+1jFt]
= w
p;ttwp;t (6)
and the volatility [rp;t+1jFt] =
p
V ar [rp;t+1jFt] of the portfolio, with respect to the all infor-mation
available at time t. Finally the mean-variance expected utility, equivalently9 to (4), with
5If it was not the case, the investor would not bother optimizing.
6We de

53. ne the risk-averse investor as a rational investor who prefers the less risky when facing two opportunities
with equal expected payo.
7We de

54. ne the conditional covariance between two random variables ri and rj as
Cov [ri;t+1; rj;t+1jFt]= E [(ri;t+1 E [ri;t+1jFt]) (rj;t+1 E
[rj;t+1jFt]) jFt]. If ri = rj , we de

55. ne the condi-
tional variance V ar [ri;t+1jFt] = Cov [ri;t+1; ri;t+1jFt]= (ri;t+1 2 E
E [ri;t+1jFt])jFt
and conditional standard
deviation (also called volatility in our context) [ri;t+1jFt] =
p
V ar [ri;t+1jFt].
8We will give later a formal de

56. nition for the information set using the concept of

57. ltered probability space.
9The dierence comes from assuming that E [rp;t+1jFt]2 E
r2
p;t+1jFt
, or equivalently V ar [rp;t+1jFt]
E
r2
p;t+1jFt
.

58. 8 Views Integration in Quantitative Portfolio Allocation
risk-aversion parameter
reads
E[U (wp;t;t;t)] = E[rp;t+1jFt]
2
V ar [rp;t+1jFt]
= w
p;tt
2
w
p;ttwp;t: (7)
The risk-aversion parameter
=
1
2
@2U
@r2
p

61. rp=0
@U
@rp

64. rp=0
; (8)
which represents a trade-o between the expected performance of the portfolio and its associated
uncertainty, is assumed to be chosen before the optimization and then constant over the holding
period. With the additional budget constraint and dropping the subscripts t and p for simplic-ity,
the optimization problem of

65. nding the optimal w can be formulated as the Lagrangian
maximization
(w; ) argmax
w;
fL (w; )g ;
L(w; ) = w
2
ww
w1 1
; (9)
where we added the Lagrangian multiplier and 1 is a vector ones. The

66. rst-order conditions
@L(w; ) =@wjw; = 0 and @L(w; ) =@jw; = 0 yield the optimal weights of the portfolio
w
!
=
1
1 0
!1
1
!
: (10)
which corresponds to a global maximum of 9 provided is positive de

67. nite. The set of values
for
2 (0;1) induces a set of attainable portfolios de

68. ning the so-called the (mean-variance)
ecient frontier, that is all the portfolios a rational investor could invest in given the infor-mation
available at time t. This is illustrated in

69. gure 1 for a simple two-asset case. For an
investor with low risk-aversion (say
1), the expected utility maximization only consists
in maximizing the expected performance of the portfolio. Thus, the investor would hold short
as much as possible securities with lowest expected returns and hold long as much as possible
securities with maximal expected return. On the contrary with a large risk-aversion, expected
performance becomes negligible with respect to market risk, and the investor will hold a portfolio
with minimal volatility.

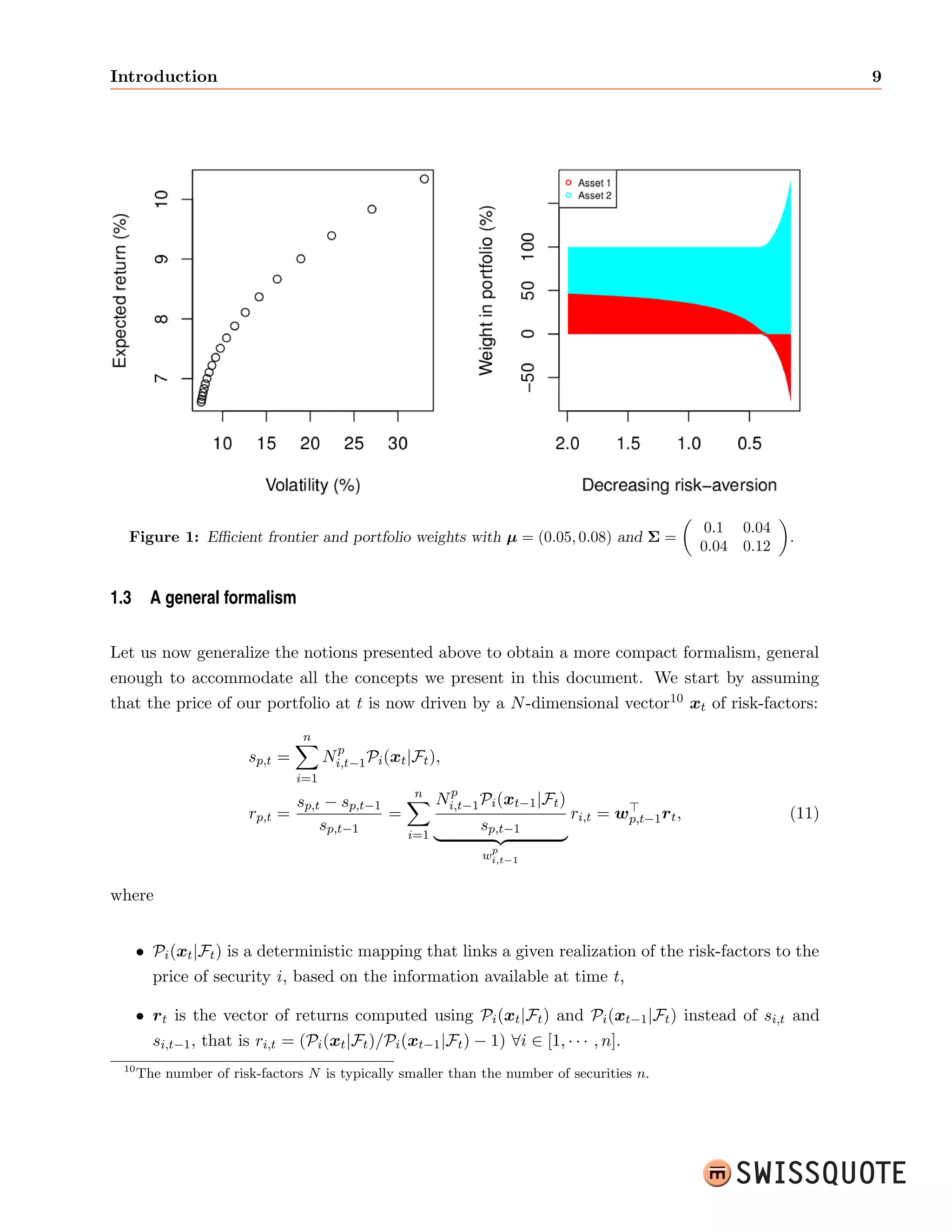
70. Introduction 9
Figure 1: Ecient frontier and portfolio weights with = (0:05; 0:08) and =
0:1 0:04
0:04 0:12
.
1.3 A general formalism
Let us now generalize the notions presented above to obtain a more compact formalism, general
enough to accommodate all the concepts we present in this document. We start by assuming
that the price of our portfolio at t is now driven by a N-dimensional vector10 xt of risk-factors:
sp;t =
Xn
i=1
Np
i;t1Pi(xtjFt);
rp;t =
sp;t sp;t1
sp;t1
=
Xn
i=1
Np
i;t1Pi(xt1jFt)
| sp{;tz1 }
wp
i;t1
ri;t = w
p;t1rt; (11)
where
Pi(xtjFt) is a deterministic mapping that links a given realization of the risk-factors to the
price of security i, based on the information available at time t,
rt is the vector of returns computed using Pi(xtjFt) and Pi(xt1jFt) instead of si;t and
si;t1, that is ri;t = (Pi(xtjFt)=Pi(xt1jFt) 1) 8i 2 [1; ; n].
10The number of risk-factors N is typically smaller than the number of securities n.

71. 10 Views Integration in Quantitative Portfolio Allocation
For example, if stock i belongs to the portfolio, it is customary to take (at least) its return as
a risk factor (i.e. xi;t = ri;t), and we have Pi(xtjFt) = si;t1(1 + xi;t) (with si;t1 the price at
t1). In general, risk-factors may be the returns of individual securities, but could also include
market/sector indices, FX rates, sovereign yield curves, macroeconomic indicators, etc. While
the pricing function may not depend on the other securities, one should not mistake it for an
independence hypothesis between the risk-factors, as these are usually not independent. For
example, in the simple case described above (with only the returns of the individuals securities
as risk-factors), the pricing function of each security only depends on one risk-factor, whereas
it is well known that asset returns are correlated (e.g. between securities of the same country
or industry sector). In the remainder of the document, we will refer to the risk-factors as the
random vector driving a so-called market model. We emphasize that the description oered by
the risk-factors that one chooses can often be applied to a dierent and broader market than the
investment universe. Then, a historical observation corresponds supposedly to a realization of
the market model, which we will now formally de

72. ne. Let (
x;F; Px) be the

73. ltered probability
space for the market model driven by our vector x of N risk-factors, with
a set of possibles outcomes
x =
x1
xN RN for the random vector x,
a

74. ltration (i.e. a sequence of sv-algebras fFtgt0, Ft F 8t) representing all the informa-tion
available at time t,
a probability measure Px where Px (!) denotes the (unconditional) probability of the out-come
! 2
x.
For (x1; ; xN) 2
xt+1jFt , the distribution function
Fxt+1jFt (x1; ; xN) = Pxt+1jFt (x1;t+1 x1; ; xN;t+1 xN) (12)
denotes the probability of the joint event (x1;t+1 x1; ; xN;t+1 xN) given the information
available at time t. Conversely, it may also be convenient to use the survival distribution, which
can be de

75. ned as
Fxt+1jFt (x1; ; xN) = Pxt+1jFt (x1;t+1 x1; ; xN;t+1 xN) ; (13)
that is the probability of the joint event (x1;t+1 x1; ; xN;t+1 xN) given the information
available at time t. For simplicity, we will assume
xt+1jFt = RN at all times, even if this is not
realistic11. Keeping in mind that 1 should be inf
xi;t+1jFt and 1 should be sup
xi;t+1jFt for
11Take for example xi as the return on a stock, then a realization xi;t = 1 means that the company went
bankrupt and therefore yields
xi;t+1jFt = f0g.

76. Introduction 11
all i 2 f1; ;Ng, the joint probability density, if it exists, is the function f :
xt+1jFt ! R
such that
Fxt+1jFt (x1; ; xN) =
x1
1
xN
1
fxt+1jFt (x1; ; xN) dx1 dxN (14)
for all (x1; ; xN) 2
xt+1jFt . If this function exists, Fxt+1jFt is said to be absolutely continu-
ous. For all i 2 f1; ;Ng and xi 2
Xi;t+1jFt , we can also de

77. ne the marginals as
Fxi;t+1jFt(xi) = Fxt+1jFt(1; ; xi; ;1); (15)
1
fxi;t+1jFt(xi) =
1
1
1
fxt+1jFt(x1; ; xi; ; xN)dx1 dxN; (16)
where Fxi;t+1jFt(xi) = Pxt+1jFt (xi;t+1 xi) and the joint density in the third equality is in-tegrated
over all variables but xi. Indeed, one can also de

78. ne the marginals for the survival
distribution as Fxi;t+1jFt(xi) = Fxt+1jFt(1; ; xi; ;1) = Pxt+1jFt (xi;t+1 xi) for all
i 2 f1; ;Ng and xi 2
Xi;t+1jFt . From now on, we will only consider absolutely continuous
distributions and denote xt+1jFt fxt+1jFt . If we knew this probability density, the optimal
allocation would be
w
p;t argmax
wp;t2C
E
U(wp;t; fxt+1jFt)
; (17)
where C is the set of investment constraints and E[U] the expected utility function to maximize.
As one may have guessed, in practice, an investor never accesses the complete information set
Ft. Let us denote It the information set publicly available12 8t. Requiring the property It Ft
8t means that the public information available to most investors represents only a subset of the
complete information. For example, consider a

79. rm whose quarterly results announcement is
expected at time t + 1. Then at time t, corporate insiders such as the Executive Management
already know the quarterly results and thus have an extended information set Jt, which reads
formally It Jt Ft. We often still need the second inclusion because insiders are not om-niscient
(e.g. they always lack some internal or external private information). However, the
complementary information set (that is the information set Bt such that Jt
S
Bt = Ft) may also
be of negligible importance or irrelevant in the sense Fxt+1jJt Fxt+1jFt , and we will denote
equivalently in this case Jt Ft. This discussion is closely related to the classical problems of
market eciency andasymmetric information in Economics and contract theory, but we shall
leave this aside for now and give more details about these concepts and their link to dierent
information sets and market views later in the document. Before we introduce the problem of
12More details will be given on the precise meaning of publicly available in the context of market views.

80. 12 Views Integration in Quantitative Portfolio Allocation
market views, we assume that our investor has an incomplete information set, for instance It, to
model the distribution of future returns. Then we will explain how it is possible to incorporate the
investors private information Jt to model the market distribution conditional on (It [ Jt) Ft
8t. In what follows, we recall succinctly the problem of dimension reduction and (linear) factor
models, because these notions are necessary here for two reasons:

81. rst they form the basics of
equilibrium pricing theories that are needed in the Black-Litterman model, and second because
appropriately chosen factors allow to model a market of large size in a parsimonious way.
1.4 Dimension reduction and linear factor models
Portfolios are often composed of hundreds of securities, but the data available to model them
are usually limited to empirical time series ranging from a few hundred to a few thousand
observations. In the equity case, this consists in a lot more data than the one available to model
credit default events for instance, but it is still often insucient to model directly the whole joint
distribution. Dimension reduction is thus an essential concern both in academic and applied
research. Furthermore, many alpha-generating13 strategies are based on exposure to exogenous
factors such as market indices, growth of industry sectors, or evolution of exchange rates. As
practitioners often have views related to those exogenous factors, this also explains why they are
commonly used to model large investment universes.
The purpose is to write the N-dimensional vector of risk-factors x as a N 1 function14 g :
RL ! RN of a L 1 vector y = (y1; ; yL)of L N (or possibly L N) factors. In full
generality, any kind of factor model reads
x = g (y) =
0
g1 (y1; ; yL)
...
BB@ gN (y1; ; yL)
1
CCA
: (18)
There are dozens of techniques used in various scienti

82. c

83. elds, but there exists basically two
approaches in

84. nance: the statistical techniques and economically motivated equilibrium pricing
theories. For example, the Principal Component Analysis (PCA, see [46] for details) may be the
most widely used in the

85. rst category, whereas for the second, the Capital Asset Pricing Model
or the more recent Arbitrage Pricing Theory (CAPM and APT, see [26] for example) are now
standard in most

86. nance textbooks.
13The alpha is a measure of a risk-adjusted return on an investment. To generate alpha means to generate
abnormal (usually positive) returns compared to that of the market.
14As mentioned in subsection 1.1 for the risk-factors, the support and image of g are most of the time restricted
to smaller subsets of L R
and NR
.

87. Introduction 13
In many cases, one assumes a linear relationship between the original risk-factors and the new
set of factors, which can be interpreted as a

88. rst order Taylor polynomial approximation of g
(more likely in low-volatility periods) for small realizations of y. Thus we write
0
BB@
x1
...
xN
1
CCA
=
0
BB@
g1 (y)
...
gN (y)

96. 1
CCA
y=0
+
0
BB@
@g1
@F1
(y) @g1
@FL
(y)
...
. . .
...
@gN
@F1
(y) @gN
@FL
(y)
1
CCA

104. y=0
0
BB@
y1
...
yL
1
CCA
+
0
BB@
1
...
N
1
CCA
; (19)
where we added a vector of residual errors = (1; ; N). In matrix form, this expression for
the risk-factors at time t reads
xt = a + Byt + t; (20)
where a is a N 1 vector of constants and B is a N L matrix of exposures to the factors.
Byt represents the systemic part of the returns (i.e. typically depending on the market), while
t is called the idiosyncratic part. The most commonly used technique to decompose xt as in
equation (20) is an OLS regression on exogenously-speci

105. ed factors (for example the returns of
a market index in case of the CAPM) or endogenous factors (e.g. using statistically de

106. ned
factors as the eigenvectors of the sample correlation matrix of x). For any sample period ]t T; t[
used to estimate a as ba
and B as bB
, where the subscript bx will from now on be used to denote
an estimator of the quantity x, the OLS regression provides the following important result
dCov [yijjIt] = bE
[j;t+1jIt] = 0 8i 2 f1; ;Lg and 8j 2 f1; ;Ng : (21)
In theory,

107. nding factors such that Cov [ijjIt] = 0 8t, 8i 2 f1; ;Lg and 8j 2 f1; ;Ng
(that is

108. nding a set of factors such that the idiosyncratic parts are uncorrelated) would be
very convenient, because one could then model the factors yt+1 fyt+1jIt on their probability
space (
y; I; Py), which is easier than modeling xt+1 fxt+1jIt as L N. Then, one would
only need to model univariate marginals i;t+1 fi;t+1jIt on their probability space (
i ; I; Pi)
8i 2 f1; ;mg to retrieve xt+1 fxt+1jIt . In practice however dCov [ij ] = 0 is never achieved15,
but we usually have dCov [ijjIt] dCov [xixjjIt] if the factors are appropriately chosen. Then
it is common practice to consider the residuals as uncorrelated. If additionally the marginals
are close to Gaussians, it is convenient to model them as independent random variables, that is
t+1 f1;t+1jIt fN;t+1jIt . We leave further consideration on the factor dependence structure
for the subsection 4.5, where we present a complete market model, and give now a practical and
15Correlated errors can be handled by Generalized Linear models, at the cost of the handy OLS property from
equation (21).

109. 14 Views Integration in Quantitative Portfolio Allocation
important example of linear factor model.
1.5 The Fama–French three-factor model and market benchmarks
A widely used factor model in

110. nance is the Fama{French three-factor model [28, 29]. Fama,
E. and Eugene, F. started with the CAPM, which uses one market factor to characterize (in
sample) about 70% of the variability of stocks returns in the U.S. equity universe. Through
research, they were able to identify that portfolios composed of small-cap and high book-to-market
ratio stocks (the later are called value stocks) have a higher expected return than those
composed of large-cap and small book-to-market ratio stocks (the later are calledgrowth stocks).
This lead them to a model explaining more than 90% of the variability of U.S. stock returns with
two additional factors added to the market factor: the small minus big factor (the average
return of portfolios composed of small cap stocks minus the average return of portfolios composed
of large cap stocks) and the high minus low factor (the average return of portfolios composed
of high book-to-market stocks capitalization minus the average return of portfolios composed of
small book-to-market stocks). For more details about the construction of the factors, we refer to
appendix A.
As an example of how to use the three factors and more generally throughout the whole document,
we use a set of the 673 weekly prices than 303 stocks traded on the New-York Stock Exchange
(NYSE) between January 1999 and December 201116. The whole U.S. market is much wider that
303 stocks, so it is important to compare our universe to the whole market in order to detect
possible statistical biases. Furthermore, in the context of portfolio allocation, it is necessary
to test our allocations against appropriate benchmarks. The literature on the subject is very
rich, and among general characteristics (see [5] for example), we require a few attributes for our
benchmark portfolios:
Investible: we should be able to invest in all the securities.
Appropriate: our benchmark has to be relevant to our investment strategy.
Unambiguous: our benchmark has to be unambiguous in the sense that it is perfectly
de

111. ned at all times without an optimization process.
16Incidentally, this choice corresponds to the part of the U.S. stock universe in which on can invest through
Swissquote's electronic asset management engine, or ePB from now on.

112. Introduction 15
The simplest example of benchmark is an equally-weighted benchmark, that is a portfolio with
weights we
i;t = 1=n 8i and 8t. However, tracking this benchmark can generate very high trans-action
costs as one needs to constantly re-balance all positions in portfolio, selling winners and
buying losers to maintain equal weights17. Furthermore, giving the same importance in our
benchmark to very small or large companies may not be a good proxy for the market portfo-lio.
In what follows, we will consider wmt
a capitalization-weighted benchmark on the universe,
de

113. ned by weights
wm
i;t =
Pmi;t n
i=1mi;t
; (22)
where mi;t is the market capitalization of security i at time t. In

114. gure 2, we show the normalized
2000 2002 2004 2006 2008 2010 2012
0.8 1.0 1.2 1.4 1.6
Normalized value
US market
Cap−weighted benchmark
Figure 2: The Fama-French market factor and our universe's benchmark
value of our benchmark against the market factor of Fama and French. It should be noted that
this factor is in fact a capitalization weighted benchmark of the whole US stock market, to which
we will simply refer as the market from now on. We observe that they show similar patterns,
but that the

115. nal performance of our benchmark over the sampling period is 64%, whereas that
of the whole US stock market is only 44%. It can mainly be explained by a survivor bias,
in the sense that our universe is only composed of stocks that were not delisted during the
17Hence the equally-weighted is a contrarian strategy.

116. 16 Views Integration in Quantitative Portfolio Allocation
Name Mean Std Dev Min Max t-stat
Intercept 0.002 0.002 -0.002 0.008 15.855
Market 0.990 0.367 0.217 1.935 -0.454
SMB 0.002 0.344 -0.700 1.379 0.121
HML 0.303 0.579 -2.086 1.809 9.107
Table 1: Summary statistics for the Fama-French factor model. For the market factor, the t-stat is
computed with the null hypothesis that the true mean is 1, whereas the null is that the mean equals 0 for
the other coecients. As the degree of freedom is 302, the 95% critical value is 1.650.
sampling period, hence yielding an upward bias in their performances. In table 1, we present
summary statistics for the coecients obtained by an OLS regression of the Fama-French factors
on our stock universe. We observe that our mean intercept is small, but signi

117. cantly dierent
from 0, which is another evidence of the survivor bias in our universe. As expected, the mean
exposure to the market is 1 (and this hypothesis cannot be rejected at the 95% con

118. dence level).
Furthermore, our universe does not appear either upward nor downward market cap biased (as
we cannot reject the hypothesis that the mean of the exposure to the SMB factor is dierent from
zero at the 95% con

119. dence level), but we still observe a signi

120. cant upward book-to-market bias.
o
o
N(0,1)
Original data
Residuals from model
−5 0 5 10 15 20
0.0 0.1 0.2 0.3 0.4
Rescaled correlation
Density
llllllllll
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lllllll lll llllllllllllll
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
lllllllllllllllllllllllllll
Figure 3: Density of rescaled correlations.
Because of the two upward biases, we can
expect portfolios composed of stocks in this
universe to have signi

121. cantly greater returns
than portfolios composed of all US stocks, and
thus we need to be careful with any conclusion
about performances in the context of portfo-lio
allocation. To evaluate graphically if the
dependence between the securities was cap-tured
by the model, we show the distribution
of correlations b [ri; rjjIt] and b [i; jjIt] in

122. g-ure
3, where we rescaled the correlations by
the square-root of the number of observations
(weeks) in the sample. If the data (or the
residuals) were uncorrelated, then the corre-lations
should follow a standard normal distri-bution.
We observe that most of the (linear)
dependence between the returns is captured
by our model (the mean correlation is reduced from 0.278 to 0.026), but that there is still a
large positive skew in the distribution. This can mainly be explained by the fact that the model
fails to capture the dependence between highly correlated stocks (the largest coecient is only

123. Quantitative integration of market views 17
reduced from 0.853 to 0.719). However, because the proportion of correlation coecients higher
than 0.25 is still reduced from 57% to 2%, the model does well at capturing the overall (linear)
dependence. We will refer to this three-factor model several times during the remainder of the
thesis and leave it aside for now.
2 Quantitative integration of market views
Since the path-breaking approach of Black and Litterman in 1992, academics and practitioners
proposed various methods in order to modify quantitative allocations according to investors
having a particular perception of future market conditions. The precedent chapter was dedicated
to recalling the basics in quantitative portfolio allocation and setting the frame for the next
stage. On the other hand, this chapter is devoted to present the necessary economic notions
for the integration of market views, and as well as their formalization and incorporation in the
quantitative framework we exposed.
2.1 Information sets, efficient market hypothesis and market views
As we mentioned in the introduction, there is an in

124. nite number of distinct informations sets,
but they are not all relevant in the context of portfolio allocation. We will make now a distinction
between three subsets (or class of subsets) of Ft:
The set Kt composed of all the information contained in past securities prices until time t,
that is mainly time series of prices, volumes and all data used in technical analysis.
The set It, with Kt It, composed of all information publicly available at time t, that is
the information contained in Kt as well as fundamental and contemporaneous information
which may impact present prices (such as newspapers, informations from a provider like
Bloomberg or Reuters, and so on).
All the sets Jt, with It Jt, composed of private information at time t. As opposed to
It and Kt, Jt is not unambiguously de

125. ned, because each market participant may have his
own Jt.
While the two

126. rst sets are fairly straightforward, Jt may be slightly more complicated to grasp.
For example, there are many sets Jt on which investors cannot legally make pro

127. ts, the so-called
material non-public information (for example the balance sheet of a company before it

128. 18 Views Integration in Quantitative Portfolio Allocation
is made public), because of laws forbidding insider trading. However, the concerned corporate
insiders still trade while possessing superior private information (e.g. a CEO may to some extent
buy shares of his

129. rm to inspire con

130. dence on pro

131. tability to come). While some investors
believe that those trades yield valuable information (i.e. allowing them to generate abnormal
returns compared to that of the market), academic studies [43, 35, 30, 58, 41, 37] have provided
mixed evidence for this hypothesis. Because these trades are reported to regulators and then
publicly disclosed, we will still consider them as part of It. Nonetheless, investment banks and
brokerage houses spend a huge amount of money on analysts covering companies, which would
probably not be the case if they couldn't obtain some valuable information. Some may counter
this reasoning arguing that they mainly provide a service to please their clients, meaning that
their so-called coverage does not yield valuable information. For studies on the pro

132. tability of
institutional analyst recommendations, we refer for example to [6, 7, 36, 8] (even though the
literature on the subject is very rich and de

133. nitely not limited to these papers). As for the
potential mistakes in these studies because of database ex-post manipulations, they were

134. rst
documented in [42].
As mentioned in the introduction, the concept of dierent information sets is closely linked
with the concept of ecient-market hypothesis (thereafter EMH) which is a central concept
in portfolio allocation and a pillar of the Black-Litterman model that we will describe later in
this chapter. This hypothesis was developed by Fama in [27] and describes what information
one could use to beat the market (or yield abnormal returns) with temporal regularity (i.e.
consistently over time).
But

135. rst things

136. rst: what is the market? It is mostly a theoretical concept based on the as-sumption
that assets are in

137. nitely divisible: the market portfolio is usually de

138. ned as a weighted
bundle of all assets investible, and the US market factor of Fama and French is merely a proxy
for the US stock market. The market can be de

139. ned in many ways, for example it could also be
a known market index, or a weighted benchmark over several asset classes (such as

140. xed income,
commodities, etc). While it is fairly complicated to identify the market portfolio, a recent study
on the control network of transnational corporations [59] suggests that the so-called market
portfolio may consist of far less assets (a core of 147

141. rms) than commonly believed (as global
indices count several hundreds of even thousands of assets). In this document, we only consider
that the stock market portfolio, represented by the market factor of Fama and French, exists
and assume its historical prices available in order to perform various estimations. Then, the
ecient-market hypothesis exists essentially in 3 (sometimes not so clearly) distinct forms18:
18Here we consider Jt as the set of all relevant private information in the sense described in the

142. rst chapter,
that is the set such that for Lt with Lt
S
Kt = Ft, we have Fxt+1jJt Fxt+1jFt or equivalently Jt Ft.

143. Quantitative integration of market views 19
The strong form implies that all public and private information is instantaneously re-
ected in security prices. With our formalism, it means that Kt It Jt Ft, or
equivalently Fxt+1jKt Fxt+1jIt Fxt+1jJt Fxt+1jFt . It means that one cannot hope to
optimize portfolio allocation in order to beat the market, even using private information,
as it is already priced.
The semi-strong form implies that only public information is instantaneously re
ected in
security prices. We will denote it Kt It Jt Ft, or equivalently Fxt+1jKt Fxt+1jIt6=
Fxt+1jJt Fxt+1jFt . It means that in possession of private information, one could optimize
portfolio allocation in order to beat the market by having more information about the
distribution of future returns, but that all public information is already priced19.
The weak form implies that only the information from past prices is re
ected in present
prices. We will denote it Kt It Jt Ft, or equivalently Fxt+1jKt6= Fxt+1jIt6=
Fxt+1jJt Fxt+1jFt . With this form of eciency, one could improve optimization in order
to beat the market by both including contemporaneous (e.g. fundamental) and/or private
information20.
With this de

144. nition, ineciency represents the case where it is possible to yield abnormal returns
by using past prices (for example patterns in price changes). While academics found evidence
in favor and disfavor of each of the forms in thousands studies published during 50+ years, or
criticized them in the context of behavioral

145. nance or the recent

146. nancial crisis21, the only con-sensus
is the rejection of the strong form because of frictions slowing the diusion of private
informations22 and practice (i.e. the real world) is indeed quite dierent. We've already cited
investment banks and brokerage spending money on analysts coverage as well as investors believ-ing
in following corporate insider trades, but there are plenty of other examples of practitioners
rejecting market eciency. For example, technical analysts have made a profession capitalizing
on (their belief in) complete market ineciency, looking for patterns in prices. Furthermore,
the whole hedge fund industry is based on the belief that skilled people are able to generate
(consistently over time) abnormal returns.
19Investors believing in the pro

147. tability of following corporate insiders trades make in fact the hypothesis that
the market is not semi-strongly ecient (or weakly, or not at all).
20Investors believing in analyst recommendations and coverage from investment banks make in fact the hypoth-
esis that the market is only weakly ecient (or not ecient at all). However, it could sometimes appear more
like insider trading: the market could be semi-strongly ecient, but investment bankers would advise their client
with a private information set Jt with It Jt (for instance during Facebook's IPO) allowing for abnormal pro

148. ts.
21As the subject is standard in the most basic economics textbooks and because entire books have been written
only on the hypothesis, we feel that a long list of references would not provide added value to this document.
22The laws preventing insider trading are in fact barriers for private information to become public and priced
instantaneously.

149. 20 Views Integration in Quantitative Portfolio Allocation
eE
In what follows, we consider the market to be semi-strongly ecient for the sake of simplicity23,
but most of what we present can be (and actually is) applied to weakly or inecient markets.
We capitalize on the belief that practitioners daily engaged in the market often have a particular
perception of its future evolution. In fact, we will only assume that asymmetry of information24
do exist, that is It Jt Ft for an investor with his own private set Jt6= It. For example,
this investor could forecast a large positive jump in the price of stock i over the next investment
period, which would read [ri;t+1jIt;Jt] bi;t. Note that, as we choose to use bx for the
estimator of the quantity x, the subscript ~x is from now on used for the investor's market views
on the quantity x, sometimes dierent from bx. In this case, the view is assumed dierent from
any estimator of future performance bE
we would use if we only looked at past realizations of
the risk-factors or using all publicly available (included fundamental) information. Furthermore,
this view might also come with a con

150. dence (i.e. the fact that investors are rarely 100% certain
about their views, except for above-mentioned illegal insider trading).
2.2 Problem formalization
Given that information asymmetry exists, we introduce formally in this subsection what it implies
in the context of portfolio allocation. We describe qualitatively how this asymmetry can (and
should) be taken into account by a savvy investor to optimally allocate his portfoliok, given
the information at his disposal. As discussed in the introduction, assuming the reference model
xt+1 fxt+1jFt for the joint density of our N risk-factors to be known, the optimal allocation at
t reads
w argmax
w2C
E
U(w; fxt+1jFt)
; (23)
where C is the set of investment constraints and E[U] the expected utility function to maxi-mize.
Unfortunately, an investor can only use an estimated distribution inferred from the pub-lic
information set, which we assumed incomplete, for the optimal allocation, that is he uses
b fxt+1jIt6= fxt+1jFt to obtain
bw
argmax
w2C
E
h
U(w; b fxt+1jIt)
i
6= w: (24)
It is straightforward to understand this in presence of asymmetric information, but there is
another interpretation even in a perfectly ecient market: Bayesian principles state that even
23To be completely honest, another reason is historic, in the sense that it was the academic consensus when
Black-Litterman proposed their original model.
24Here, we only mean that all relevant information is not already priced.

151. Quantitative integration of market views 21
with Kt It Jt Ft, we would still base our estimation b fri;t+1jFt of the true density fri;t+1jFt
using a sample of

152. nite size, thus inducing an estimation error.
As an investor may detain a private information set Jt, re
ecting his own perception of future
market evolutions, the goal of market-views integration methods is to incorporate this new in-formation
set in the estimated distribution for the risk-factors. Let us go back to our simple
mean-variance two-asset example and assume that the investor believes in his variance forecast
statistically inferred from the publicly available information. Assume now that he believes that
the company whose stock represents the second asset may soon announce lower than expected
earnings, changing his forecast to an expected return of 6% from the initial 8%. We represent
the ecient frontier and portfolio weights in

153. gure 4, where we observe that optimal portfolios
contain more of the

154. rst asset for all risk aversions, but that the dierence decreases while we
increase the risk aversion, because the risk has more and more impact (and the forecast has not
been modi

155. ed).
l
l
l
l
l
llll
l
l
l
l
l
l
l
l
l
l
l
10 15 20 25 30
7 8 9 10
Volatility (%)
Expected return (%)
2.0 1.5 1.0 0.5
−50 0 50 100 150
Weight in portfolio (%)
Decreasing risk−aversion
l
l
Asset 1
Asset 2
l
l
l
l
l
llll
l
l
l
l
l
l
l
l
l
l
l
7.5 8.0 8.5 9.0 9.5 10.0
5.5 5.6 5.7 5.8
Volatility (%)
Expected return (%)
2.0 1.5 1.0 0.5
0 20 40 60 80 100
Weight in portfolio (%)
Decreasing risk−aversion
l
l
Asset 1
Asset 2
Figure 4: Ecient frontier and weights,

156. rst with b
= (0:05; 0:08) and then with b
= (0:05; 0:06).

157. 22 Views Integration in Quantitative Portfolio Allocation
Furthermore, we observe that as the dierence in expected returns between the assets has been
reduced, the increase in utility coming from buying more of asset 2 than asset 1 is smaller for
the same risk-aversion parameters, which leads to more diversi

158. ed and less volatile portfolios.
In

159. gure 5, we show realized returns both sets of portfolios for various scenarios. First, we
Figure 5: Realized returns with the initial allocation in blue and the one modi

160. ed by the view in red.
On the left, the circles are for asset returns of (0:06; 0:07) and triangles for (0:07; 0:06). On the right, the
circles are for asset returns of (0:07;0:06) and triangles for (0:06;0:07).
observe that, because the weights are almost the same for high risk aversions the returns are
also very close, but the dierence increases dramatically when we decrease risk aversion and give
more importance to performance forecasts. Second, we observe that the second set of portfolios
outperform the

161. rst set when the

162. rst asset outperforms the second as expected, and that this
dierence also increases as we give more importance to return forecasts.
2.2.1 Views focus
In our optimal allocation framework, K views may then be K statements made on K generic
functions of the risk-factors. At time t, those functions, the so-called focus of the views, can be
represented as a K 1 function of a N 1 random vector xt = (x1;t; ; xN;t)of risk-factors,
which we can write v : RN ! RK
vt v (xt) =
0
BB@
v1 (x1;t; ; xN;t)
...
vK (x1;t; ; xN;t)
1
CCA
; (25)

163. The Black-Litterman model and extensions 23
where, as for g in (1.4), the support and image of v are most of the time restricted to smaller sub-sets
of RN and RK. The estimated distribution of this new random vector over the next period
inherits the (estimated) distribution of the reference model, and we will write vt+1 b fvt+1jIt .
Then the most detailed view would be the speci

164. cation of a complete new distribution e fvt+1jIt;Jt
for the focus, that is by writing vt+1 e fvt+1jIt;Jt6= b fvt+1jIt . However, views are more often
statements on speci

165. c features of the distribution of the focus (e.g. low-order moments, or more
generally any measure of location, scale or dependence). For example, one could input views on
expectations eE
(vk;t+1jIt;Jt) S mk or volatilities e (vk;t+1jIt;Jt) S k, for a speci

166. ed mk, respec-tively
k representing the view of the investor. An investor may have a qualitative ranking view,
e.g.

167. nancials will outperform industrials, like eE
(vi;t+1jIt;Jt) : : : eE
(vk;t+1jIt;Jt). Fur-thermore,
one may want to input views on correlations (via the speci

168. cation of a new correlation
matrix e C(vt+1)) e.g. to perform stress-tests. Finally, one may have a view on the lower (upper)
tail behavior (via the speci

169. cation of a new quantile eQ
vt+1(u) for a tail level u) or co-dependence
(via the speci

170. cation of a new copula of vt+1, e Cvt+1(u) at joint threshold levels u).
2.2.2 Views integration
The goal is to

171. nd a way to take these views into account in order to obtain the new distribution
of the focus and infer e fxt+1jIt;Jt6= b fxt+1jIt for the risk-factors. Once this new distribution is
known, the optimal portfolio allocation becomes
w argmax
w2C
E
h
U(w; e fxt+1jIt;Jt)
i
: (26)
To infer the new distribution, scholars have followed various approaches. It started, as often in
quantitative

172. nance, by considering a Gaussian market at equilibrium. Using Bayesian inference,
the Black-Litterman model and extensions provide analytical formulas that represent the

173. rst
mathematically sound way of modifying forecasts in the scheme developed by Markowitz. With
the next chapter, we enter the heart of the project by describing this method, giving numerical
illustrations at every step.
3 The Black-Litterman model and extensions
What is the Black-Litterman (BL) model about? A nice answer starts by quoting the conclusions
of Markowitz in his seminal paper of 1952:

174. 24 Views Integration in Quantitative Portfolio Allocation
My feeling is that statistical computations should be used to arrive at a tentative set of these
i and ij . Judgment should then be used in increasing or decreasing some of these i and
ij on the basis of factors or nuances not taken into account by the formal computations. [...]
One suggestion is to use the observed i, ij for some period of the past. I believe that better
methods, which take into account more information, can be found. I believe that what is needed
is essentially a probabilistic reformulation of security analysis. I will not pursue this subject
here, for this is another story.
In 1990 and 1992, Black F. and Litterman R. proposed the now called Black-Litterman model,
published

175. rst in Fixed Income Research of Goldman Sachs and in the Financial Analysts
Journal in their path-breaking articles [10] and [11], to address at least two of the issues raised
by Markowitz. First, BL capitalizes on a prior estimate of market consensus for a security's
expected return (the i) to regularize Markowitz's mean-variance. Second, it oers a sound way
of modifying these expected returns and the covariances25 with respect to more information,
that is the private information set.
3.1 First pillar: a Gaussian market
In the original approach, the risk-factors are the security excess returns over the risk-free rate26
(xi;t ri;t rf;t 8i 2 f1; ; ng and 8t). Given all available public information, we consider a
multivariate Gaussian distribution for the reference model, that is
xt+1jIt N(tjIt ;b
t); (27)
where b
t is an estimator of t. Furthermore, we assume that the risk in the reference model,
represented only by b
t in a Gaussian market, was estimated without error (or merely that it is
negligible compared to the error on the expected return). However, in a Bayesian framework, we
assume the mean vector tjIt itself subject to estimation errors and, given all publicly available
information, is distributed as
tjIt
N(b
t; b
t); (28)
25The issue not addressed in the Black-Litterman model is the statistical computations to infer the covariances,
which is a vast subject studied by both academics and practitioners.
26The risk-free rate is the rate of return of so-called risk-free securities in the sense that they are supposed to
oer a sure rate of returns. Most of bonds are not risk-free as the issuer can default (even countries). For example,
only treasury bills from the U.S. government (and a few other) is considered as risk-free.

176. The Black-Litterman model and extensions 25
where we also assume that the estimation error's covariance on tjIt is proportional to the
estimated covariance (if is equal to zero, there is no estimation error) and b
t is a prior to be
estimated.
3.2 Second pillar: CAPM reverse optimization
The second pillar of the Black-Litterman model lies in the de

177. nition of this prior. It starts with
the observation that the mean-variance allocation suers from over-sensitivity to the vector of
expected returns. In [9], it is shown for instance that a small shift in the expected return of
a single asset can yield an entirely dierent portfolio. Furthermore, the historical estimator27
is known to lead to counter-intuitive portfolios, as we show in the following example with the
20 largest stocks (in term of market capitalization) from the universe we presented in the

178. rst
chapter. Taking two years of weekly returns (from December 23 2009 till December 28 2011),
1.5 2.5 3.5 4.5
0.0 0.5 1.0 1.5 2.0
Volatility (%)
Expected return (%)
1.5 2.5 3.5 4.5
−1000 −500 0 500 1000
Weight in portfolio (%)
Volatility (%)
Unconstrained
1.5 2.5 3.5 4.5
0.0 0.5 1.0 1.5 2.0
Volatility (%)
Expected return (%)
1.5 2.5 3.5 4.5
0 20 40 60 80 100
Weight in portfolio (%)
Volatility (%)
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ORCL
MSFT
KO
XOM
GE
IBM
PEP
AAPL
PG
ABT
PFE
JNJ
OXY
WFC
MCD
WMT
INTC
CSCO
QCOM
AMZN
Long−only
Figure 6: Mean-variance allocation using the historical estimator. On the left-hand side, the triangles
represent the individual security expected returns and volatilities. In blue and green, we showed the two
securities with maximal expected returns.
we show the results of a mean-variance optimization both in the unconstrained (except for the
27b
t =
PT
k=0 (r1;tk rf;tk) =(T + 1); ;
PT
k=0 (rn;tk rf;tk) =(T + 1)

179. 26 Views Integration in Quantitative Portfolio Allocation
budget constraint) and long-only constrained (with wi 0 for all i) cases in

180. gure 6. In the

181. rst case, the optimizer returns very large long and short positions, whereas the long-only
optimizer returns positions concentrated on a very small number of assets (those of maximal
expected return).
Moreover, this historical estimator is only one investor's personal perspective. When Black and
Litterman developed their work, the semi-ecient form of EMH was not as disputed as it is today.
This is why they based their prior on the hypothesis that the market for liquid stocks and bonds
showed semi-eciency. In short, they supposed that any rational investor should in principle
know that the market cannot be beaten without access to private information, and therefore
should hold a combination of the market portfolio and a risk-free asset in order to achieve any
level of risk desired28. Knowing this, the idea of a portfolio optimization who would not take the
market expectation into account is pointless. Furthermore, any consistent optimization with a
risk aversion equal to that of the market should yield the market portfolio. In fact, the Black-
Litterman method consists in a way for investors to tilt the market portfolio with respect to their
private information. Based on these considerations, the Black-Litterman model uses the CAPM
to construct an economically motivated prior. Basically, under some equilibrium assumptions,
the CAPM states that any security's expected return over the risk free rate should be equal to
that of the expected market excess return times its (linear) exposure to the market excess return,
that is
b
t =b

182. t
bE
(rm;t+1) rf;t
+ rf;t; (29)
with bE
(rm;t+1) the expected return of the market for the next period and rf;t the risk-free rate
at time t. b

183. t is the vector of market exposures, which can be either obtained as implied betas
b

184. i;t = b
twm;t=b2
m;t
29 or with an OLS regression on the sample period de

185. ning regression-based
betas b

186. r;t
30. In [34], Idzorek shows that the range and standard deviation of b
t is much smaller
than that of b
t with both types of betas. This re-centering of the most extreme values is linked
to the Bayesian concept of shrinkage estimation and we give a working example later in the
next subsection when implementing actual market views. To continue our example, we de

187. ne
the market weights as a capitalization-weighted benchmark of our 20-stock universe, and set the
risk-free rate at 0. In

188. gure 7, we show the Black Litterman's reverse optimization (assuming
= 0 for simplicity), that is the mean-variance optimized portfolios obtained using the CAPM
28To obtain an expected return larger than the market, one needs to short the risk-free asset in order to buy
more of the market portfolio, inducing leverage and also a larger risk.
29For example if the whole market is investible and its weights accessible, that is if one can use the market as
the universe's benchmark.
30We stress the fact that b

189. r;t6= b

190. i;t in general, as it is shown in [33]

191. The Black-Litterman model and extensions 27
prior instead of the historical estimator, both in the unconstrained and long-only cases. The two
dashed black lines show the market Sharpe ratio bE
(rm;t+1) =bm;t, that is the market expected
bE
return per unit of risk, which is the highest on the ecient frontier in the CAPM. One may
notice it was not the case when using the historical estimator, where Sharpe ratios four times
larger were found (inconsistently with the CAPM). The two vertical black lines are the portfolios
obtained by using a risk-aversion equal to the market Sharpe ratio divided by its volatility, that
is
= (rm;t+1) =b2
m;t, and we observe that both solutions are in fact the market portfolio
w
;t = wm;t. An intuitive explanation can also be given in terms of the unconstrained solution
1.5 2.5 3.5 4.5
0.15 0.25 0.35
Volatility (%)
Expected return (%)
1.5 2.5 3.5 4.5
−200 0 100 200
Weight in portfolio (%)
Volatility (%)
Unconstrained
1.5 2.5 3.5 4.5
0.15 0.25 0.35
Volatility (%)
Expected return (%)
1.5 2.5 3.5 4.5 0 20 40 60 80 100
Weight in portfolio (%) Volatility (%)
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ORCL
MSFT
KO
XOM
GE
IBM
PEP
AAPL
PG
ABT
PFE
JNJ
OXY
WFC
MCD
WMT
INTC
CSCO
QCOM
AMZN
Long−only
Figure 7: Mean-variance allocation using the CAPM prior.
of the mean-variance optimization. Let us write the weights that maximize the Markowitz's
expected utility criterion (equation (7)), but without requiring them to sum up to one in the
Lagrangian of equation (9), which gives a dierent solution than equation (10), that is
w
p;t =
b
1
t
b
t =
b
1
t
b

192. t
bE
(rm;t+1)
=
bE
(rm;t+1)wm;t
b2
m;t
: (30)
By inspecting this equation, one observes that the budget and long-only constraints are satis

193. ed

194. 28 Views Integration in Quantitative Portfolio Allocation
for the risk-aversion described above, and as the unconstrained minimization returns the market
portfolio, adding a budget or a long-only constraint does not change the result of the optimization
at this point.
3.3 Third pillar: Bayesian views integration
The third pillar of the Black-Litterman model lies in the integration of market views using
Bayes rule and the reference model. In fact, even if the CAPM may seem old-fashioned, any
(equilibrium or not) prior can be used and the results implied by considering only the

195. rst and
third pillars remain applicable with b
t or any estimate of future returns. The view framework
at time t extending public information It to private information Jt consists of three distinct
elements.
The focus selects linear combinations of the risk-factors on which one has views: a K n
pick matrix bQ
t
31. Thus, one can input views on separate factors or on portfolios of
factors.
The views is a K 1 vector of random variables qtjIt;Jt = (q1; ; qK) embedding the
expectations of the focus. It is a vector that the user will need to estimate by assigning
values corresponding to his views.
The con

196. dences represent view-estimation errors: a K K matrix b
t
32 which is often
chosen to be diagonal for simplicity, meaning that the con

197. dences in the dierent views
are uncorrelated.
bQ
t =
0
BB@
bQ
1;1 bQ1;n
...
. . .
...
bQ
K;1 bQ
K;n
1
CCA
and b
t =
0
BB@
b
1;1 0
...
. . .
...
0 b
K;K
1
CCA
(31)
For tjIt;Jt
d
6=tjIt
33, it is assumed that
bQ
ttjIt;Jt = qtjIt;Jt + tjIt;Jt ; (32)
31The hat expresses the fact that the user has to choose a focus which determines a known view structure: this
matrix is not random).
32The hat expresses the fact that the user inputs con

198. dence in his views by himself: this matrix is not random.
33We stress that in the original formulation of the model, the views are expressed on the market estimates rather
than on the market itself. This has important consequences that we outline below.

199. The Black-Litterman model and extensions 29
where tjIt;Jt N(0;b
t) and 0 is a vector of zeros. Therefore, conditionally on tjIt;Jt , we can
write qtjt;It;Jt
N(bQ
ttjIt;Jt ;b
t). Supposing now that our best estimate of qtjt;It;Jt is bqt (i.e.
our view), it is possible to obtain analytical expressions for the parameters of the distribution of
tjIt;Jt conditional on the views bqt using Bayes rule and write
tjIt;Jt
N(e
t;e
t); (33)
where
e
t
b
t
1
+ bQ
t
b
1
t
bQ
t
1
and e
t e
t
b
t
1
b
t + bQ
t
b
1
t bqt
. (34)
The full proof can be found for example in [48, 34, 17]. We note that, as expected, when the
user does not input any view (bQ
t = b
t = bqt = 0), e
t = b
t, e
t = b
t and thus tjIt;Jt
d=
tjIt(or
equivalently E[rt+1jIt;Jt] E[rt+1jIt]). Moreover, the intuition behind the con

200. dence is the
following: suppose one only wants to input a view bq1;t on a single security i (i.e. the matrix
bQ
t picks one security). If
1;1jIt;Jt goes to in

201. nity, then we also have e
t = b
t, e
t = b
t and
thus tjbq
t
d=
t. However, as
1;1jIt;Jt goes to zero, there is no view estimation error (i.e. full
con

202. dence) and we have ei;t = bq1;t, that is the view replaces the original forecast for this security.
As the whole distribution of risk-factors is determined by the

203. rst two moments in normal
markets, this method represents an elegant way of modifying the input of a traditional mean-variance
optimizer. To be fully consistent, we should then write the new posterior market
model xt+1jIt;Jt N(e
t;b
t + e
t). Thus, we observe that the no view posterior xt+1jIt
N(b
t; (1 + )b
t) is dierent from the reference model xt+1jIt N(b
t;b
t) one could expect:
e
because of the estimation e
e
e
error, the variance has increased. Setting = 0 (meaning that the
uncertainty in the mean is negligible compared to that of the returns as in [10]) yields the reference
model and the market portfolio with
as before. An alternative market based formulation
allows one to input views directly on the market rather than on its distribution's

204. rst moment
estimates is proposed in [48]. An appealing feature of this formulation is that the parameter
is eliminated, implying xt+1jIt;Jt N(t;t) with t and t slightly dierent from equation
(34), as we have
e
t b
t b
tbQ
t
h
bQ
t
b
tbQ
t + b
t
i1 bQ
t
b
t
and e
t b
t + b
tbQ
t
h
bQ
t
b
tbQ
t + b
t
i1 h
bqt bQ
tb
t
i
. (35)
For a discussion of the parameter in the Black-Litterman model, and in particular its link to
uncertainty and estimation error, we refer to [60]. It should

205. nally be noted that the market

206. 30 Views Integration in Quantitative Portfolio Allocation
bE
formulation was extended to the larger family of elliptical distributions34 for the reference model
in [61], thus making the Black Litterman market model and views integration framework useful
for a wider class of asset allocation schemes. Another possibility adopted for example in [17] is
to simply use the distribution of the mean vector instead of the market (xt+1jIt;Jt ! tjIt;Jt)
for the optimization. This last possibility has the advantage of simplicity, as it tilts directly the
reverse optimized market portfolio. To emphasize this interpretation, we consider the market's
implied risk-aversion
= (rm;t+1) =b2
m;t and write the updated (completely) unconstrained
weights, tilted from equation (30) to
w
p;t =
e
1
t
e
t =
e
1
t
e
t
b
t
1
b
t + bQ
t
b
1
t bqt
=
1
wm;t + bQ
t
b
t
1
bqt
; (36)
where the last equality comes from replacing b
t by its expression from equation (29). Setting
= 1 (meaning that the uncertainty in the mean is equal to that of the returns), we observe
that the

207. rst term is the market portfolio, whereas the second term consists of deviations from
this portfolio.
To continue our example, we use this last approach and consider that a year counts 50 trading
weeks to discuss the results in terms of annualized returns. In the two columns of table 2, we
present the annualized expected returns for the historical and CAPM's expected returns. As in
[34], we observe that the range (dierence between max and min) for the CAPM's implied returns
is smaller, as both extremes are shrinked toward the capitalization-weighted mean. As we used
implied betas, the weighted mean does indeed not change. We represent now the health sector as
a capitalization-weighted benchmark of the 3 healths stocks present in the sample according to
their Standard Industrial Classi

208. cation (or SIC codes), that is ABT, PFE and JNJ. The expected
return of this portfolio is 10:9%. Let us implement two dierent views with dierent degrees of
con

209. dence. The

210. rst view is bearish on the market and we decrease its expected return from
14:8% to 13%. The second view is bullish on the health sector and we increase its expected
return from 10:9% to 13%. To implement the views, the pick-matrix is a 2 20 matrix with
the market weights wm;t on the

211. rst row and the market weights of the health stocks divided by
d=
34To de

212. ne elliptical distributions formally, one

213. rst need to de

214. ne spherical distributions. A d 1 random
vector x = (x1; ; xd) has a spherical distribution if Ux x for every U 2 dd R
such that UU= UU = Id,
d=
with Id the d d identity. The uncorrelated standard normal N (0; Id), with 0 a d 1 vector of zeros, is an
example of spherical distribution. Then a d 1 random vector y = (y1; ; yd) has an elliptical distribution if
y +Cx, with a scalar vector 2 dR
, a scalar matrix C 2 dd R
and x has a spherical distribution.

215. The Black-Litterman model and extensions 31
their sum on the second row. To see the eect of the views, we de

216. ne
b
1 =
104 0
0 106
!
and b
2 =
106 0
0 103
!
:
Initial CAPM View 1 View 2
ORCL 9.5 19.12 17.03 19.86
MSFT -2.43 17.15 15.3 17.76
KO 12.98 10.42 9.32 10.87
XOM 15.5 15.99 14.27 16.64
GE 14.16 22.39 19.92 23.3
IBM 22.65 14.48 12.92 15.01
PEP 8.35 10.41 9.31 10.86
AAPL 45 16.89 15.06 17.44
PG 7.38 7.53 6.75 7.79
ABT 6.31 9.59 8.58 10.11
PFE 14.45 13.23 11.82 14.09
JNJ 4.99 9.5 8.5 10.04
OXY 14.75 19.55 17.41 20.36
WFC 8.69 24.04 21.37 24.97
MCD 29.41 6.75 6.05 7.03
WMT 9.18 8 7.17 8.33
INTC 18.57 18.76 16.71 19.42
CSCO -6.15 20.92 18.62 21.75
QCOM 16.09 17.68 15.76 18.34
AMZN 22.06 17.99 16.03 18.6
Min -6.15 6.75 6.05 7.03
Max 45 24.04 21.37 24.97
Mean 14.89 14.89 13.29 15.48
Table 2: Expected return estimates.
In the two last columns of table 2, we present
the annualized expected returns for the two
views. In the

217. rst case, we observe than all
values and thus both the min, the max and
the mean are lower as expected. In the sec-ond
case, we also observe that the health sec-tor's
stocks have a greater return as expected,
but that all other stocks follow. This can be
explained by the large average correlation of
0:525 between the weekly returns in this sam-ple:
a bullish view on a few stocks tends to pull
up all the others. Furthermore, as the con

218. -
dence in the

219. rst view is larger, we observe in
the table that the expected return in the

220. rst
case is quite close to the view. However, as
the con

221. dence in the second view is an order
of magnitude lower, the tilt toward the view
is less eective and the expected return (fore-cast)
of the health sector in this case is only
11:6%.
In

222. gure 8, we show portfolios optimized with
the original market risk aversion along with
the market portfolio. As the expected returns
and covariance matrix have been updated by
the views, we observe that the optimizer re-turns
fairly dierent portfolios. In the

223. rst
case, tilts are obtained by selling short (or in the long-only case by simply not allocating) the
securities with smaller expected return, to buy more of the others. This can be explained by
the original market risk-aversion of 5:04 that we fed in the optimizer which is bullish in our new

224. 32 Views Integration in Quantitative Portfolio Allocation
Figure 8: Market (in blue), unconstrained (in red) and constrained (in green) optimal portfolios.
market, whose implied risk-aversion (i.e. the new market risk-aversion de

225. ned with updated
expected returns and covariance matrix) is 7:48. In the second case, the new market implied risk
aversion is 6:61, so the original risk-aversion of 5:04 is small again and we adjust the portfolio
positions mostly by buying more of the health stocks. It should be noted that in the constrained
case, one would not hold ABT even though he is one of the three health stocks. It can be ex-plained
by the fact that its updated expected return is one of the smallest among the considered
stocks, even with the bullish view.
The literature on the Black-Litterman model is rich and many extensions can be found. In the
next subsection, we describe one of particular relevance in the context, as it extends the model
to views on exogenous factors, while keeping everything else unchanged. Furthermore, given the
similarity between the new results and the original model, many extensions developed in the
literature (such as the market formulation for elliptical distributions) could then also be applied
to the Augmented Black-Litterman model [20, 18, 19].
3.4 The Augmented Black-Litterman model
Given the popularity of factor models to construct portfolios, the possibility of inputting views
on exogenous risk-factors such as fundamental (e.g. the Fama-French factors), technical (e.g.
momentum eects35) or macro-economic (e.g. oil prices for airlines, or FX rates for exporting

226. rms or measures) proved to be of utmost importance in practical applications. In line with this
observation, Cheung proposes an Augmented Black-Litterman model in [20, 18, 19] where he
elegantly extends the original Black-Litterman model to linear factor models while keeping the
35The eect can be summarized by winner stocks keeps winning and looser stocks keeps loosing.

227. The Black-Litterman model and extensions 33
Gaussian assumption, a market equilibrium prior, and Bayesian update to obtain the posterior
distribution. Starting from the linear factor model described by equation (20), we use the n 1
vector of factors xt of security returns and the L1 vector of factors yt, as well as a the intercept
and B the matrix of exposures. Then we de

228. ne the (2n + L) 1 augmented view universe vt
and the (n + L) 1 analytical view universe at
36 as
vt =
0
B@
xt
yt
t
1
CA
and at =
xt
yt
!
: (37)
The view universe corresponds to the three parts (the securities themselves, the factors, and
the residuals, that is the idiosyncratic returns) on which an investor can input views, whereas
the analytical universe is the one on which the (Bayesian) analysis is based. Following what we
emphasized at the end of the preceding subsection, we work on the distribution of the vector of
expectations instead of the distribution of the analytical universe, that is
at+1jIt N(a tjIt ;b
a
t ) ! a tjIt
N(b
at
; b
a
t ); (38)
where
b
at
=
0
BBB@
b
xt
|{z}
n1
y
|{zt}
L1
b
1
CCCA
=
0
BBB@
b
y
|{zt}
nn
b
y
t B
| {z }
Ln
1
CCCA
|w{mz;}t
n1
and b
a
t =
0
BBB@
b
x
|{zt}
nn
Bb
y
| {z t}
nL
b
y
t B
| {z }
Ln
b
y
|{zt}
LL
1
CCCA
; (39)
with
= bE
m;t is the market implied Sharpe ratio divided by its volatility, b
(rm;t+1) =b2
x
t =
Bb
y
t B + b
t , coming from the assumption of residuals uncorrelated to factors (which is the
case if the exposure matrix is estimated via an OLS), b
y
t and b
t the covariance matrix estimators
for the factors and the residuals. As with Black-Litterman, we can use CAPM prior estimates,
but the results we present in what follows also hold for any prior estimates. Again, the framework
extending the public information It to include private information Jt consists of three distinct
elements.
The focus selects K1 securities, K2 factors and K3 idiosyncratic returns on which one has
views. With K = K1 + K2 + K3, it represents a K (2n + L) augmented pick matrix
bQ
v
t . In Cheung's approach, bQ
v
t is supposed to be block-diagonal with blocks of size K1n,
K2 L and K3 n: this means that one can input views on linear combinations of the
36The terms augmented view universe and analytical view universe are borrowed from Cheung.

229. 34 Views Integration in Quantitative Portfolio Allocation
securities (i.e. portfolios), factors, or idiosyncratic returns, but for simplicity no cross-type
is admitted (i.e. views mixing the three types).
The views is a K 1 vector of random variables qv tjIt;Jt
, de

230. ned as qtjIt;Jt in the original
Black-Litterman approach (i.e. embedding the expectations of the focus) but with three
distinct parts.
The con

231. dences represent augmented view-estimation errors: a K K block diagonal
(because of the no cross-type view restriction) matrix b
t
37.
qv tjIt;Jt =
0
BB@
qx tjIt;Jt
qy
tjIt;Jt
q tjIt;Jt
1
CCA
, bQ
v
t =
0
BBBBBBBB@
bQ
x
|{zt}
K1n
0
...
bQ
y
|{zt}
K2L
...
0 bQ
|{zt}
K3n
1
CCCCCCCCA
, b
t =
0
BBBBBBBB@
b
x
|{zt}
K1n
0
...
b
y
|{zt}
K2L
...
0 b
|{zt}
K3n
1
CCCCCCCCA
(40)
For the new random variable v tjIt;Jt
=
E[xt+1jIt;Jt] ; E
yt+1jIt;Jt
; E[t+1jIt;Jt]
,
it is assumed that
bQ
v
tv tjIt;Jt = qv tjIt;Jt + v tjIt;Jt ; (41)
where v tjIt;Jt
N(0;b
t). Equivalently, it it possible to write equation (41) directly on the
analytical universe as
bQ
a
t a tjIt;Jt = qa tjIt;Jt + a tjIt;Jt ; (42)
with qa tjIt;Jt
= qv tjIt;Jt
+bc
t
38 and
a tjIt;Jt =
E[xt+1jIt;Jt]
E
yt+1jIt;Jt
!
, bQ
a
t =
0
BBBBBBBB@
bQ
x
|{zt}
K1n
|{0z}
K1L
|{0z}
K2n
bQ
y
|{zt}
K2L
|{0z}
K3n
bQ
tB | {z }
K3L
1
CCCCCCCCA
andbc
t =
0
BBBBBBB@
|{0z}
K11
|{0z}
K21
bQ
t a |{z}
K31
1
CCCCCCCA
. (43)
37In fact, as in the original Black-Litterman model, the blocks themselves are often chosen diagonal for the user's
convenience, meaning that the con

232. dences in the dierent views are uncorrelated.
38Here we assume that the vector a coming from equation (20) is known for sure, that is we leave aside the
error coming from the estimation of the factor model.

233. The Black-Litterman model and extensions 35
Therefore, conditional on a tjIt;Jt
, we can write qa tjat
;It;Jt
N(bQ
a
t a tjIt;Jt
a
t ) = N(bQ
;b
v
tv tjIt;Jt
+
t;b
t). Supposing now our best estimate of qv tjvt
bc
;It;Jt
is bqvt
, then that of qa tjat
;It;Jt
is bqvt
+bc
t.
Thus, it is possible to obtain an analytical formula similar to the original Black-Litterman in
equation (38), that is
a tjIt;Jt
N(e
at
;e
a
t ); (44)
where
e
a
t
b
a
t
1
+
bQ
a
t
b
a
t
1 bQ
a
t
1
and e
at
e
a
t
b
a
t
1
b
at
+
bQ
a
t
b
a
t
1
(bqvt
+bc
: (45)
t)
bE
The proof, which relies on that of the Black-Litterman model, can be found in [20]. As for
the original Black-Litterman model, an interesting intuition can be obtained by considering the
(completely) unconstrained solution of the mean-variance equation using the market implied
risk-aversion
= (rm;t+1) =b2
m;t. In this case, we can write the updated unconstrained weights
with positions modi

234. ed from the solution presented in equation (30) to
w
p;t =
1
wm;t +
bQ
x
t
b
x
t
1
bqxt
+ cM
bQ
y
t
b
y
t
1
bqy
t +
1 BcM
bQ
t
b
t
1
bqt
; (46)
where we de

235. ne
cM
=
e
x
t
1
Be
y
t
; (47)
e
x
t = Be
y
t B + e
t ;
e
y
t =
b
y
t
1
+
bQ
y
t
b
y
t
1 bQ
y
t
1
;
and e
t =
b
t
1
+
bQ
t
b
t
1 bQ
t
1
:
In equation (47), the interpretation of the parameters is straightforward: e
x
t is the covariance
matrix of securities updated by factor and idiosyncratic views only, e
y
t is the covariance matrix
of factors updated by factor views only and e
y
t is the covariance matrix of idiosyncratic returns
updated by idiosyncratic views only. Going back to the right-hand side of equation (46), we
can interpret the two

236. rst terms exactly as in the original BL model, while the third and fourth

237. 36 Views Integration in Quantitative Portfolio Allocation
terms represent tilts induced by factor and idiosyncratic views. The proof of this transparent
allocation using the Augmented Black-Litterman model can be found in [18].
We have seen that the Black-Litterman model and its extensions provide a uni

238. ed Bayesian
allocation framework. First, it addresses a major issue of the mean-variance allocation by using
a concept of market equilibrium for the prior view. Second, it gives the possibility to input views
on expected returns in a mathematically sound way. Finally, an augmented extension exists, that
provides investors with endogenous techniques to combine strategies, mimic exogenous factors
or make stock-speci

239. c bets. However, it is well known that the distribution of returns for most

240. nancial assets exhibits excess kurtosis and negative skewness, and thus the Gaussian hypothesis
is most often rejected. Furthermore, a la Black-Litterman models (and extensions to elliptical
distributions as in [61]) based on Gaussian distributions do not allow the user to input views on
anything else than the

241. rst moment of the return distribution, which has limited applications. In
practice, one may want to express a view on many other features of the distribution, as discussed
in 2.2. In what follows, we describe how this can be achieved using Monte-Carlo simulations and
a scenario-based approach.
4 The scenario-based approach
When leaving the Gaussian world and its handy analytical formulas, we open ourselves to
scenario-based methods. Within this new framework, it becomes possible to input non-linear
views on non-linear focuses and in non-Gaussian markets. In this chapter, we present one of
the alternative approaches, namely the Entropy Pooling, with completely dierent theoretical
grounds39. InFully
exible views: theory and practicepublished in 2008, Meucci suggests to use
an information theoretic concept for inference. The central idea is that the posterior distribution
e Fxt+1jIt;Jt incorporating private information should at the same time satisfy the market views
and be as close as possible to the prior distribution Fxt+1jIt inferred from the publicly available in-formation.
It is based on the idea of minimizing informational discrepancy between distributions
through relative entropy minimization, which is a widely studied subject and

242. nds applications
in various

243. elds of science and engineering [40]. In

244. nance, it is mainly used for option pricing
in [15, 4, 3] and views integration in [47, 51, 49, 52]. As changing of probability measure (from
the real-world to the risk-neutral in option pricing or view-based in portfolio allocation) is
the central concept in both applications, they need as input enough scenarios for the risk-factors
to approximate and calibrate continuous distribution of interest. In portfolio allocation, when
39It should also be noted that a scenario-based extension of the Bayesian framework is also proposed in [16],
using the concept of importance sampling.

245. The scenario-based approach 37
one thinks about newly-issued securities or especially if one considers re-balancing at a weekly
or monthly frequency, the required scenarios cannot be found in historical data. Moreover, it
may not always be wise to use data from a much distant past40. Thus, one often needs a market
model to generate the required scenarios, hence the one we also present and use in this chapter.
4.1 Learning from disorder
We start by considering a discrete random variable x with possible outcomes
x = fx1; ; xng.
For p a discrete probability distribution41 on
x, Shannon's entropy S (p) is de

246. ned as
S (p) =
Xn
i=1
p (xi) log p (xi) : (48)
Furthermore, considering a new probability distribution ep6= p, the relative entropy D(ep; p) is
de

247. ned as
D(ep; p) =
Xn
i=1
ep (xi) log
ep (xi)
p (xi)
: (49)
While the

248. rst is a measure of the uncertainty contained in a probability distribution, reaching
its maximum if no outcome is more likely than another, the latter is an asymmetric measure of
distortion between probability distributions, reaching its minimum when the distributions are
equivalent.
We can give an intuition using a classical example: let us consider a coin c with two possible
outcomes, that is
c = fh; tg with h for heads and t for tails and p(h) = 1 p(t). Sup-pose
moreover that the coin is biased towards heads, that is p(h) 0:5 p(t). If we
ip
it, there is less uncertainty about the outcome than if the coin was fair, hence a smaller en-tropy.
This is illustrated by the black curve in

249. gure 9, where p(h) is represented on the
horizontal axis and the entropy S(p) =
P
ci2fh;tg p (ci) log p (ci) on the vertical axis. We ob-serve
that the maximal biases with lim p(h) ! f0; 1g (i.e. no uncertainty about the outcome)
yield the two entropic minimas. Conversely, the fair coin with p(h) = 1=2 (i.e. maximal un-certainty
about the outcome) corresponds to maximal P
entropy and it is straightforward to un-derstand
that the relative entropy D(ep; p) =
ci2fh;tg ep (ci) log 2ep (ci) between a biased coin
40Does the market really show the same characteristics today as it did twenty years ago?
41We de

250. ne p Pon
x with p(xi) being the probability associated with the event xi, that is p(xi) 0 8i 2
f1; ; ng and
n
i=1 p(xi) = 1.

251. 38 Views Integration in Quantitative Portfolio Allocation
(with ep(h) 2 ]0; 1[) and a fair coin mirrors the entropy with a downward shift by log 2, rep-resented
by the blue curve in

252. gure 9. Furthermore, we show with the red curve in

253. gure
9 (the relative entropy D(p; ep) between a fair coin and a biased coin), that this quantity is
not symmetric as previously emphasized. Finally, we observe that both D(ep; p) and D(p; ep)
are either concave or convex (and zero for ep p), an important property we will use later.
0.0 0.2 0.4 0.6 0.8 1.0
−4 −3 −2 −1 0
Figure 9: Coin
ip's entropy S (p) (black) and rel-
ative entropies D(ep; p) (blue) and D(p; ep) (red)
Let us go back to the continuous case with the
risk-factor distribution Fxt+1jFt . From now on,
and until we present our market model in sub-section
4.5, we drop index t to avoid cumber-some
notations. The distribution of possible
outcomes over the next investment period is
denoted FxjF instead of Fxt+1jFt . We denote
P
x;F the set of all probability measures on
(
x;F) and have FxjI 2 P
x;F for I F,
that is the probability measure inferred from
publicly available information is included in
the set of all probability measures on the mar-ket.
We use P
x;F
FxjI
to denote the set
of probability measures absolutely continuous
with respect to the probability
measure FxjI ,
that is F e 2 P
x;F
FxjI
if for all subsets
x such that FxjI
= 0 implies e F
= 0. For all e F 2 P
x;F
FxjI
, if log
d e F
dFxjI
is
integrable, the Kullback-Leibler's divergence, or relative entropy, is de

254. ned as
DKL
e F; FxjI
=
x
log
d e F
dFxjI
!
d e F;
=
x
log
e f (x)
fxjI (x)
!
e f (x) dx; (50)
where d e F
dFxjI
is the Radon-Nikodym density of e F with respect to FxjI . In the second equality, we
simply rewrote the expression in terms of the probability densities.
The Kullback Leibler's divergence is a member of the f-divergences (Csiszar [22] and Ali
Silvey
[2]), a family of distortion measures between probability distributions. For all F e 2 P
x;F
FxjI
,
members of this family are characterized by a convex generator function f : ! R on domf =

255. The scenario-based approach 39
R, such that f (1) = 0 and the f-divergence equals
Df
e F; FxjI
=
x
f
d e F
dFxjI
!
dFxjI
=
x
f
e f (x)
fxjI (x)
!
f (x) dx: (51)
In the table below, we present two generator functions and their associated divergences:
Symb Name f(t) Divergence
DKL Kullback-Leibler tlog t (t 1)
x
h
log
d e F
dFxjI
d e F + dFxjI d e F
i
DJS Jensen-Shannon tlog
2t
t+1
log
t+1
2
DKL
e F;
FxjI+ e F
2
+DKL
FxjI ;
FxjI+ e F
2
Table 3: Entropy based f-divergences: it should be noted that we present here a slightly modi

256. ed version
of the Jensen-Shannon divergence, that is 2DJS, and we give the reason for this choice in subsection 4.4.
As explained in the introduction of this chapter, Meucci's idea is to de

257. ne the posterior distri-bution
e FxjI;J by incorporating private information and being as close as possible to the prior
distribution FxjI inferred from the publicly available information (in terms of informational dis-crepancy).
In [47], Meucci suggests a procedure that is called entropy pooling, in order to
de

258. ne
e FxjI;J argmin
e F2V
DKL
e F; FxjI
; (52)
where e F 2 V P
x;F
FxjI
stands for all the distributions which satisfy the views and are at
the same time absolutely
continuous
with respect to FxjI . With our formalism, the null view
J I implies V = P
x;F
FxjI
, or equivalently FxjI;J e t FxjI . Within this framework, views
are formulated as a set of K1 equality and K2 inequality constraints
e F 2 V ()
8 :
e F 2 P
x;F
FxjI
;
x
Hid e F =
x
Hi (x) e f (x) dx = hi 8i = 1; ;K1;
x
Gjd e F =
x
Gi (x) e f (x) dx gj 8j = 1; ;K2:
(53)
For example, let us come back to the investor forecasting a large positive jump in the price of
stock i over the next investment period, who expressed his belief on the expected return of stock
i as eE
[rijI;J ] = hi (i.e. a constraint on the

259. rst moment of the distribution). The posterior
e FxjI;J 2 P
x;F
FxjI
is then chosen such that

260. 40 Views Integration in Quantitative Portfolio Allocation
it minimizes the Kullback-Leibler's divergence, that is the distortion with respect to the
probability measure inferred from the publicly available information, and
it incorporates private information, that is
x
xi e f (x) dx =
xi
xi e fi (xi) dxi = hi with
xi ri.
If the investor's belief is formulated as an interval with lower and upper bounds li and ui, he
can simply specify li
xi
xi e fi (xi) dxi ui. Furthermore, Meucci suggests a way to input
con

261. dence exogenously in this model by considering a shrinkage between the prior and posterior
densities as
e fxjc;I;J = (1 c) fxjI + c e fxjI;J ;
where c 2 [0; 1] represents the con

262. dence in the views. This shrinkage a posteriori is called
opinion pooling and can be used for example to pool the opinions of dierent managers. It has
deep implications and is very dierent from the endogenous way of inputing con

263. dence in the
Black-Litterman model, as we show in the next subsection with an analytical example where the
entropy pooling is applied to Gaussian markets and views a la Black-Litterman.
4.2 Analytical example
It starts by considering the n risk-factors distributed as a multivariate normal as in Black-
Litterman, that is we assume our prior to be
xjI N (;) : (54)
Suppose one wants to express K1 views as in Black-Litterman with a K1 n pick-matrix Q and
the K1 1 vector of expectations e
Q for the K1 1 focus QxjI;J , but also K2 views on the
variances/covariances with a K2 n pick-matrix G and the K2 K2 covariance matrix e
G for
the K21 focus GxjI;J . Following the precedent subsection, the posterior distribution e F, whose
density can be written e f (x) = 1
n=2dete
(2)
exp
h
1
2 (x e) e
1
(x e)
i
, should satisfy
e F 2 V ()
8
:
x
(Gx)i
e f (x) dx = G;i; 8i = 1; ;K2;
x
(Gx)i (Gx)j
e f (x) dx = 2G
;i;j 8i = 1; ;K2 and 8j = i; ;K2;
x
(Qx)i
e f (x) dx =
e
Q
i
8i = 1; ;K1;
2G
;i;j G;iG;j =
e
G
i;j
8i = 1; ;K2 and 8j = i; ;K2:
(55)

264. The scenario-based approach 41
For two multivariate normal distributions N (;) and N
e
of dimension n, the Kullback-
;e
Leibler's divergence reads
DKL
e F; F
=
1
2
tr
1e
+ ( e) 1 ( e) log
dete
det
!
n
!
; (56)
where tr and det represent respectively the trace and the determinant of a matrix. Taking the
minimum of this expression under the constraints given in equation (55) yields the posterior
distribution
xjI;J N
; (57)
e;e
where
e
+ G
h
Me
GM M
i
G and e
+ Q
QQ
1
e
; (58)
Q Q
with M =
GG1
. The full proof can be found in [47]. We consider two assets to give an
intuition on this model and show the dierence with the Black-Litterman formula. We represent
these assets with a 2 1 random vector x = (x1; x2) with x1 N(0; 1), x2 N(0; 1) and
Cov (x1; x2) = 0:6, and show the prior (standard normal) marginals as the black curves of

265. gure 10. Then we input the two following views:
−4 −2 0 2 4
0.0 0.1 0.2 0.3 0.4 0.5 0.6
x1
Density
−4 −2 0 2 4
0.0 0.1 0.2 0.3 0.4 0.5 0.6
x2
Density
Figure 10: First asset on the left and second on the right with prior (black) distribution, full-con

266. dence
(blue) and half-con

267. dence (red) updated posterior distributions for the analytical entropy pooling.
Q = (1; 0) with e
Q = 0:5, that is we increase the expected value of the

268. rst asset to 0:5.
G = (1; 0) with e
G = 0:92, that is we decrease the volatility of the

269. rst asset to 0:9.

270. 42 Views Integration in Quantitative Portfolio Allocation
We show the updated marginals (blue curves) in

271. gure 10 and observe that the expected value
of the second asset has decreased to 0:3 as both assets were originally anti-correlated. To show
the eect of the con

272. dence, we represent the half-con

273. dence (c = 0:5) marginals with red curves
in

274. gure 10, and observe the shrinkage of the prior towards the view. It is interesting to compare
this formula with the market formulation of BL, considering the same focus for expectations and
covariances, that is G Q, and e
G 0 with 0 the K1 K1 matrix of zeros. Doing this, the
full-con

275. dence updated expectations and covariances in equation (58) are the same as those of
equation (35), without view estimation error (i.e. b
t 0).
−4 −2 0 2 4 6
0.0 0.2 0.4 0.6 0.8
x1
Density
Prior
View
EP posterior
BL posterior
Figure 11: Dierence between Bayesian blend-
ing and opinion pooling.
There is nonetheless a fundamental dierence be-tween
the Bayesian view blending and the entropy
pooling, which lies in the con

276. dence input. We
illustrate this with an extreme view on the ex-pectation
of the

277. rst asset, for instance e
Q = 3,
and use the original Black-Litterman updated pos-teriors
from equation (34) with = 1, that is the
formulas we used in the example of subsection 3.1.
If we set b
t 1 and c = 0:5, we have the same
updated expectations for the

278. rst asset, that is
e1 = e1 = 1:5. However, as shown in

279. gure 11,
the two resulting distributions are signi

280. cantly dif-ferent,
and this divergence increases with the dif-ference
between prior and view.
4.3 Fully flexible probabilities
As discussed in the introduction of the chapter, our goal here is to input views on non-linear
combinations of non-Gaussian risk-factors. This is why Meucci proposes in [47] a non-parametric
version of his framework, the so-called fully
exible probabilities, in which he uses the discrete
version of the relative entropy. This time we consider l samples of an arbitrary market model
for the risk factors42 and assign a vector pxjI = (p1; ; pl) of probabilities for the scenarios43.
In fact, any vector of probabilities ep
= (ep1; ; epl) such that 0 epi 1 8i 2 f1; ; lg and Pl
i=1 epi = 1 de

281. nes a new probability measure e F 2 P
FxjI
, and we write the Kullback-Leibler's
42We describe an example of model in the next subsections, following a copula approach.
43In those scenarios are obtained with classical Monte-Carlo simulations, they can for instance be set as uniform
probabilities, that is pi
xjI = 1=l 8i 2 f1; ; lg.

282. The scenario-based approach 43
and Jensen-Shannon's divergences as
DKL
e F; FxjI
=
x
log
d e F
dFxjI
!
d e F
DJS
e F; FxjI
= DKL
e F;
FxjI + e F
2
!
+ DKL
FxjI ;
FxjI + e F
2
!
m (59)
bD
KL
ep; pxjI
=ep
log ep
log pxjI
;
bD
JS
ep; pxjI
= DKL
ep
;
ep
+ pxjI
2
+ DKL
pxjI ;
ep
+ pxjI
2
where 1 is a vector of ones (same size as ep
and pxjI). As for samples of the market, the joint
realizations are represented by an l N panel44 X of scenarios with probabilities pxjI , whereas
the focus of the views described in subsection 2.2, becomes a l K panel V of scenarios with
the same probabilities, that is
x fxjI )X
0
BB@
x1
...
xl
1
CCA
=
0
BB@
x1;1 x1;N
...
. . .
...
xl;1 xl;N
1
CCA
; pxjI
2
p1
664
...
pl
3
775
; (60)
v fvjI )V
0
BB@
v (x1)
...
v (xl)
1
CCA
=
0
BB@
v1 (x1) vK (x1)
...
. . .
...
v1 (xl) vK (xl)
1
CCA
; pxjI
2
p1
664
...
pl
3
775
: (61)
Within this framework, it is possible to represent most beliefs on the focus distribution conditional
on the private information set J as linear constraints on the new probabilities ep. For example,
views on expectations such as eE
(vkjI;J ) S mk can take the form
ep
V ;k
Xl
j=1
~pjVj;k S mk;
eE
eE
eE
where the investor speci

283. es his belief for mk. It is also possible to input qualitative views,
as ordered information like (v1jI;J ) (v2jI;J ) (vKjI;J ), represented by the
44Here, we have N = n + 3 for our three factors and n individual securities.

284. 44 Views Integration in Quantitative Portfolio Allocation
constraint
ep
(V ;k V ;k+1)
Xl
j=1
~pj (Vj;k Vj;k+1) 0;
for all k 2 f1; ;K 1g. A complete non-parametric speci

285. cation for views on volatilities, cor-relations,
lower/upper tail behavior and/or co-dependence, on the copula/marginal distributions
or even the complete joint distribution can be found in Meucci [47]. Furthermore, it is possible
to input views on scenario relevance (that is to give more weight to particular scenarios) through
the concepts of kernel mixing and fuzzy membership as in [51]. Without loss of generality, we
summarize K1
equality
and K2 inequality views using the formalism described above as a K1 l
matrix =
V f1; ;K1g;, a K1 1 vector , a K2 l matrix =
V
fK1+1; ;Kg; and a
K2 1 vector . Then the full-con

286. dence posterior ep
xjI;J is de

287. ned as
ep
xjI;J argmin
ep
2C
n
bD
s
ep
; pxjI
o
; (62)
where s 2 fKL; JSg and ep
2 C stands for probability measures satisfying the constraints, that
is
C
(
ep
ep
=
: (63)
4.4 Relative entropy minimization
The relative entropy minimization (62) under linear constraints (63) is a standard problem in
computer sciences that can be solved eciently by expressing it into the dual space. Because
of the convexity of the f-divergences and as we input only linear equality and inequality con-straints,
the non-linear programming problem satis

288. es the K.K.T. conditions45. Hence, the
duality gap of this optimization problem is zero, or equivalently there is no dierence between
the primal and dual optimal solutions. Thus the optimization only acts on a limited number
of Lagrange multipliers, equal to the number of constraints (or views), and can be solved e-
ciently even for a very large number of scenarios. In [47], Meucci recalls this solution for the
Kullback-Leibler's divergence. In appendix B, we extend this result to the symmetric Jensen-
Shannon's divergence. There is a close link between the Jensen-Shannon's divergence under K
45In non-linear programming, the Karush-Kuhn-Tucker conditions are the

289. rst-order necessary conditions for a
solution to be optimal, at least locally. In our case, the

290. rst-order conditions are even sucient (that is we do
not need to verify additional second-order conditions) and the solution of a programming problem with convex
objective and linear constraints is globally optimal.

291. The scenario-based approach 45
Lagrangian L
KL ep
(log ep
1 + ep
log p) + p1 ep
JS ep
log ep
log p+ep
2
+ p
log p log p+ep
2
+ ep
First order condition @L/@ epi = 0 8i 2 f1; ; lg
KL
PJ
j=1
j;ij + log
epi
pi
= 0
JS
PJ
j=1
j;ij + log
2epi
epi + pi
= 0
Statistics
KL epi = pie
XJ
j=1
j;ij
=) Maxwell-Boltzmann
JS epi = pi
e
XJ
j=1
j;ij
2 e
XJ
j=1
j;ij
=) Bose-Einstein
Table 4: Link between f-divergences and statistical mechanics, with a modi

292. ed Bose-Einstein statistics
whose condensation is shifted in log (1=2) for convenience in the numerical minimization.
liner constraints (k;ep
= k, for k 2 f1; ;Kg) and the Bose-Einstein's statistics (whereas
the Kullback-Leibler's divergence under the same constraints yields the Maxwell-Boltzmann's
statistics), which oers a physical rationale for views integration. We summarize this analogy
in table 4, where we derive both statistics from the minimization of the f-divergences (using
p pxjI for notational simplicity). Importantly, we modi

293. ed slightly the Jensen-Shannon's
PJ
divergence so that it retrieves the Kullback-Leibler's divergence if
j;ij 0, which corre-sponds
j=1
to views that do not alter much the initial probability measure. This means in fact that
the Kullback-Leibler's divergence is appropriate for common real-world applications when one
considers a market at equilibrium, in which case both minimizations yield (almost) the same
results46. In the case where one wishes to input views too far from Gaussian on the marginals,
the exponential twist provided by the two statistics derived from the classical entropy is insuf-

294. cient, as it has been shown in [23]. In the same paper, the authors provide a mathematical
46We veri

295. ed numerically that for most market views, then ep
JS ep
KL.

296. 46 Views Integration in Quantitative Portfolio Allocation
framework based on the

297. -Polynomial divergence47, closely related to the Tsallis entropy48, that
is appropriate for non-equilibrium systems. Furthermore, its dual formulation for the numerical
minimization and integration of market views is straightforward to compute (even though this
is not the author's preoccupation). However, these non-equilibrium systems are never observed
in practice, and most classical and neoclassical Economics and

298. nance theories (the CAPM we
cited is only an example) are concerned with market (at least) locally at equilibrium. This is
why we choose to use the Kullback-Leibler's divergence in the remainder of this thesis, keeping
in mind that some views may be inconsistent in the sense that no probability measure ep
can
satisfy the constraints in equation (63). Although this issue can be addressed by modifying the
constraints using a common linear programming correction procedure, this limitation has im-portant
theoretical consequences to which we will return later. As the sophisticated method we
introduced in the last few subsections is a numerical change of measure, we still need a
exible
way of modeling a market that we can then use to generate the required scenarios to numerically
bend the probabilities according to the investors views. This is why we set in what follows the
theoretical basics for a market model in order to perform the required Monte-Carlo simulations.
4.5 Copulas and flexible market models
Factor models allow one to concentrate on the marginal and joint modeling of less random vari-ables
than in the original problem (recalling that usually the number of factors L is smaller than
the number of risk-factors N). To model the dependence between factors, a realistic approach is
to use copulas: it corresponds to modelling separately the marginals and the dependence struc-ture.
Mathematically, a L-dimensional copula is a function C : [0; 1]L ! [0; 1] such that, for
u = (u1; ; uL) 2 [0; 1]L:
1. C (u) is increasing in each one of its components ui 8i 2 f1; ;Lg.
2. C (1; ; ui; ; 1) = ui and C (u) = 0 if at least one of the ui equals zero 8i 2 f1; ;Lg.
3. For all u1 = (u1;1; ; u1;L) 2 [0; 1]L and u2 = (u2;1; ; ; u2d) 2 [0; 1]d , u1;i u2;i
8i 2 f1; ;Lg, then
P2
j1=1
P2
jL=1 (1)j1++jL C (uj1;1; ; ujL;1) 0.
47Using the generator f(t) = t

299. +1 with

300. 0, it yields a divergence D

301. P
e F; FxjI
=
x
dFe
dFxjI

302. d e F, which
is linked to the Kullback-Leibler's divergence by the relation lim

303. !0
D

304. P (Fe;FxjI)1

305. = DKL
e F; FxjI
.
48We de

306. ne the relative Tsallis entropy with index

307. as DT

308. e F; FxjI
=
x
dfF
dFxjI

309. 1

310. d e F

311. The scenario-based approach 47
Moreover, if C is the distribution function of the random vector u = (u1; ; uL) 2 [0; 1]L,
we call survival copula of C, the distribution function C of the random vector 1 u (with 1
a L 1 vector of ones). Then, for any L-dimensional i.i.d. random vector z with its

312. ltered
probability space (
z;F; Pz) with It Ft 8t, Sklar's theorem guarantees the existence of a
copula Czt+1jIt : Ran Ran49 z1;t+1jIt zL;t+1jIt ! [0; 1]and its survival version Czt+1jIt :
1 Ranz1;t+1jIt
1 RanzL;t+1jIt
! [0; 1] such that, for all (z1; ; zL) 2
zt+1jIt ,
Fzt+1jIt (z1; ; zL) = Czt+1jIt
Fz1;t+1jIt(z1); ; FzL;t+1jIt(zL)
;
Fzt+1jIt (z1; ; zL) = Czt+1jIt
Fz1;t+1jIt(z1); ; FzL;t+1jIt(zL)
; (64)
which is unique if the marginals are continuous (which was an assumption in the

313. rst chapter). We
call Czt+1jIt and Czt+1jIt the copula and survival copula of zt+1 with respect to the information
publicly available at time t, which contains in fact all the dependence structure of the random
vector zt+1. In practice, it is often handy, as one can model separately the two components of the
multivariate distribution:

314. rst, one models
Fz1;t+1jIt(z1); ; FzL;t+1jIt(zL)
2 [0; 1]L instead of
(z1; ; zL) for all (z1; ; zL) 2
zt+1jIt , and then one chooses an appropriate copula for the
dependence structure.
4.5.1 Time-varying dynamics
It is well known that, additionally to co-dependence, most

315. nancial time-series exhibit volatility
clustering and time-varying dynamics (see

316. gure 12 above for an example), which violates a
necessary condition for Sklar's theorem to apply. This is why one usually starts with modeling
each factor's dynamics using an appropriate model to retrieve an i.i.d. sample of residuals. For
example, one of the most widely used process in Econometrics is the univariate GARCH(p,q) of
Bollerslev [12], which is de

317. ned as
yi;t = i + i;tzi;t;
2
i;t = !i +
Xp
j=1
j (yi;tj i)2 +
Xq
j=1

318. j2
i;tj ; (65)
where zi;t is the i.i.d residual process with zero mean and unit variance that we will model with
copulas. In

319. gure 13 next page, we show that a GARCH(1,1)

320. lter is often sucient to
capture the time-varying dynamics. In what follows, we assume that the GARCH(1,1) allowed
49Ranzi;t+1jIt = Fzi;t+1jIt(
zi;t+1jIt ) 2 [0; 1] is the range of the marginal distribution for all i 2 f1; ;Lg.

321. 48 Views Integration in Quantitative Portfolio Allocation
2000 2002 2004 2006 2008 2010 2012
−0.15 −0.05 0.05
t [week]
Return
Market factor
0 10 20 30 40 50
0.0 0.2 0.4 0.6 0.8 1.0
Lag [week]
ACF of squarred return
2000 2002 2004 2006 2008 2010 2012
−0.06 −0.02 0.02 0.06
t [week]
Return
SMB factor
0 10 20 30 40 50
0.0 0.2 0.4 0.6 0.8 1.0
Lag [week]
ACF of squarred return
2000 2002 2004 2006 2008 2010 2012
−0.05 0.00 0.05 0.10
t [week]
Return
HML factor
0 10 20 30 40 50
0.0 0.2 0.4 0.6 0.8 1.0
Lag [week]
ACF of squarred return
Figure 12: As an example, we show the weekly returns on the three factors for our market model. There
are periods of high volatility, that is periods with many extreme (both positive and negative) returns, and
period of low volatility. Furthermore, as the autocorrelation function of the squared returns (a proxy for
the realized volatility) exhibits a slow decay, there is some degree of predictability in the volatility (see
[53] for instance). Those features contredicts the i.i.d. assumption of Sklar's theorem and this is why we
use model for returns to capture them.

322. The scenario-based approach 49
0 100 200 300 400 500 600
−4 −2 0 2
t [week]
Return
Market factor
0 10 20 30 40 50
0.0 0.2 0.4 0.6 0.8 1.0
Lag [week]
ACF of squarred return
0 100 200 300 400 500 600
−4 −2 0 2
t [week]
Return
SMB factor
0 10 20 30 40 50
0.0 0.2 0.4 0.6 0.8 1.0
Lag [week]
ACF of squarred return
0 100 200 300 400 500 600
−4 −2 0 2 4 6 8
t [week]
Return
HML factor
0 10 20 30 40 50
0.0 0.2 0.4 0.6 0.8 1.0
Lag [week]
ACF of squarred return
Figure 13: As an example, we show the weekly residuals zi;t from the GARCH(1,1) model applied to our
three factors. We observe that the residuals do not show volatility clustering, or equivalently that their
squared values are not autocorrelated anymore.

323. 50 Views Integration in Quantitative Portfolio Allocation
Name b b! b b

324. Market 2:50 103 2:34 105 1:73 101 8:11 101
SMB 0:73 103 6:34 106 8:86 102 8:76 101
HML 1:01 103 2:95 106 1:02 101 8:87 101
Table 5: Parameters for the GARCH(1,1)

325. t: the estimation is performed using quasi-maximum likeli-
hood maximization, which assumes normal distribution for the residuals and uses robust standard errors
for inference (see Bollerslev [13]). The implementation is provided in the R package fGARCH.
us to retrieve (closer to) i.i.d. residual processes50 bzi;k 8i 2 f1; ;Lg and 8k 2 ]t T; t[, a
(T + 1) L sample thus satisfying conditions for Skylar's theorem to apply, and show how it is
possible to model their multivariate distribution.
4.5.2 Some useful copulas
Because the theory about copulas is very rich and goes far beyond the scope of this work, we
will give here only a few illustrative examples and will refer for instance to [46] from which we
inspired ourselves. The simplest copula (from the fundamental-copulas family) is probably the
independence copula, de

326. ned trivially by assuming
Czt+1jIt
Fz1;t+1jIt(z1); ; FzL;t+1jIt(zL)
=
YL
i=1
Fzi;t+1jIt(zi); (66)
that is the joint distribution is the product of the independent marginals. As we emphasized
in the precedent subsection, this copula may be useful to describe the residuals from the factor
model described by equation (20) (after removal of their time-varying dynamics). However, it is
most often inadequate for dependent random variables, which is usually the case for the residuals
retrieved from the GARCH(1,1)

327. t on the factors themselves. This is why we will present another
family of copulas very convenient to use and to understand: the family of implicit-copulas, that
is copulas implied by a known parametric multivariate distribution. The most widely used in
this family (before the recent crisis) is the Gaussian copula, where we assume a multivariate
50Although they are only closer to i.i.d than the original processes, we will assume that the capture of the
volatility clustering is enough. As one should in principle check the autocorrelation for all the moments of the
distribution, the i.i.d property is very dicult to verify in practice.

328. The scenario-based approach 51
normal C
51 with correlation matrix C for the dependence structure, that is
Czt+1jIt
= C
Fz1;t+1jIt(z1); ; FzL;t+1jIt(zL)
1
; ; 1
Fz1;t+1jIt(z1)
FzL;t+1jIt(zL)
:
(67)
As we show in

329. gure 14 however, the marginal distributions of our residuals exhibit fat tails
that are not present in the multivariate normal. This is why we will also cite here the student
copula with degrees of freedom and correlation matrix C, which is de

330. ned as the Gaussian
copula structure as
Czt+1jIt
= t;C
Fz1;t+1jIt(z1); ; FzL;t+1jIt(zL)
t1
Fz1;t+1jIt(z1)
; ; t1
FzL;t+1jIt(zL)
;
(68)
where t and t;C are the univariate and multivariate student distributions. Additionally to fat
Figure 14: The quantiles of the residuals are plotted against Gaussian quantiles, showing deviations,
the so-called fat-tails, on both negative and positive sides.
tailed marginals, extreme events often come at the same time for dependent random variables
in the

331. nancial context: for instance, during the recent sub-primes

332. nancial crisis, many stocks
prices felt at the same time. This concept of extreme co-movements between random variables
51For a bivariate normal random vector x = (x1; x2), with correlation coecient , we de

333. ne
1 (u1) ;1 (u2)
= P ( (x1) u1;(x2) u2) =
1(u1)
1
1(u2)
1
exp
(s21
2s1s2s22
)
2(12)
2 (1 2)1=2
ds1ds2;
with the standard univariate normal distribution function. Then, C is the generalization of for L dimensions.

334. 52 Views Integration in Quantitative Portfolio Allocation
can be described for instance using the tail dependence parameters. Considering a bivariate
random vector x = (x1; x2) with marginals F1 and F2, and copula C and survival copula C, the
upper and lower tail dependence parameters are de

335. ned as
u (x1; x2) = lim
q!1
P
X2 F1
2 (q)

337. X1 F1
1 (q)
= lim
q!1
P
X2 F1
2 (q) ;X1 F1
1 (q)
P
X1 F1
1 (q)
= lim
q!1
C (1 q; 1 q)
1 q
= lim
q!0+
C (q; q)
q
;
l (x1; x2) = lim
q!0+
P
X2 F1
2 (q)

339. X1 F1
1 (q)
= lim
q!0+
P
X2 F1
2 (q) ;X1 F1
1 (q)
P
X1 F1
1 (q)
= lim
q!0+
C (q; q)
q
; (69)
with u (x1; x2) = l (x1; x2) = (x1; x2) because C = C for radially symmetric copulas52. As
elliptical distributions53 are radially symmetric around their mean-vector, both the Gaussian and
student copulas also have this property. Furthermore, an application of L'H^opital rule to radially
symmetric copulas yields
(x1; x2) = lim
q!0+
C (q; q)
q
= lim
q!0+
dC (q; q)
dq
= lim
q!0+
P
X2 F1

341. 2 (q)
X1 = F1
1 (q)
+ lim
q!0+
P
X1 F1

343. 1 (q)
X2 = F1
2 (q)
= 2 lim
q!0+
P
X2 F1

345. 2 (q)
X1 = F1
1 (q)
;
(70)
where we used @
@q1
C (q1; q2) = lim
!0
C(q1+;q2)C(q1;q2)
= P (F (X2) q2j F (X1) = q1) for the third
equality. In the Gaussian
case with
a correlation coecient , as we can express the conditional
distribution x2jx1=x N
x; 1 2
, we have (x1; x2) = 2 lim
x!1
x
p
1 =
p
1 +
= 0, that
is no asymptotic dependence in the tails.
For p
the student copula with degrees of freedom, a
p
similar argument yields (x1; x2) = 2t+1
( + 1) (1 )=
1 +
. We thus observe that,
provided 154 and 1, the student distribution is asymptotically dependent in both
tails.
L if and only if x d=
x.
52A random vector x = (x1; ; xL) is said to be radially symmetric around 2 R
Thus, a random vector u = (u1; ; uL) 2 [0; 1]L with a copula C as distribution function can only be radially
symmetric if and only if u d=
1 u (with 1 a L 1 vector of ones), also implying C = C.
53Elliptical distributions were de

346. ned in a footnote of subsection 3.3.
54Otherwise we have lim
t .
!1

347. The scenario-based approach 53
4.5.3 Dependence structure estimation
For the sample period ]t T; t[ used to estimate the factor model described by equation (20) and
the GARCH(1,1) from equation (65), we consider the (assumed) i.i.d sample
bz =
0
BB@
bztT;1 bztT;L
...
...
...
bzt;1 bzt;L
1
CCA
; (71)
where bzi;k denotes the estimated residual from a dynamic model 8i 2 f1; ;Lg and 8k 2
]t T; t[. With this sample, there exists a fully parametric and a semi-parametric approach
to model the dependence structure with parametric copulas. The

348. rst approach consists in

349. tting marginals b Fyi;t+1jIt with suitable parametric models and then using them, one can obtain
a sample
bu
=
0
BB@
butT;1 butT;L
...
...
...
but;1 but;L
1
CCA
; (72)
where bui;k = b Fyi;t+1jIt(bzi;k) are the so-called pseudo-observations for all i 2 f1; ;Lg and
8k 2 ]t T; t[. The second approach uses directly the empirical marginals to get the sample
bu, that is we de

350. ne bui;k =
PT
s=0
1
T+21Ibzi;tsbzi;k (with 1Ix the indicator function taking 1 if x
is true and 0 otherwise) for all i 2 f1; ;Lg and 8k 2 ]t T; t[. This last approach is shown
−3 −2 −1 0 1 2
0.0 0.2 0.4 0.6 0.8 1.0
conversion to pseudo−observations
z
u
0.0 0.2 0.4 0.6 0.8 1.0
−3 −2 −1 0 1 2
CMA combination
u
z
Figure 15: conversion to pseudo observations and copula-marginal algorithm combination step
on the left-hand side of

351. gure 15, where we sampled 20 observations from a standard normal

352. 54 Views Integration in Quantitative Portfolio Allocation
distribution and converted them into pseudo-observations. Our next step, with both approaches,
is then to use the sample bu
to

353. t a parametric copula. In many cases, the easiest way to cope
with low-dimensional problems (which is the case with our three factors) is a maximum likelihood
estimation, that is to

354. nd the set of parameters b such that
b argmax
lnL() ;
lnL() =
XT
k=0
lnc (bu1;tk ; buL;tk) ;
c (bu1;tk ; buL;tk) =
@C (u1; ; uL)
@u1 @uL

358. bu1;tk ;buL;tk
; (73)
where C is the copula one wants to

359. t. For more details about the so-called inference-functions
for margins approach (that is the method where the marginals are

360. rst parametrically esti-mated),
we refer to Joe [38]. In the following example, we used the so-called pseudo-likelihood
Name Residuals Gaussian CI t CI
Market/SMB 0:240 0:245 [0:166; 0:326] 0:250 [0:173; 0:323]
Market/HML 0:036 0:051 [0:140; 0:042] 0:045 [0:136; 0:048]
SMB/HML 0:048 0:060 [0:145; 0:027] 0:090 [0:176;0:002]
Table 6: Correlations between the residuals from the GARCH(1,1) and those estimated by

361. tting copulas,
whose implementation is provided in the R package copula. We bootstrapped the estimation using ordinary
non-parametric bootstrap provided in the R package boot. Then we applied the Anderson-Darling, Cramer-
Von Mises, Kolmogorov-Smirnov and Pearson 2 tests and couldn't reject the normality hypothesis at
95% for the bootstrapped statistics, so we used Gaussian con

362. dence intervals.
(semi-parametric) approach described for example in [32]. In table 6, we present the correlation
parameters. We observe

363. rst that, as expected from their construction, the three factors are
not much correlated. In fact, with a noise level at 2=
p
672 = 0:077, we see that only the

364. rst
coecient is really signi

365. cant: when the market goes well, there is an in
ux of capital toward
small

366. rms which outperform large ones (and conversely when the market goes down). Moreover,
we observe that both copulas seem to capture the dependence in the residuals, as the original
correlations always fall within the bootstrapped con

367. dence intervals. It should also be noted that
the maximized likelihood of the Gaussian copula is 21:86, whereas that of the student copula
is more than twice as much with a maximized likelihood of 45:07, and we thus will prefer the
student copula. There are two other reasons for this choice:

368. rst the fat-tail and asymptotic tail
dependence properties we emphasized earlier, and second, even an identity correlation matrix C
wouldn't mean independence between the factors, provided that 155, which is the case here
55Otherwise we would have the independence copula for uncorrelated variables.

369. The scenario-based approach 55
Market
0.0 0.2 0.4 0.6 0.8 1.0
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
0.0 0.2 0.4 0.6 0.8 1.0
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
0.0 0.2 0.4 0.6 0.8 1.0
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
SMB
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
0.0 0.2 0.4 0.6 0.8 1.0
l
l
l l
l
l l
l
l
l
l l
l l
l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
0.0 0.2 0.4 0.6 0.8 1.0
0.0 0.2 0.4 0.6 0.8 1.0
HML
Original pseudo−observations
Market
0.0 0.2 0.4 0.6 0.8 1.0
l l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l l
l
l
l l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
0.0 0.2 0.4 0.6 0.8 1.0
l l
l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
0.0 0.2 0.4 0.6 0.8 1.0
l
l l l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
SMB
l
l
l l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
0.0 0.2 0.4 0.6 0.8 1.0
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
0.0 0.2 0.4 0.6 0.8 1.0
0.0 0.2 0.4 0.6 0.8 1.0
HML
Simulated pseudo−observations
Figure 16: Original and simulated (from the t copula) pseudo-samples.
with an estimated b = 5:45 and b 2 [3:995; 8:411] at 95%. For this parameter, the statistics show
a large positive skew and we could reject the normality hypothesis at 95% with the four tests of

370. gure 6. Thus we used adjusted bootstrap percentile (see [24, 25]) whose implementation. To
understand the origin of the skew, we

371. tted the copula using a 100-week moving window and
observed that there is a 20 30 week window at the peak of the sub-prime crisis where this
parameter becomes very unstable (b moves from 5 to more than 120 in less than three weeks). In
fact, this period creates instabilities in the parameter estimation and leads to the large positive
skews in the bootstrapped statistics. If one think in terms of common-sense, the returns of our
three factors may not be much linearly correlated, but they may be tail-dependent. For example
during crises, the three factors may exhibit large negative value at the same time as all prices
fall.
4.5.4 Closing the model
With our estimated copula, Monte Carlo simulations can be performed to obtain a new sample
of pseudo-observations of any size (see [46] for details on student copula simulations). In

372. gure
16, we show the original pseudo-sample, as well as a new pseudo-sample
bu
s =
0
BB@
bus
1;1 bus
1;L
...
...
...
busl
;1 busl
;L
1
CCA
; (74)
simulated with three times as many pseudo-observations. Finally, a very convenient way to
convert the simulated pseudo-samples into a simulated sample of observations is the combination

373. 56 Views Integration in Quantitative Portfolio Allocation
step of the copula-marginal algorithm of Meucci [50]. It pairs for each factor the observations
and pseudo-observations f(bz;1;bu
;1) ; ; (bz;L;bu
;L)g and reverse them to obtain (bu
;i; bz;i) for
each i 2 f1; ;Lg. Then it maps bu
s
;i into bzs
;i by linear extrapolation using (bu
;i; bz;i) for each
i 2 f1; ;Lg to obtain
bzs =
0
BB@
bzs
1;1 bzs
1;L
...
...
...
bzs
l;1 bzs
l;L
1
CCA
: (75)
We show an example of this mapping in the right-hand side of

374. gure 15, where we simulated 4
Market
−4 −2 0 2
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
ll
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
−4 −2 0 2
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
lll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
−4 −2 0 2
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
SMB
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
−4 −2 0 2
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l ll
l
ll l
l
l
l l
ll
l
l
l
l
ll
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l ll
l
l
l ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
ll
l
ll
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l l ll
l
l
l l
l
l l l
l
l
l
l l l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll l l
l
l l l
l
l
l
l
l
l
l
l
l
ll l
l
l l l
l l
l
l
l l
l
l
l
l
l
l
ll
l l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
ll l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
ll
l
l l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
ll l
l
l
l l
ll
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
ll l
l
l
l l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
ll
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
ll
l
l l l
l
l
l
l l l
l
l
ll
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l l
l
l l l
l
l
l
l
l
l
l
l
l
l l l
l
l l l
ll
l
l
ll
l
l
l
l
l
l
l l
l l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l l l
l
l
l
−4 −2 0 2 4 6 8
−4 −2 0 2 4 6 8
HML
original
Market
−4 −2 0 2 4
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
ll
l
l
l
l
l
l
l
l
ll l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
lll l l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l l
l
l
ll
l
l
l
ll
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l l ll
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
ll
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
ll
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll l
ll
l l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l ll
l
l
l
l
l
l
l
l
l
l l
l ll
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
ll
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll l l
l
l
l
l
l
l
l l
l
l l
l l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l l ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
ll l
l
ll
l ll
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l l
ll
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
lll
l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l lll
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l l l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
ll
l l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l ll
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
ll
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
ll
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l l
ll
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
llll
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
ll l
l
l l
l
l l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l l
l l
l l l
l
l
l
l
l
l
l l l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
ll
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
lll
ll
l
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
lll
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l ll l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l ll
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
ll
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
ll
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l l
l
l
l
l
l
ll
l
l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l l l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l l
l
ll
l
l l
l
l
l
l
l
l
l
l
l l
l l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
ll
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
−4 −2 0 2
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l ll
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l ll l l
l
l l
ll
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
lll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
ll l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l l
l
l
l l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l ll
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
ll
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l l
ll
l
l
l
l
l
l
l l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l lll
l
l
l
l
l
l
l
l
l
ll
ll l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
lll
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
ll
l l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l l
l
l
l
l
l
l
l l
l
ll
ll
l
l ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
llll l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
ll
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l ll
l
l l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l l
ll
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
ll
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
llll
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
ll l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
ll
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l l
l l
l l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l ll
l
l
l
l l
ll
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l ll
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
lll
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l
l
l
l l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
ll
l l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
ll l
l
ll
l
l l
l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
lll
l l
l l l
l
l
l
l
l
l
l l l
l
l
l
l lll
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l l
ll
l
l
l
l
l
ll
l
l l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll ll
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
lll
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
lll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l ll
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
ll
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
ll
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l ll
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
ll
l
l
l
l
l
l
ll
l
l
ll
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
ll l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
ll
l
l
l
l
l
ll
l
l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l lll
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
ll
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
ll
l
ll
l
l l
l
l
l
l
l
l
l
l
ll
ll
l
l l
ll l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
ll
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
−4 −2 0 2 4
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l l
l
l l
l
l l
l
l
ll
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l l
l
l
l l
l
l
ll
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
ll
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
ll l
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
lll
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
ll
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l l
l
l
l
l ll l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
lll
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
ll
l
l
l
l
l
l
ll
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l l
l
lll
l
l
l
l l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
ll
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l l
l
ll
l l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
ll
l
l
l ll
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
ll
l
ll
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
ll
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
ll l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l l
l
ll
l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
ll ll
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l l
l
l
l
l
l
l l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l l
l
l
l
l
l
l
l l
l l
l l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
SMB l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
ll
l
l l
l
l l
l
ll
l
l
ll
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
lll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l l
l
l
l l
l
l
l l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
lll
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
lll
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
lll
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
ll
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l
l l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
lll
l
l
l
lll l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l l
l
l
l
ll
l
l
l
l
l
l
ll
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l l
l
l
l l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l
l l
l l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
ll
l
l
l
l
ll
ll
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
ll
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
ll
l l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
ll
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l l l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
ll
l
ll
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
ll
l
ll
l
l
l
l
l l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
ll
l
l l
l
l l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
lll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
ll
l
l
l l
l
ll
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
ll l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l ll l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
ll
l
l l
l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
ll ll
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l ll
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
ll
l
l
l
l
ll
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
lll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
ll
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l lll
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l l
l l
l l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l l
ll l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
−4 −2 0 2
l l
l
l l l
l
l l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l l l
l
l l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
ll l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l l
l
l
l
l
l
l l
l
l
l
l
ll l
l
l
l l l
l l
l l
l l
ll
l l
l l l
l
l
l
l
ll l
l
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l l l
l
l
l
l
ll l
l
l
l
l l
ll
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l l
l
lll ll
l
l
ll
l
l ll
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l ll
l
l
l
l
l l
l
l
l l
l
l
l
ll l l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l ll
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l l
l
ll
l
l l l l
l
ll l
l l
l
l l
l
l
l l ll l
l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l ll
l
l
l
l
l
l l
l l
l
l
l
ll
l
l
l
l
l
l l l
l
l l
l l
l l l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l l
ll
l
l
l l
l l l
l
l
l
l
l l
l l
l
l
l
l
ll
l
l
l
l ll l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l l l
l l l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l ll l
l
l
l
l l
l
l l
l
ll
l
l
l l
l
l
l
l l
ll ll
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
ll l
l
l
l l
l
l
l
l
l l
l ll
l
l
l
ll
l
l l l
l
ll
l ll
l
l
l
l
l
l
ll
l
l
l
ll l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l ll
l
l
l
l l
l
l
l l l
l l
ll
l
l l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l l l
l
l
l
l
l ll l
l
ll
l
l
l
l
l
l
l l
l l
l
l
l
l l
l
l l
l l
l
l
l
l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l ll
ll
l
l l l
l
l
l
l
l
l
l
ll
l
l
l l
l l
l l
l
l
l l
l
l
l
l
l l l l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l l
l
l l
l
l
l
l
l l
ll l
l
l
l
l
l
l
l l
l
l
l l
l l l
l l
l
l
l l
l
l
l
l
l
l ll l l
l
l
l
l
l
l
l
l l l l
l
l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l l
l l
l
ll
l l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
ll
l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l l
ll
l l
l
l
l
l
ll
l
l
l
l l
ll
l
l l
ll
l l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l l l l l
l
l l
l
l
l
l
l
l
l ll l
l
ll
l l
l
l
l
l
l l
ll ll l
l
l
l
l
l
l
l l
l
l
l
l
l
l l lll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l l
ll
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l l l ll
l
ll
l
l l
l
l l
l
l
l
l
l
l
l
l l l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
ll
l
l ll
l
l l
l l
l
l
l
l l
l
l
l l ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
ll
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l ll
l ll
l
l
l
l l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l l l
l
l
l l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l llll
ll l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l l
ll l
l
l l
l l
l
l
l
l
l
l
ll
l
l
l
l
l l l l l
ll l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l l l
l
l l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
lll l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l l
l l l
l l
l
l
l l
l
l l
l
ll
ll
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
llll
l
l
l l
l
l l
l
l
l
ll
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l ll l
l
l ll
l
l l l
l
l
l l
l
l
l l
l
l
l
l l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l l
l
l
l
l
l l ll
l
l
l
ll l l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
ll ll
l
l
l
l
l
l
l
l
l ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll lll
l
l
ll l
l
l
l l
l
l l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
ll
l
ll
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
ll l l l
l
l
ll
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
ll
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l l l
l
lll
l
l
l
l
l
l l
l l
l
l l l
l
l
l
l l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l lll
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
ll l
l
l
l
l ll
l
l
l
l l
l
l
l ll
l
l
l
l
l
l
l
l
l
l l
l l
ll
l
l
l
l l
l
l
l
l
l l l
l
l l ll
l
l ll l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l l
l l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
lll
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
ll l
l
l
l
l
l
l
ll
l l l l l l
l
l
l l
l l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l ll
l
l
l
l
l
l l
l
l
l
l
l
l
l l l
l
l l
l
l
l
l ll
l
l
l l
l
l
l
l
l l
l
l
l
l l l l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
ll l l
l
l
l
l
l
l
l
l
l l
l l l l
l
l l
l l
l
ll l
l
l
l ll l
l
l
l l
l
l
l
l l
l
l
l
l l l
l
l l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
ll
l l
l
l l
l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll ll
l
l l l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l l l
l
l
l
l
l l
l
l l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l l l
l
l
l
l
l l l ll
l
l l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l l l ll
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l ll l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l l l
l
l
l
l l
l
l ll
ll l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
ll l
l
l
l
lll
l
l
l l
l
l
l
l l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l ll
l
l
l
l l
l
l
l
l l
l
l
l l
ll ll l
l
l
l
l
l
l
l
l
l
l
l l
l ll
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
lll l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l l
l
l l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l
ll l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l l
l l
l
l
l l ll
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
ll l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l l
l l
l l l l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
ll
ll
ll l
l l
ll l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
ll l
l l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l l
l
l
l
l l
l l
ll
l
l
l
l ll
ll l
l
l
l l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l l
l
l llll l
l
l l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l ll
ll
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l l
l l
l
l
l
l
l
l l
l l
l
l
ll
l l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
ll
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l lll
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l l
l l
l
l
l l l
l
l
l
l
l
l l
l
l
l
l
ll
l
l l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l l
l
l
l
l l
l
l
ll l
l
l
l
l
l
l
l
l
ll l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l l
l
l l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
lll
l
l
l l
l
l
l
l l l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l l l
l
l
l
l l
l l ll
l ll
l
l
l
l
l
l
l
l l
l l
l
l
l
ll l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
ll l l
l
l
l l
l
l l
ll
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l l
l
l
lll l
l l l
l
l l
l
l l
ll
l
l
l
ll
l l lll l
l l
l
l
l l
l
l
l l
l
ll
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l l l ll
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l ll l
l
l
l
l
l l l
l
l l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l ll
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
ll
l
l
l
l l
l l
l
l l
ll l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
ll
l l
l
l l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
ll
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l l
l l l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l l l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l ll
l
ll l
l
l
l l
l
l
l
l l
ll l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l l
l
ll
l
l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l l
l
ll
l
l
l
l
l
l l
l l
l ll
l
l
l
l
l
l
l
l
l
l
l
l l l ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l ll
l
l
l
l
l l
l
l ll
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
l ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l l
l
l
l
l
ll l
l l
l
l l
l
l
l
l
l
l
ll ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l l
l
ll
l
l
l l
l
l l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll l
l l
l
l
l l
l
l
l
l
l
l l
l
l
ll
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l l
l
l
l
l
l
lll l
l
l
l
l
l
l l
l
l
l
l l
l l
l
l
l
ll l
l
l l
l
l
l
l l ll
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l l
l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
ll l l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l ll l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l l
l
l
l
l
ll l
l
l
l
l
ll
l
l
l
l
l
l
l
ll
l
l l
l l l
l
l
l l
l
l
l
l
l
l
l
l
l
ll l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l l l
l
l
l ll
l
l
l
l
l l l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l lll l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l l
l
l
l
ll
l
l l
l l lll
ll
l l
l
l
l
l
l
ll
l l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l l l
l l
l l
l l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l ll
l
l
l
l l
l
l
l
l
l l l
l
l l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
ll
l
l
l l
l
l
ll l
l
lll
l l
l
l
l l ll
l l
l
l l
l
l ll
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
ll
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l l
ll
l lll
l
l
l
l
l
l
l
l
l
l
l l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
ll
l
l
l
l
l
l
l
l
l
l lll
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l l l
l
l l
l
l l
l l l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l ll l l
l l
l
l
l
l
l
l
l
l
l
l
ll
l ll
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
lll l
l
l
l
l
l
l
lll
l
l l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l ll
l l
l
l
l
l l
l l l
l
l
l
l
ll
l
l
ll
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l
l l
l
l
ll l
l l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l l ll
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l l l
l
l
l l
l l
l
lll
l l l
ll
l
l
l
l l
l
l
l l
llll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l l l
lll
l l
l
l
l
l
l llll l
l
l
ll
l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l l l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l l
l l
l
l
l
l
l
l l l
l
ll l
l
l l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l ll
l
l
l
l
l
l
ll
l
l
l l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l ll l l l
l
l l
l
l
l
l
l
l l
l l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l l
l
l
l
l l l
l
l
l l
l
l l
ll
l l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
ll
l l
l ll
l
l
l
l
l
l
l
l
l
l
l ll l
l
l
l l l
l l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
ll
l l
l
l
l
l
l
l l l
l
l
l
l
ll
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l l
l l
l l
l
ll l
l l
l
l
l l l
l
l
l l l l
l
l
l
l
l
l l l
l
l
ll
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l ll
l l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l l
l
l l
l
l ll
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l l l
l
l l l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
ll
l
ll
l
ll
l
l l
l l l
l l
l
l
l l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
ll
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
ll l
ll
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l
ll l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l l l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
lll l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll ll
l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l l
l
l
l
l l l
l
l
l ll
l
l
l
l
l
l
l
ll
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
ll
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l ll
l ll
l
l
l
l l
l
l l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l l
l
l l l
ll
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l ll
l l
l
l
ll
l
l l
l
l
ll
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
lll ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll l l
l
l
l
l
l l
l
l l l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l l
l
l
l
l
l l l l l
ll l
l
l
l
l
l
l l ll
l l
l
ll
l l
l l l
l
l
l
l
l
l
l
l
l
l
l ll
l l
l
l
l l
l
l
l
l
l l
ll
l
l
l l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l l l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
lll
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l
l l
l
l
l l
l l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l ll
l
l l
l
l
l
l
l
l
l
l
l l l l
l l l
ll
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l l
ll
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l ll
l
l
l
l l
l
l
l l
l
l l
l
l
l
l l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l ll
l l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
ll
ll
l
l l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l
l
ll
l
l
l
l l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l lll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll l l
l
l
l
l ll
l ll
l
l ll
l
l l
l
l
l l
l
ll
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
ll l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l l
l l ll
l
l l
l
l l
l
l l
ll
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l l l l
l l
l
l
l
l
l
l l l
l
l
l l
l
l l ll
l
lll
l l
l l
l l
l
l
l
l lll
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l l
l
l l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l ll
l
l l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l ll
l
l l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l ll l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l l
l
l
l
l
l
l l
l
l
l
l
l ll
l
l
l l l
l l
l
l l
l l
l l
l l l
l
l
l
l
l l l
l
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l l l
l
l
l
l
ll l
l
l
l
l l
l l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l llll
l
l
l l
l
l ll
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l
l ll
l
l
l
l
ll
l
l
l l
l
l
l
l ll l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l ll
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
ll
l l
l
ll
l
lll l l
l
l l l
l l
l
l l
l
l
l l ll l
l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll l l
l
l
l
l
l
l l
l l
l
l
l
ll
l
l
l
l
l
l l l
l
ll
l l
l l l
l
l
l
l
l
l
l
l
l
ll
l
l ll
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l l
ll
l
l
l l
l ll
l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
ll ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l ll l
l l l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l ll
l
l
l
l l
l
l l
l
l l
l
l
l l
l
l
l
ll
l l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l l
l
l
l
l
l l
l l l
l
l
l
l l
l
l l l
l
ll
l ll
l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l l l
l l
l l
l
l l
l
l
l l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
ll l l
l
l
l
l
l ll l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l
l l
l l
l
l
l
l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l l l
l l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l l
l l
l l
l
l
l l
l
l
l
l
l l l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l l
l
l l
l
l
l
l
l l
l l l
l
l
l
l
l
l
ll
l
l
l l
l l l
l l
l
l
l l
l
l
l
l
l
l l l l l
l
l
l
l
l
l
l
l l ll
l
l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l ll
l l
l
l
l
l
l
l
l
l l
l l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
ll
l l
l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l l
l
l
l
l
l
l
ll l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l l
l ll
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l l
l l
l l
l
l
l
l
l l
l
l
l
ll
l l
l
ll
l l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l ll l l
l
l l l
l
l
l
l
l
l
l l ll
l
l l
ll
l
l
l
l
l l
l ll ll
l
l
l
l
l
l
l l
l
l
l
l
l
l l ll l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
ll
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l ll l l
l
ll
l
l l
l
l l
l
l
l
l
l
l
l
l l l
l
ll
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l l
l
l ll
l
l l
l l
l
l
l
ll
l
l
llll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l l
l
l
ll l
l
l
l
l
l l l
l l l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
ll l
l
l
l l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l lll l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
ll
l l l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l l l l
l l l
l
l
l l
l
l
l
ll
l
l l
l
l
l
l
l
l l
l
l
l
l
l
ll ll
l
ll l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l l
l l l
l l
l
l
ll
l
l l
l
l l
l l
l
l
l
l
l l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l lll
l
l
l l
l
l l
l
l
l
l l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l l
l lll
l
ll l
l
ll l
l
l
l l
l
l
l l
l
l
l
l l
l l
l
l l l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l l
l
l
l
l
lll l
l
l
l
ll l l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l lll
l
l
l
l
l
l
l
l
l lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
llllll
l
l
l l l
l
l
l l
l
l ll
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l l
l
ll
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l l ll l
l
l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
ll
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
ll l
l
ll l
l
l
l
l
l
l l
l l
l
l l l
l
l
l
l l
ll
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
ll
l
l
l
l
l l
l l
l l ll
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l l l
l
l
l
l ll
l
l
l
l l
l
l
l l ll
l
l
l
l
l
l
l
l
l
l l
l l
l l
l
l
l
l l
l
l
l
l
l l l
l
l ll l
l
l l ll
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l l
l l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
ll l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l l l l l l
l
l
l l
l l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l l
l
l l
l
l
l
ll l
l
l
l l
l
l
l
l
l l
l
l
l
l ll l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l l
l l ll
l
l
l l
l
l l l
l
l
l l l l
l
l
ll
l
l
l
l l
l
l
l
l l l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l l
l
l l
l l
l
ll
l
l
l
l
ll
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
ll l
l
l
l
l
ll
l
l l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
ll ll
l
l
l
l
ll l l l
l
l l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l l l l l
l
l
l
l
l
l
ll
l
l
l
l l
l
l l
l
l
l
l
l l l l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
lll l
l
l
l
ll
l
l ll
l l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
ll
l
l
l
l
l
l
ll l
l
l
l
l ll
l
l
ll
l
l
l
l l l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll l
l
l
l
ll
l
l
l
l l
l
l
l l
lll l l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l ll l
l
l
l
l
l l
l
ll
l
l l
l
l
l
l l
l
ll l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l l l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l l
l l
l
l
l lll
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
lll
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l l l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l l
l l
l ll
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l l l
l l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l l
l
l
l
l l
l l
l l
l
l
l
l l l
l l l
l
l
l l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
ll
l
l l
l
l
l
l
l
l l
l
l
ll
l
l
l l
ll
l
l
l
l
l
l
l l
l
l
l
l
l l l
l
l lll l l
l
ll
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l ll
ll
l
l
l
l
l
l
l
l
l
l
ll l
l l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll l
l l
l
l
l
l
l
l l
l l
l
l
l l
l l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l
l l l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l l
l l
l
l
l l l
l
l
l
l
l
l l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
ll
l
l
l
l
l l
l
l
l
l l
l
l
ll l
l
l
l
l
l
l
l
l
l ll
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l l
l
l l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
lll
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l ll
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l l
l
l
l
ll l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll l
l l l
l
l
l
l l
l l l l
ll l
l
l
l
l
l
l
l
l l
l l
l
l
l
ll l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll l l
l
l
l l
l
l l
ll
l
l l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
ll
l
l
l lll
l l l
l
ll
l
l l
l l
l
l
l
ll
lll ll l
l l
l
l
l l
l
l
l l
l
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l ll l l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l ll l
l
l
l
l
l ll
l
l l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l l
l
l l
ll l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l l
l l
l
l l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l l
l l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l l l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l l
l
l
l
ll
l l l
l
l l l
l
l
l l
l
l
l
ll
l l l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l l
l
l
l
l
l
ll
l
l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l l
ll
l l l
l
l
l
l
l
l
l
l
l
l
l
llll l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
lll
l
l
l
l
l l
l
l ll
l
l
l
lll
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l l
l
l
l
l
l l l
l l
l
l l
l
l
l
l
l
l
l ll l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l l
l
l
l
l
l l
l
l l
l
l
l l
l
ll l
l
l
l
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l ll
l l
l
l
l l
l
l
l
l
l
l l
l
l
l l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
ll
l
l
l
l
l
l l l
l
l
l
l
l
ll
l
l
l
l l
l l
l
l
l
l ll
l
l l
l
l
l
l ll l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l l
l
l
ll
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l l l l
l
l l
l l
l
l l
l
l
l
l
l
l
l
ll l l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l ll
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
ll l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l l l
l
l
l l
l
l
l
l
l
l
l
l
l
ll l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l l l
l
l
l ll
l
l
l
l
l l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
lllll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
ll l
l
l
l
l l
l
l
l
ll
l
l
l
l l
l
l l
lll ll
l l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l l
l l
l
l
l
l
l l
l
l ll
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
ll l
l
l
l
ll
l
l
l
l
l l l
l
l l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l ll
l
l l l
l l
l
l
l l l l
ll
l
l l
l
l ll
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
ll
l
l
l l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
ll
l l
l l l l
l
l
l
l
l
l
l
l
l
l
ll l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll l
l
l l
l
l
l
l
l
l
l
l
l
l l ll
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l l
l
ll
l
l l
l l l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
ll l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l ll l l
ll
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
ll l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l l ll
l
l
l
l
l
l
l ll
l
l l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
ll
l
l
l
l l
ll l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l
l l
l
l
ll l
l l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l ll l
l
l l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l l l
l
l
ll
l l
l
ll l
l l l
l l
l
l
l
l l
l
l
ll
lllll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l ll
l ll
l l
l
l
l
l
ll l l l l
l
l
l l
l
l
l ll l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
ll l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l l
l l
l
l
l
l
l
l l l
l
l l l
l
ll
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
ll
l
l
l
lll
l
l
l ll
l
l
l
l
l
l
l l
l
l
l l
ll
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll ll l l
l
ll
l
l
l
l
l
l l
l l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l l
l l
l
l
l
l l l
l
l
l l
l
l l
l l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
ll
l ll
l
l
l
l
l
l
l
l
l
l
l l ll
l
l
ll l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l l
l l
l l
l
l l l
l l
l
l
l l l
l
l
l l l
l
l
l
l
l
l l l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l l l
l l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l l
l
ll l
l
l l l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l ll
l
l l l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll l
l
l
ll
l
l l
l
l l
l
l l
l l l
l l
l
l
l l
l
l
l
ll
l l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l
l l ll
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l l l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l l
l llll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l l l
l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l l
l
l
l
ll l
l
l
l l l
l
l
l
l
l
l
l
l l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
ll
l
l l l ll
l l l
l
l
l
l l
l
l l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l l
l
ll l
l l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l l l
l l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l l ll l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l ll
l
l
l
l
l l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
lll
l
l l
l
l
l
l
l l l l l
ll l
l
l
l
l
l
l ll l
l l
l
l l
ll
l l l
l
l
l
l
l
l
l
l
l
l
l ll
l l
l
l
l l
l
l
l
l
l l
l l
l
l
l l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
ll l
ll
l
l
l
l
l
l
l
l
l
l
l
l l l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l l l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l l
ll
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l l l
l
l l
l
l
l
l
l
l
l
l
l l l l
l l l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l l
l l
l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l ll l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l l ll
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l l l
l
l
l
ll l
ll l
l
l l l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l ll
l
l
l
l l
ll l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l l l l
l
l l
l
l l
l
l l
l l
l
l
l
l
l l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l ll l
l l
l
l
l
l
l
l ll
l
l
l l
l
l ll l
l
ll l
l l
l l
ll
l
l
l
ll ll
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l l
l
l l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
ll l
l
l
l l
l
l
l
l
l
l
l
l
l
−5 0 5 10
−5 0 5 10
HML
linear extrapolation
Market
−3 −2 −1 0 1 2 3
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
ll l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l l
l
l
ll
l
l
l
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll l
ll
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l l
l
l l
l l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
ll
l ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l ll
l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
ll
l l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
ll
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
ll
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
ll
l l
l
l
l
l
l
l ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
llll
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l
l l
l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
lll
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
ll
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
−4 −3 −2 −1 0 1 2
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l l
l
l l
l l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
ll
l
l
l l
l
l
l
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
ll
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll l
l l
l
l
l
l
l
l
l
l
l l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
lll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
ll
l l
l
l ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
ll ll l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
ll l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
ll l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
ll
l
l
l
l
l l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l l
l l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l ll
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
ll l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l
l l
l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
ll
l
l l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l lll
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
−3 −2 −1 0 1 2 3
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l l
l
l l
l
l l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
ll
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll l
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
ll
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
ll
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
ll l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
SMB
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l l
l
l l
l
l l
l
l
ll
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
lll
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
ll
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l ll l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l l
l l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
−4 −3 −2 −1 0 1 2
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l l
l
l
l l
l l
l l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l ll
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l
l l l
l
l
l
l
l l
l l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
ll
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l l
l
ll
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll l
l
l
l
l
l
l
l
l ll
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
llll
l
l
l
l
l
l l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l ll
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
ll
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll ll
l
l l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l ll
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
ll l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
ll
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
ll
l
l
l
ll
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l l
l
ll
l
l ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l lll
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l l
ll l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l ll
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
lll l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l lll
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l l
l
lll
l l
l
l
l
ll
l
l l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l l
l
ll
l
l l
l
l l
l
l
l
l
l
l
l
l l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l ll l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l l
l
l ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
ll l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
ll
l
l l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
ll
l
l ll
l
l ll
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l l
l
l
l l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l l l
l
l
l
l l
l l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l l
l l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l ll
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l l
l l l
l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l l
l
l
l l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll l
l
l
l
l
l
l
l
l l l
l
l
l
ll
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
ll l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l lll
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
ll
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
ll
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l ll
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l l
l
l
l
l l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
ll l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
ll l
l
l
l
l
l l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l l
l
l
l
l l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l l
l
ll
l
ll l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
ll
l
l l
l
l
l
l
l
l
l
l
l ll l l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l l
ll l
l
l
l
l
ll
l l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l l l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll l l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
ll
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll ll
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l ll
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l l
l
l l l
l l
l
l
l
l l
l
l l
l
l
l
l
lll
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l l
l
l
l
l
l l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
ll
l
l
lll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l l
l
ll
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l
ll l
l
l l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
ll
l l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l ll
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
lll
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l l
l
l l l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l l
l l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l l
l
ll l
l
l l l
l
l l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll l
l
l
l
ll
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l l l
l
l
l l
l
l l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l l
l l
l
l
l
l
l
l
l
l
l
l
l
l l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ll
l
l
l
l
l
l
l
l
l
l
l
l
l
l
−2 0 2 4
−2 0 2 4
HML
smoothing splines extrapolation
Figure 17: Original and simulated samples for the GARCH(1,1) residuals
pseudo-observations from a uniform distribution and converted them back to observations using
our original 20 observations sample. Following our example, we can now obtain a large sample of
residuals (l = 104 here) that we show in the center of

375. gure 17 along with the original residuals
on the left-hand side. As we can observe, the linear interpolation is not robust to outliers and
poorly sampled empirical distributions. This is why we improve Meucci's algorithm by simply
using smoothing splines for the extrapolation and show this result on the right-hand side of

376. gure
17. With the model for the dynamics, we can now generate a large sample of factors returns
with our modeled distributions for t + 1, that is
byt+1 =
0
BB
@
by1;1 by1;L
...
...
...
bys
l;1 bys
l;L
1
CC
A; (76)

377. The scenario-based approach 57
with
byt+1
;i = bi + bi;t+1bzs
;i;
b2
i;t+1 = b!i + bi (ri;t bi)2 + b

378. ib2
i;t; (77)
for all i 2 f1; ;Lg. To close the loop, we

379. nally use the linear model described in subsections
1.4 to obtain a sample of arbitrary size l from the modeled distribution of the N-dimensional
vector of risk-factors at time t + 1, that is
bx
t+1 =
0
BB@
bx1;1 bx1;N
...
...
...
bxl;1 bxl;N
1
CCA
=
ba
+ bB
byt+1
+ bE
t+1
; (78)
where bE
t+1
is a l N matrix withbE
t+1
;i simulated as a Gaussian with a variance equal to
dV ar [i] from the linear factor model (20). We are now ready to use the entropy pooling to bend
probabilities according to market views and show some possible applications in the next two
sections.
4.6 Numerical example : portfolio stress testing
4.6.1 Measures of market risk
Since the beginning of modern portfolio theory in 1952 with Markovitz, the variance has been
a widely accepted and used measure of risk. While it is easy to understand, it has the major
drawback of being symmetric: indeed

380. nancial institutions are usually more concerned about
large losses than about large gains. It is only in 1996 that the amendment to the Basel Accord
to incorporate market risks [55] introduced the Value-at-Risk (V aR) as a new industry-wide
standard. For a security whose return over the next investment period is represented as the
random variable r, the V aR is de

381. ned mathematically as the -quantile of the loss distribution,
that is
V aR (r) = inf fx 2 R : P (r x) g : (79)
It represents the minimal loss in the 1 percent worst cases and one choses typically close
to 1. There exists various parametric estimators for the V aR, and it can also be computed
directly using past returns or Monte-Carlo simulations. However, it has the drawback of hiding

382. 58 Views Integration in Quantitative Portfolio Allocation
risk behind a con

383. dence interval, as the actual loss, by de

384. nition beyond the V aR, may be in
fact much larger than the V aR. Furthermore, it has been stipulated (for instance in [46]) that a
coherent risk measure on the space of real-valued random variables should ful

385. ll the following
properties:
1. Monotonicity: for two random variables x y, then (x) (y).
2. Sub-additivity: for two random variables x and y, then (x + y) (x) + (y).
3. Positive homogeneity: for a random variable x and a scalar 0, then (x) = (x).
4. Translation invariance: for a random variable x and a scalar 2 R, then (+x) = +(x).
As it lacks the sub-additivity property, the V aR is not a coherent risk measure in the sense
that diversi

386. cation does not reduce risk in general. Furthermore, the empirical quantile function
to compute the V aR using scenarios (historical or Monte-Carlo) is often non-smooth and non-convex.
Thus it yields many problems when one wants to optimize a portfolio using this risk
measure, as many local optimizers can be encountered (see [21] for instance). An alternative
measure which does not suer from these pitfalls is the conditional Value-at-Risk (CV aR) or
expected shortfall (ES). Mathematically, it is the expected losses in the 1 worst cases, that
is
CV aR (r) =
E[r jr V aR (r) ]
1
=
1
1
1
V aR
(r) d
; (80)
where the second line emphasizes the fact that the CV aR represents the expected loss given
that the V aR is crossed. We present a comparison between the V aR and the CV aR for the
Gaussian and student distributions in

387. gure 18, and we observe that the CV aR is signi

388. cantly
higher and that this dierence increases with the fatness of the distribution's tails. As for the
V aR, the CV aR can be computed from parametric estimators or directly using the historical
returns or Monte-Carlo simulations, but it is a coherent and convex risk measure.

389. The scenario-based approach 59
−4 −2 0 2 4
0.0 0.1 0.2 0.3 0.4
x
Density(x)
Gaussian
Gaussian VaR
Gaussian CVaR
Student t with df=5
Student t VaR
Student t CVaR
2 5 10 20 50 100 200 500
0.5 1.0 2.0 5.0 10.0
Degrees of freedom
Risk
Gaussian −VaR
Gaussian −CVaR
Gaussian VaR−CVaR
Student t −VaR
Student t −CVaR
Student t VaR−CVaR
Figure 18: Gaussian and student V aR and CV aR, as well as the dierence between the two risk
measures with respect to the degrees of freedom for the Student t.
4.6.2 Stress testing
We now use the market model described in subsection 4.5 to obtain a large sample of l = 105
joint realizations
bx
t+1
i; =
bxt+1
i;1 ; ; bxt+1
i;n ; bxt+1
i;MKT ; bxt+1
i;SMB; bxt+1
i;HML
; (81)
for i 2 [1; ; l] from the estimated distribution of returns over the next period with probabilities
initially set as pi;t+1 = 1=l 8i 2 [1; ; l]. For the market portfolio with wm;t, one can then
compute[V aR (rp;t+1 jIt;Jt ) as the empirical (potentially weighted) quantile function, and
CV aR (rp;t+1 jIt;Jt ) =
X
j2C
m;tbx
pj;t+1w
t+1
j; ;
where C stands for indices for which the portfolio loss is larger than the value-at-risk, that is
C
n
j : w
t+1
j; [V aR (rp;t+1 jIt;Jt )
m;tbx
o
:
In the

390. rst row of table 7, we show the expected return, the value-at-risk and the expected
shortfall for the market portfolio, estimated directly using our simulated model. One may

391. rst
observe by annualizing the weekly value that the expected return of the portfolio is 5:65%, less
than half the 14:89% estimated using historical returns from December 2009 until December 2011
in the Black-Litterman model. In fact, from the original range [6:15%; 45%] for the securities
expected return, our sampled distribution yields expected annual returns between 8:83% and
29:90%. To address this issue, we input a

392. rst view constraining the weekly expected return
of the securities at their historical expected value. We observe in the second row of table 7,

393. 60 Views Integration in Quantitative Portfolio Allocation
bE
[rp;t+1 jIt;Jt ] [V aR0:95 (rp;t+1 jIt;Jt ) CV aR0:95 (rp;t+1 jIt;Jt )
No view 0:11% 5:01% 7:44%
Factor's

394. rst moment 0:25% 4:52% 6:98%
Stressed factors 0:25% 8:54% 10:80%
Table 7: Market portfolio expected performance and risk under views speci

395. cations
that the expected return of our portfolio, at 13:30%, is then much closer to the historically
estimated value using data from December 2009 until December 2011. In fact, we can compute
the distance sum20
j=1 jbj ej j with bj the historical estimator from January 1999 to December
2011 and ej our new estimator, once computed with pi;t+1 = 1=l 8i 2 [1; ; l] and then with
pooled probabilities obtained by constraining the

396. rst moment of factors. We observe that
the distance between the historical estimator of the

397. rst moment and the estimator from our
model decreases as expected by the view from 2:87 102 to 4:98 108. Constraining the

398. rst
moment by being more optimistic than our original model also induces an eect on risk, as it
can be observed that both [V aR0:95 (rp;t+1 jIt;Jt ) and CV aR0:95 (rp;t+1 jIt;Jt ) decreases. We
recall that a desirable feature of a view-integration framework is the possibility of stress-testing
portfolios, that is of performing various risk estimations under some pessimistic assumptions.
There are several possible speci

399. cations for stressed-markets, and we choose here to stress our
portfolio by increasing the volatility. Thus we constraint the volatility of the factors to be twice
their historically realized volatility, while keeping the

400. rst moment of the securities constrained.
In the third row of table 7, we

401. nally observe that the expected return of the portfolio hasn't
changed, but that the risk has increased as expected. Such application is handy when one wants
to understand how his portfolio may react in case of market evolving in a direction one couldn't
have inferred from past or present publicly available information.
4.7 Numerical example: mean-variance, market equilibrium and relative entropy
In this subsection, we attempt to reconcile the concepts of mean-variance allocation56 and market
equilibrium along with our
exible model and the entropy pooling framework. As we show on the
left-hand side of

402. gure 19, mean-variance portfolios obtained directecly from the sampled market
model suer from the same concentration problems we exposed in subsection (3.1), although to
a lesser extent. To correct this we implement our

403. rst view to contraint the

404. rst moment for the
56We keep the mean-variance allocation, given there exists many alternative schemes. The mean-CV aR, that
we describe in details in appendix (C), and most alternative schemes are not as straightforward to interpret in
terms of the Taylor developpement of the utility as the mean-variance. Furthermore, an empirical study (see [54])
showed that real traders are mean-variance on average.

405. Conclusion 61
individual securities at their equilibrium expected value, de

406. ning a CAPM probability measure
ep
CAPM. As in BL, it regularizes the problem as we show in the center of

407. gure 19. Furthermore,
we show with the vertical black line that we fall again on the market portfolio when using the
market implied risk-aversion. We choose to observe the eect of a simple view by doubling the
market implied expected return of OXY. Thus, we

408. nd ep
view argmin
ep
2C
n
bD
KL (ep;ep
o
,
CAPM)
where ep
2 C is a measure of probability (that is
P105
i=1 pi = 1 and pi 0 for all i 2
1; ; 105
)
such that ep
bx
t+1
;OXY = 0:2%. We show in the right-hand side of

409. gure 19 the resulting mean-variance
ecient frontier, where we observe that OXY (in light blue) is now held for most
risk-aversions.
0 2 4 6 8 10
0 20 40 60 80 100
No view
Weight %
Risk aversion
0 2 4 6 8 10
0 20 40 60 80 100
CAPM's view
Weight %
Risk aversion
0 2 4 6 8 10
0 20 40 60 80 100
CAPM bullish on OXY
Weight %
Risk aversion
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
l
ORCL
MSFT
KO
XOM
GE
IBM
PEP
AAPL
PG
ABT
PFE
JNJ
OXY
WFC
MCD
WMT
INTC
CSCO
QCOM
AMZN
Figure 19: Mean-variance allocations in the
exible market model.
5 Conclusion
Empirical views are a key ingredient to the good modeling and validation of view integration
techniques into actual portfolio allocation schemes. As often in

410. nance, the assumptions one
has to make in order to develop a sound theoretical framework, as the Black-Litterman model
and Meucci's entropy pooling, are constraining, sometimes simplifying too drastically real-world
situations and behaviors. It becomes therefore crucial to understand and assess the unavoidable
discrepancies between actual facts (e.g. trading habits) and model assumptions. While Meucci's
practitioner approach is appealing by its
exibility and ecient implementation, it still suers
from the theoretical drawback that many views one can think of are actually inconsistent, and
this problem is linked to the relative entropy rather than the market model. In fact, this issue
can only be adressed by either modifying these views or minizing a divergence devoted to non-equilibrium
systems (e.g. Tsallis's, see subsection (1.5)).

411. 62 Views Integration in Quantitative Portfolio Allocation
In what follows we focus on Black-Litterman's extension of the mean-variance allocation. In
simple words, the classical Black-Litterman is optimal under the same market assumptions as
the mean-variance's, that is essentially a market at equilibrium characterized by the

412. rst two
moments57. As expected market views should also ful

413. ll an associated assumption of Gaussianity.
This comes at no surprise as market views, if realized, turn into actual observations, that is a
realized one-day view on the return of an asset becomes the actual one-day return of the asset
if it is realized in the prescribed one-day horizon. Hence within a given theoretical frame, one
has to require views on returns to exhibit similar statistical and dynamical properties as those
assumed for the returns. This requirement is indeed mandatory for the sake of coherence as
Gaussian markets may not preserve normality under non-Gaussian views. Obviously, the same
line of reasoning applies to views on other quantities constrained by the model to have peculiar
statistical and dynamical features e.g. volatility short-memory, negligible excess-kurtosis and
risk-skewness, all of which are implicit in Black-Litterman.
We argue that limit orders58 can be studied as real-world market views by considering the relative
dierence between the limit price and the bid/ask, that is
b;t =
pb;t pl
pb;t
and a;t =
pl pa;t
pa;t
;
where t is the time at which the order is placed and we de

414. ne the (approximative) price of the
security as the midprice (pa;t + pb;t) =2. We can give a simple market view by considering for
instance an investor who wishes to sell a stock at pl pa;t within a period of time t, which is
the expiration time of the limit order. As the utility of not being matched is zero, the limit order
can be seen as a view on the future price pl = (pa;t+t + pb;t+t) =2. This interpretation has an
obvious limitation: as for analysts who give recommendation within a given time horizon, the
limit order represents a view that can be ful

415. lled long before its horizon. Furthermore, many
limit orders are cancelled manually by investors before their expiration date. However, it is still
a proxy for real-world market view to start with. In [62, 14, 56] for instance, authors observe
that the distribution of views exhibits fat tails with remarkable regularity, suggesting that the
distribution of actual views may depart strongly from the Gaussian assumption implied in the
mean-variance and Black-Litterman models, as do the

416. nancial markets.
This however does not imply that such models are (always) inappropriate, non optimal, or
even give an unrealistic description of portfolio allocation practices followed by actual investors.
57Relaxation of this hypothesis has been proposed in the form of a three moments CAPM, described for instance
in [44]
58A limit orders are orders to buy or sell a security at a speci

417. c price (or better), and within a speci

418. c time
horizon, as opposed to market orders which are orders to buy or sell as soon as possible at any price.

419. REFERENCES 63
It merely asserts that, assumptions being violated, one cannot ensure that ecient portfolios
provide the best investment opportunities for the future. In fact, it has been shown in [54] that
real traders are mean-variance on average, taking transaction costs into account. Furthermore
in [39], authors considered a generae utility function expanded to fourth order, showing that
the resulting allocations are not necessarily dierent from the mean-variance portfolios, except
for very high risk aversions in the absence of short selling and of a risk-free asset. In practice,
we believe that the impact of non-Gaussian market views in a mean-variance framework is of
utmost importance and we tried to give an example in subsection (19). We think that the
subject deserves to be the focus of further theoretical and empirical research in order to reconcile
the non-Gaussianity consensus about

420. nancial markets and views along with the mean-variance
allocation which emerges from the collective behavior of real traders.
6 Acknowledgments
I would like to express my gratitude to all those who gave me the possibility to complete this
thesis. My

421. rst debt of gratitude must go to Dr. David Morton de Lachapelle to whom theWe
I used along the document is mainly dedicated. His patience, thoughtful advices, constant men-toring
and remarkable ability to see the big picture have been my biggest source of inspiration
and motivation since I started to work with him. I also wish to thank all Swissquote's QAM
team members for the six months I spent with them: Damien Ackerer for daily fruitful discus-sions
on many topics of

422. nance, economics, statistics, mathematics, physics and life in general,
Florent Gallien for his absolute mastery of mathematical optimization and dedicated backtesting
framework and

423. nally Dr. Serge Kassibrakis for hiring me and being an understanding leader
with researchers working in an industrial environment. Finally, I wish to thank the Prof. Paolo
De Los Rios for keeping an open mind and interdisciplinary vision of physics: trusting David to
mentor me and giving us complete freedom in a subject he did not fully masterize was an act of
faith that I believe has proven successful.
References
[1] Adda, J., and Cooper, R. W. Dynamic Economics. MIT Press, 2003.
[2] Ali, S. M., and Silvey, S. D. A General Class of Coecients of Divergence of One Dis-tribution
from Another. Journal of the Royal Statistical Society, Series B (Methodological),
Vol. 28, Issue 1 (1966), pp. 131-142 (1966).

424. 64 Views Integration in Quantitative Portfolio Allocation
[3] Avellaneda, M. Minimum-relative-entropy calibration of asset pricing models. Interna-
tional Journal of Theoretical and Applied Finance 1: 447-472 (1998).
[4] Avellaneda, M., Friedman, C. A., Holmes, R., and Samperi, D. J. Calibrating
volatility surfaces via relative-entropy minimization. Journal of

425. nancial and quantitative
analysis (1996).
[5] Bacon, C. R. Practical portfolio performance measurement and attribution, 2nd Edition.
John Wiley Sons, 2008.
[6] Barber, B., Lehavy, Reuven adn McNichols, M., and Trueman, B. Can investors
pro

426. t from the prophets? Security analyst recommendations and stock returns. The Journal
of Finance, Vol. 56, No. 2 (2001).
[7] Barber, B., Lehavy, Reuven adn McNichols, M., and Trueman, B. Prophets and
losses: reassessing the returns to analysts' stock recommendations.
[8] Barber, B., Lehavy, Reuven adn McNichols, M., and Trueman, B. Buys, Holds,
and Sells: the distribution of investment banks' stock ratings and the implications for the
pro

427. tability of analysts' recommendations. Journal of Accounting and Economics, Vol. 41:
87-117 (2006).
[9] Best, M., and Grauer, R. On the sensitivity of mean-variance-ecient portfolios to
changes in asset means: some analytical and comptational results. The Review of Financial
Studies, Vol.4, No. 2: 315-342 (1991).
[10] Black, F., and Litterman, R. Global Portfolio Optimization. Fixed Income Research,
Goldman, Sachs Company, September (1990).
[11] Black, F., and Litterman, R. Asset Allocation: Combining Investors Views withMarket
Equilibrium. Financial Analysts Journal, pp. 28-43, September/October 1992 (1992).
[12] Bollerslev, T. Generalized Autoregressive Conditional Heteroskedasticity. Journal of
Econometrics, 31:307-327 (1986).
[13] Bollerslev, T., and Wooldridge, J. Quasi-Maximum Likelihood Estimation and Infer-ence
in Dynamic Models with Time-Varying Covariance. Econometric Reviews 11, 143-172
(1992).
[14] Bouchaud, Jean-Philippe and Mezard, Marc and Potters, Marc. Statistical
Properties of Stock Order Books: Empirical Results and Models. Quantitative Finance,
Vol. 2: 251-256 .

428. REFERENCES 65
[15] Buchen, P. W., and Kelly, M. The Maximum Entropy Distribution of an Asset Inferred
from Option Prices. Journal of

429. nancial and quantitative analysis (1996).
[16] Cheung, W. Generalised Factor View Blending: Augmented Black-Litterman in Non-
Normal Financial Markets with Non-Linear Instruments. SSRN eLibrary (2009).
[17] Cheung, W. The Black-Litterman Model Explained. SSRN eLibrary (2009).
[18] Cheung, W. Transparent Augmented Black-Litterman Allocation: Simple and Uni

430. ed
Framework for Strategy Combination, Factor Mimicking, Hedging, and Stock-Speci

431. c Al-phas.
SSRN eLibrary (2009).
[19] Cheung, W. The intrinsic logic of the augmented Black-Litterman model. SSRN eLibrary
(2010).
[20] Cheung, W. The Augmented Black-LittermanModel: A Ranking-Free Approach to Factor-
Based Portfolio Construction and Beyond. SSRN eLibrary (2011).
[21] Cornuejols, G., and Tutuncu, R. Optimization Methods in Finance. Cambridge Uni-versity
Press, 2007.
[22] Csiszar, I. Eine informationstheoretische Ungleichung und ihre Anwendung auf den Beweis
der Ergodizitat von Markoschen Ketten. Magyar. Tud. Akad. Mat. Kutato Int. Kozl 8: pp.
85-108 (1963).
[23] Dey, S., and Juneja, S. Entropy Approach to Incorporate Fat Tailed Constraints in
Financial Models. SSRN eLibrary (2010).
[24] DiCiccio, T. J., and Efron, B. Bootstrap Con

432. dence Intervals. Statistical Science, Vol.
11: 189-228 (1996).
[25] Efron, B. Better Bootstrap Con

433. dence Intervals. Journal of the American Statistical
Association, Vol. 82, No. 397: 171-185 (1987).
[26] Elton, E. J., Gruber, M. J., Brown, S. J., and Goetzmann, W. N. Modern Portfolio
Theory and Investment Analysis, 7th Edition. John Wiley Sons, 2007.
[27] Fama, E. F. The behavior of stock-market prices. The Journal of Business, Vol. 38, No.
1: 34-105 (1965).
[28] Fama, E. F., and French, K. R. The Cross-Section of Expected Stock Returns. The
Journal of Finance 47 (2): 427-465 (1992).

434. 66 Views Integration in Quantitative Portfolio Allocation
[29] Fama, E. F., and French, K. R. Common Risk Factors in the Returns on Stocks and
Bonds. Journal of Financial Economics 33 (1): 3-56 (1993).
[30] Finnerty, J. E. Insiders and Market Eciency. The Journal of Finance, Vol. 31, No. 4:
1141-1148 (1976).
[31] Fisher, I. The theory of interest. New York: The Macmillan Co., 1930.
[32] Genest, C., and Rivest, L.-P. Statistical inference procedures for bivariate Archimedean
copulas. Journal of the American Statistical Association, 88, 1034-1043 (1993).
[33] Grinold, R. C., and Kahn, R. N. Active Portfolio Management: A Quantitative Ap-
proach for Producing Superior Returns and Controlling Risk, 2nd Edition. McGraw-Hill,
1999.
[34] Idzorek, T. M. A step-by-step guide to the Black-Litterman model: Incorporating user-speci

435. ed con

436. dence levels.
[35] Jaffe, J. F. Special Information and Insider Trading. The Journal of Business, Vol. 47,
No. 3: 410-428 (1974).
[36] Jegadeesh, N., Kim, J., D. Krische, S., and Lee, C. M. Analyzing the analysts: when
do recommendations add value? The Journal of Finance, Vol. 59, No. 2 (2004).
[37] Jeng, L. A., Zeckhauser, R. J., and Metrick, A. Estimating the returns to insider
trading: a performance-evaluation perspective. The Review of Economics and Statistics,
453-471 (2003).
[38] Joe, H., and Xu, J. The estimation method of inference function for margins for mul-tivariate
models. Technical Report no.166, University of British Columbia, Department of
Statistics (1996).
[39] Jondeau, Eric and Rockinger, Michael. How Higher Moments Aect the Allocation
of Assets. Finance Letters, Vol. 1, No. 2 (2003).
[40] Kapur, J. Maximum Entropy Models in Science and Engineering. New Age International
Publishers, Wiley series in Telecommunications, 2009, 2009.
[41] Lakonishok, J., and Lee, I. Are insider trades informative? Review of Financial Studies,
Vol. 14, No. 1 (2001).
[42] Ljungqvist, A., Malloy, C. J., and Marston, F. C. Rewriting History. AFA 2007
Chicago Meetings Paper (2008).

437. REFERENCES 67
[43] Lorie, J. H., and Niederhoffer, V. Predictive and Statistical Properties of Insider
Trading. Journal of Law and Economics, Vol. 11, No. 1: 35-53 (1968).
[44] Maillet, Bertrand and Jurczenko, Emmanuel. The Three-moment CAPM: Theoret-
ical Foundations and an Asset Pricing Models Comparison in a Uni

438. ed Framework. John
Wiley and Sons, 2001, pp. 239{273.
[45] Markowitz, H. Portfolio Selection. The Journal of Finance, Vol. 7, no. 1, pp. 77-91,
March 1952 (1952).
[46] McNeil, A. J., Frey, R., and Embrechts, P. Quantitative Risk Management: Con-
cepts, Techniques, and Tools. Princeton University Press, 2005.
[47] Meucci, A. Fully Flexible Views: Theory and Practice. Risk, Vol. 21, No. 10, pp. 97-102,
October 2008 (2008).
[48] Meucci, A. The Black-Litterman Approach: Original Model and Extensions. SSRN eLi-
brary (2008).
[49] Meucci, A. Historical Scenarios with Fully Flexible Probabilities. SSRN eLibrary (2010).
[50] Meucci, A. A New Breed of Copulas for Risk and Portfolio Management. Risk, Vol. 24,
No. 9, pp. 122-126 (2011).
[51] Meucci, A. Mixing Probabilities, Priors and Kernels via Entropy Pooling. GARP Risk
Professional, pp. 32-36, December 2011 (2011).
[52] Meucci, A. Eective Number of Scenarios in Fully Flexible Probabilities. GARP Risk
Professional, pp. 32-35, February 2012 (2012).
[53] Morton de Lachapelle, D. Modern Portfolio Theory Revisited : from Real Traders to
New Methods. PhD thesis, Doctoral school Physics, 2012.
[54] Morton de Lachapelle, David and Challet, Damien. Turnover, account value and
diversi

439. cation of real traders: evidence of collective portfolio optimizing behavior. New
Journal of Physics, Vol. 12 .
[55] on Banking Supervision, B. C. Amendment to the capital accord to incorporate market
risks.
[56] Potters, Marc and Bouchaud, Jean-Philippe. More statistical properties of order
books and price impact. Physica A: Statistical Mechanics and its Applications, Vol .324:
133-140 .

440. 68 Views Integration in Quantitative Portfolio Allocation
[57] Rockafellar, R., and Uryasev, S. Optimization of Conditional Value-at-Risk. The
Journal of Risk. Vol. 2, No. 3, pp. 21-41 (2000).
[58] Seyhun, H. N. Insiders' pro

441. ts, costs of trading, and market eciency. Journal of Financial
Economics, No. 16: 189-212 (1986).
[59] Vitali, S., Glattfelder, J. B., and Battiston, S. The network of global corporate
control. PLoS ONE 6(10): e25995. doi:10.1371/journal.pone.0025995 (2011).
[60] Walters, J. The factor tau in the Black-Litterman model. SSRN eLibrary (2010).
[61] Xiao, Y., and Valdez, E. A. A Black-Litterman asset allocation model under elliptical
distributions. SSRN eLibrary (2010).
[62] Zovko, Ilija I. and Farmer, J. Doyne. The power of patience: A behavioral regularity
in limit order placement. Quantitative Finance, Vol. 2: 387-392 .
A The Fama and French factors
The description in this appendix is heavily inspired by that one can found on French's website
http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/. On his website, French provides port-folios
formed on size and book-to-market, as well as the factors we used in the document, which
are constructed starting with those portfolios. The portfolios, which are constructed at the end
of each June, are the intersections of 2 portfolios formed on size (ME, market equity or market
capitalization) and 3 portfolios formed on the ratio of book equity to market equity (BE/ME).
The portfolios for July of year t to June of t+1 include all NYSE, AMEX, and NASDAQ stocks
for which they have market equity data for December of t1 and June of t, and (positive) book
equity data for t 1. The size breakpoint for year t is the median NYSE market equity at the
end of June of year t. Book-to-market for June of year t is the book equity for the last

442. scal year
end in t 1 divided by market equity for December of t 1. The book-to-market breakpoints
are the 30th and 70th NYSE percentiles. The Fama and French factors are constructed using
those 6 capital weighted portfolios formed on size and book-to-market. SMB (Small Minus Big)
is the average return on the three small portfolios minus the average return on the three big
portfolios, while HML (High Minus Low) is the average return on the two value portfolios minus

443. Jensen-Shannon's divergence minimization 69
the average return on the two growth portfolios, that is
SMB =
1
3
(Small Value + Small Neutral + Small Growth)
1
3
(Big Value + Big Neutral + Big Growth) ;
HML =
1
2
(Small Value + Big Value)
1
2
(Small Growth + Big Growth) :
Finally, the return on the market is the capital weighted return on all NYSE, AMEX, and
NASDAQ stocks.
B Jensen-Shannon’s divergence minimization
In this appendix, we extend Meucci's results by providing the dual formulation of a symmetric
form of relative entropy. The Jensen-Shannon's divergence is de

444. ned as:
DJS
e F; FxjI
= DKL
e F;
FxjI + e F
2
!
+ DKL
FxjI ;
FxjI + e F
2
!
Also known as information radius or total divergence to the average, it has de

445. ned lower and
upper bounds and its square root is a metric. We summarize the views using the formalism
described in subsection 4.3 as K1 equality constraints in the K1 l matrix and the K1 1
vector and K2 inequality constraints in the K2 l matrix and the K2 1 vector . Then,
we de

446. ne the full-con

447. dence posterior ep
xjI;J as:
ep
xjI;J argmin
ep
2C
ep
log ep
log
pxjI +ep
2
+ p
xjI
log pxjI log
pxjI +ep
2
(82)
C
(
ep
ep
=
(83)
To solve this problem, using p pxjI for notational convenience, we write the Lagrangian
L(ep
;; ) and its

448. rst derivative:
L(ep;; ) =ep
logep
log
p +ep
2
+ p
logp log
p +ep
2
+ (ep
) + ( ep
)
@L(ep
;; )
@ep
= logep
log
p +ep
2
+ +

449. 70 Views Integration in Quantitative Portfolio Allocation
Setting the gradient to zero yields the Bose-Einstein statistics for ep
(; ) that we presented in
subsection 4.1 and the dual function G (; ) L(ep
(; ) ;; ):
ep
(; ) = p

450. e
2 e
G (; ) = p log
2 e
Where we used

451. for the Hadamard product59, the exponential and logarithm are taken element
wise, 2 is a vector of ones (same size as p) and with a vector = + and =
+ . In the dual problem, we optimize over 0 and , that is K = K1 +K2 variables
for our K views, and it is straightforward to compute analytically the gradient as
@G (; )
@
= ep
(; ) ;
@G (; )
@
= ep
(; ) :
Finally, as the dual of a convex optimization problem is concave, one can simply use a quasi-
Newton or conjugate gradient based method for the maximization (as opposed to the minization
in the primal space) which allows us to

452. nally obtain the posterior probabilities:
(; ) argmax
0;
G (; ) =)ep
xjI;J = p

453. e
+
2 e
+
C Mean-CV aR optimization
In this thesis, we only considered Markowitz's allocation scheme and its extension by Black-
Litterman. However, many alternative exist, such as the popular the mean-CV aR proposed
by Rockafellar and Uryasev in [57]. They provide a linearization of the CV aR computation,
paving the way to the mean-CV aR allocation scheme. Basically, for a basket of n securities
which return for the next period is a n 1 random vector r, we consider the function
F (w;

454. ) =

455. +
1
1
r2]1;1[n
f (r)
wr

456. +
dr; (84)
59For two matrices A;B 2 R
mn, the Hadamard product H = A

457. B2 R
mn is such that Hi;j = Ai;jBi;j for
all i 2 f1; ;mg and j 2 f1; ; ng.

458. Mean-CV aR optimization 71
where

459. 2 ]0; 1[ is an arbitrary scalar, f (R) the joint density of r = (r1; ; rn), w =
(w1; ;wn) is an arbitrary vector of portfolio weights, and x+ = max (x; 0) 8x 2 R . In
their paper, Rockafellar and Uryasev show that this function is convex in

460. and that for

461. = argmin

462. F (w;

463. ), we have
CV aR (w) = F (w;

464. ) , and
V aR (w) =

465. .
With those de

466. nitions, let us now go back to the problem of the time t portfolio p optimization.
Let us assume that we know work with the market model described in subsection 4.5, which
allowed us to obtain a sample bx
t+1
i =
bxt+1
1;i ; ; bxt+1
n;i
with i 2 [1; ; l] from the estimated
distribution of returns over the next period with probabilities initially set as pi;t+1 = 1=l 8i 2
[1; ; l]. Discretization of the integral of equation (84) on this sample yields
CV aR (wp;tjIt) = min

467. +
1
1
p t+1
w
p;tbx
t+1

468. +
(85)
Then with x+ = argmin
s, we add the slack variables si = 1=l 8i 2 [1; ; l] to obtain
sx0;s0
CV aR (wp;tjIt) = min

469. ;s1;:::;sl2C

470. +
1
1
p t+1s
; (86)
C
8
:
p;tbx
si + w
t+1
i +

471. 0 8i 2 [1; ; l]
si 0 8i 2 [1; ; l]
Pn
i=1 wp
i;t = 1
; (87)
In what follows, we consider the mean-CV aR optimization with a

472. xed target risk tr and we
Parameters

473. wp
1;t wp
n;t s1 sl
Objective 0 b1 bn 0 0
CV aR constraint

474. 0 0 p1
1 pl
1 tr
Constraint on s1 1 bxt+1
1;1 bxt+1
n;1 1 0 0 0
...
...
...
. . .
...
0
. . .
. . .
...
...
... ...
...
. . .
...
...
. . .
. . . 0
...
Constraint on sl 1 bxt+1
1;l bxt+1
n;l 0 0 1 0
Budget constraint 0 1 1 1 0 0 = 1
summarize the optimization problem to obtain the portfolio weights to hold over the next period

475. 72 Views Integration in Quantitative Portfolio Allocation
in the table above, omitting the positivity constraint on the slack variables for convenience. We
observe that this allocation scheme boils down to a linear programming problem on the space
]0; 1[Rn Rl
+. However, it remains slow and impractical when using Monte-Carlo simulations,
as one needs to adds a number of variable equal to the number of scenarios. Moreover, without
hard coded constraints on the portfolio weights, allocations based on linear objective functions
suer from the same concentration problems we exposed in the Black-Litterman chapter.