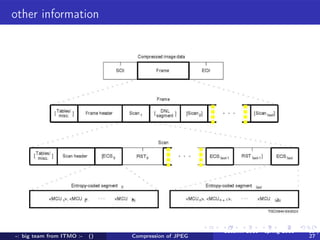
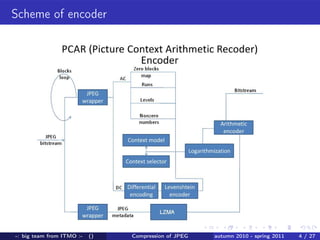
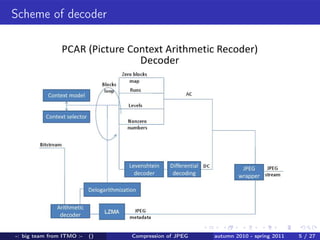
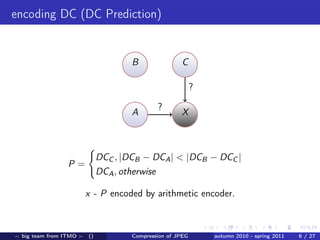
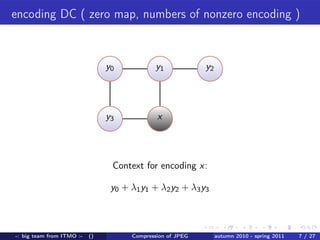
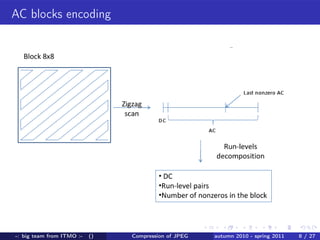
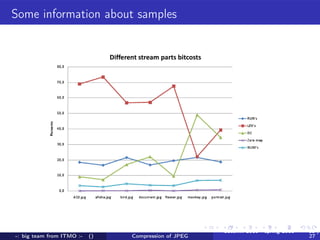
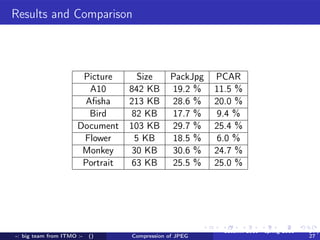
A team from ITMO University worked from autumn 2010 to spring 2011 to improve lossless compression of JPEG files. They developed an encoder and decoder that uses techniques like arithmetic coding to encode DC values, runs of zeros, and AC coefficients in a way that maintains bit-level identical compression and decompression. They tested their algorithm on several images and saw file size reductions of up to 30% compared to the original JPEG files. Maintaining full bit-level compatibility with the JPEG standard presented some challenges around parsing file structures versus a stream-based approach.

1. Improvement of lossless Compression for JPEG files
Irina Bocharova, Kirill Yurkov,
Mikhail Bogdanov, Roman Bolshakov, Alexander Buslaev,
Yuri Konoplev, Anrew Tereskin, Oleg Finkelshteyn
ITMO
autumn 2010 - spring 2011
-: big team from ITMO :- () Compression of JPEG autumn 2010 - spring 2011 1 / 27

2. Agenda
Purpose
Schemes of encoder and decoder
encoding DC
encoding RUN’s and AC
Levenstein encoder
Arithmetic encoder
Results
Problems
-: big team from ITMO :- () Compression of JPEG autumn 2010 - spring 2011 2 / 27

3. Purpose
Realize a recoder of JPEG to reduce bit stream
Requirements: bit-to-bit corrsepondense
-: big team from ITMO :- () Compression of JPEG autumn 2010 - spring 2011 3 / 27

4. Scheme of encoder
-: big team from ITMO :- () Compression of JPEG autumn 2010 - spring 2011 4 / 27

5. Scheme of decoder
-: big team from ITMO :- () Compression of JPEG autumn 2010 - spring 2011 5 / 27

6. encoding DC (DC Prediction)
B C
?
?
A X
DCC , |DCB − DCA | < |DCB − DCC |
P=
DCA , otherwise
x - P encoded by arithmetic encoder.
-: big team from ITMO :- () Compression of JPEG autumn 2010 - spring 2011 6 / 27

7. encoding DC ( zero map, numbers of nonzero encoding )
y0 y1 y2
y3 x
Context for encoding x:
y 0 + λ1 y 1 + λ2 y 2 + λ3 y 3
-: big team from ITMO :- () Compression of JPEG autumn 2010 - spring 2011 7 / 27

8. AC blocks encoding
-: big team from ITMO :- () Compression of JPEG autumn 2010 - spring 2011 8 / 27

9. Runs and levels encoding
We need to encode the pairs: (l0 , r0 ), (l1 , r1 ), . . . , (ln , rn , )
The value n known to encoder. For encoding pair (li , ri ) we construct
two dimensional context:
n
n−i
-: big team from ITMO :- () Compression of JPEG autumn 2010 - spring 2011 9 / 27

10. Arithmetic coding
Arithmetic + Adaptive
model
autumn 2010 - spring 2011 10 /
-: big team from ITMO :- () Compression of JPEG 27

11. Levenstein code
A universal code encoding the non-negative integers
It works so:
code of 0 is "0 and if we want to encode a positive number we do
next:
1 Init the step count var C to 1
2 Write a binary representation of the number without the leading "1"to
the beginning of the code.
3 Let M be the number of bits written in step 2.
4 If M is not 0, increment C, repeat from step 2 with M as the new
number.
5 Write C "1"bits and a "0"to the beginning of the code.
autumn 2010 - spring 2011 11 /
-: big team from ITMO :- () Compression of JPEG 27

12. Some samples
autumn 2010 - spring 2011 12 /
-: big team from ITMO :- () Compression of JPEG 27

13. Some information about samples
autumn 2010 - spring 2011 13 /
-: big team from ITMO :- () Compression of JPEG 27

14. Results and Comparison
Picture Size PackJpg PCAR
A10 842 KB 19.2 % 11.5 %
Afisha 213 KB 28.6 % 20.0 %
Bird 82 KB 17.7 % 9.4 %
Document 103 KB 29.7 % 25.4 %
Flower 5 KB 18.5 % 6.0 %
Monkey 30 KB 30.6 % 24.7 %
Portrait 63 KB 25.5 % 25.0 %
autumn 2010 - spring 2011 14 /
-: big team from ITMO :- () Compression of JPEG 27

15. Problems (bit-to-bit)
We need to read and write JFIF (JPEG) files maintatining bitwise
identity.
Two possible implementation paths:
Full parser: file → internal structrures → file
Pros: very flexible, easy to process once we have the structure
Cons: implementing a writer adhering to the bitwise identity
requirement is difficult. High serialization overhead.
Stream encoder: leaves most of non-interesting metadata as is
(compressing using general-purpose stream methods)
Pros: faster, no serialization code (decoder reuses the jpeg header
parser from encoder), guarantees exactness in metadata
Cons: we lose flexibility, save some redundant information (e.g.
standard Huffman tables)
After several attempts, we settled on the latter solution which works
for an estimate of 95% of JPEG files in the wild (for those we are
unable to process, a diagnostic is provided)
autumn 2010 - spring 2011 15 /
-: big team from ITMO :- () Compression of JPEG 27

16. Problems (Unknown alphabet size)
Starts from alphabet contains one symbol Ω = {ζ},
where ζ is escape symbol
For each new input symbol at+1
1 a ∈ Ω,
τ (a)
encode a with probality distribution p(a) = t+1
2 a∈Ω
/
τ (a)
encode escape symbol with probability distribution p(a) = t+1
encode a with Levenstein code
Ω = Ω ∪ {a}
autumn 2010 - spring 2011 16 /
-: big team from ITMO :- () Compression of JPEG 27

17. Thanks
Questions ?
autumn 2010 - spring 2011 17 /
-: big team from ITMO :- () Compression of JPEG 27

18. References
[Rissanen, J.J.; Langdon, G.G., 1979]
Arithmetic coding
IBM Journal of Research and Development, p: 149-162.
[Levenstein V.I., 1968]
About redundancy and slowdown of difference coding of natural
numbers
Problems of cybernetics, Moscow, Science, p: 173-179.
[Krichevsky, R.E.; Trofimov V.K., 1981]
The Performance of Universal Encoding
IEEE Trans. Information Theory, Vol. IT-27, No. 2, pp. 199–207.
autumn 2010 - spring 2011 18 /
-: big team from ITMO :- () Compression of JPEG 27

19. other information
autumn 2010 - spring 2011 19 /
-: big team from ITMO :- () Compression of JPEG 27