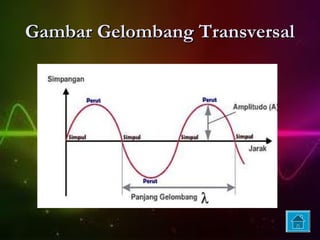
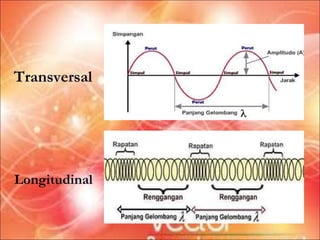
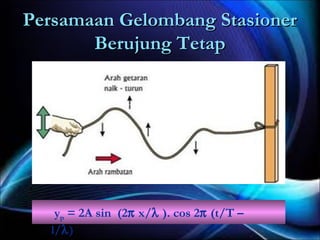
Gelombang adalah getaran yang merambatkan energi, terbagi menjadi gelombang transversal dan longitudinal berdasarkan arah getarnya, serta gelombang elektromagnetik dan mekanik berdasarkan medium perambatannya. Besaran dasar gelombang termasuk periode, frekuensi, panjang gelombang, dan cepat rambat gelombang, dengan sifat-sifat seperti refleksi, refraksi, difraksi, dan interferensi. Persamaan gelombang berjalan dan stasioner dijelaskan dalam konteks amplitudo, frekuensi sudut, dan fase, serta contoh soal yang relevan diberikan.

3. GELOMBANG
 Gelombang adalah getaran yang
merambatkan energi dari satu tempat
ketempat yang lain, baik melalui medium
ataupun tidak.
 Gelombang merupakan salah satu cara
perpindahan energi.

4. JENIS GELOMBANG
Berdasarkan Arah Getarnya:
 Gelombang Transversal
 Gelombang Longitudinal
Berdasarkan Medium Perambatannya:
Gelombang Elektromagnetik
Gelombang Mekanik
Berdasarkan Amplitudonya:
Gelombang Berjalan
Gelombang Stasioner

5. Gelombang Transversal
 Gelombang transversal adalah gelombang
yang memiliki arah getar tegak lurus
terhadap arah rambat gelombang.
 Contoh : gelombang pada tali, gelombang
permukaan air, dan gelombang
elektromagnetik.

6. Gambar Gelombang Transversal

7. Gelombang Longitudinal
 Gelombang longitudinal adalah gelombang
yang memiliki arah getar berimpit terhadap
arah rambat gelombang .
 Contoh : gelombang pada pegas dan
gelombang bunyi.

8. Gambar Gelombang
Longitudinal

9. Gelombang Mekanik
 Gelombang mekanik yaitu gelombang yang
untuk perambatannya diperlukan medium.
 Contoh : gelombang pada tali, gelombang
permukaan air, dan gelombang bunyi.

10. Gelombang Elektromagnetik
Gelombang Elektromagnetik: gelombang
yang perambatannya tidak membutuhkan
medium.
Contoh : gelombang cahaya, gelombang radio,
sinar-X, beta, dan gama.

11. Gelombang Berjalan
 Gelombang berjalan yaitu gelombang yang
amplitudonya tetap pada titik yang dilewatinya.

12. Gambar Gelombang Berjalan
x
v
•P
S

13. Gelombang Stasioner
 Gelombang stasioner yaitu gelombang
yang amplitudonya tidak tetap pada titik
yang dilewatinya.
Gelombang Stasioner merupakan
paduan antara gelombang datang
dengan gelombang pantul (yp=yp1+yp2)

14. Gambar Gelombang Stasioner
L
R
o
S P
L+x x

15. BESARAN DASAR GELOMBANG
 Periode ( T )  satuan sekon ( s )
 Frekuensi ( f )  satuan Hertz ( Hz )
 Panjang gelombang ( λ )  satuan meter ( m )
 Cepat rambat gelombang ( v ) satuan ( m/s )

16. Periode ( T ) & Frekuensi ( f )
 Periode : Waktu yang diperlukan untuk
menempuh satu gelombang (sekon)
 Frekuensi : Banyaknya gelombang yang
terbentuk setiap sekon ( Hz)
 Hubungan antara frekuensi dengan periode :
1 1
f= atau T=
T f

17. Panjang Gelombang
 Panjang gelombang yaitu jarak yang ditempuh
getaran dalam satu periode (satu gelombang
penuh)
 Pada gelombang transversal, satu gelombang
penuh terdiri atas satu bukit dan satu lembah
 Pada gelombang longitudinal, satu gelombang
penuh terdiri atas satu rapatan dan satu
renggangan
λ = v . T atau λ = v/f

18. Transversal
Longitudinal

19. Cepat Rambat Gelombang (v)
 Cepat rambat gelombang adalah jarak
yang ditempuh oleh satu gelombang ( λ )
dalam waktu satu periode ( T ).
λ
 v= atau v=λ.f
T

20. Sifat Gelombang
 Gelombang dapat dipantulkan (refleksi)
 Gelombang dapat dibiaskan (refraksi)
 Gelombang dapat dilenturkan (difraksi)
 Gelombang dapat dipadukan (interferensi)
 Gelombang dapat didispersikan
 Gelombang dapat dipolarisasikan

21. Pemantulan Gelombang
 Bila sebuah gelombang merambat dan
mengenai bidang pembatas yang keras.
 Sudut datang (i) = sudut pantul (r)

22. Pembiasan Gelombang
 Pembiasan yaitu perubahan arah
gelombang saat gelombang masuk ke
medium baru yang mengakibatkan
gelombang bergerak dengan kecepatan
yang berbeda.
 Sin i/sin r = V1/V2 atau sin i/sin r =
n1/n2

23. Difraksi Gelombang
 Pembelokan gelombang yang disebabkan
oleh adanya penghalang berupa celah.

24. Interferensi Gelombang
 Interferensi terjadi pada dua gelombang
koheren, yaitu gelombang yang memiliki
frekuensi dan beda fase yang sama.

25. Dispersi Gelombang
 Dispersi adalah penyebaran atau
penguraian bentuk gelombang apabila
melewati suatu medium tertentu.

26. Polarisasi Gelombang
 Polarisasi yaitu proses pembatasan getaran
vektor yang membentuk suatu gelombang
transversal sehingga menjadi satu arah.

27. Contoh Soal

28. Persamaan Gelombang Berjalan
x
v
•P
S
 Persamaan gelompang di titik P :
 Fase titik P  ϕp = t/T – x/λ
 yp = A sin 2π (t/T – x/λ)
 yp = A sin (2πt/T – 2πx/λ)  jika k = 2π/λ
maka :
 yp = A sin (ω t – kx)

29. Memahami Persamaan Simpangan
Gelombang Berjalan
Simpangan di titik P
Amplitudo
yp = ± A sin (ωt ± kx)
Bilangan gelombang
Frekuensi sudut

30. Persamaan Umum Simpangan
Gelombang Berjalan
 Titik asal ke atas merambat ke kiri
yp = ± A sin (ωt ± kx)
 Titik asal ke bawah merambat ke kanan

31. Frekuensi Sudut & Bilangan
Gelombang
 Frekuensi sudut :
ω = 2 πf atau ω = 2π/T
 Bilangan gelombang :
k = 2 π/ λ

32. Beda Fase
•A •B
 Beda fase antara titik A dan titik B :
∆ϕAB = ϕA - ϕB
dengan ϕ : sudut fase

33. Persamaan Gelombang Stasioner
Berujung Tetap
yp = 2A sin (2π x/λ ). cos 2π (t/T –
l/λ)

34. L
R
o
S P
L+x x
Persamaan di titik P :
yp = 2A cos (2π x/λ ). sin 2π (t/T – l/λ)

35. Amplitudo Gelombang Stasioner
dan Posisi Perut/Simpul, Pada Tali
Berujung Bebas
(x) Posisi perut
kedua
S P S P S P S P S P S P S P S P S P S P S P
 Amplitudo = 2A cos 2πx/λ (x) Posisi simpul
pertama
 Posisi perut (P) : x = (n – 1). ½ λ
 Posisi simpul (S) : x = (2n – 1). ¼λ

36. Contoh Soal
 Seutas kawat digetarkan harmonik sehingga
getaran tersebut merambat ke kanan sepanjang
kawat dengan cepat rambat 10 m/s. Ujung
kawat mula-mula digetarkan ke atas dengan
frekuensi 5 Hz dan amplitude 0,01 m. Jika pada
saat t = 0, simpangannya maksimum.
 Tentukan :
(a) persamaan umum gelombang

37. (b) kecepatan dan percepatan partikel di titik x =
0,25 m pada saat ujung kawat telah bergetar 0,1
sekon.
(c) Sudut fase dan fase gelombang di titik x = 0,25
m pada saat ujung kawat telah bergetar 0,1
sekon.

38. Pembahasan
 Diket :
Cepat rambat v = 10 m/s ; frekuensi f = 5 Hz ;
amplitude A = 0.01 m
(a) Tentukan dahulu ω dan k
ω = 2πf
ω = 2π.5 = 10 π rad/s
cari nilai λ,
λ =v/f =10m/s/5Hz = 2 m
k = 2 π/ λ = 2 π/ 2 = π

39. pada saat t = 0 simpangannya maksimum,
berarti persamaan umum gelombangnya adalah:
yp = + A cos (ω t - kx)
maka persamaan gelombangnya adalah
yp = + 0,01 cos (10 π t - π x),
dengan x dalam meter dan t dalam sekon.

40. (b) Kecepatan dan percepatan partikel
 Kecepatan
vp = dy/dt = 0,01 x 10π (-sin) (10πt - πx)
vp = - 0,1π sin (10π t - π x)
 Percepatan
ap = dv/dt = - 0,1π x 10π cos (10πt - πx)
ap = - π 2 cos (10π t - π x)

41.  Kecepatan di titik x = 0,25 m pada ujung kawat
setelah bergetar 0,1 sekon adalah:
vp = - 0,1 π sin (10 π t - π x)
vp = - 0,1 π sin (10 π.0,1 - π.0,25)
vp = - 0,1 π sin (π - ¼ π)
= - 0,1 π sin (3/4 π)
= - 0,1 π . 1/2√2
vp = - 0,05 √ 2 π m/s

42.  Percepatan di titik x = 0,25 m pada ujung
kawat setelah bergetar 0,1 sekon adalah:
ap = - π 2 cos (10 π t - π x)
ap = - π 2 cos (10 π.0,1 - π .0,25)
ap = - π 2 cos (π -1/4 π )
= - π 2 cos ( ¾ π)
= - π 2 . (- ½ √2)
ap = ½ √2 π 2 m/s 2

43. (c) Sudut fase dan fase
yp = + A cos 2π (t /T - x/λ )
Sudut fase di titik x = 0,25 m pada ujung kawat
setelah bergetar 0,1 sekon adalah:
θ = 2π (t/T- x/λ) = ¾ π rad
Fase di titik x = 0,25 m pada ujung kawat
setelah bergetar 0,1 sekon adalah:
φ = ¾ π/2π= 3/8