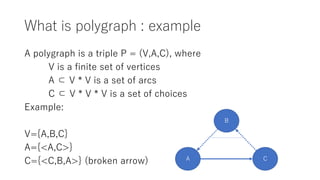
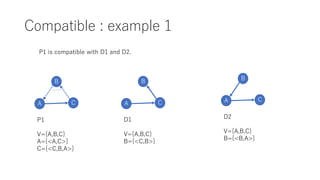
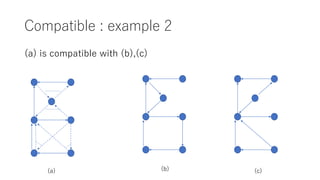
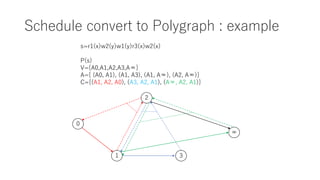
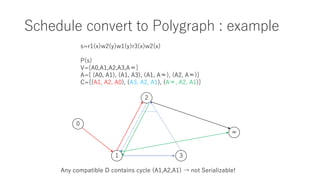
The document discusses converting a schedule validation problem into a polygraph problem to leverage existing polygraph algorithms. It defines what a polygraph is - a triple of vertices, arcs, and choices. It then explains how to construct a polygraph P(s) from a schedule s by making transactions vertices and enforcing ordering/conflict relationships with arcs and choices. Testing if a schedule is conflict-serializable amounts to checking if the corresponding polygraph P(s) has a compatible acyclic directed graph - if so, it is serializable. An example converts a sample schedule into a polygraph to check for cycles.

1. VSR and Polygraph

2. Agenda
- Why we need polygraph
- What is polygraph
- compatible
- Schedule convert to Polygraph

3. Why we need polygraph
• Indicate complexity of VSR
• Schedule Validation for VSR is NP complete
• VSR validation >p cycle detection of Polygraph
• Cycle detection of Polygraph >p 2,3 CNF SAT
• 2,3CNF SAT is NP complete
Note: >p is polynomial reduction

4. What is polygraph
A polygraph is a triple P = (V,A,C), where
V is a finite set of vertices
A ⊂ V * V is a set of arcs
C ⊂ V * V * V is a set of choices
Note:If(u,v,w)∈C, then the three vertices are necessarily
distinct, and in fact (w,u)∈A

5. What is polygraph : example
A polygraph is a triple P = (V,A,C), where
V is a finite set of vertices
A ⊂ V * V is a set of arcs
C ⊂ V * V * V is a set of choices
Example:
V={A,B,C}
A={<A,C>}
C={<C,B,A>} (broken arrow) A
B
C

6. Compatible
- Suppose
- P = (V,A,C) is a polygraph
- D = (V,B) be a directed graph
- We say that D is compatible with P
- if
- A ⊂ B and,
- Each choice(u,v,w)∈C either (u,v)∈B or (v,w) ∈ B

7. Compatible : example 1
A
B
C
P1
V={A,B,C}
A={<A,C>}
C={<C,B,A>}
A
B
C
D1
V={A,B,C}
B={<C,B>}
A
B
C
D2
V={A,B,C}
B={<B,A>}
P1 is compatible with D1 and D2.

8. Compatible : example 2
(a) is compatible with (b),(c)
(c)(a) (b)

9. Compatible : acyclic
• Polygraph P is called acyclic
• if there is an acyclic directed graph D
• that is compatible with P
↓ summarize
• If compatible DAG exists, Polygraph is acyclic.

10. Schedule convert to Polygraph
P(s): Polygraph of s
Vertices V: all transactions in s^= s+ A0, A∞
Arcs A: R2(x)∈A2, W1(x)∈A1,
W1(x) < R2(x),
arc(A1,A2)
Choices C: W1(s) < R2(x) ∧ ∃(W3(x)∈A3)
choise(A2,A3,A1)

11. Schedule convert to Polygraph : example
s=r1(x)w2(y)w1(y)r3(x)w2(x)
A1: R(x) W(y)
A2: W(y) W(x)
A3: R(y)
P(s)

12. Schedule convert to Polygraph : example
s=r1(x)w2(y)w1(y)r3(x)w2(x)
A0:W(x)W(y)
A1: R(x) W(y)
A2: W(y) W(x)
A3: R(y)
A∞: R(x)R(y)
P(s)
V={A0,A1,A2,A3,A∞}
Vertices V: all transactions in s^= s+ A0, A∞

13. Schedule convert to Polygraph : example
s=r1(x)w2(y)w1(y)r3(x)w2(x)
A0:W(x)W(y)
A1: R(x) W(y)
A2: W(y) W(x)
A3: R(y)
A∞: R(x)R(y)
P(s)
V={A0,A1,A2,A3,A∞}
A={ (A0, A1), (A1, A3), (A1, A∞), (A2, A∞)}
Arcs A: R2(x)∈A2, W1(x)∈A1, W1(x) < R2(x), arc(A1,A2)

14. Schedule convert to Polygraph : example
s=r1(x)w2(y)w1(y)r3(x)w2(x)
A0:W(x)W(y)
A1: R(x) W(y)
A2: W(y) W(x)
A3: R(y)
A∞: R(x)R(y)
P(s)
V={A0,A1,A2,A3,A∞}
A={ (A0, A1), (A1, A3), (A1, A∞), (A2, A∞)}
C={(A1, A2, A0)}
Choices C: W1(s) < R2(x) ∧ W3(x), choise(A2,A3,A1)

15. Schedule convert to Polygraph : example
s=r1(x)w2(y)w1(y)r3(x)w2(x)
A0:W(x)W(y)
A1: R(x) W(y)
A2: W(y) W(x)
A3: R(y)
A∞: R(x)R(y)
P(s)
V={A0,A1,A2,A3,A∞}
A={ (A0, A1), (A1, A3), (A1, A∞), (A2, A∞)}
C={(A1, A2, A0), (A3, A2, A1)}
Choices C: W1(s) < R2(x) ∧ W3(x), choise(A2,A3,A1)

16. Schedule convert to Polygraph : example
s=r1(x)w2(y)w1(y)r3(x)w2(x)
A0:W(x)W(y)
A1: R(x) W(y)
A2: W(y) W(x)
A3: R(y)
A∞: R(x)R(y)
P(s)
V={A0,A1,A2,A3,A∞}
A={ (A0, A1), (A1, A3), (A1, A∞), (A2, A∞)}
C={(A1, A2, A0), (A3, A2, A1), (A∞, A2, A1)}
Choices C: W1(s) < R2(x) ∧ W3(x), choise(A2,A3,A1)

17. Schedule convert to Polygraph : example
s=r1(x)w2(y)w1(y)r3(x)w2(x)
P(s)
V={A0,A1,A2,A3,A∞}
A={ (A0, A1), (A1, A3), (A1, A∞), (A2, A∞)}
C={(A1, A2, A0), (A3, A2, A1), (A∞, A2, A1)}

18. Schedule convert to Polygraph : example
s=r1(x)w2(y)w1(y)r3(x)w2(x)
P(s)
V={A0,A1,A2,A3,A∞}
A={ (A0, A1), (A1, A3), (A1, A∞), (A2, A∞)}
C={(A1, A2, A0), (A3, A2, A1), (A∞, A2, A1)}
0
1
2
3
∞

19. Schedule convert to Polygraph : example
s=r1(x)w2(y)w1(y)r3(x)w2(x)
P(s)
V={A0,A1,A2,A3,A∞}
A={ (A0, A1), (A1, A3), (A1, A∞), (A2, A∞)}
C={(A1, A2, A0), (A3, A2, A1), (A∞, A2, A1)}
0
1
2
3
∞
Any compatible D contains cycle (A1,A2,A1) → not Serializable!