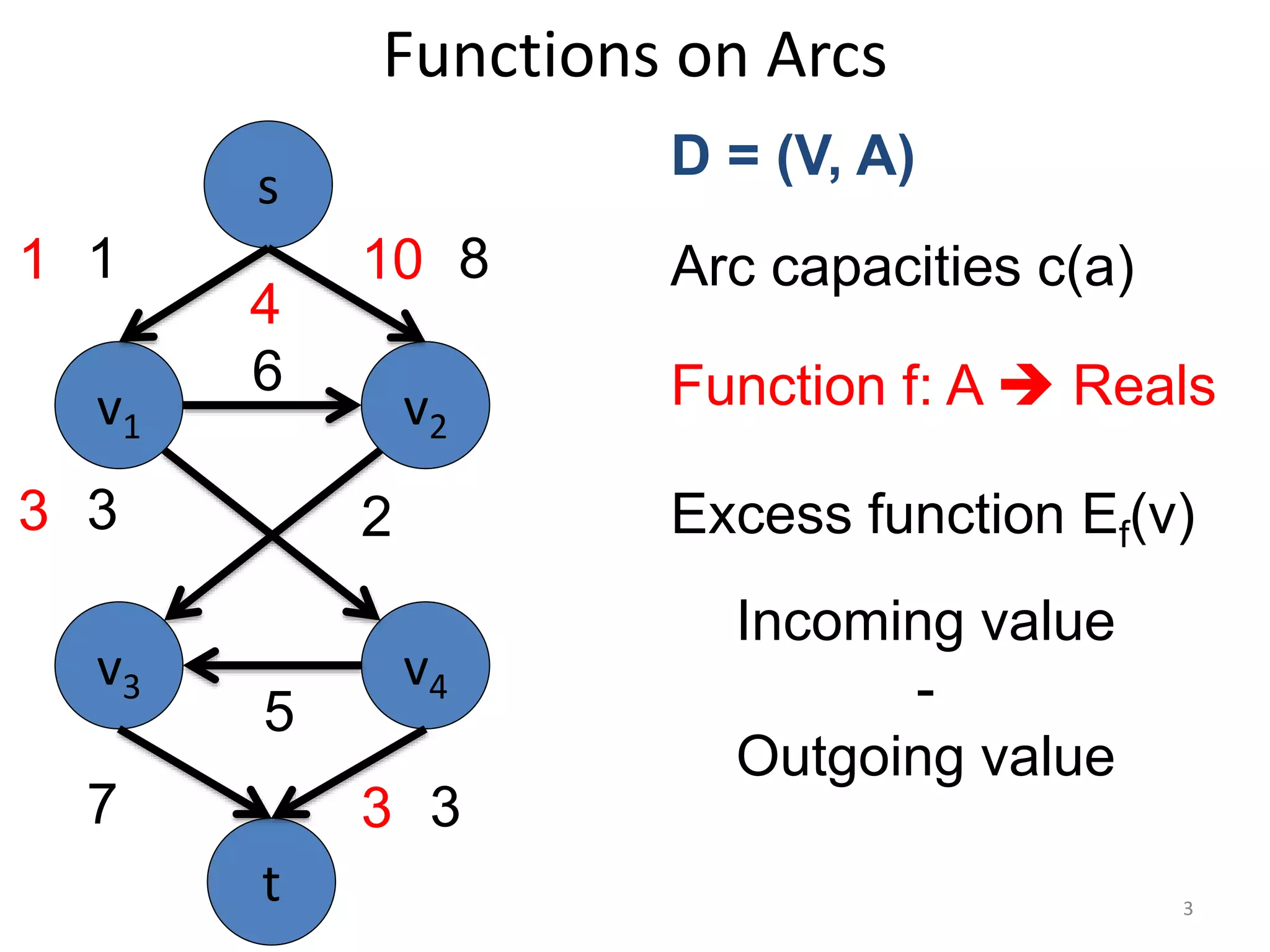
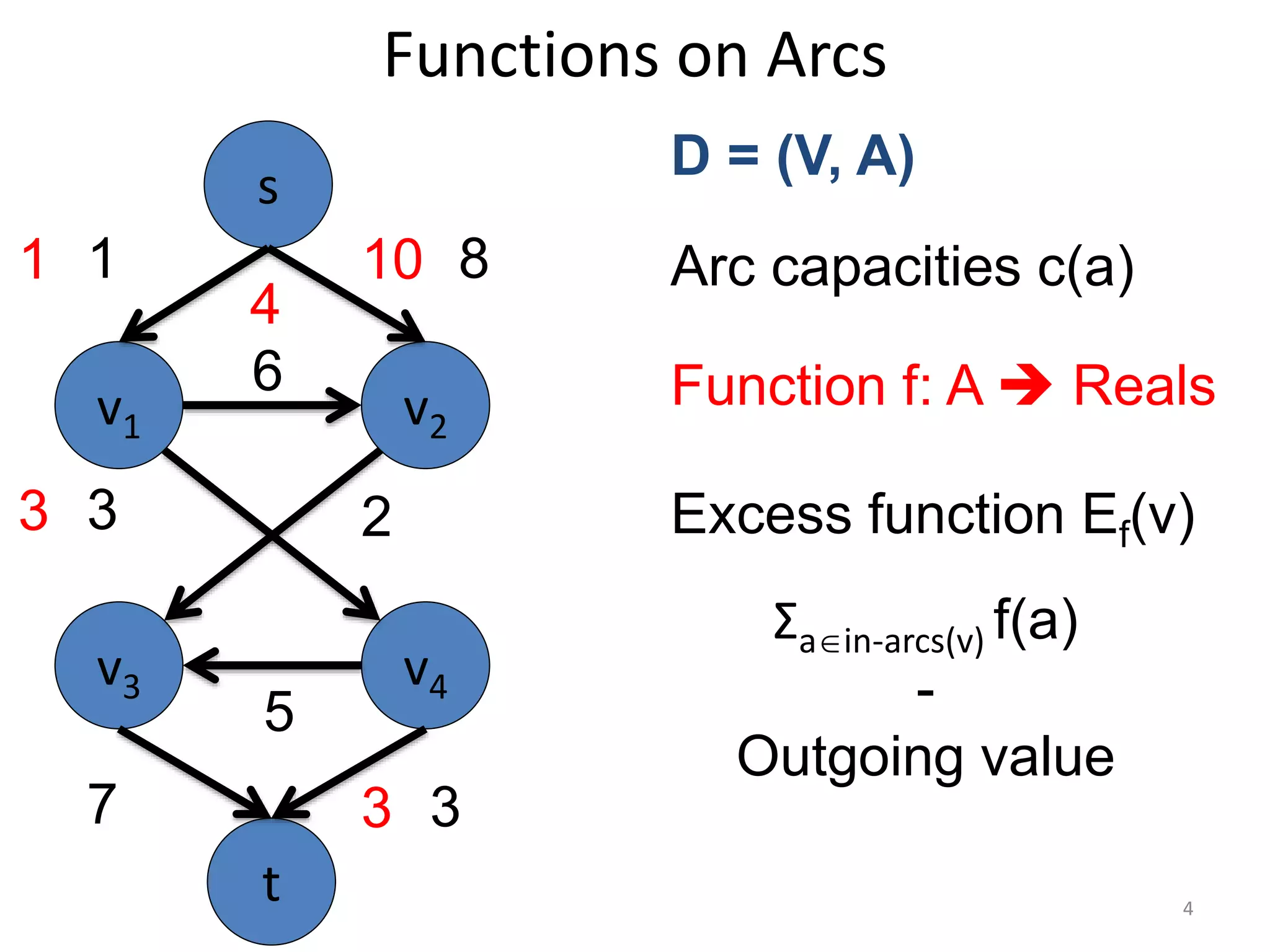
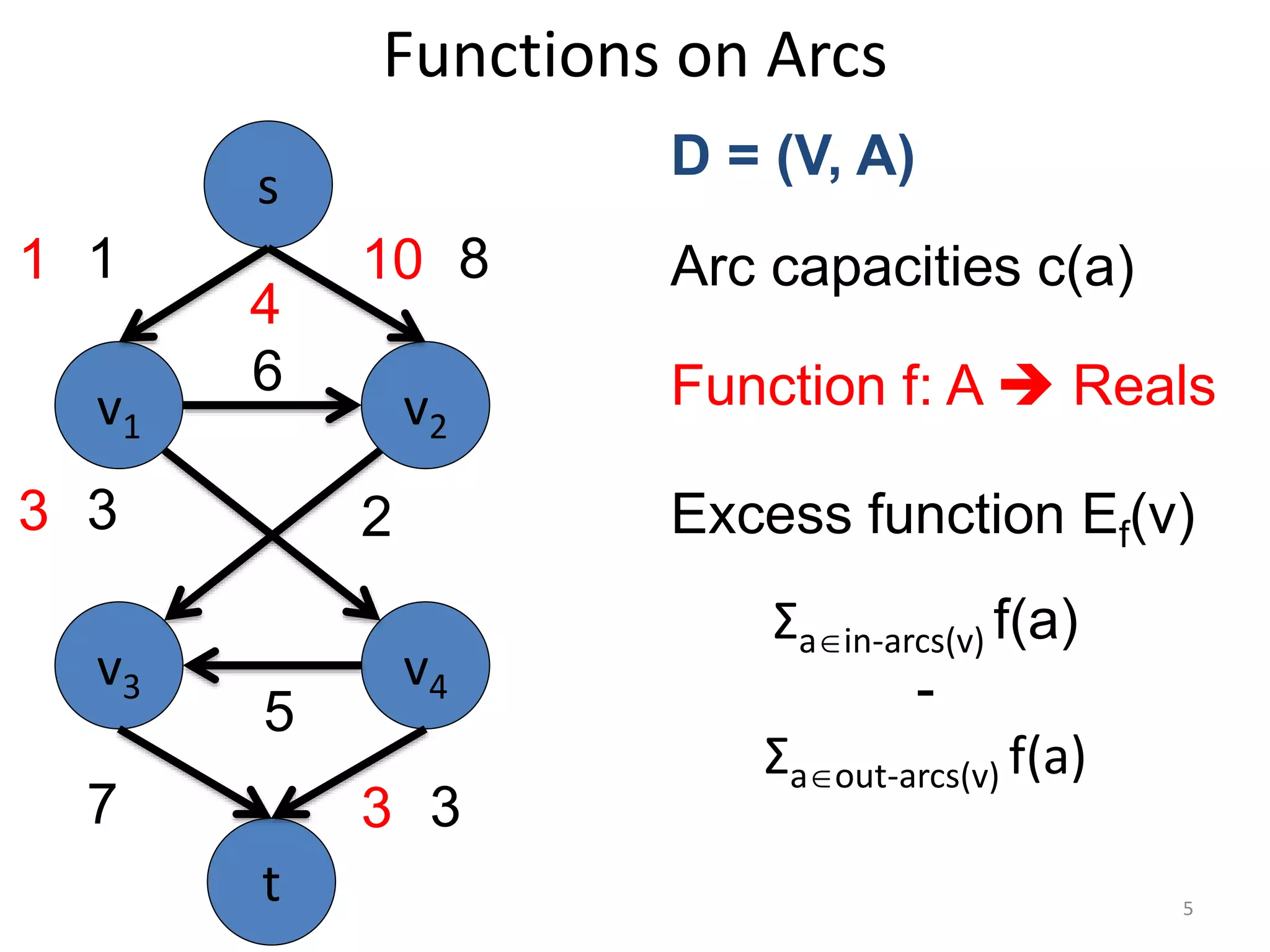
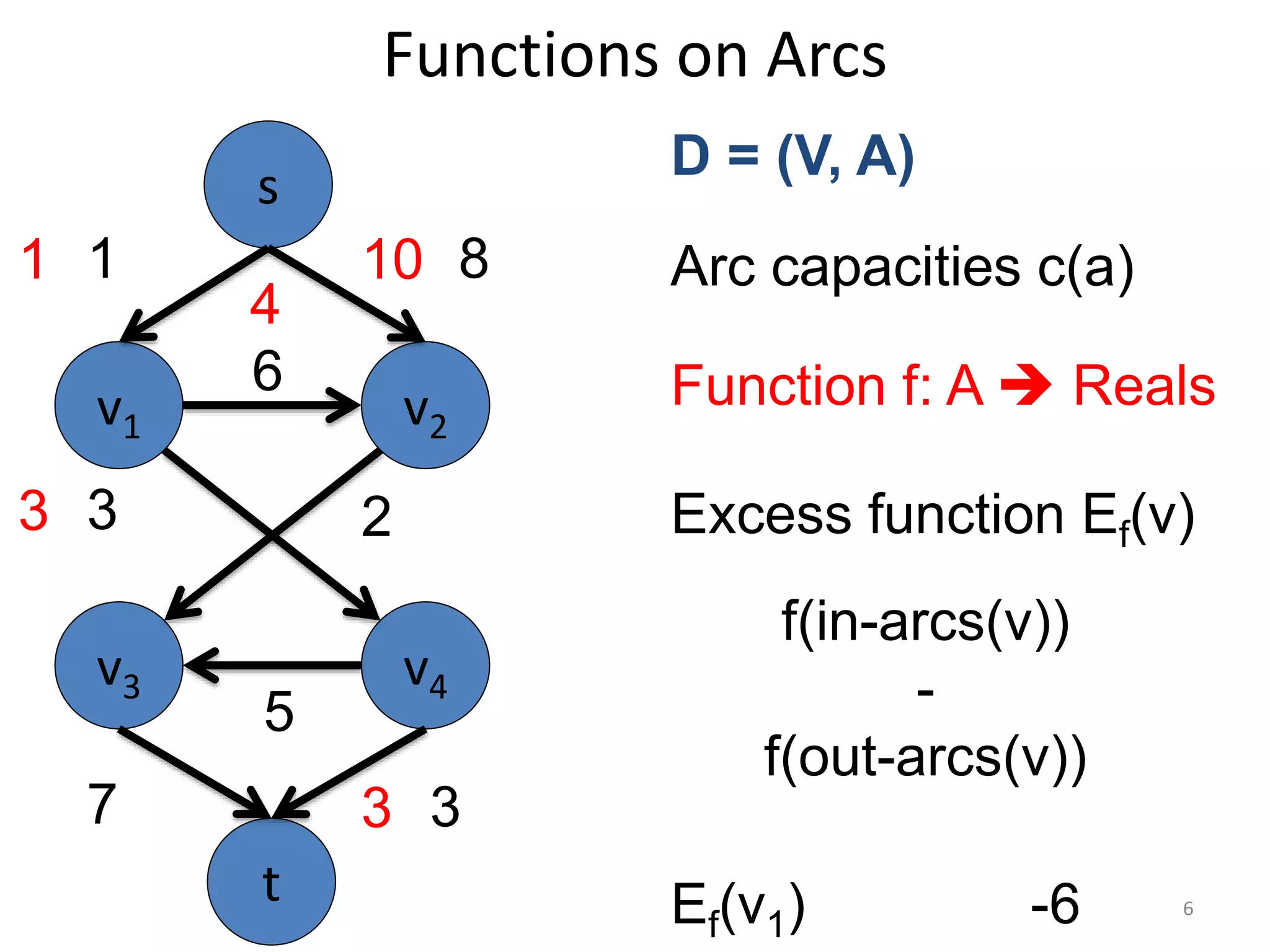
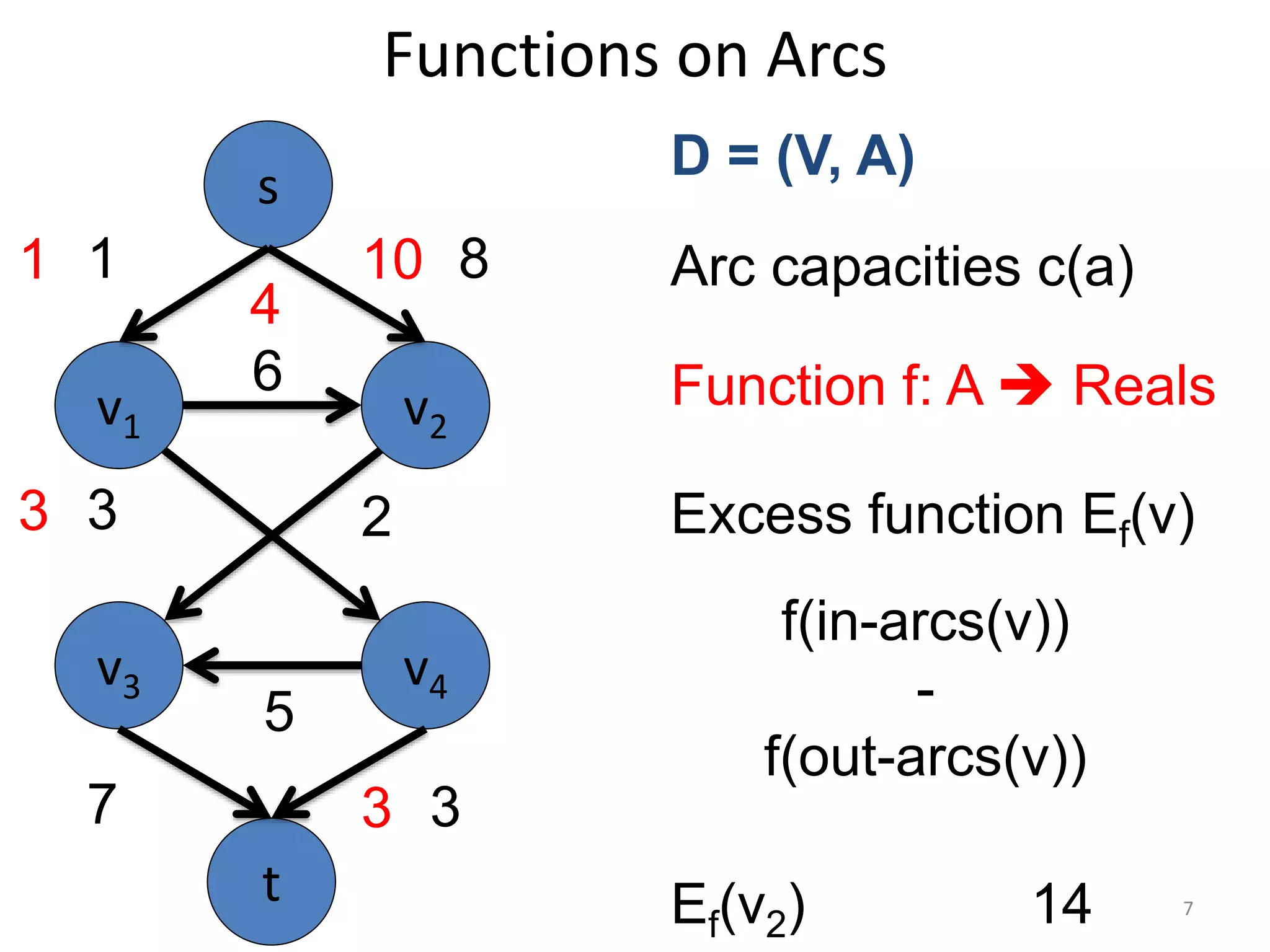
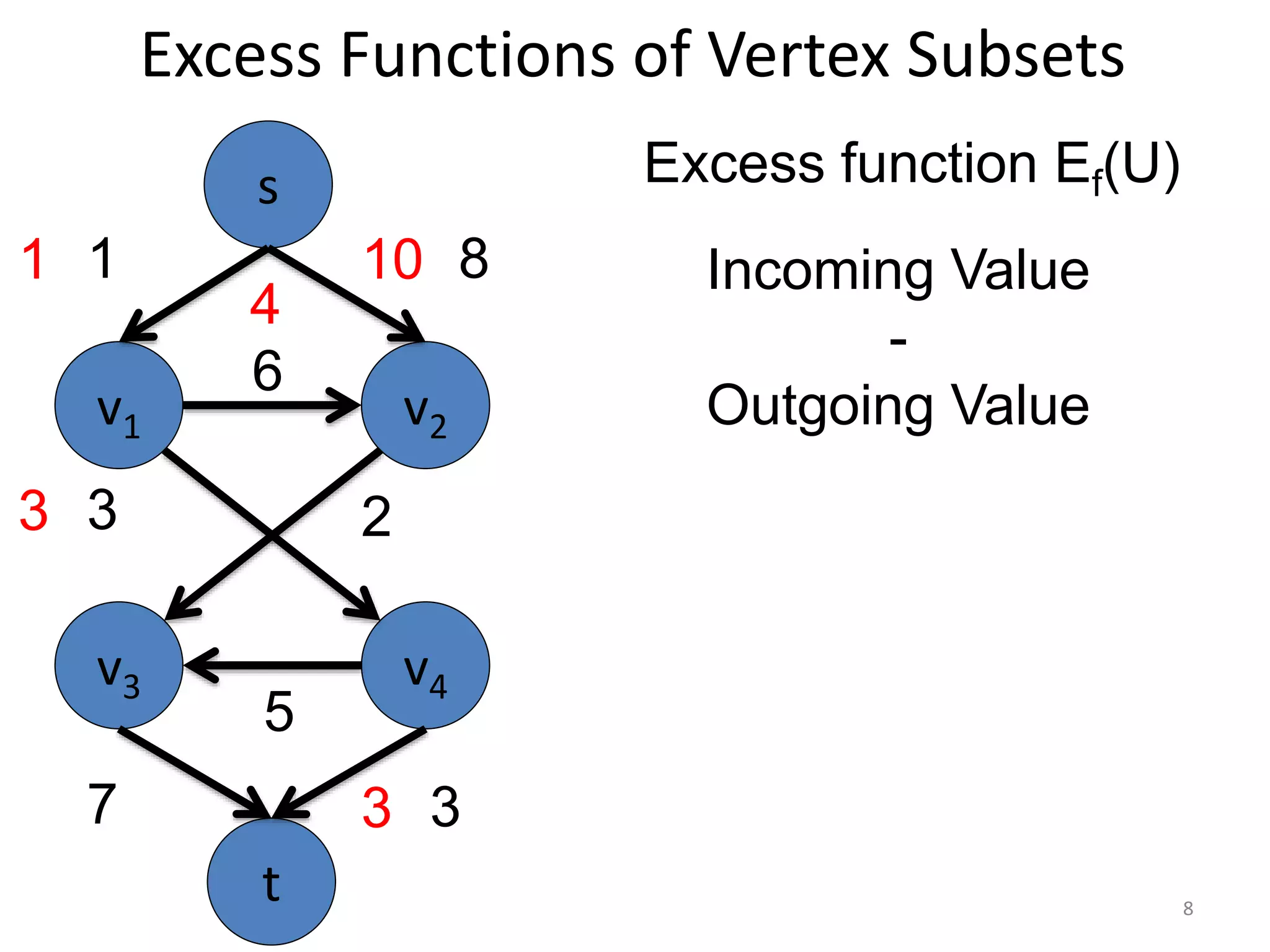
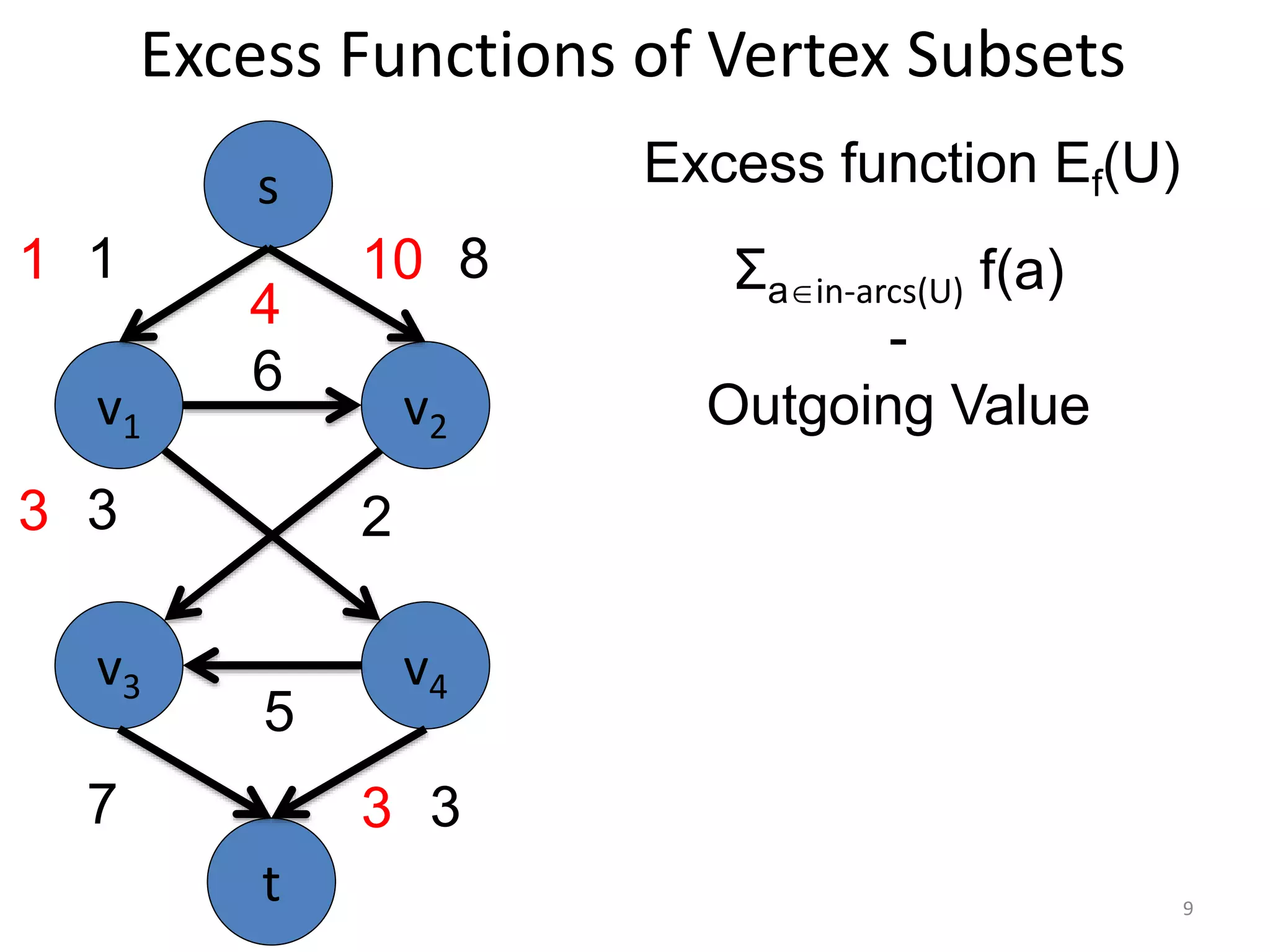
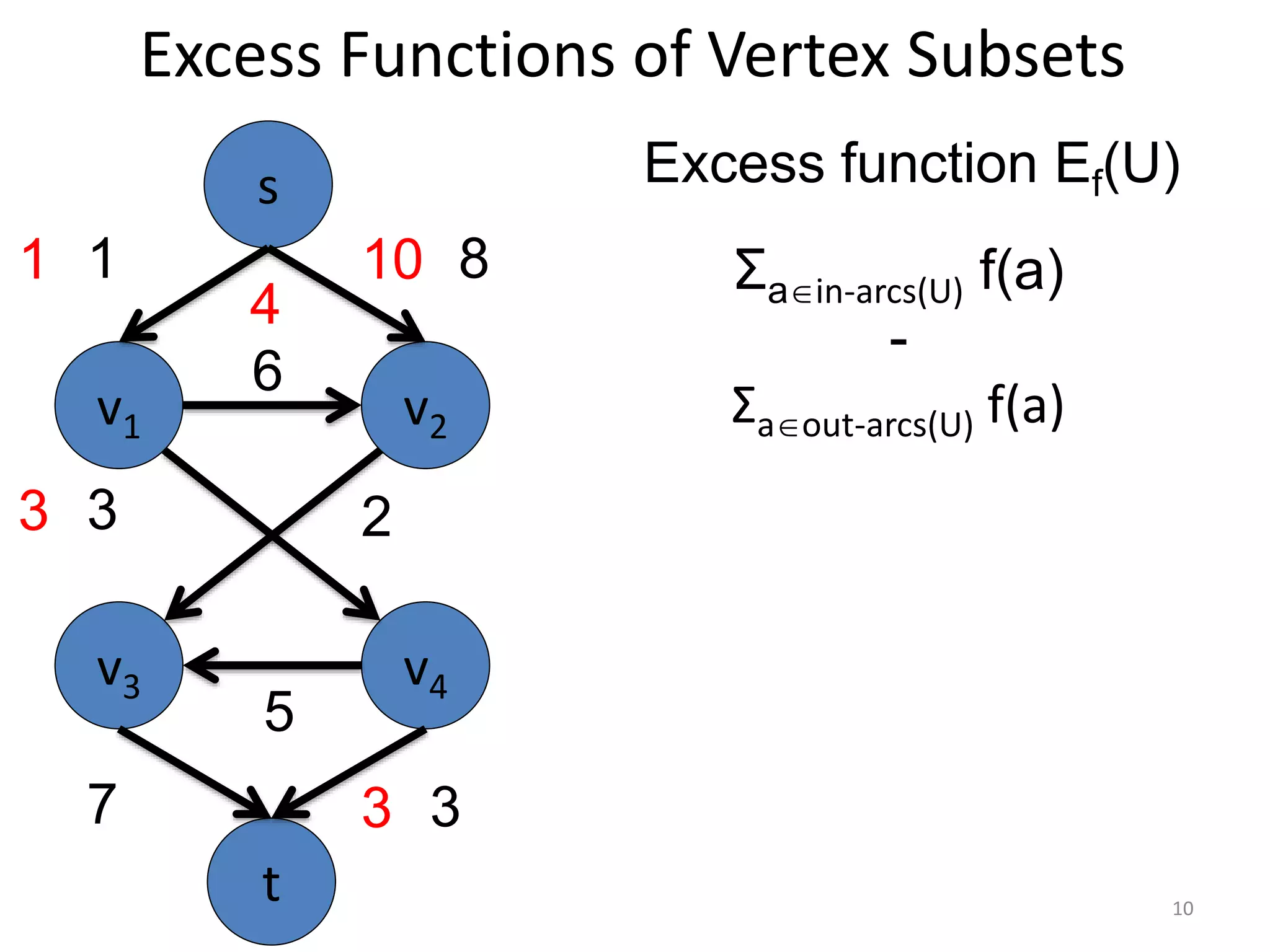
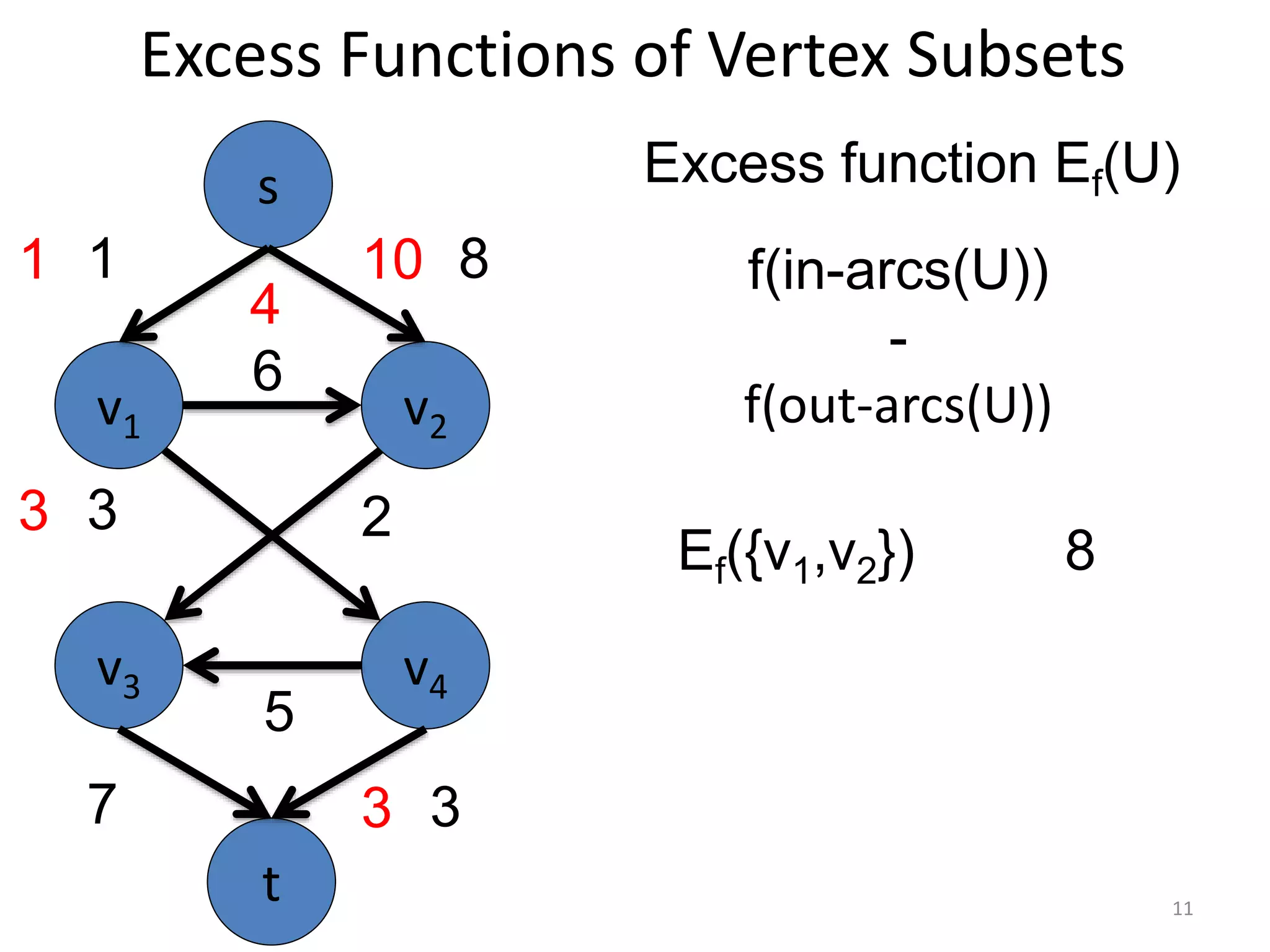
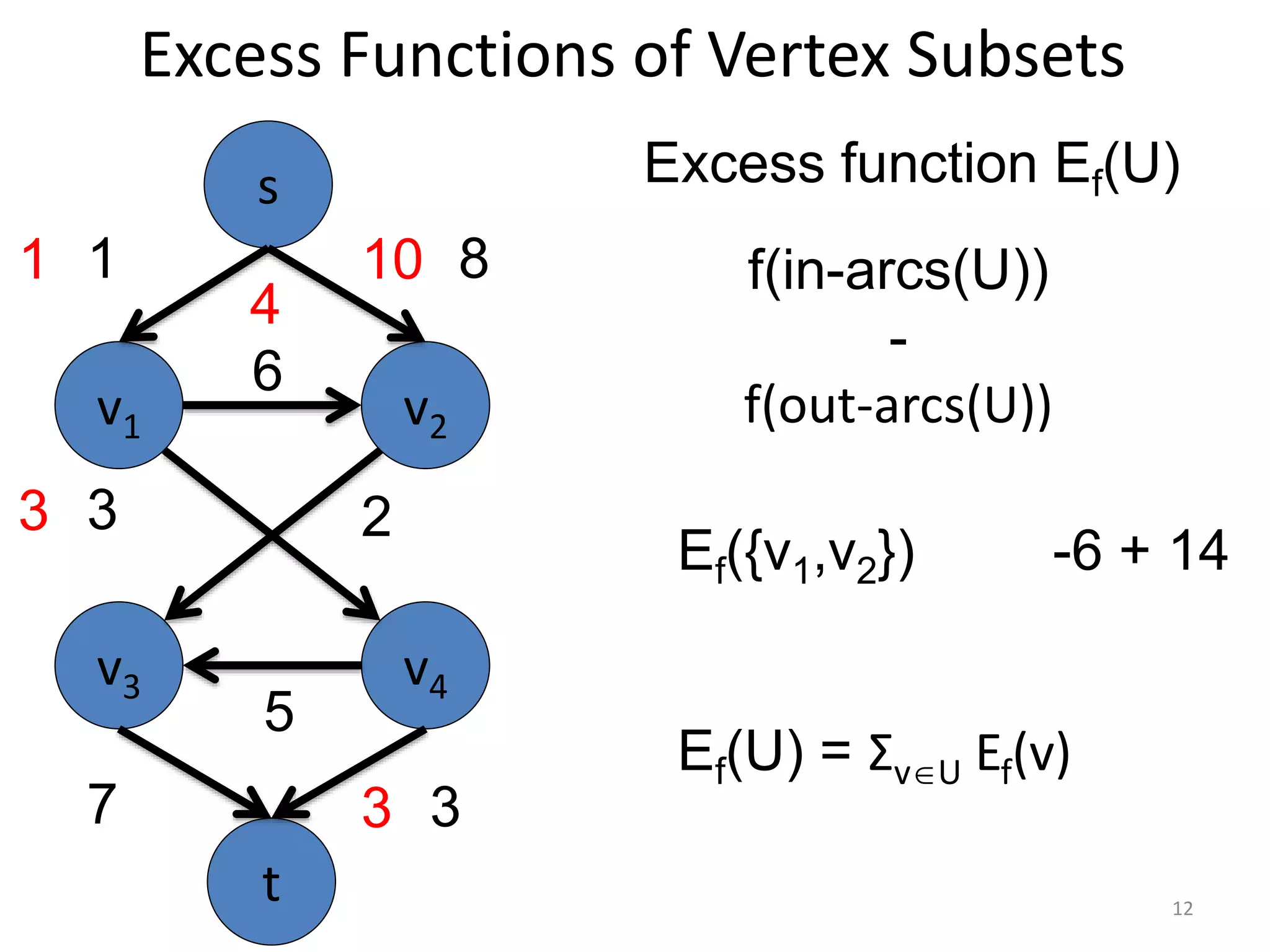
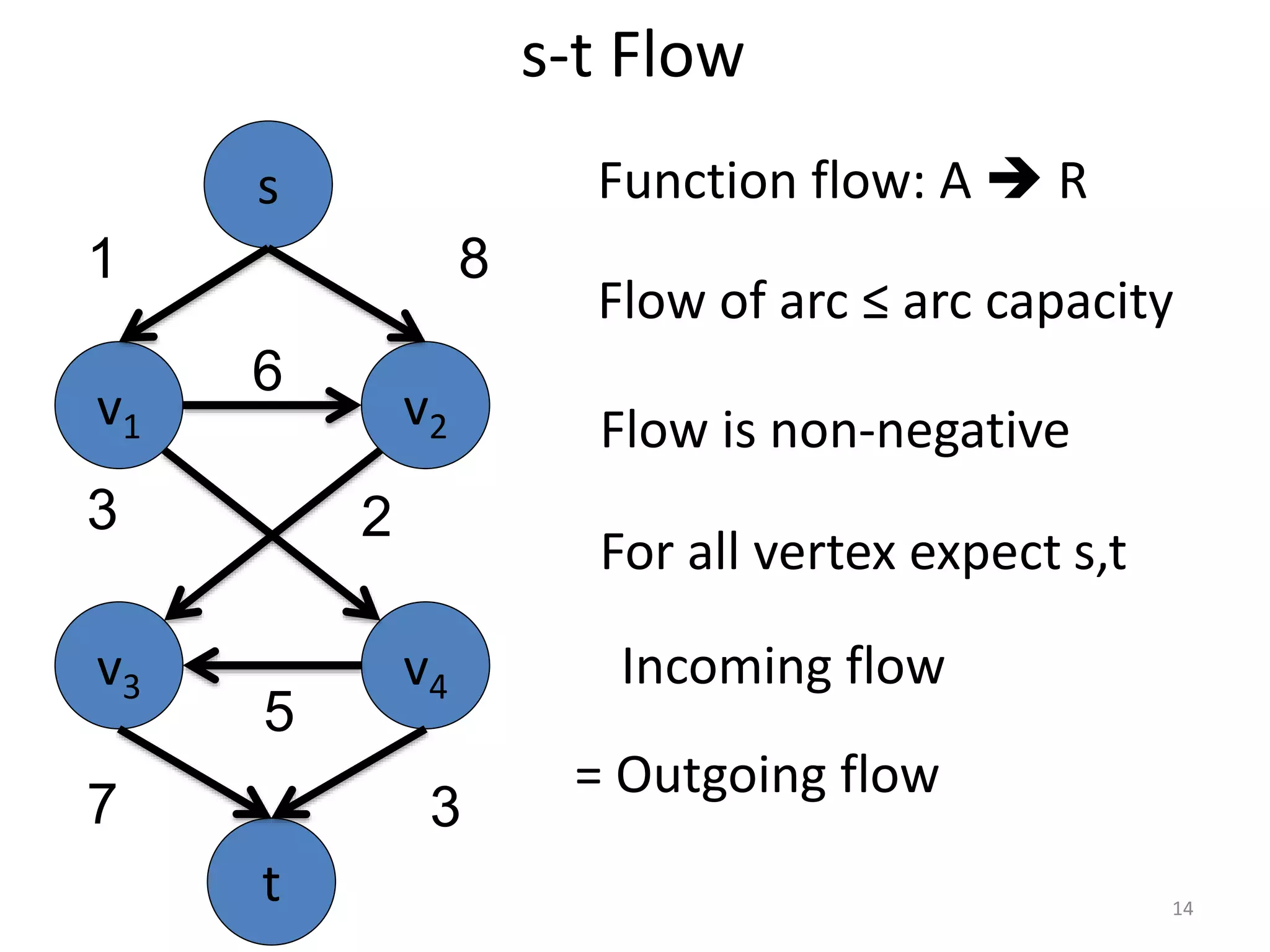
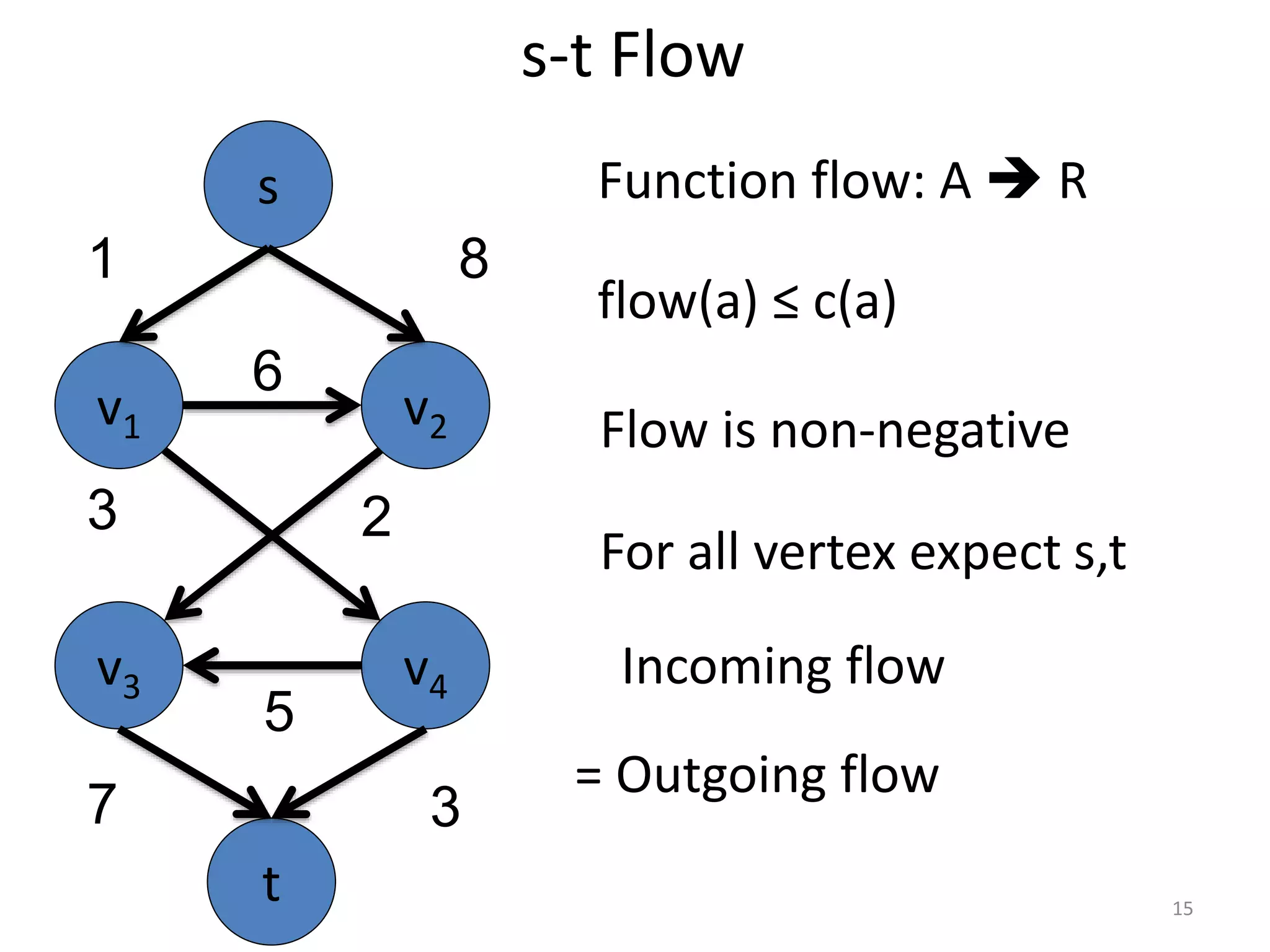
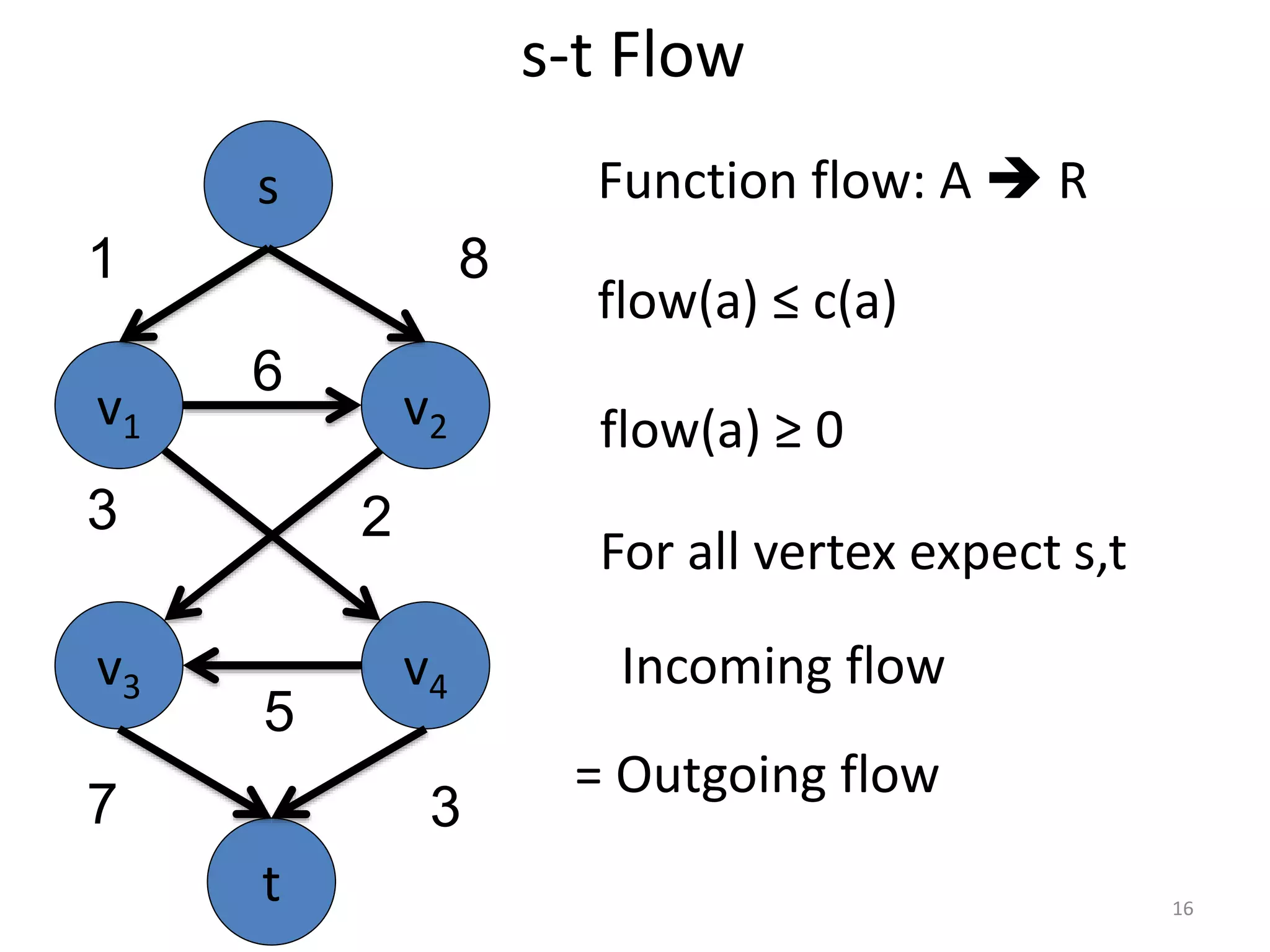
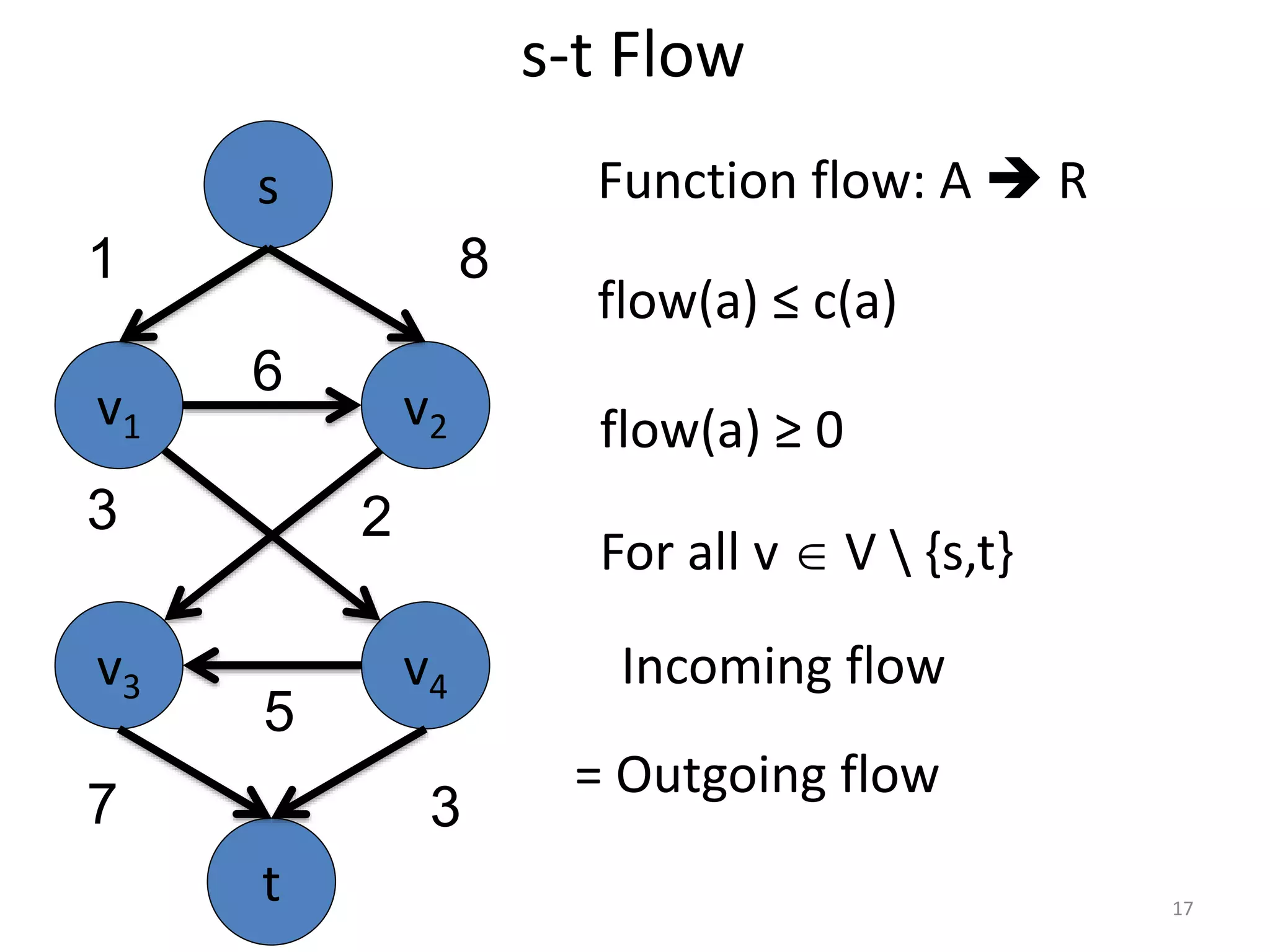
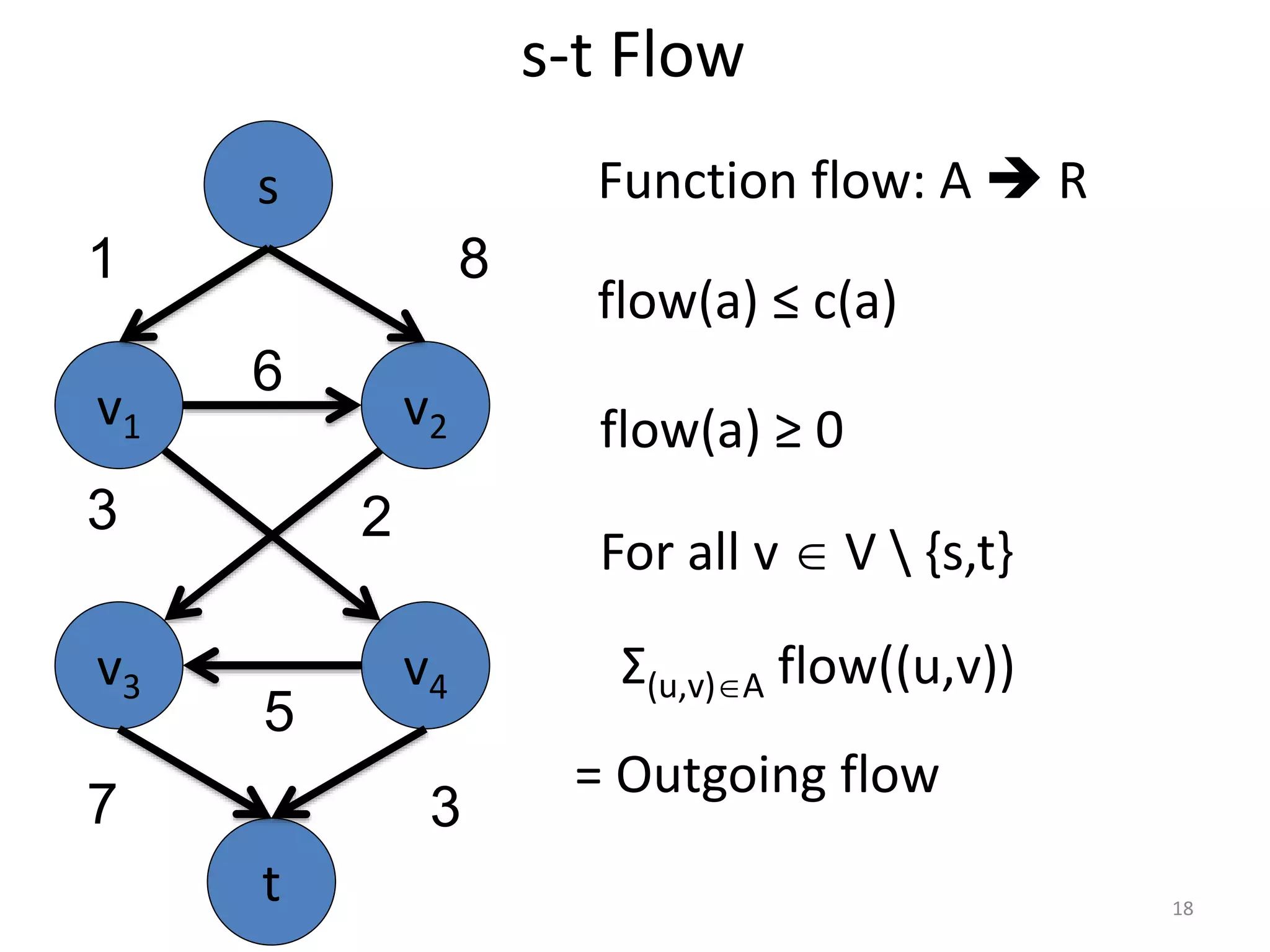
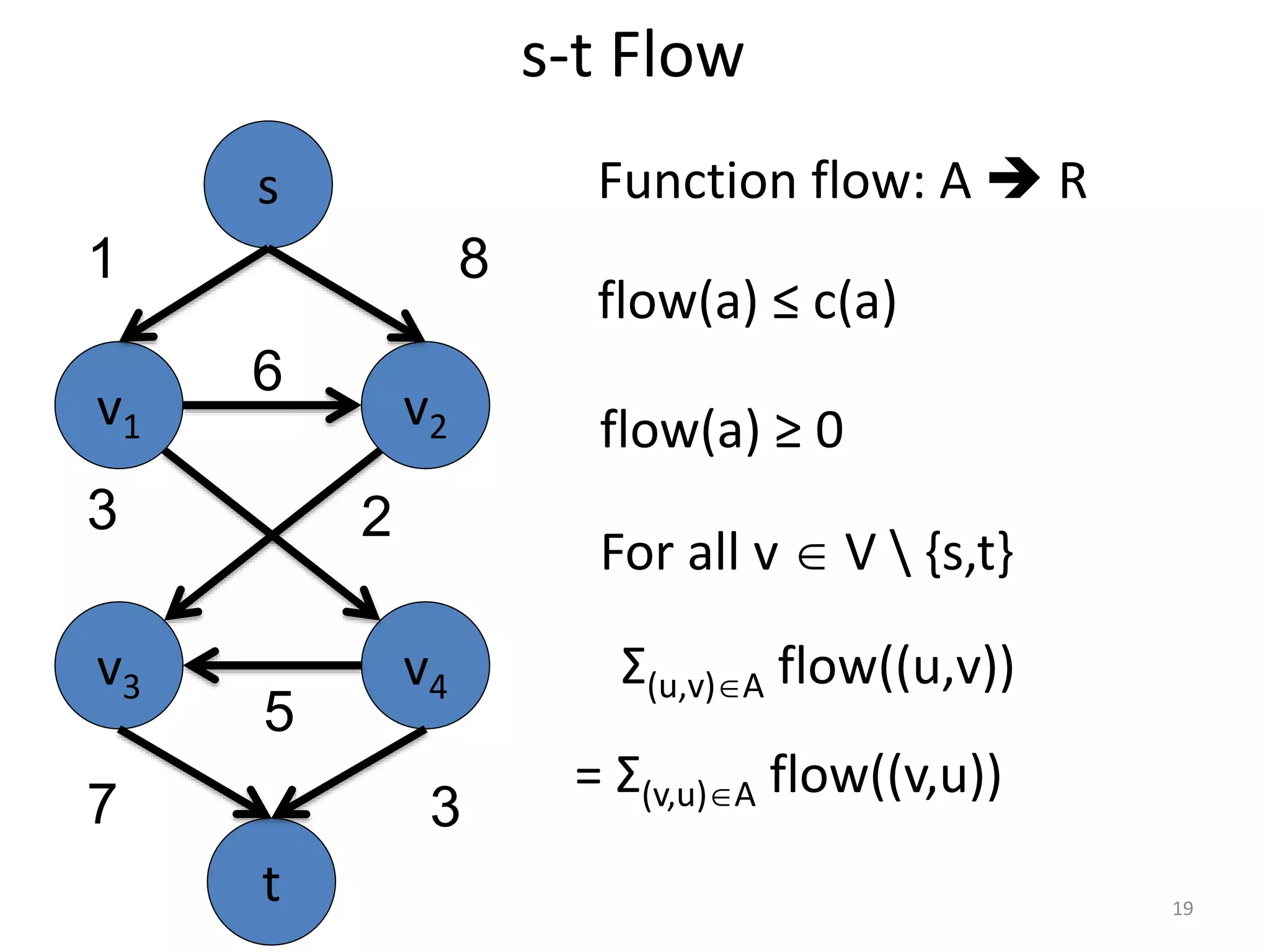
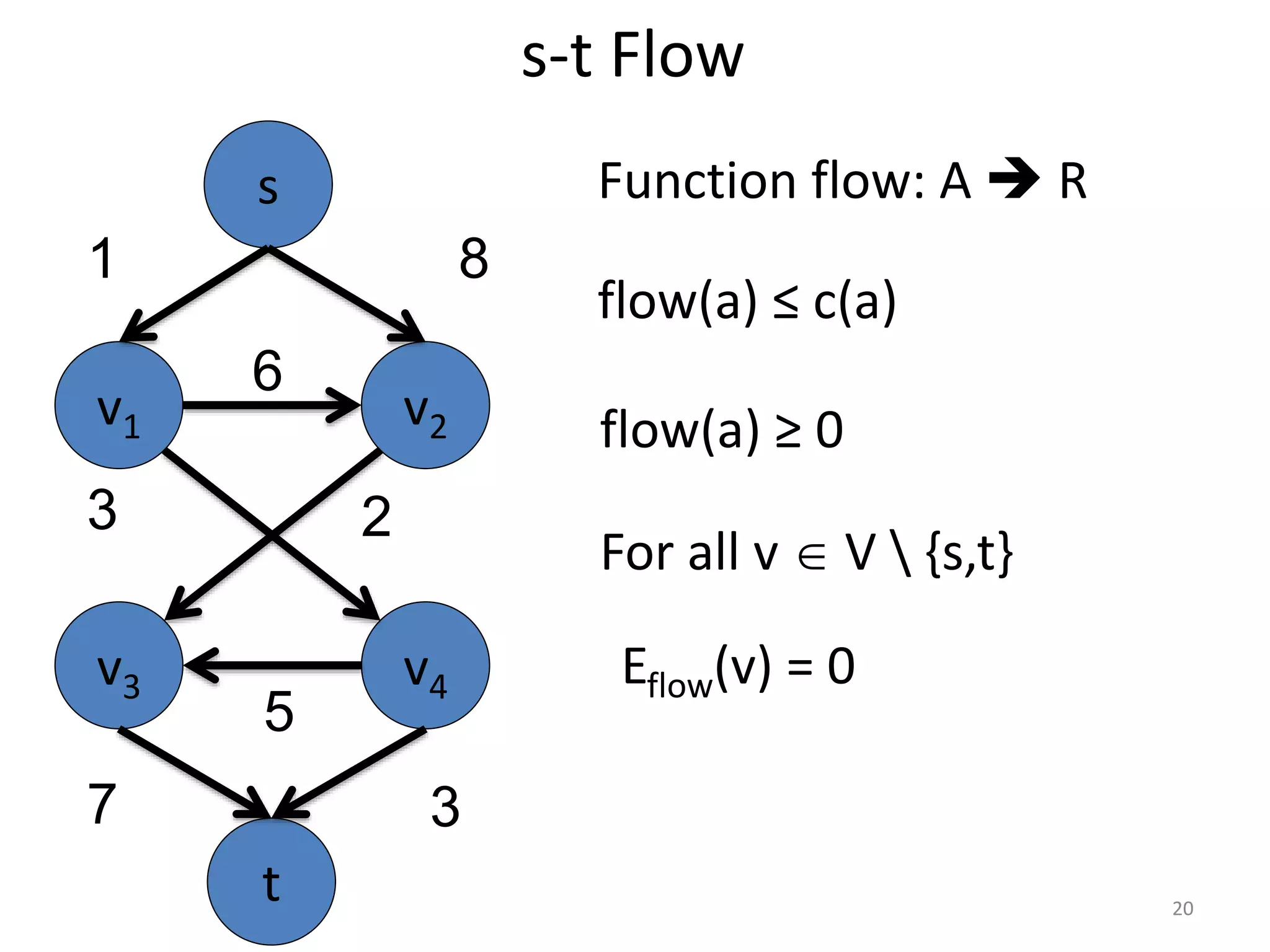
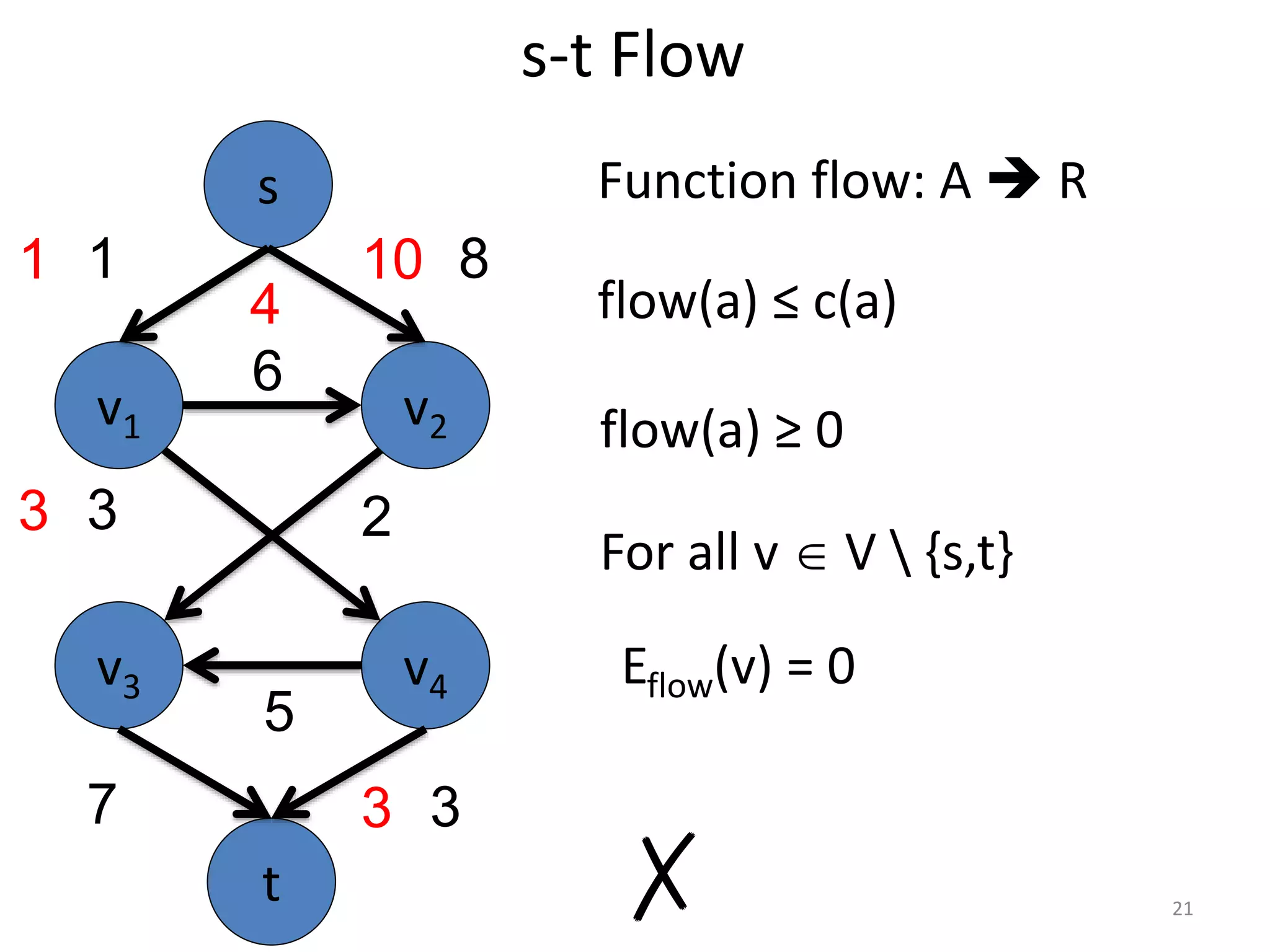
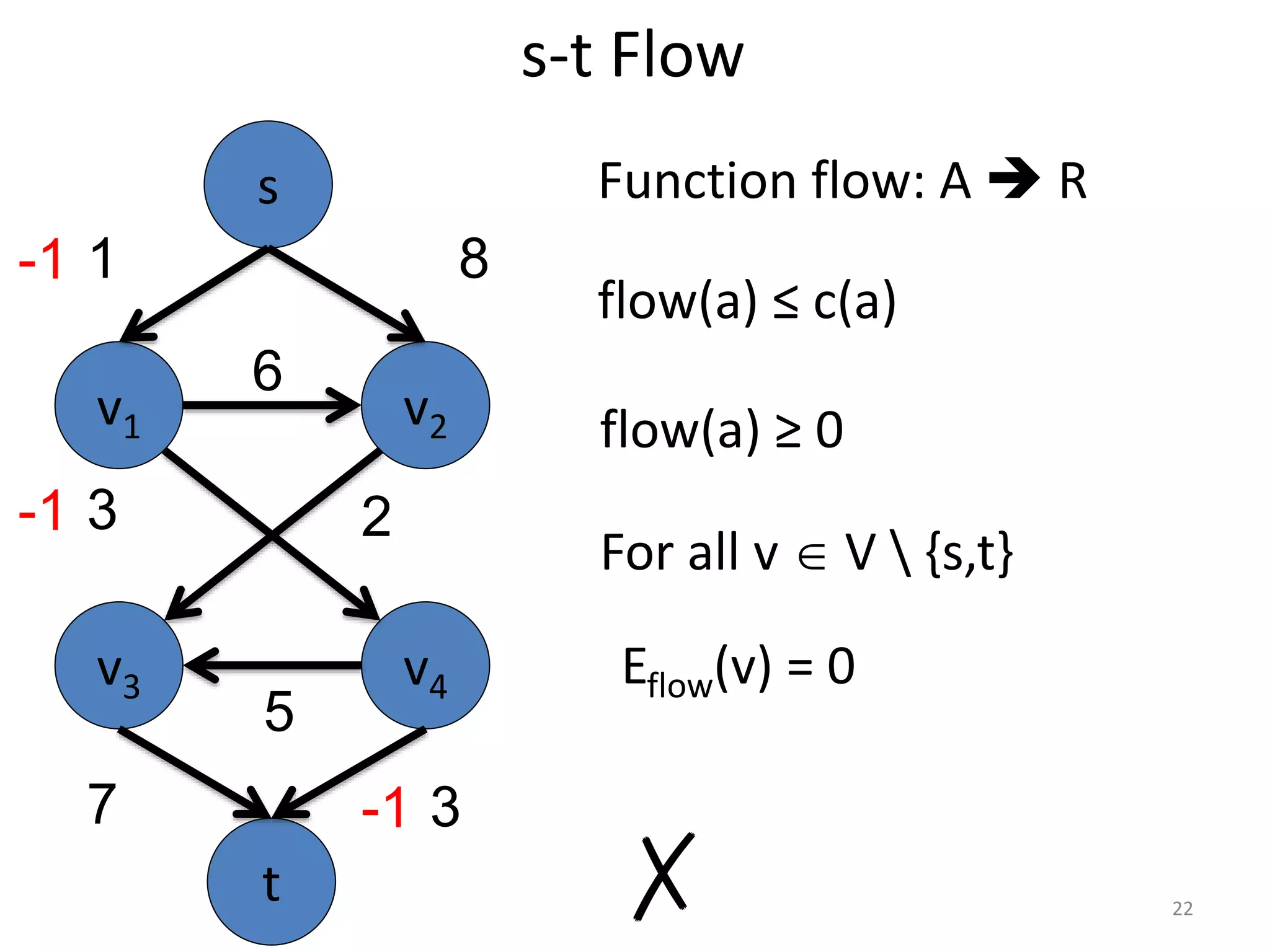
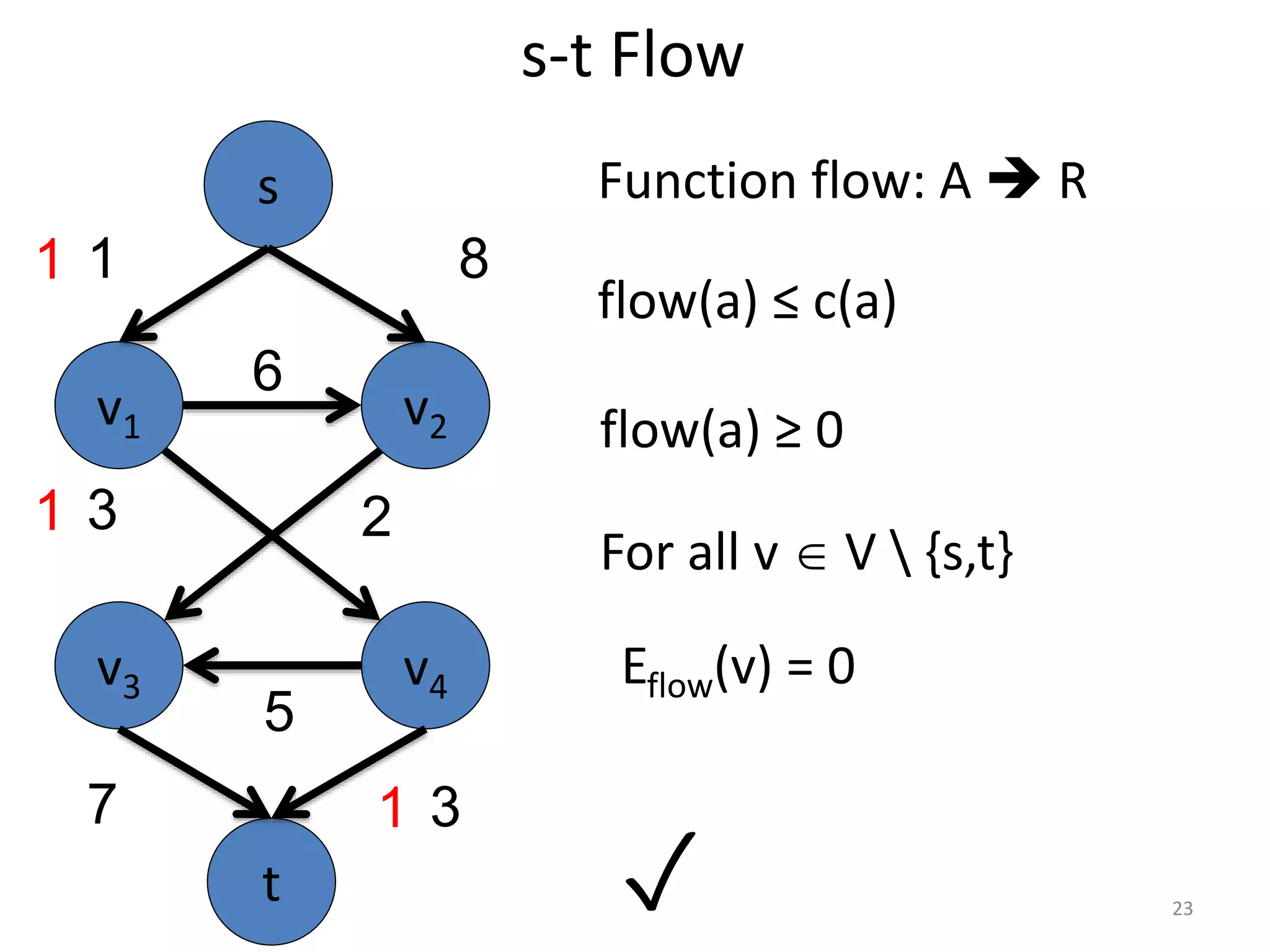
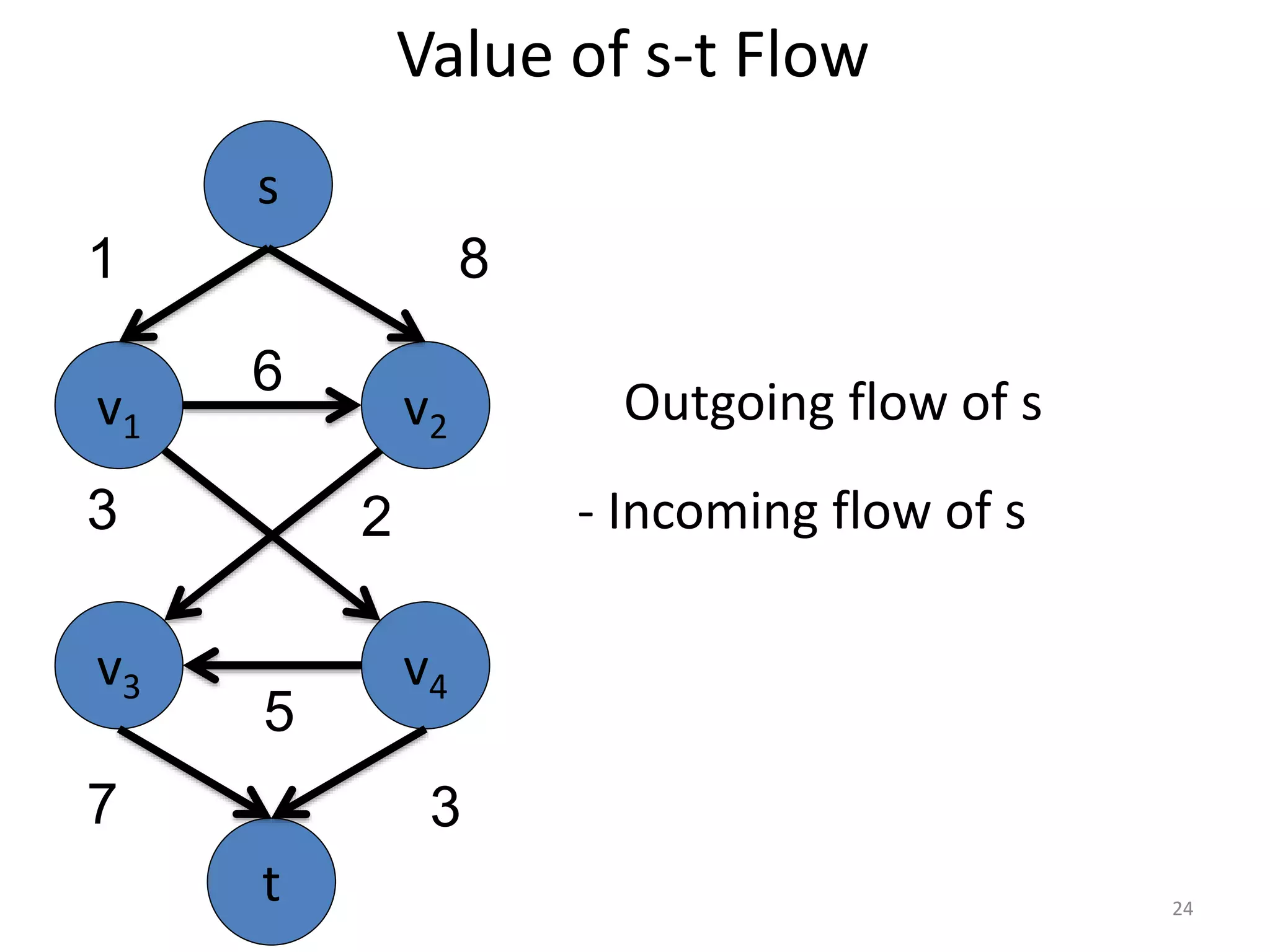
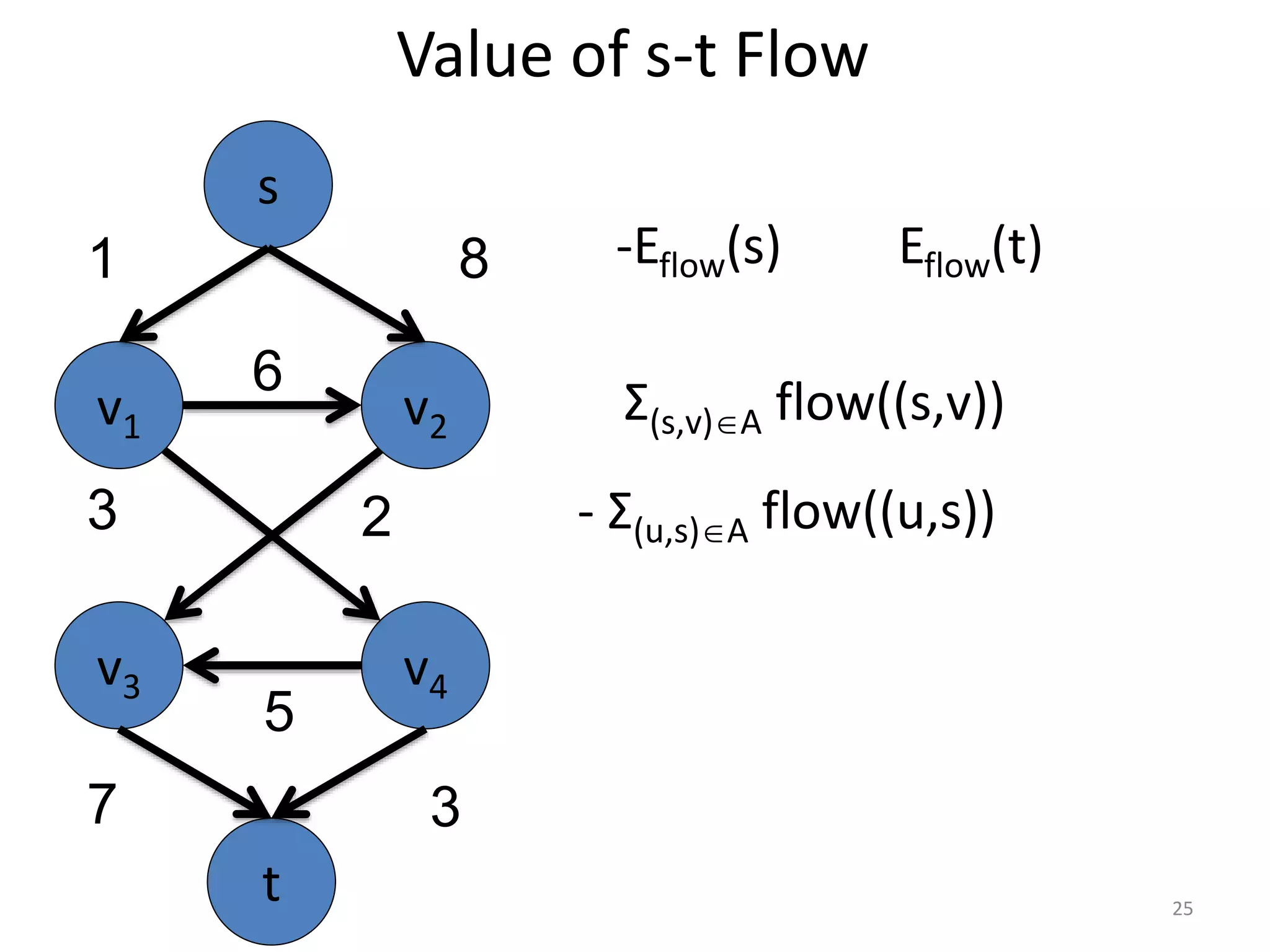
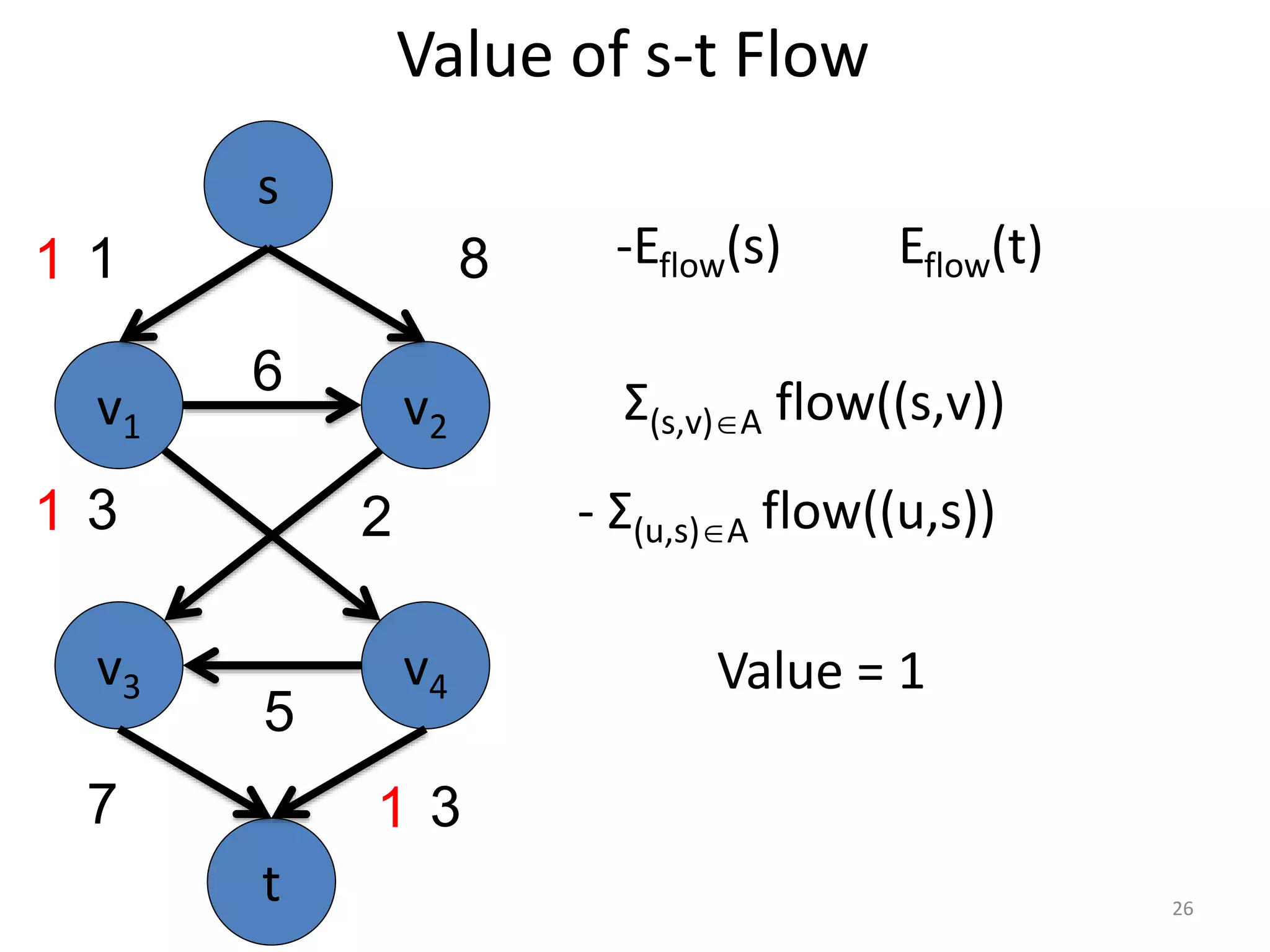
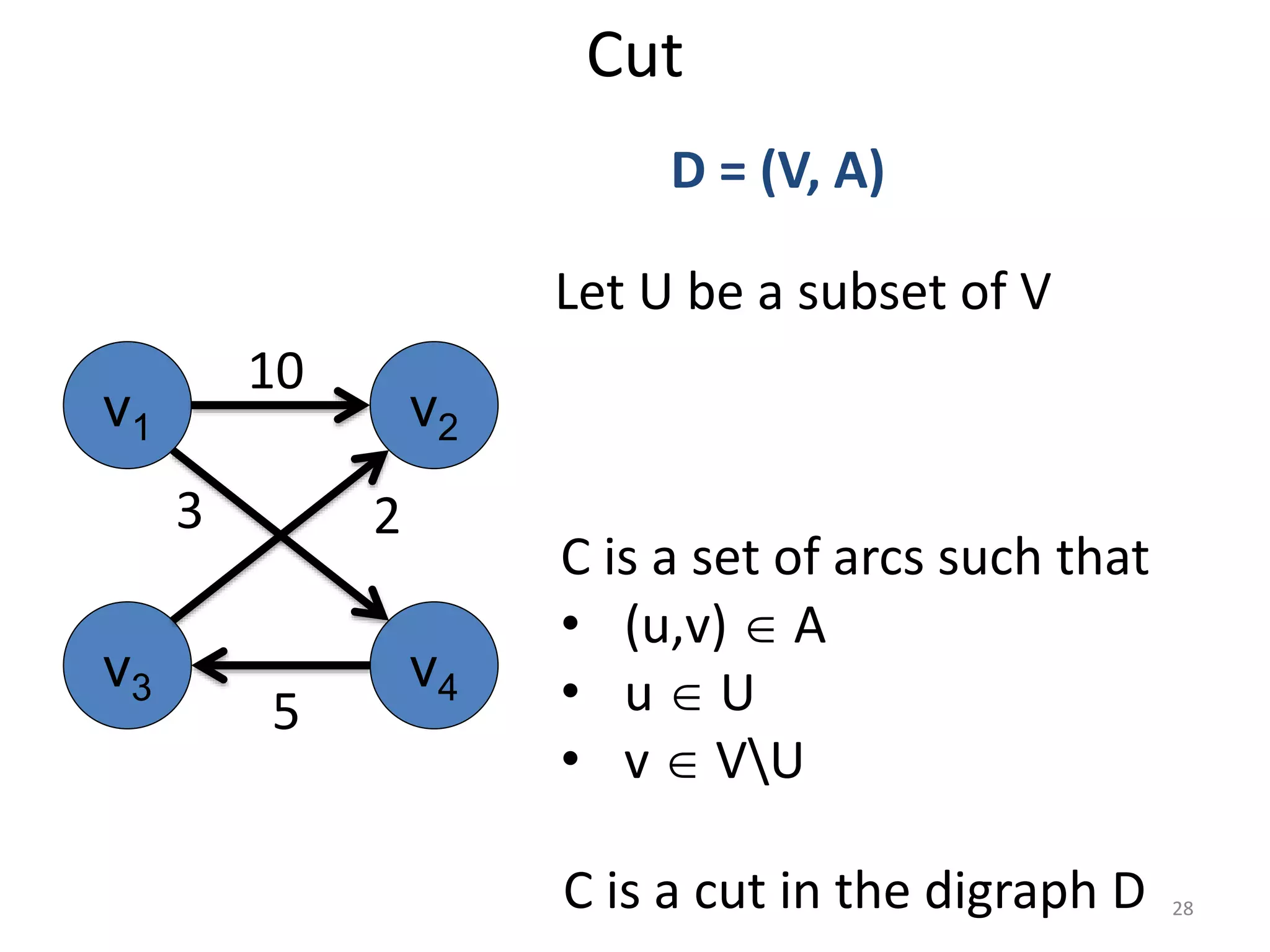
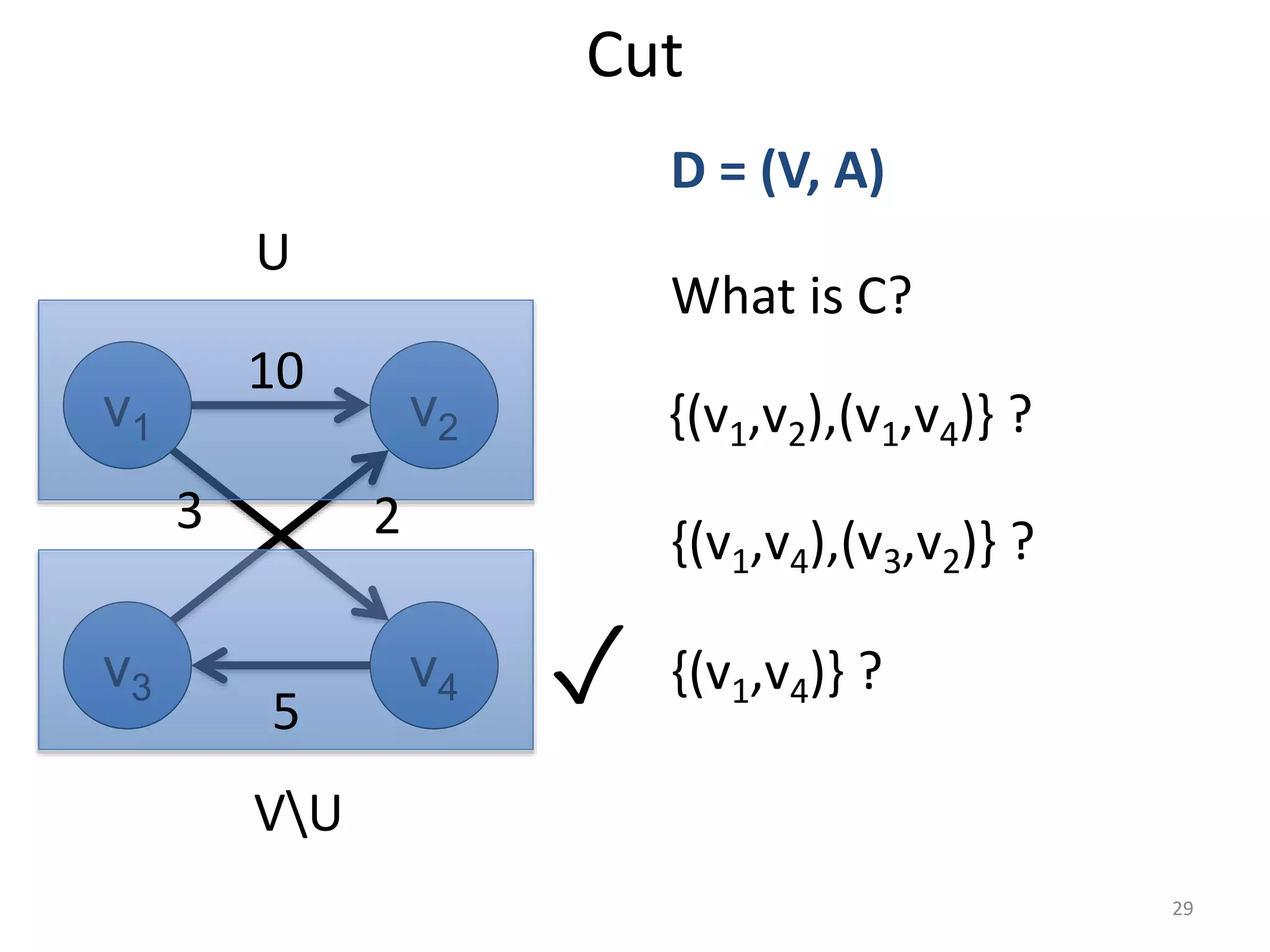
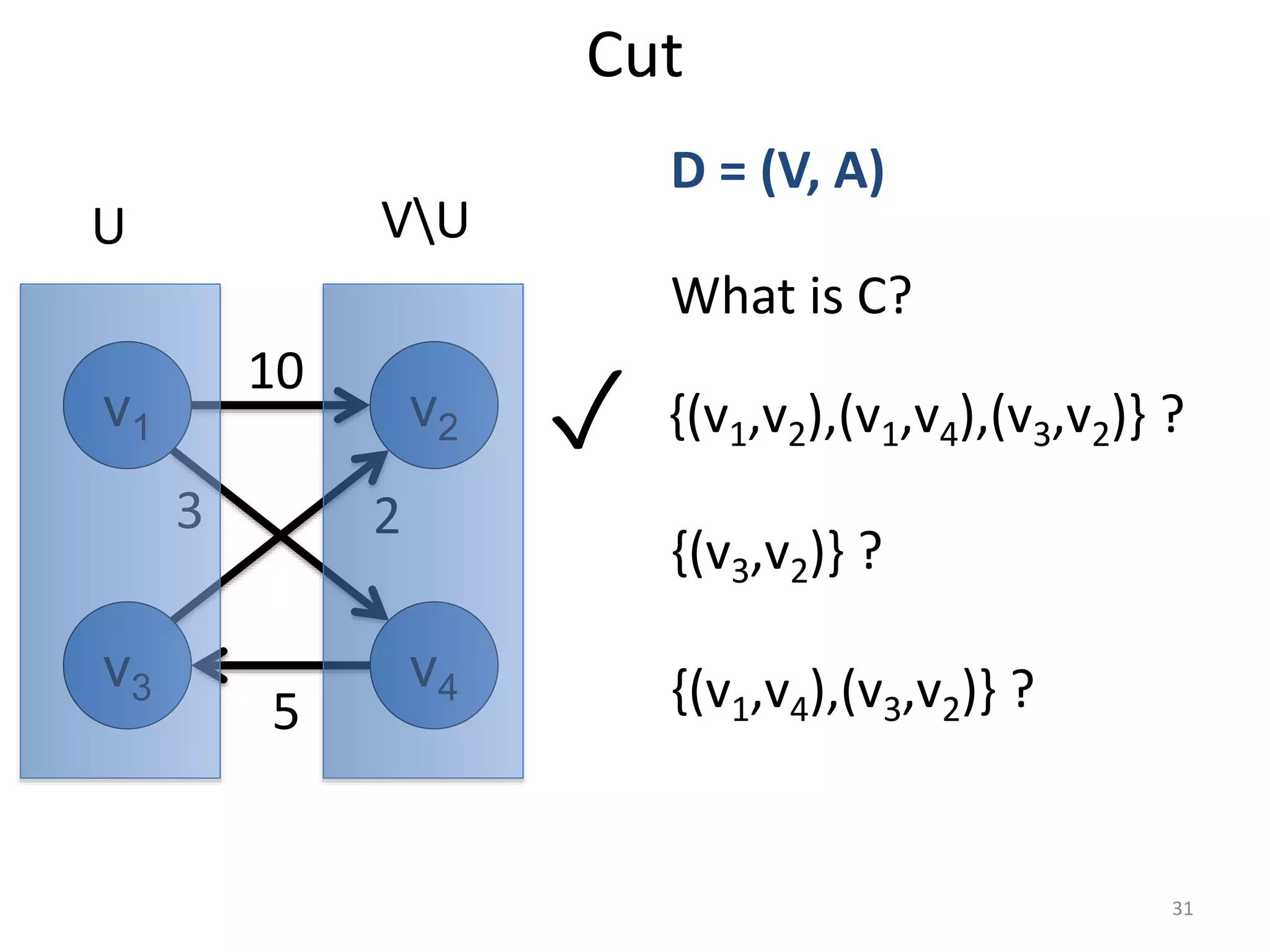
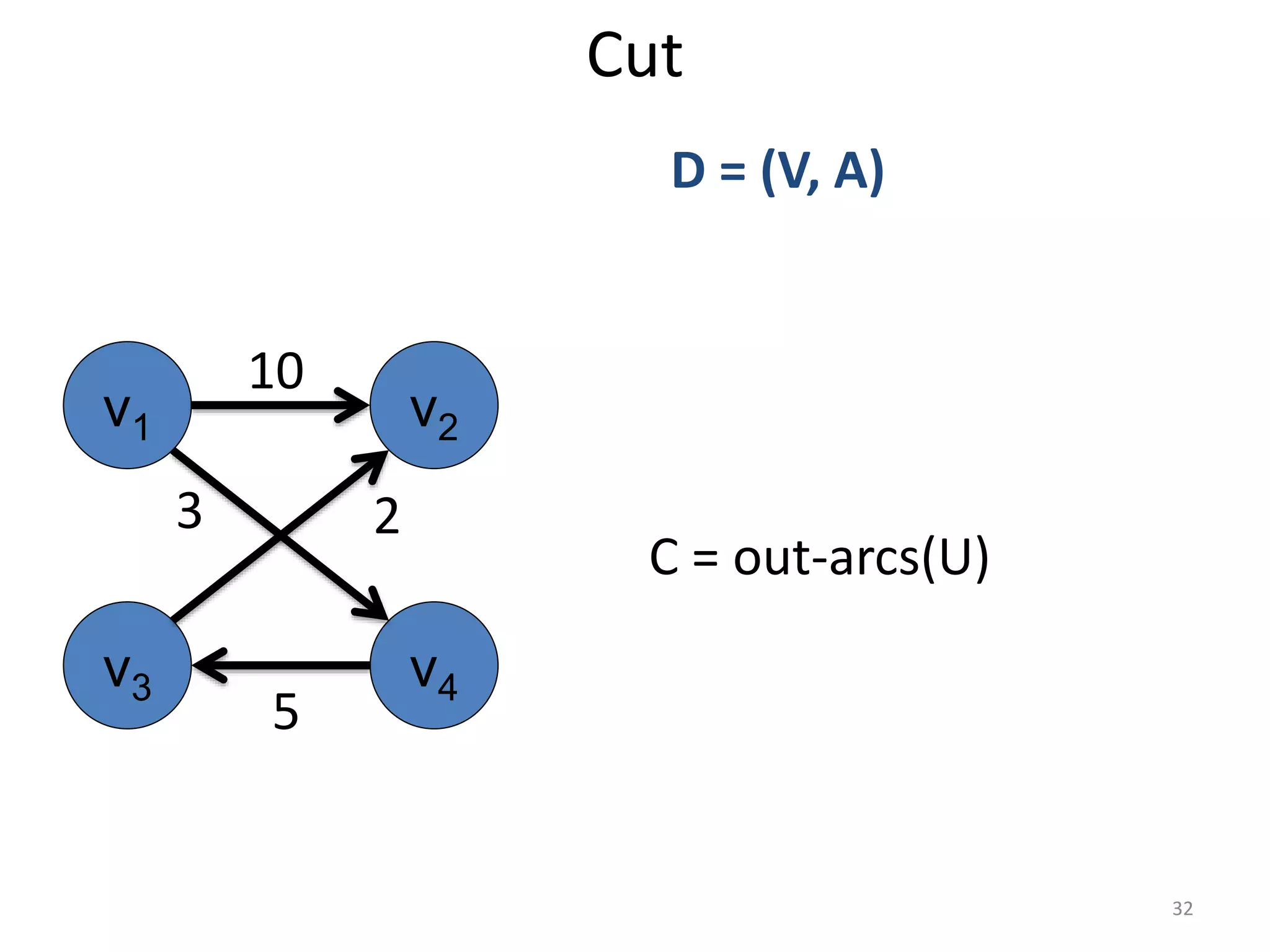
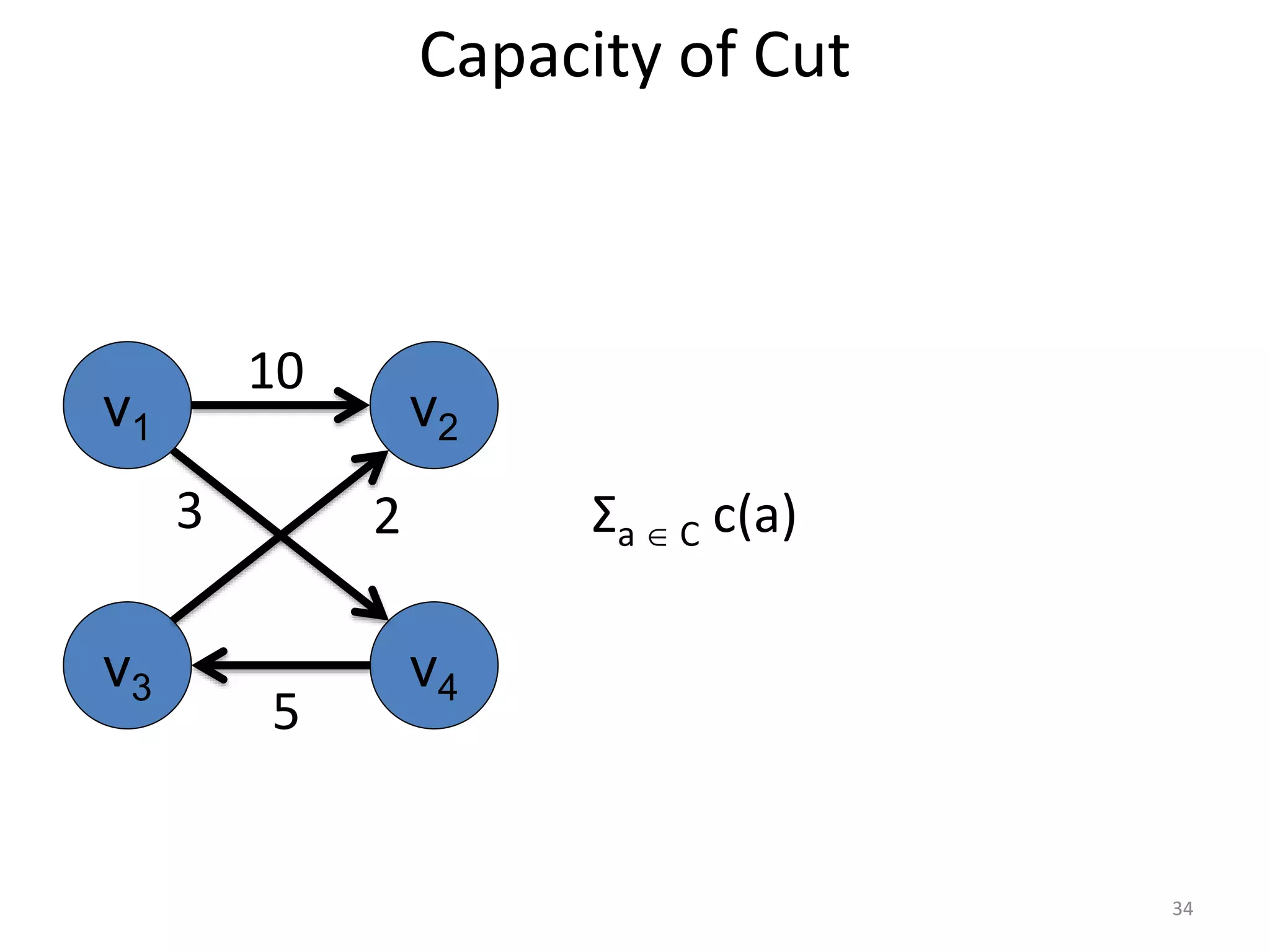
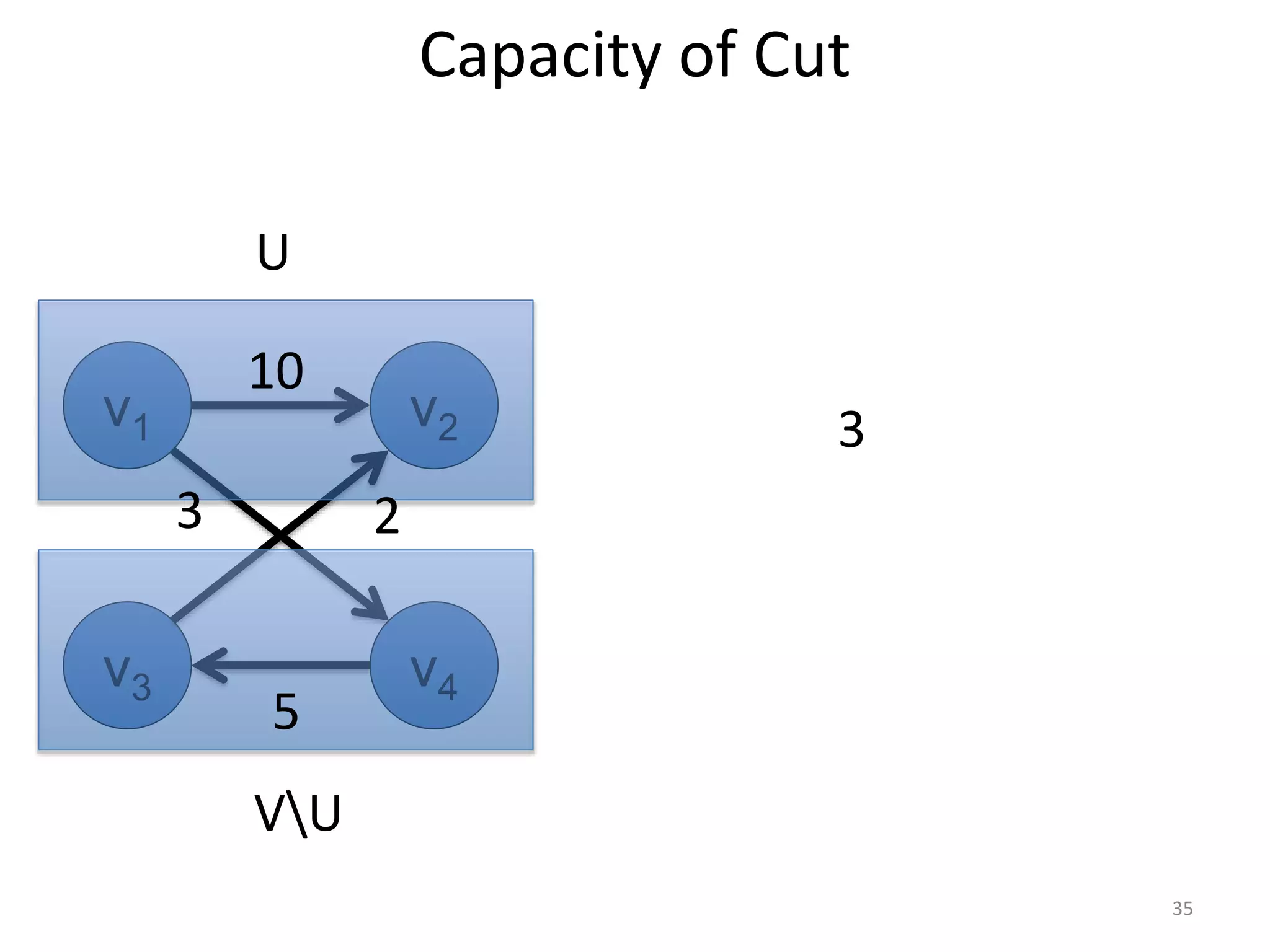
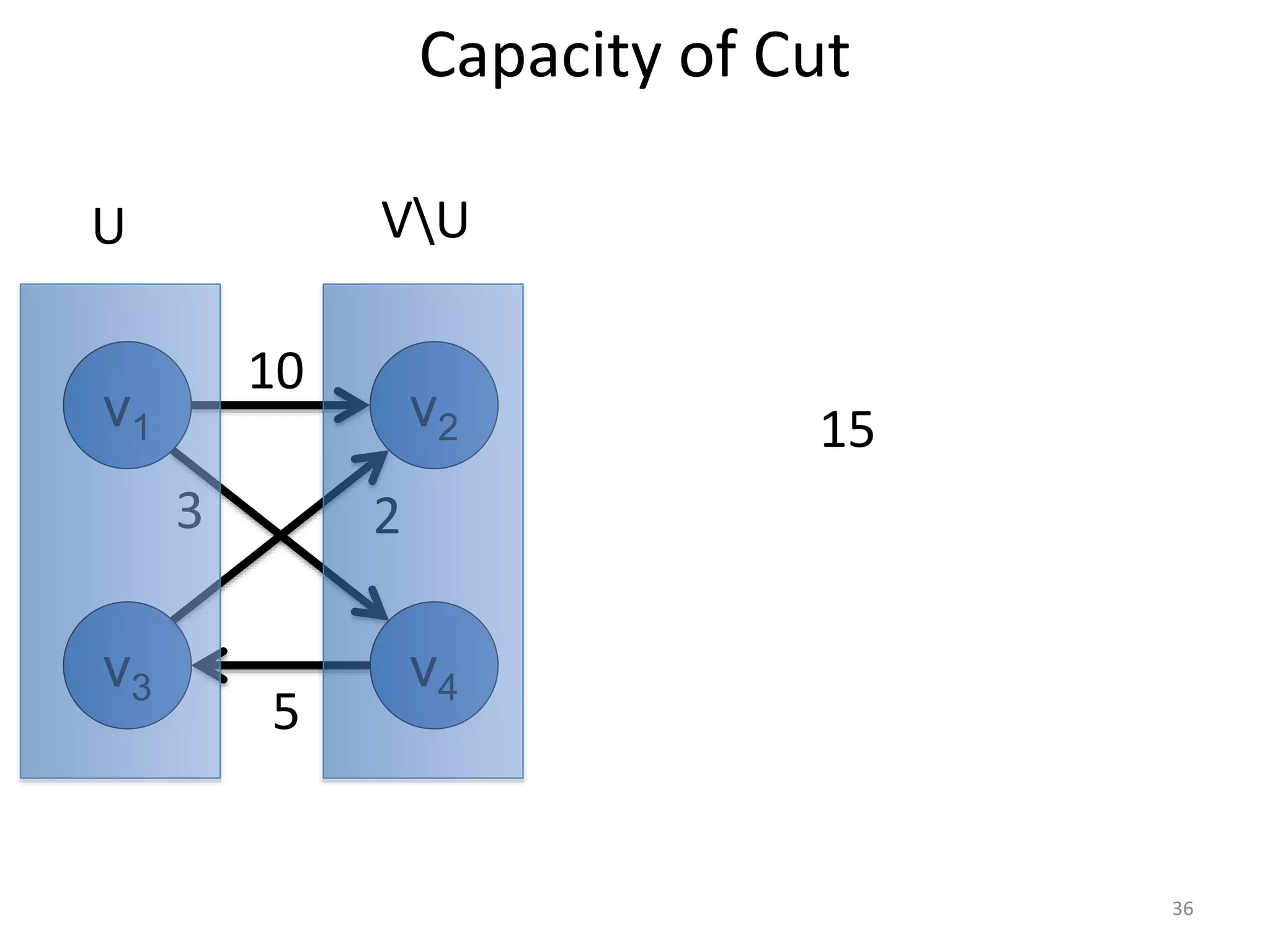
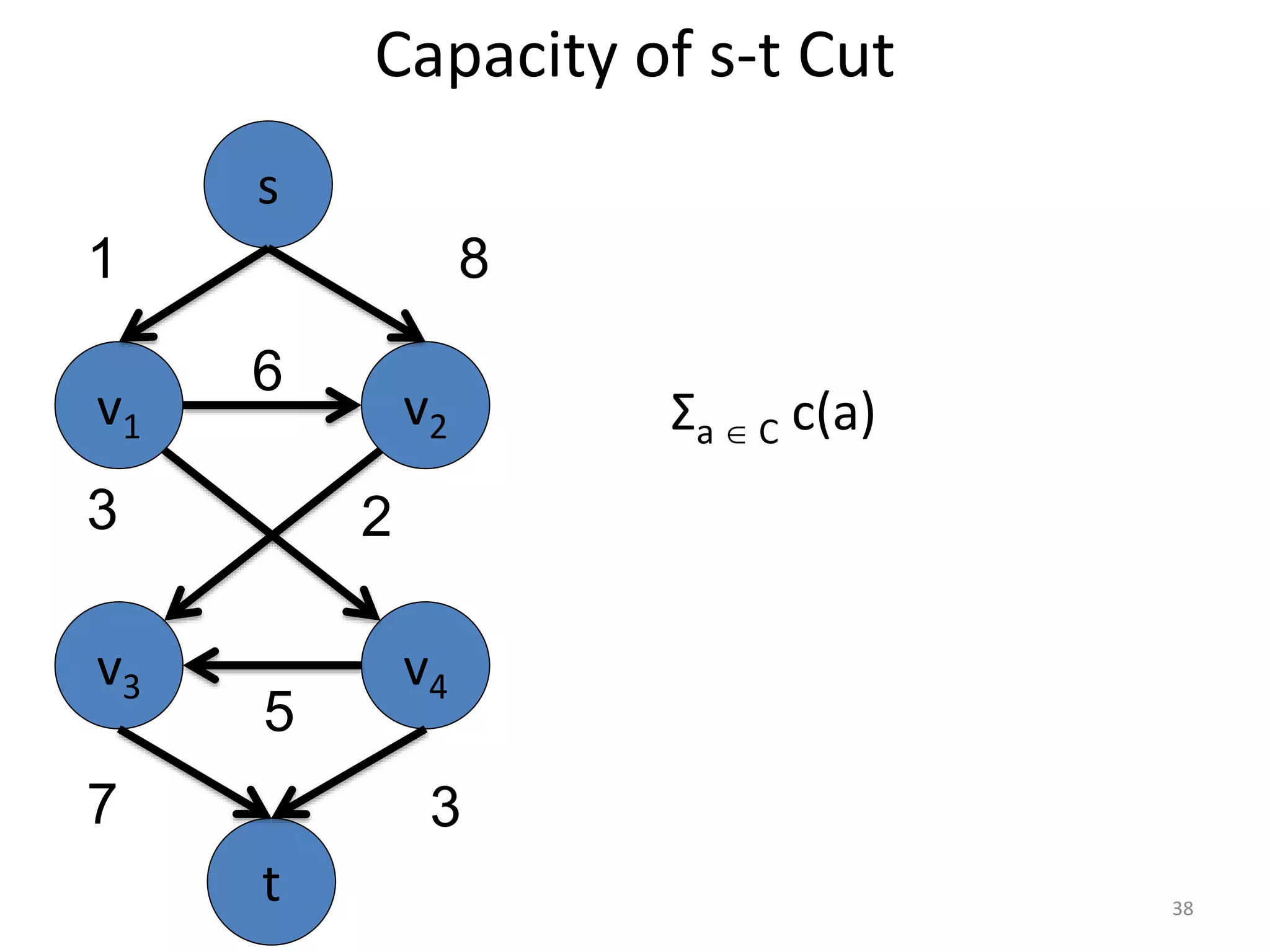
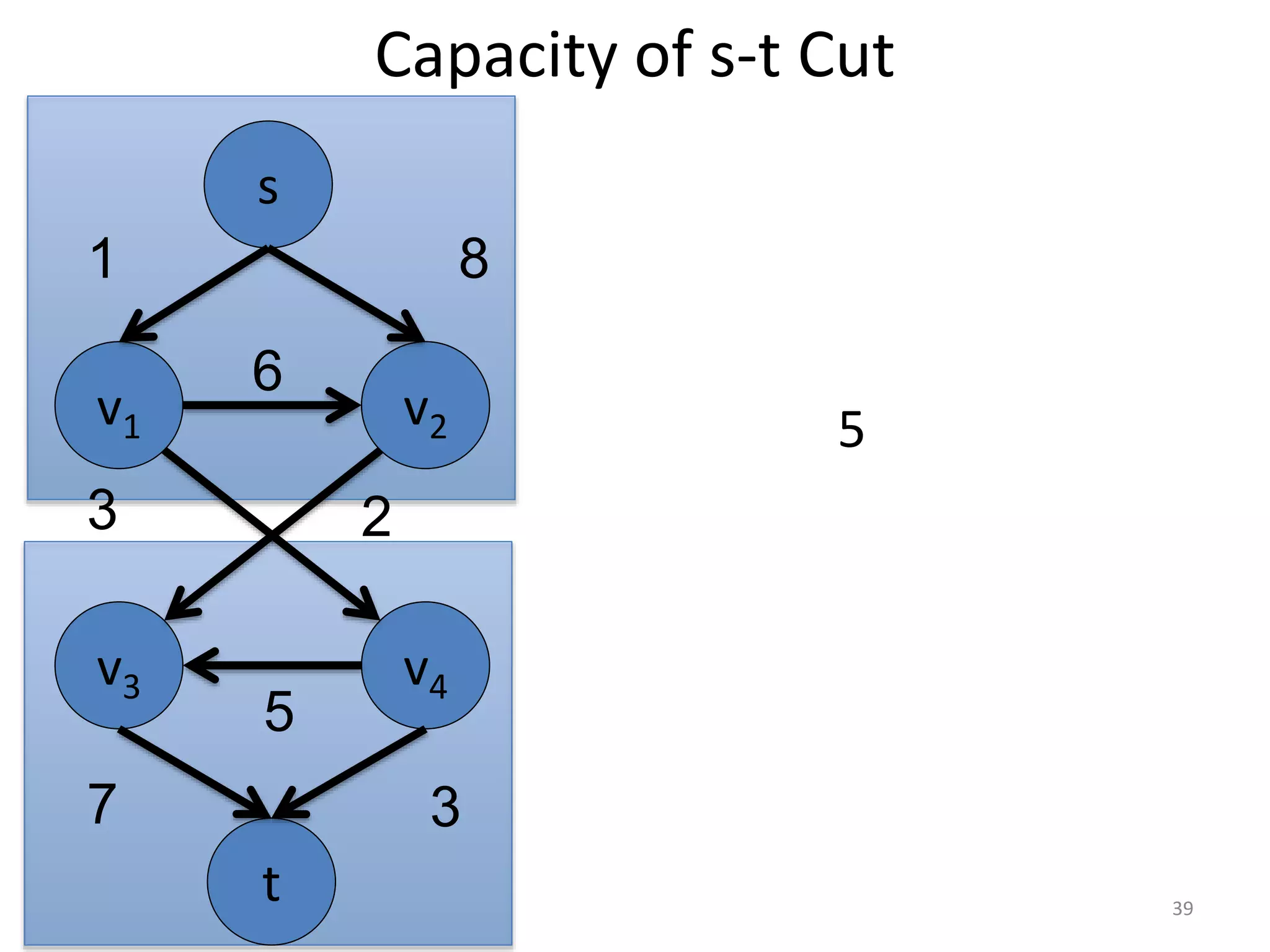
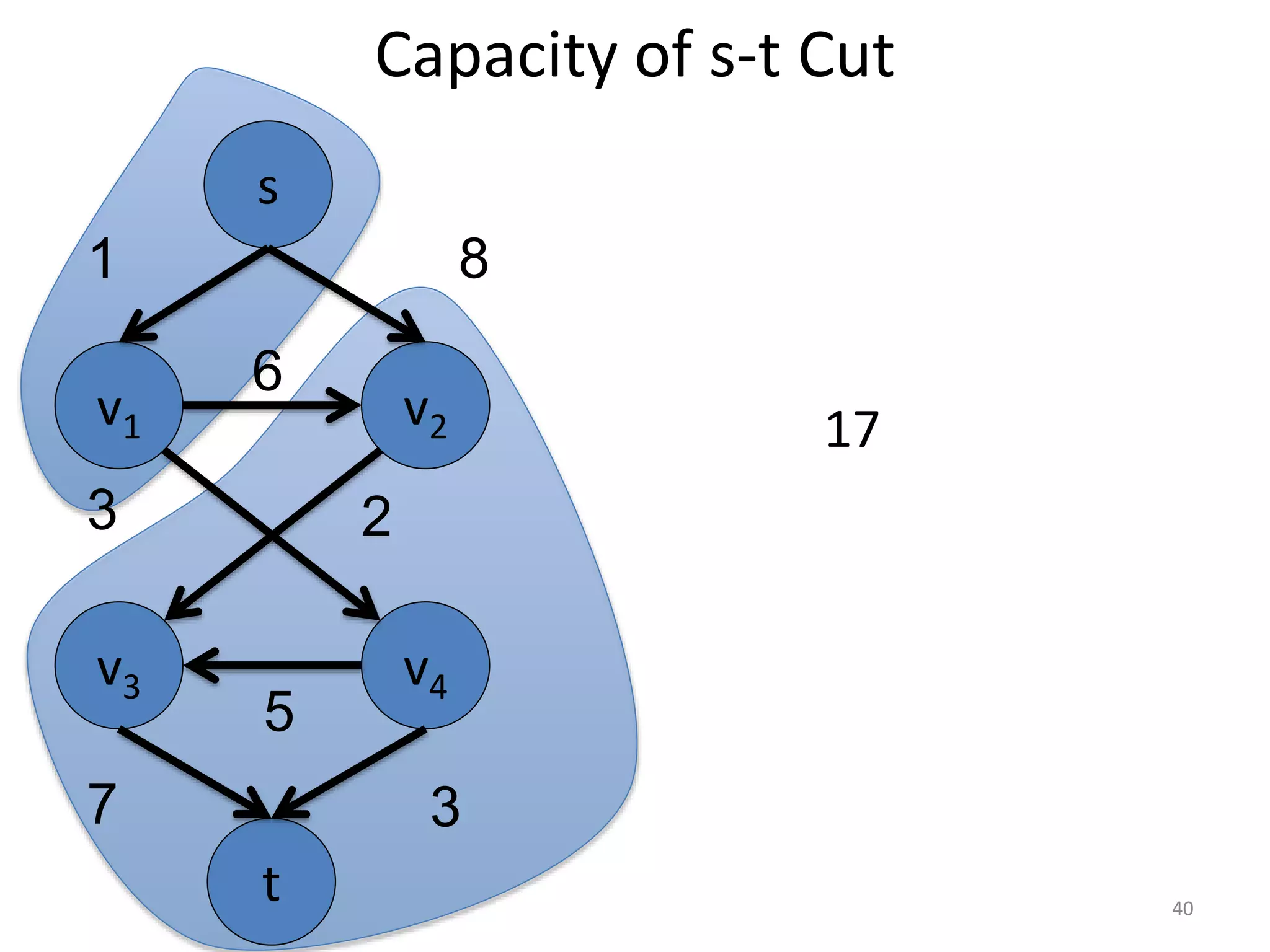
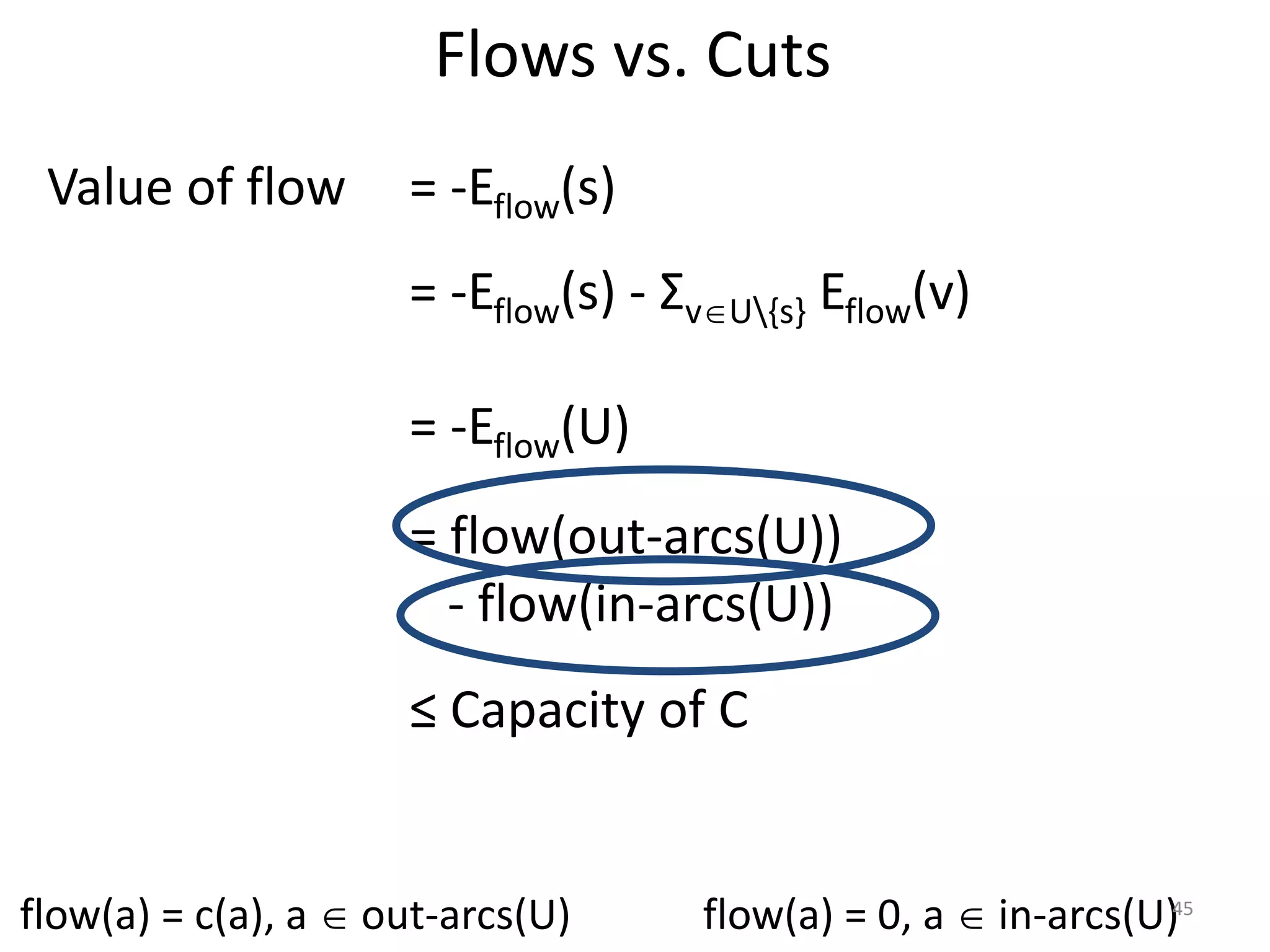
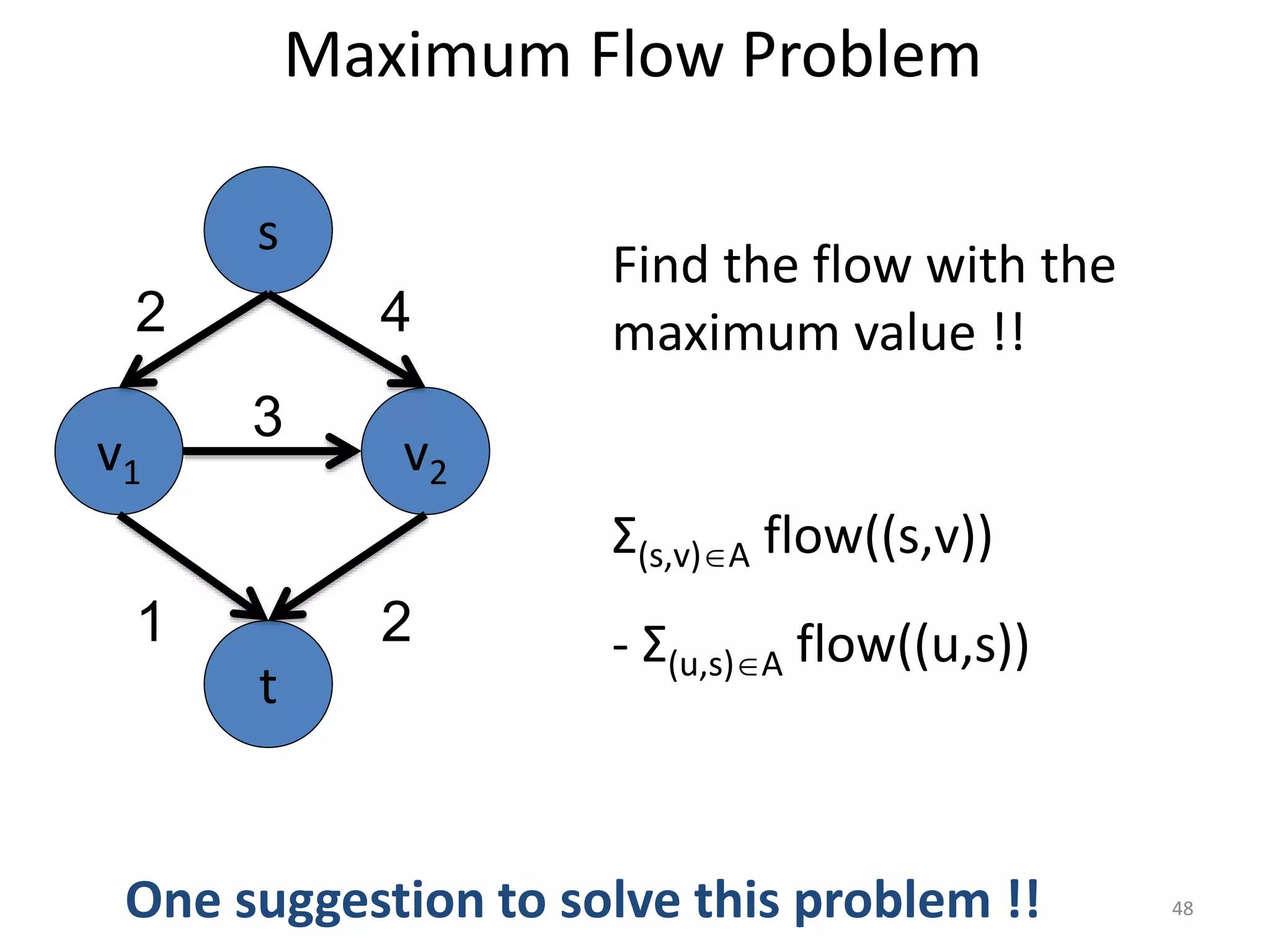
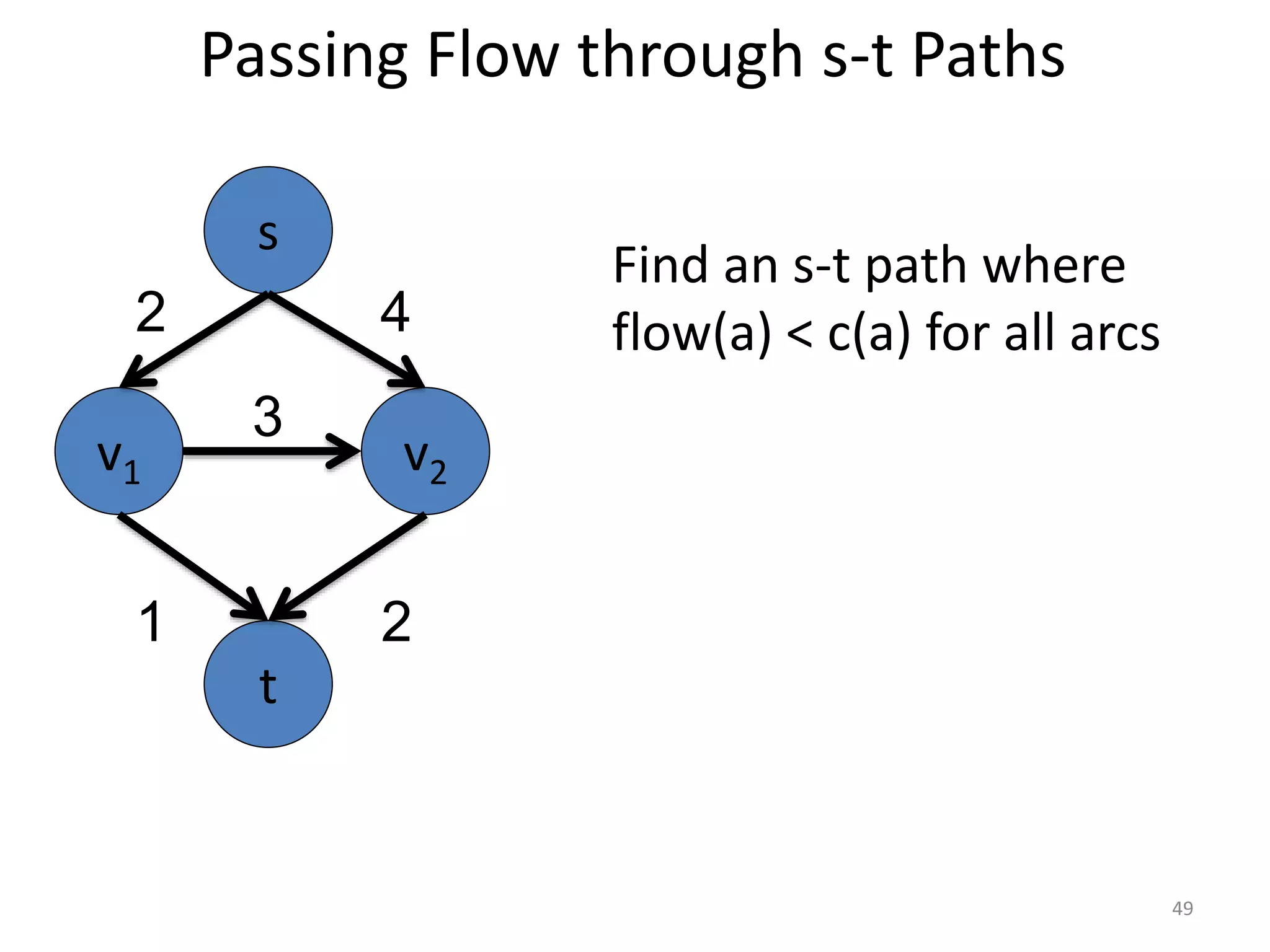
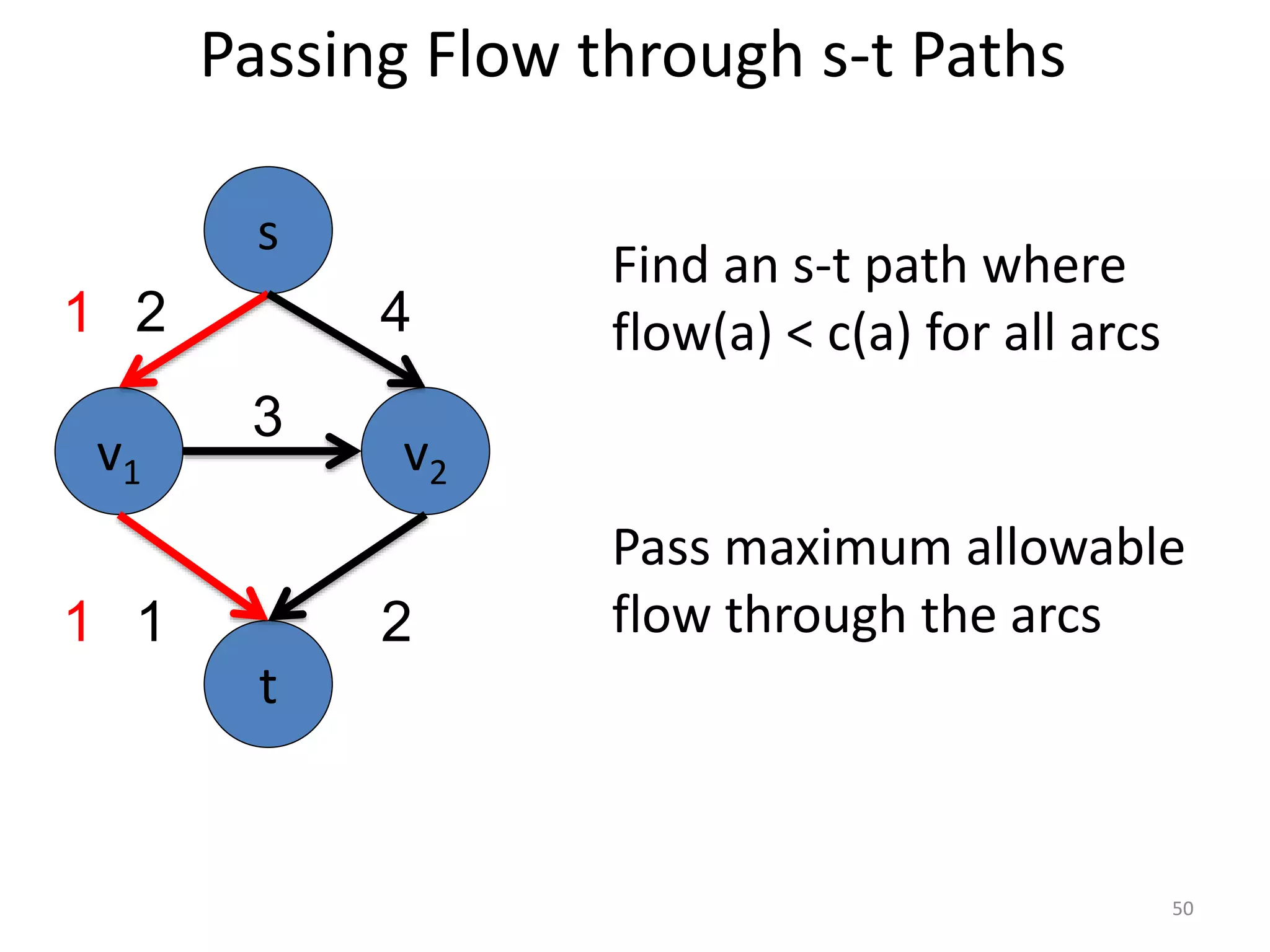
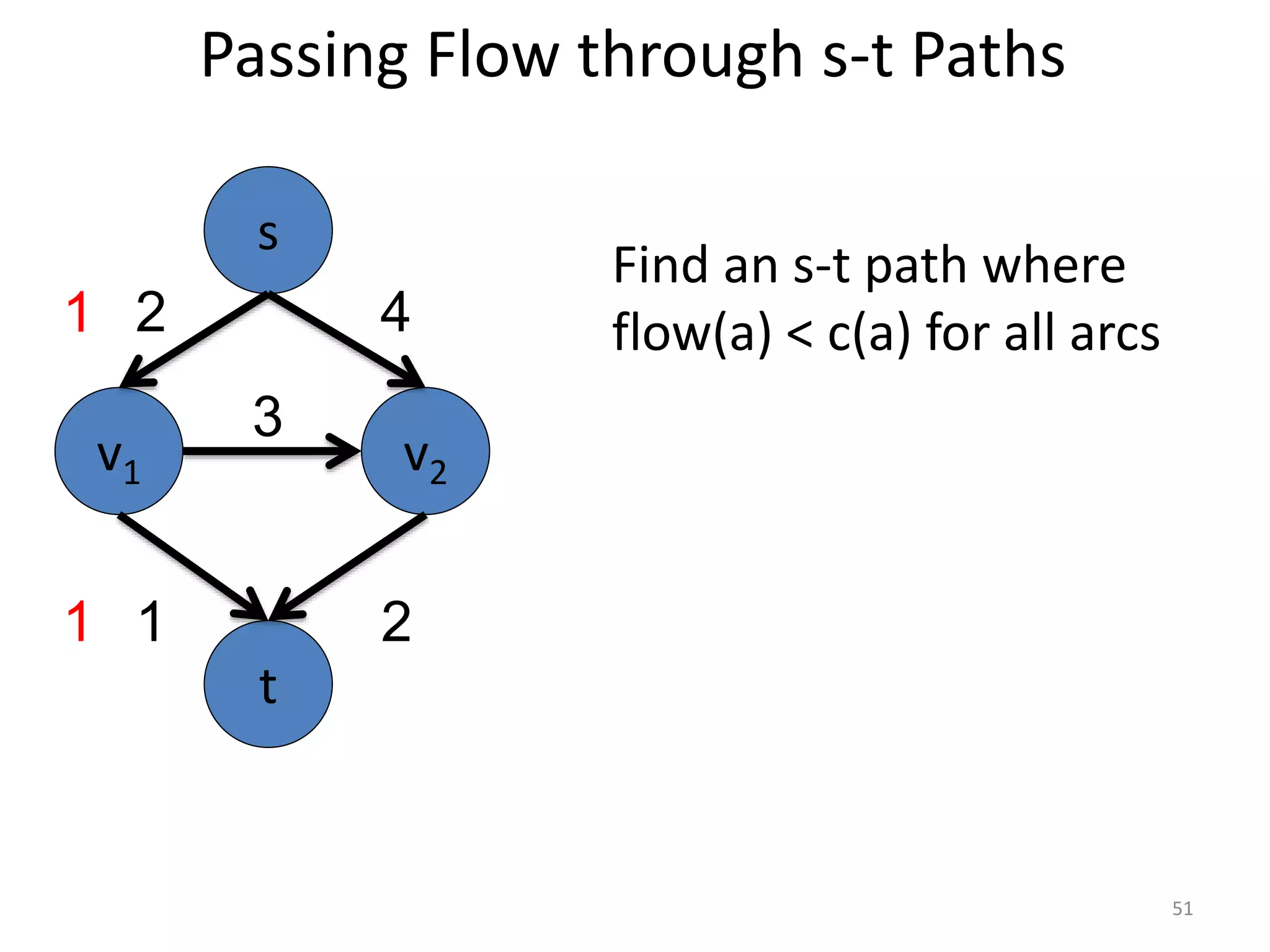
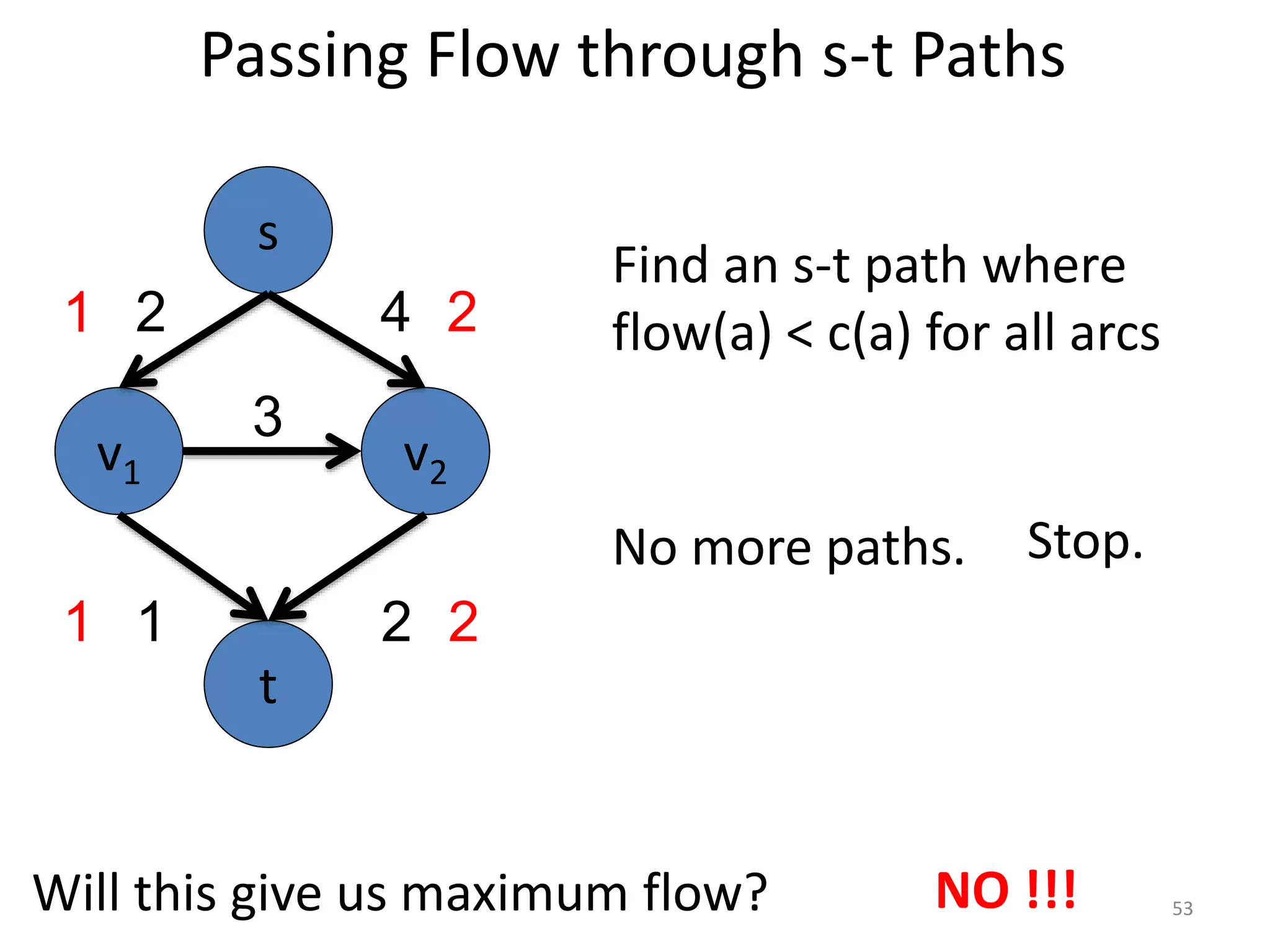
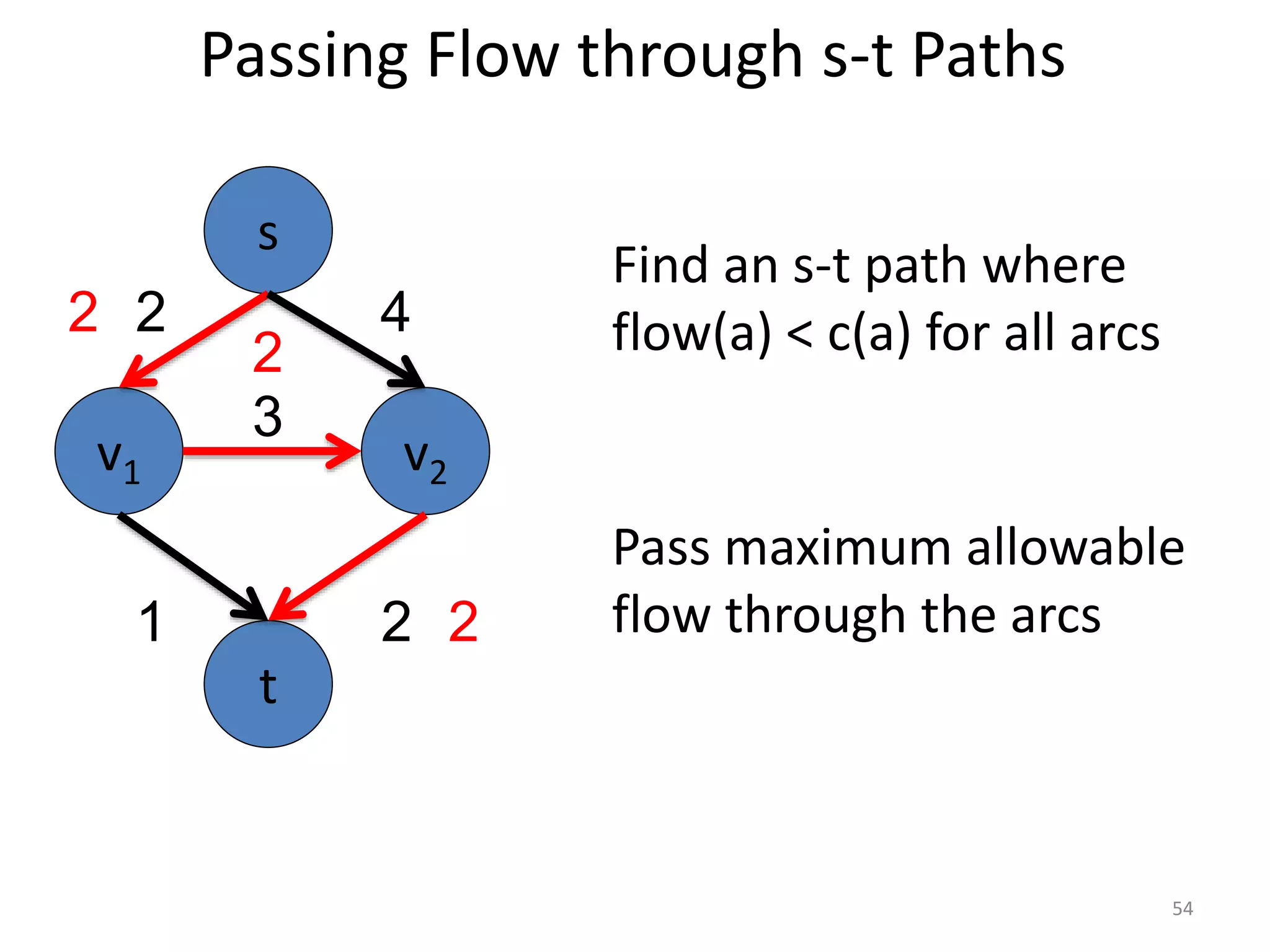
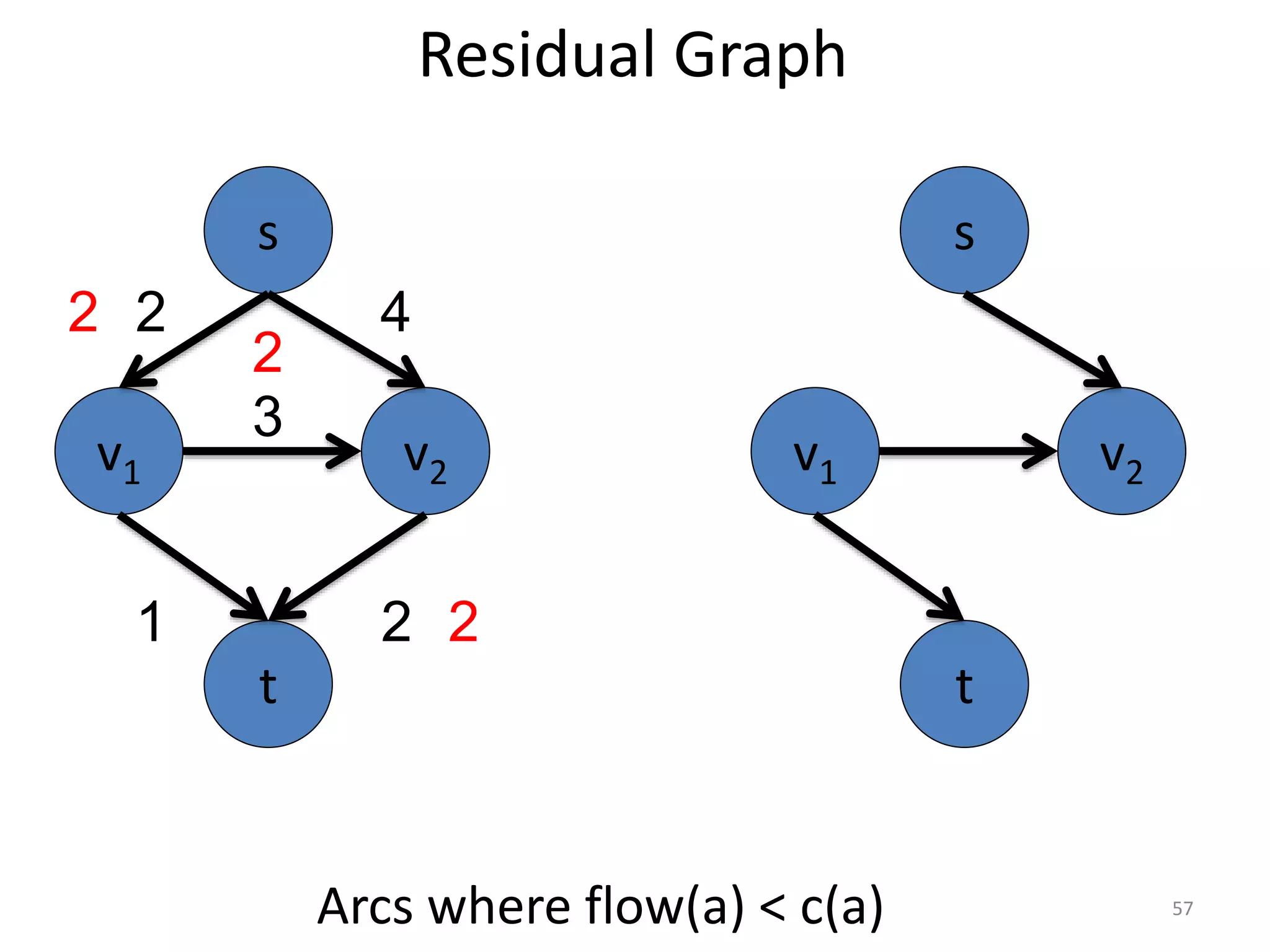
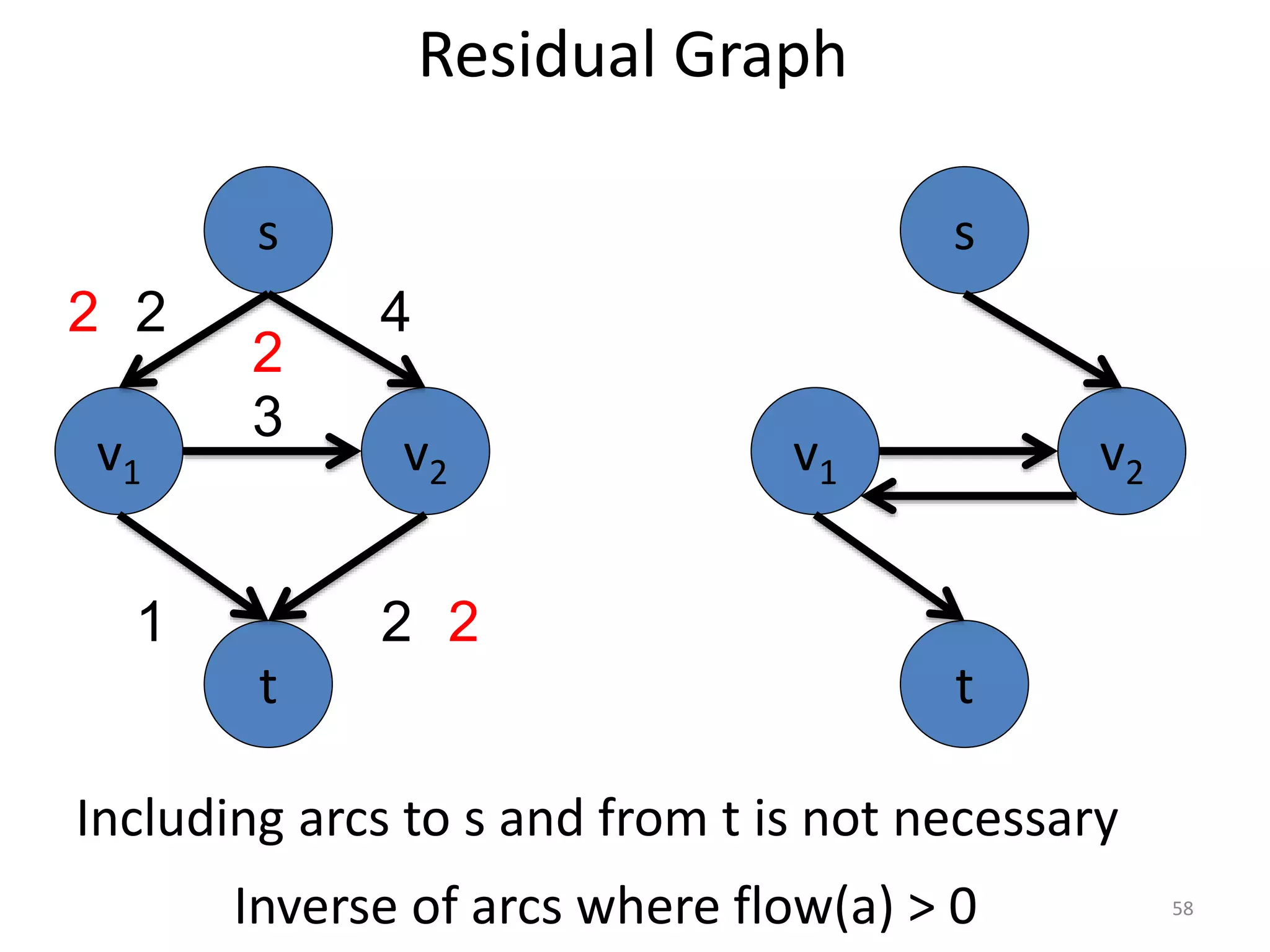
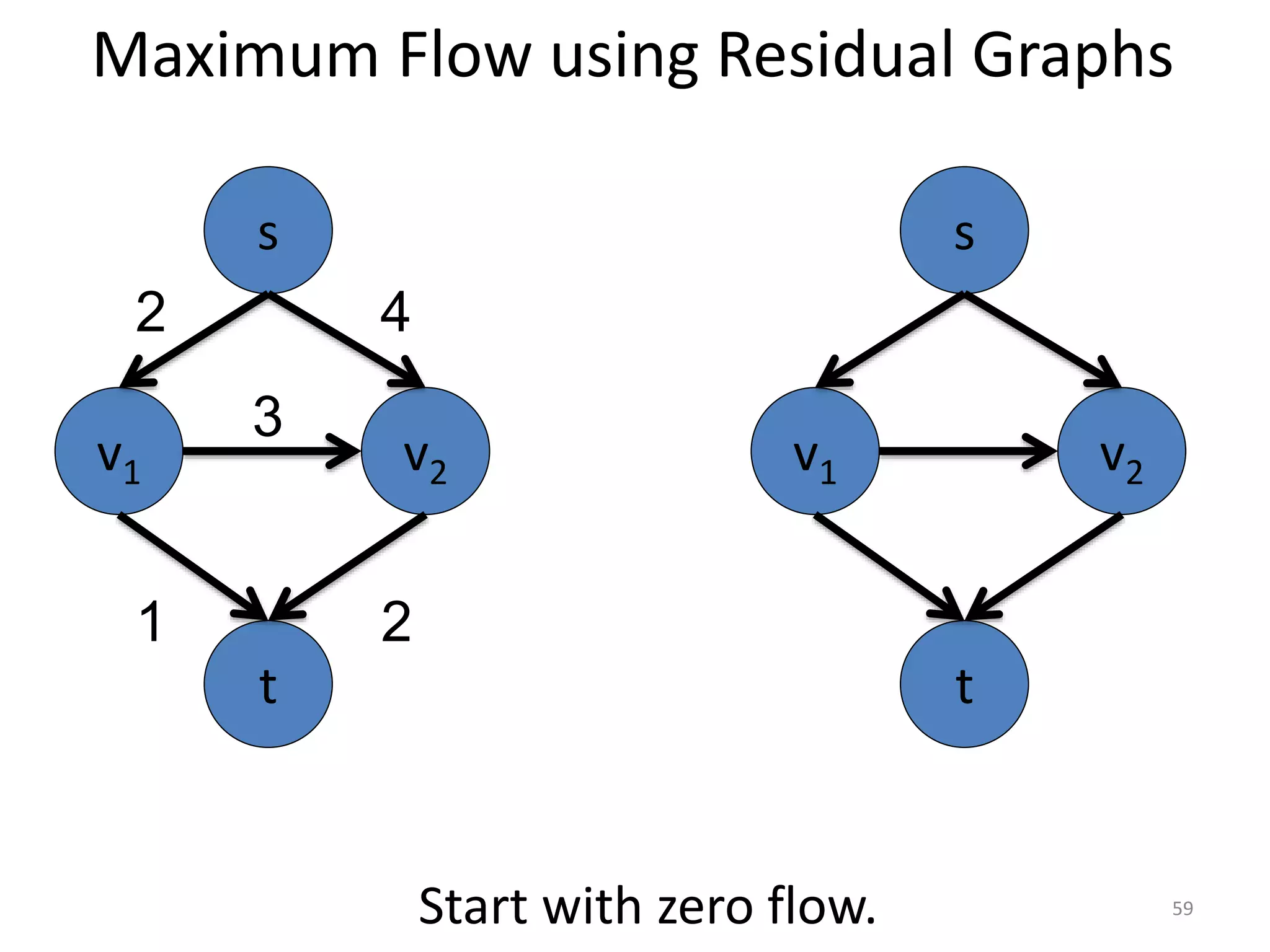
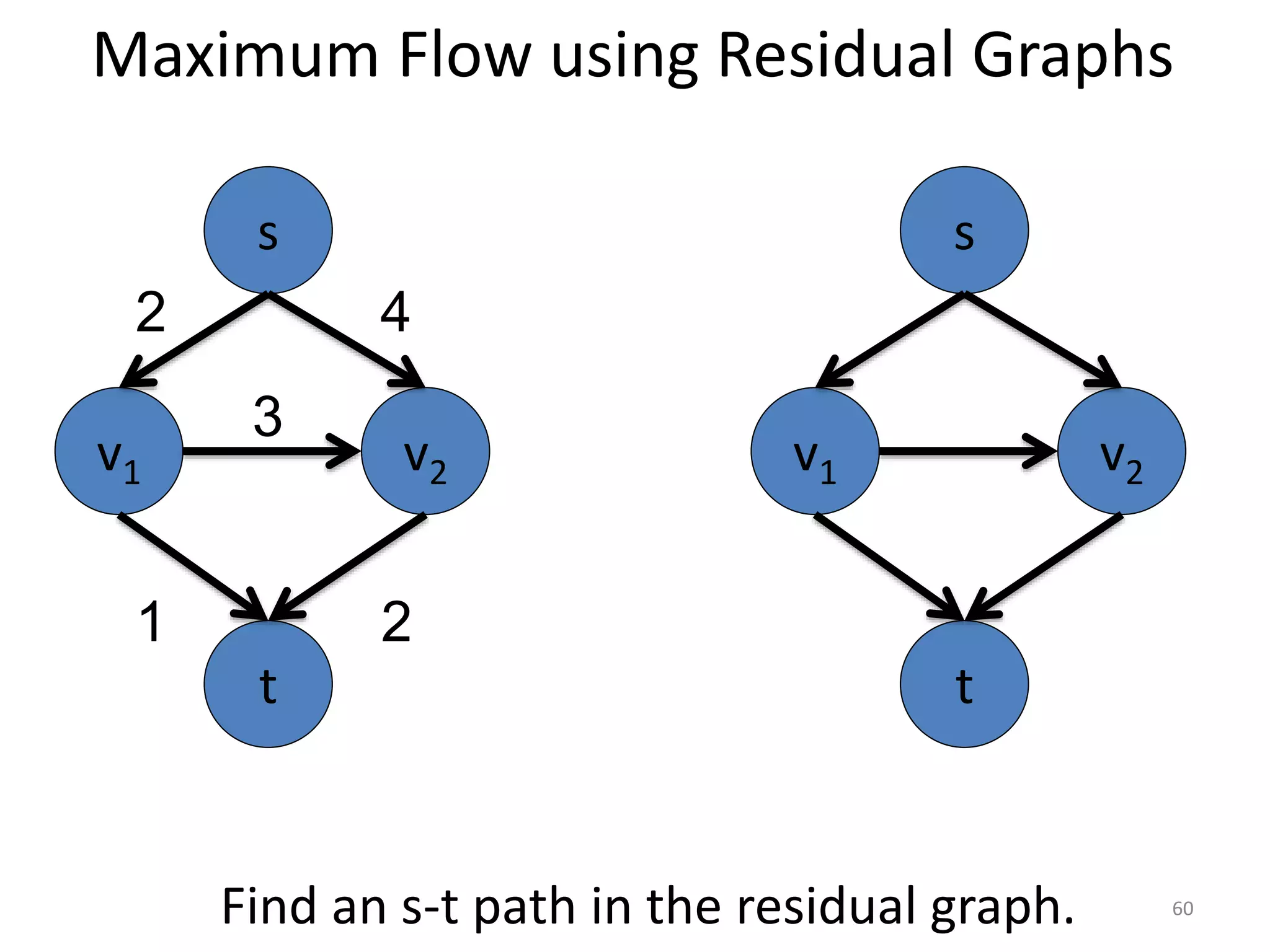
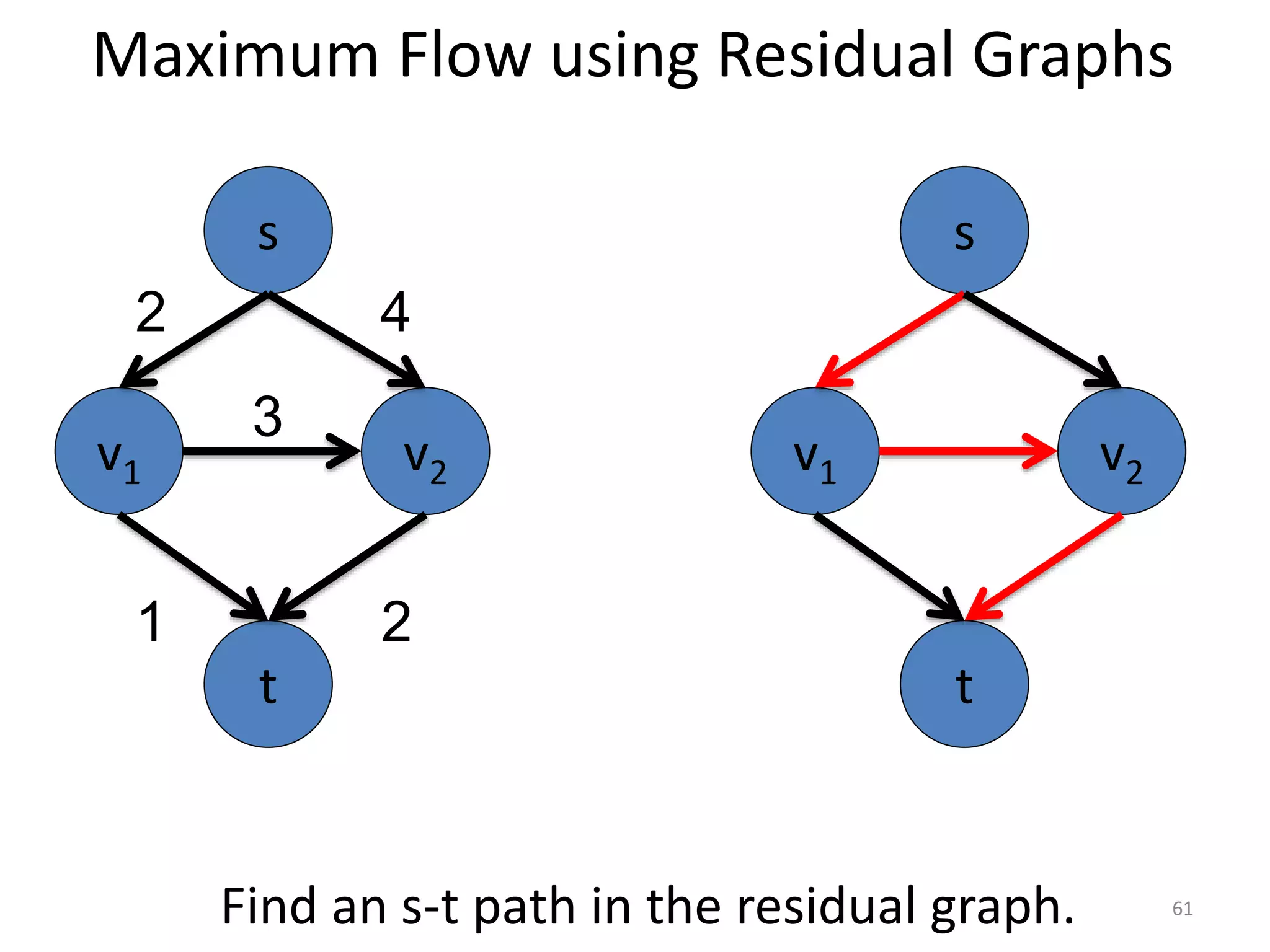
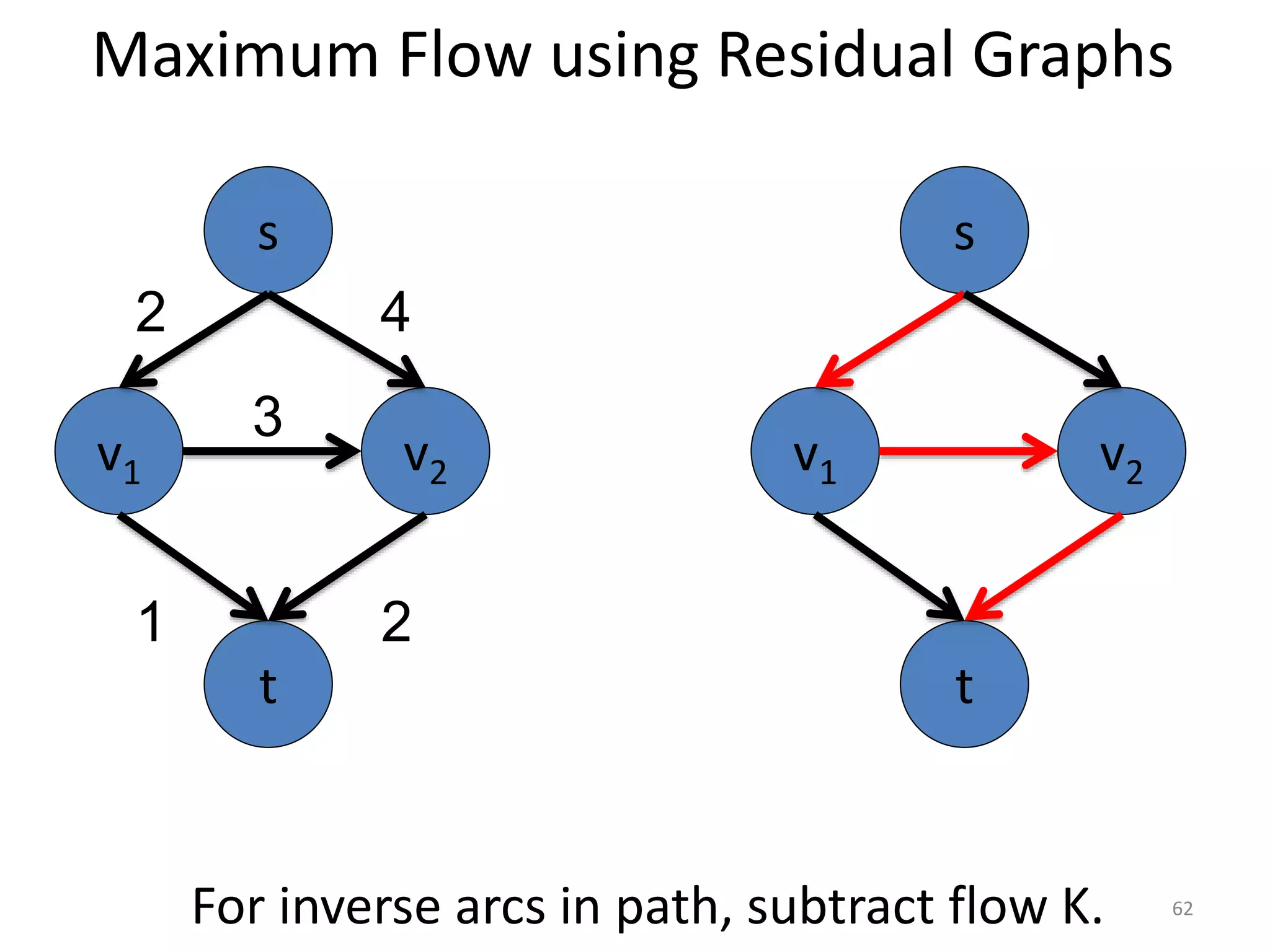
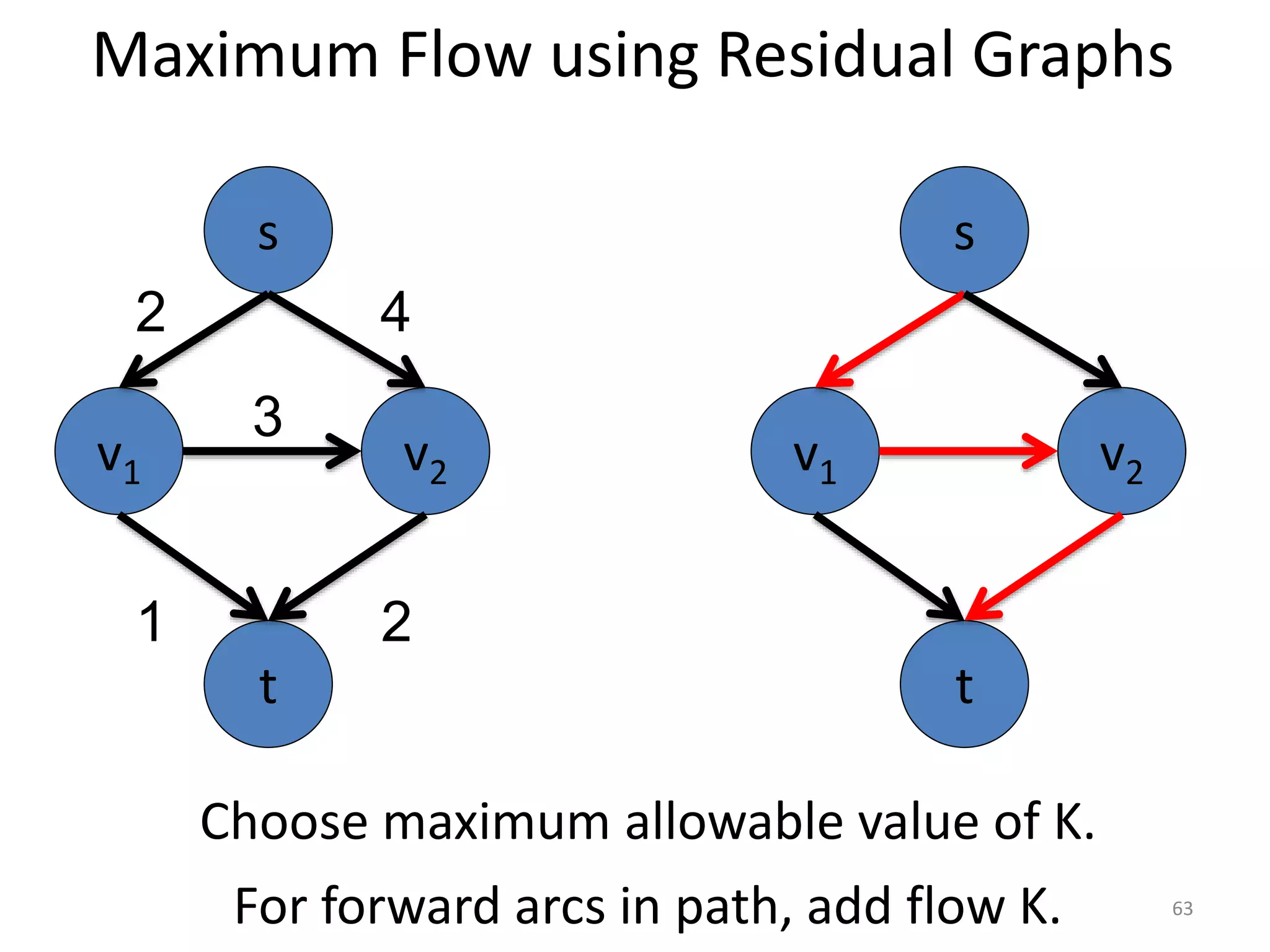
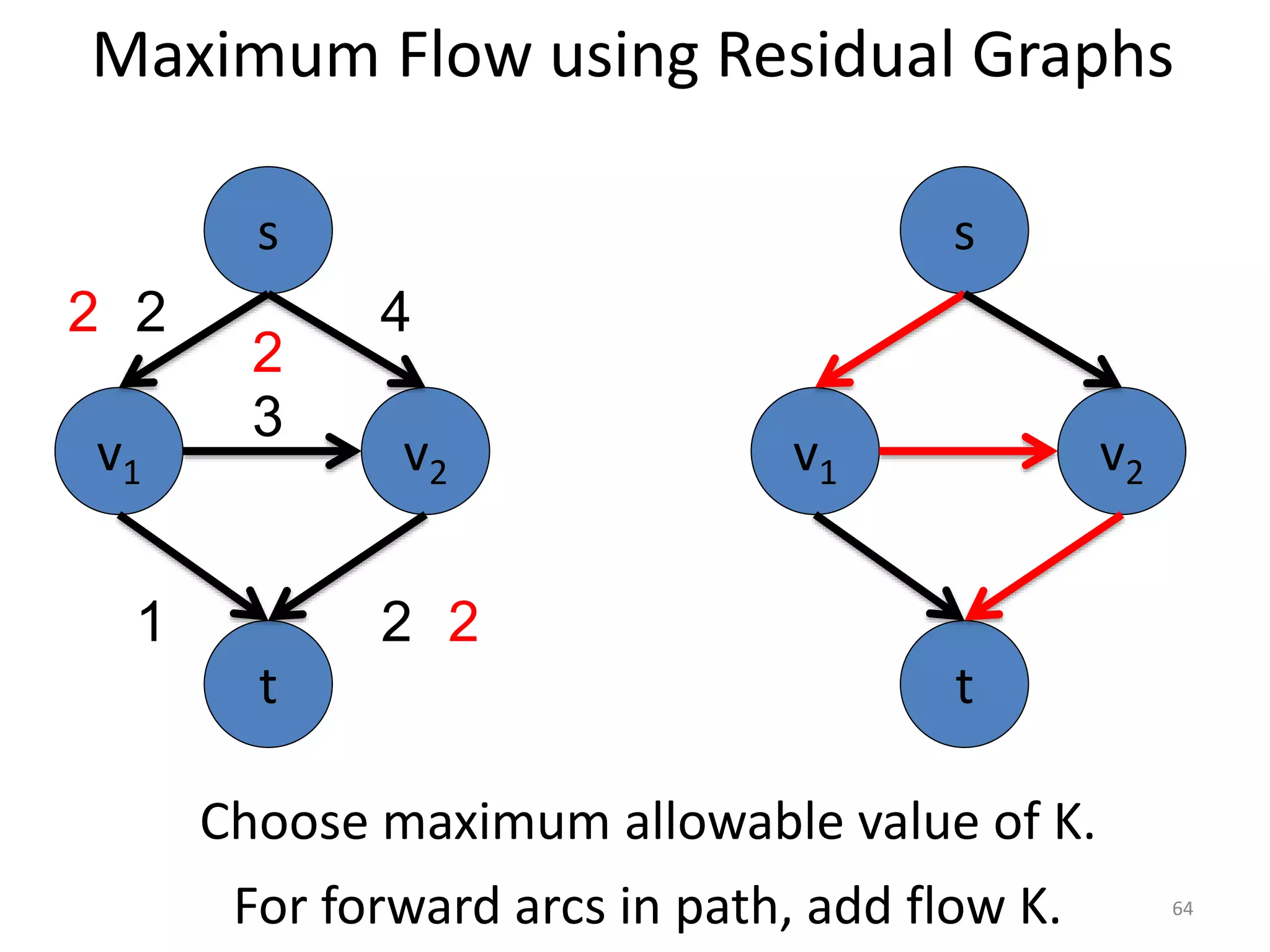
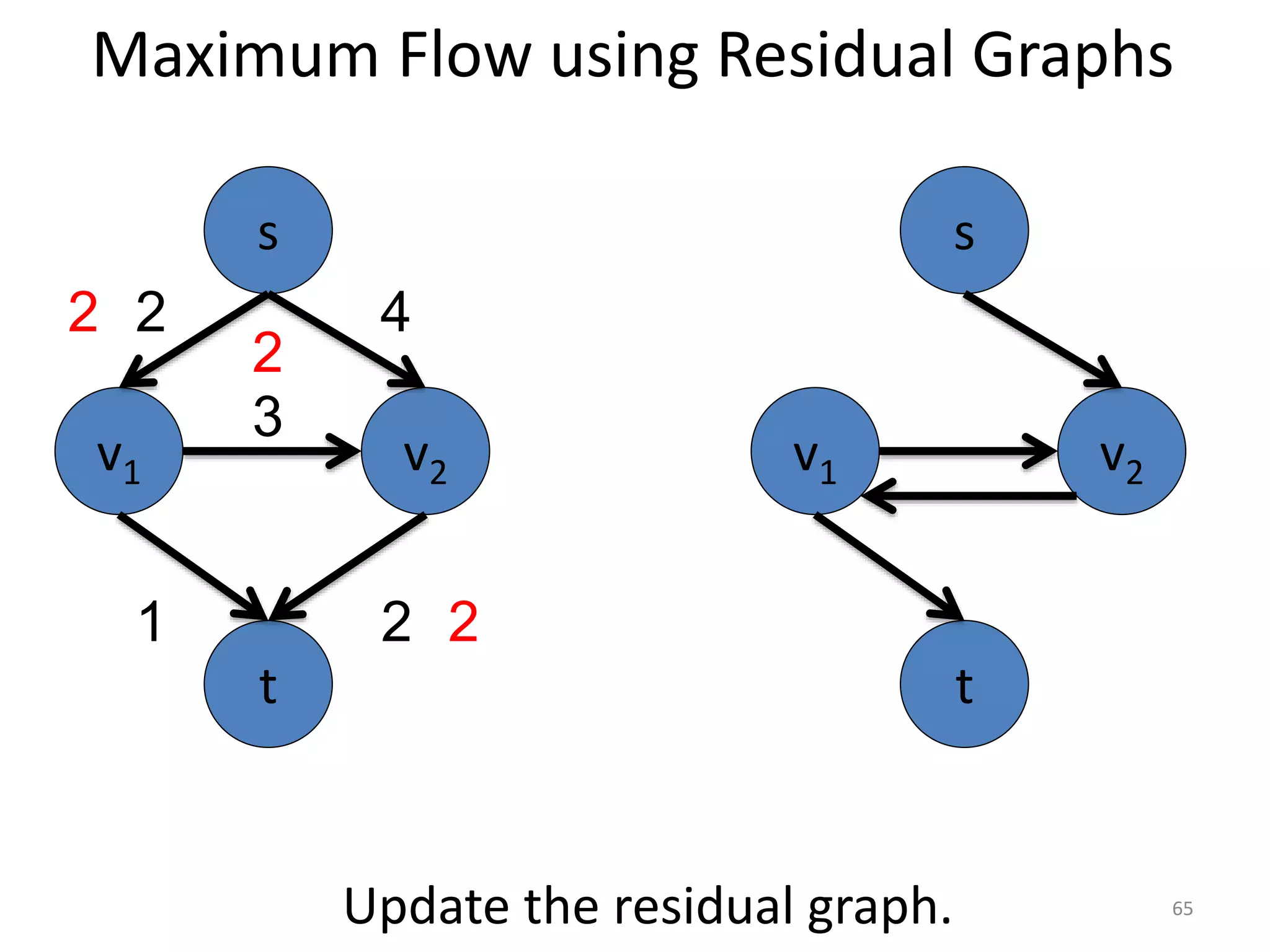
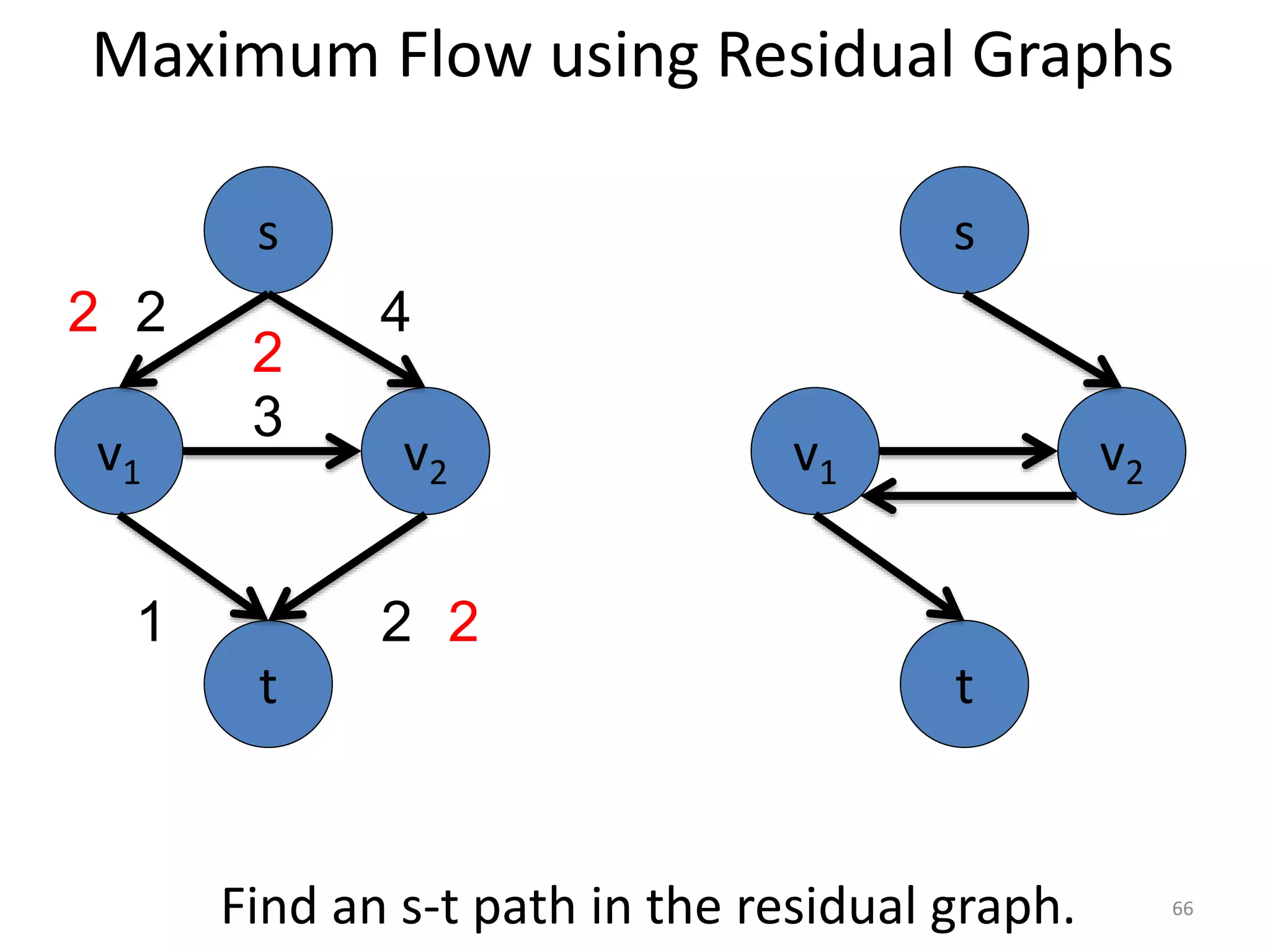
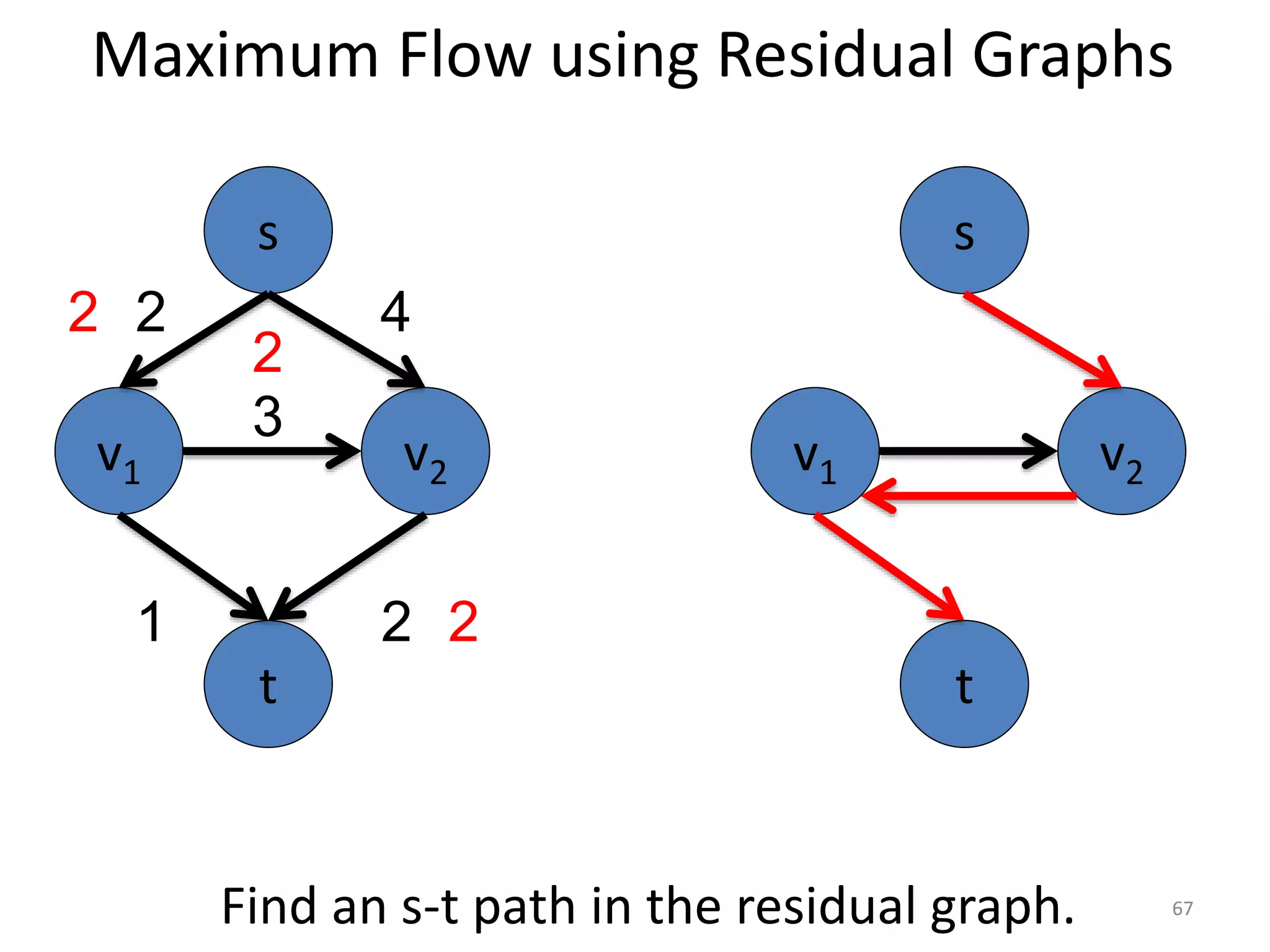
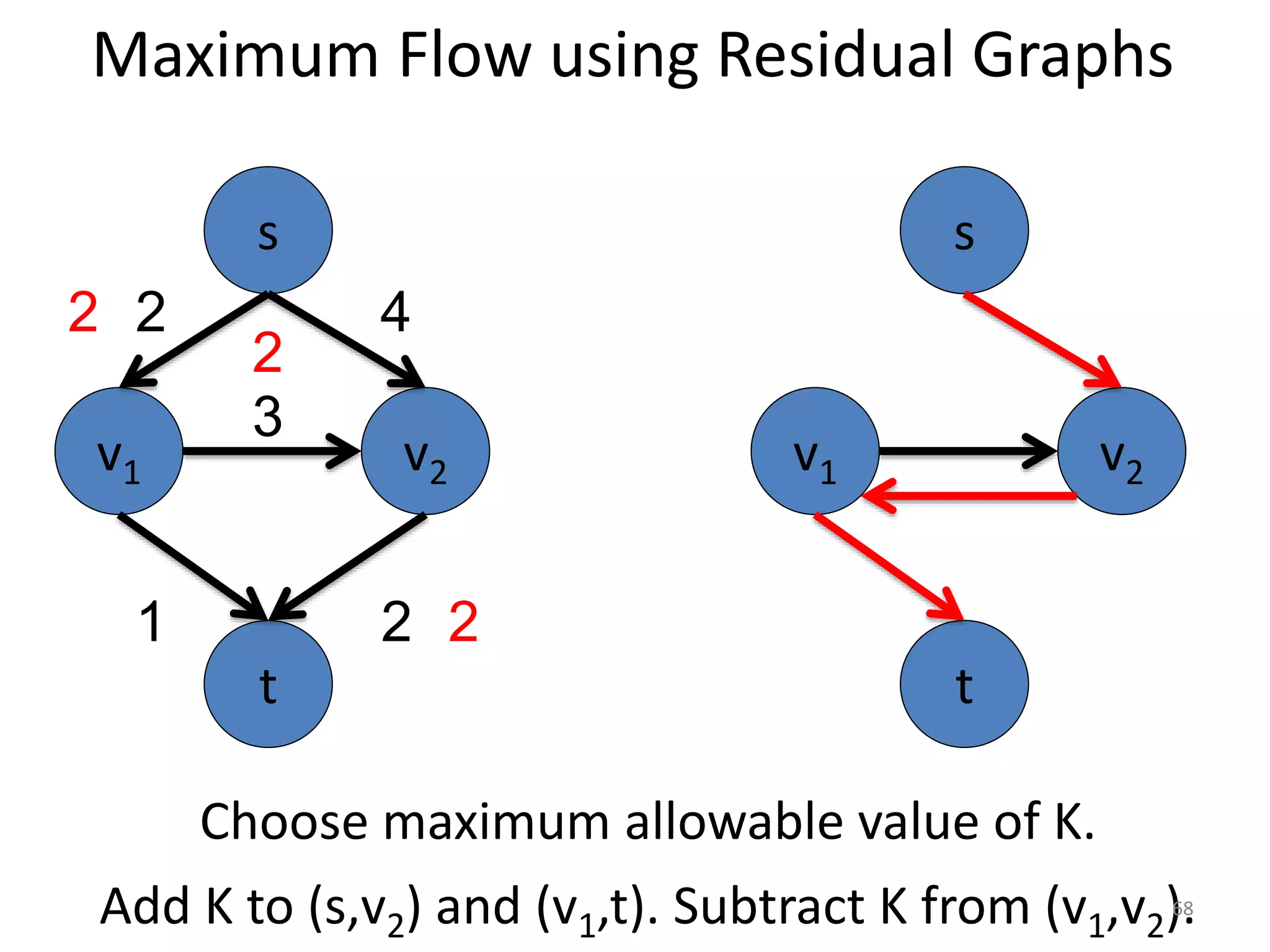
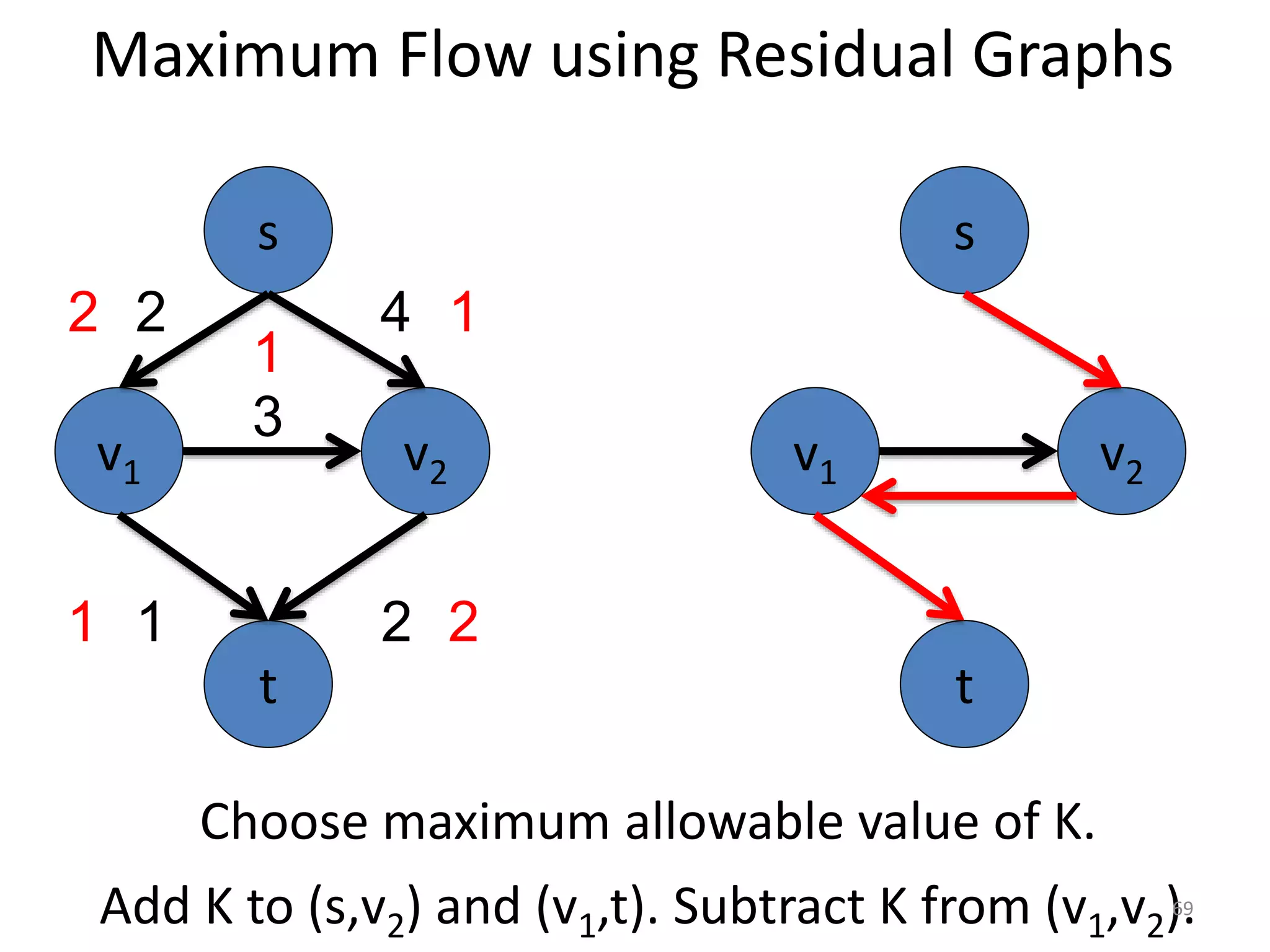
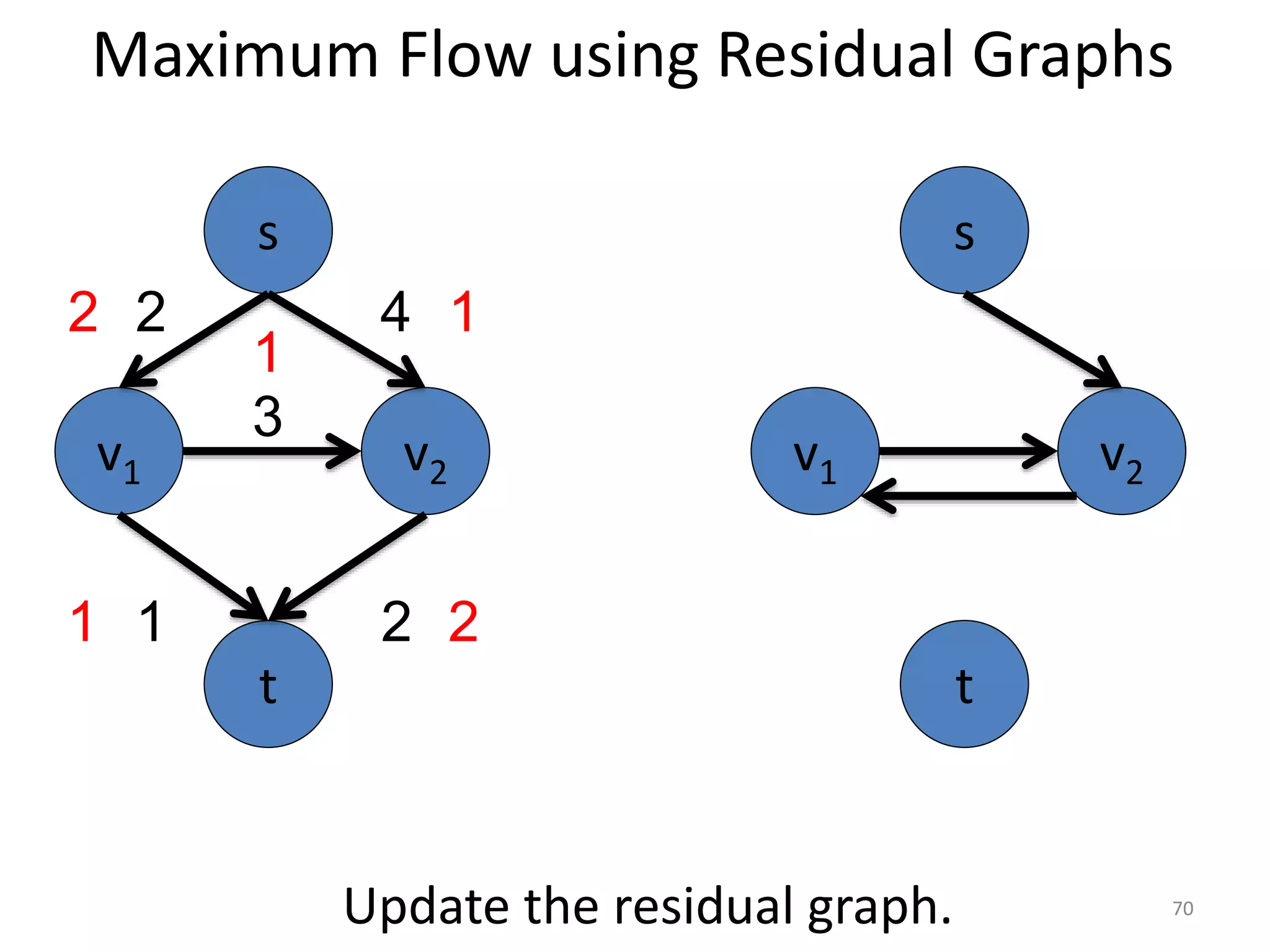
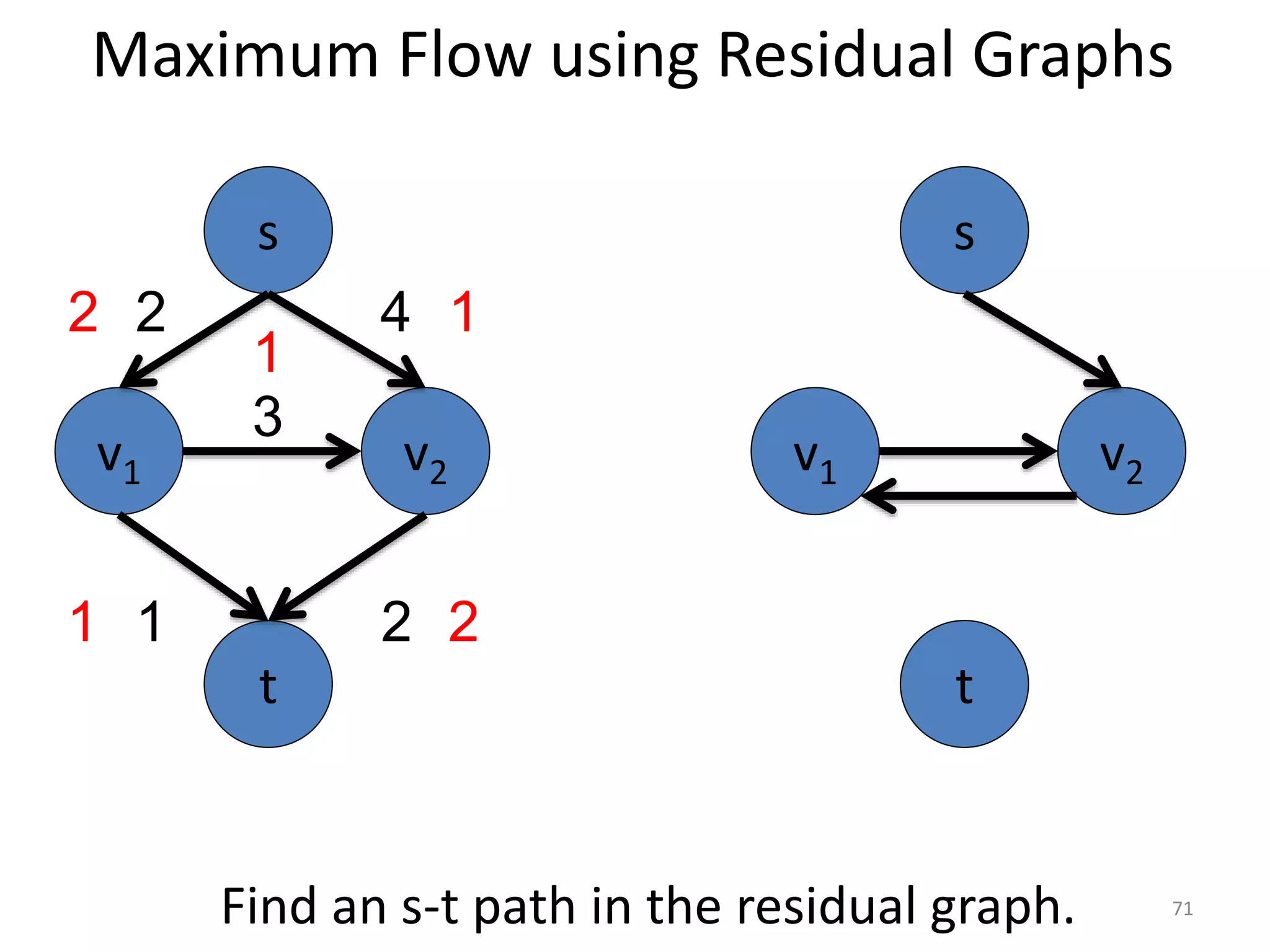
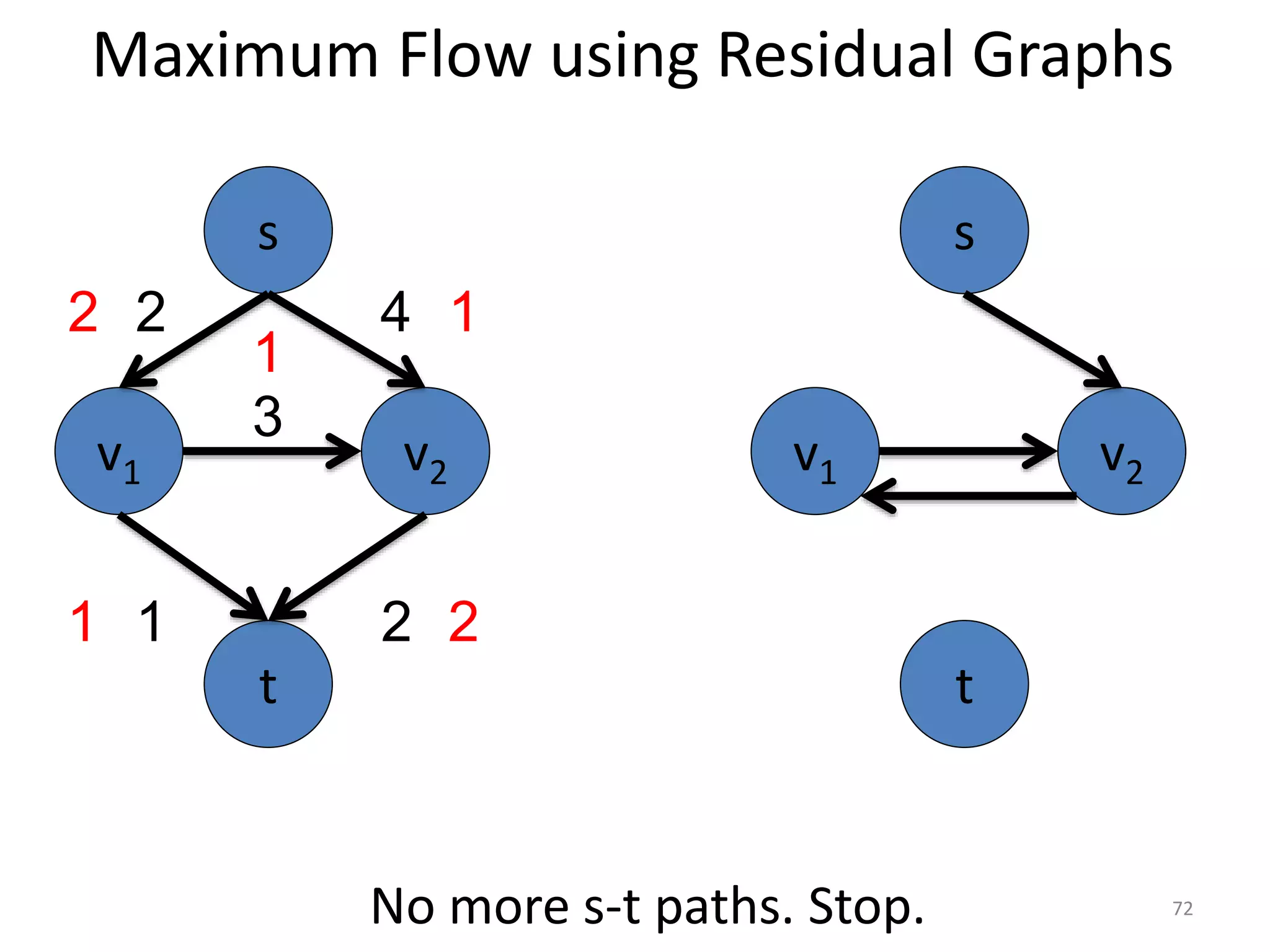
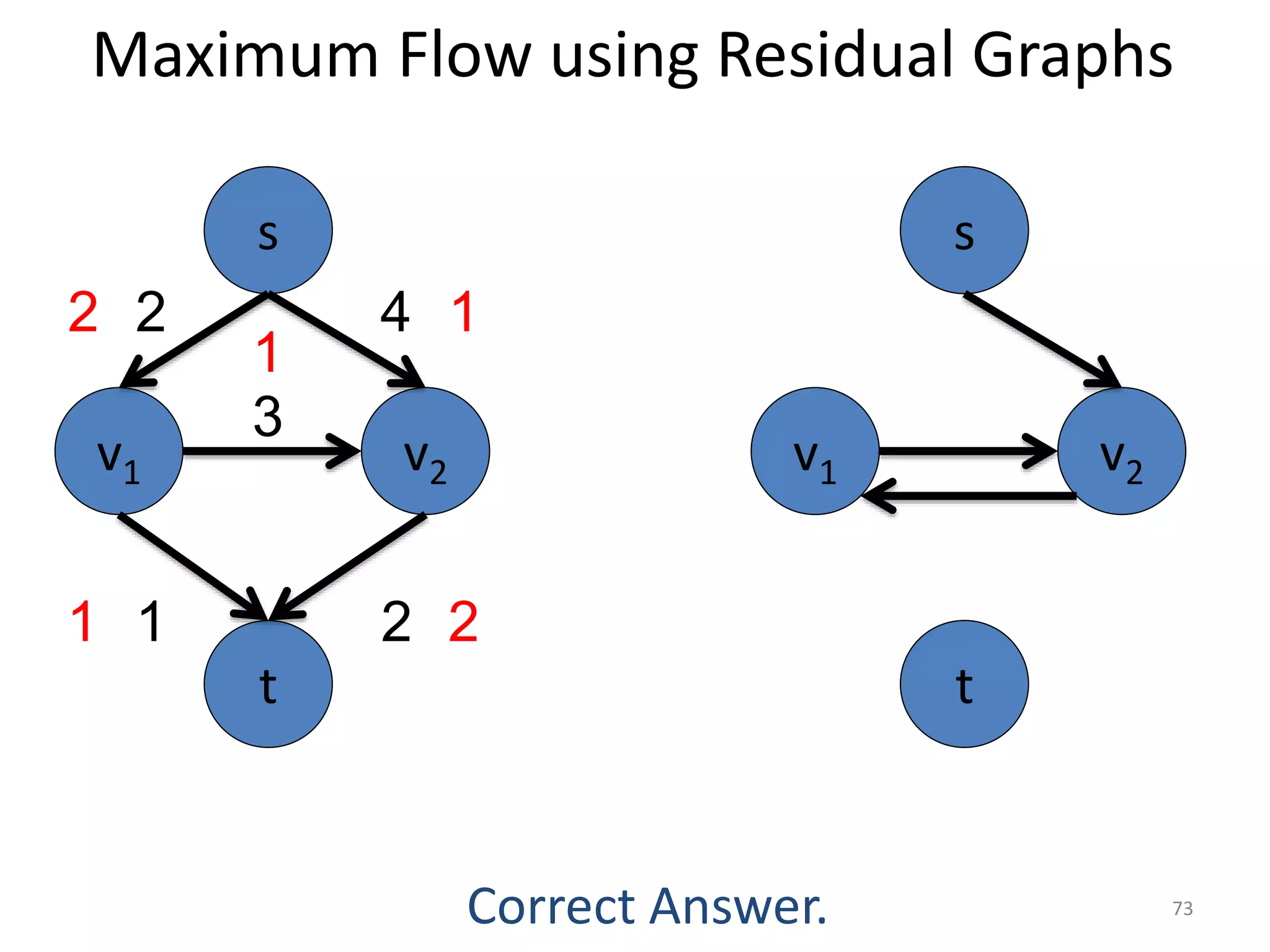
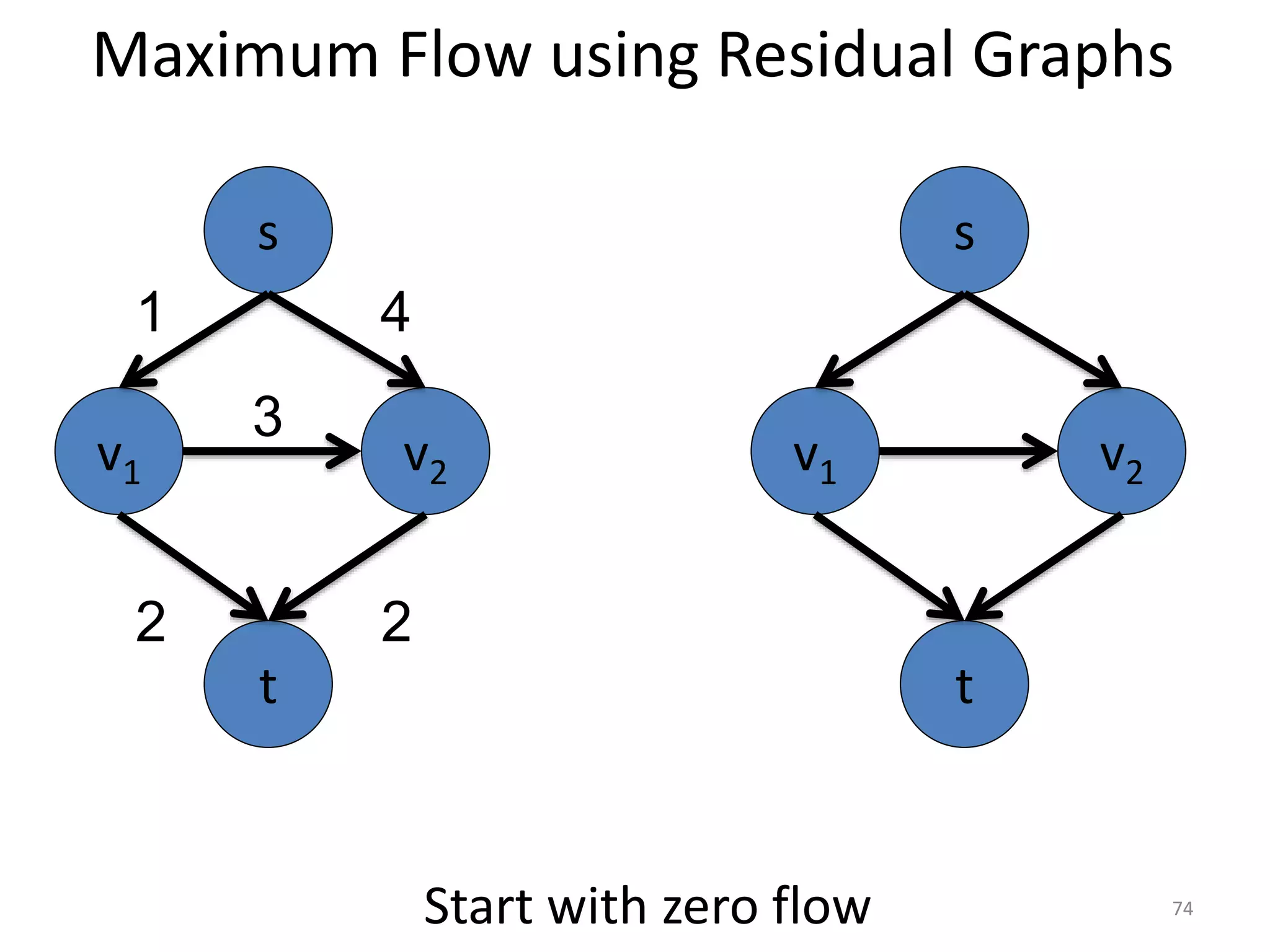
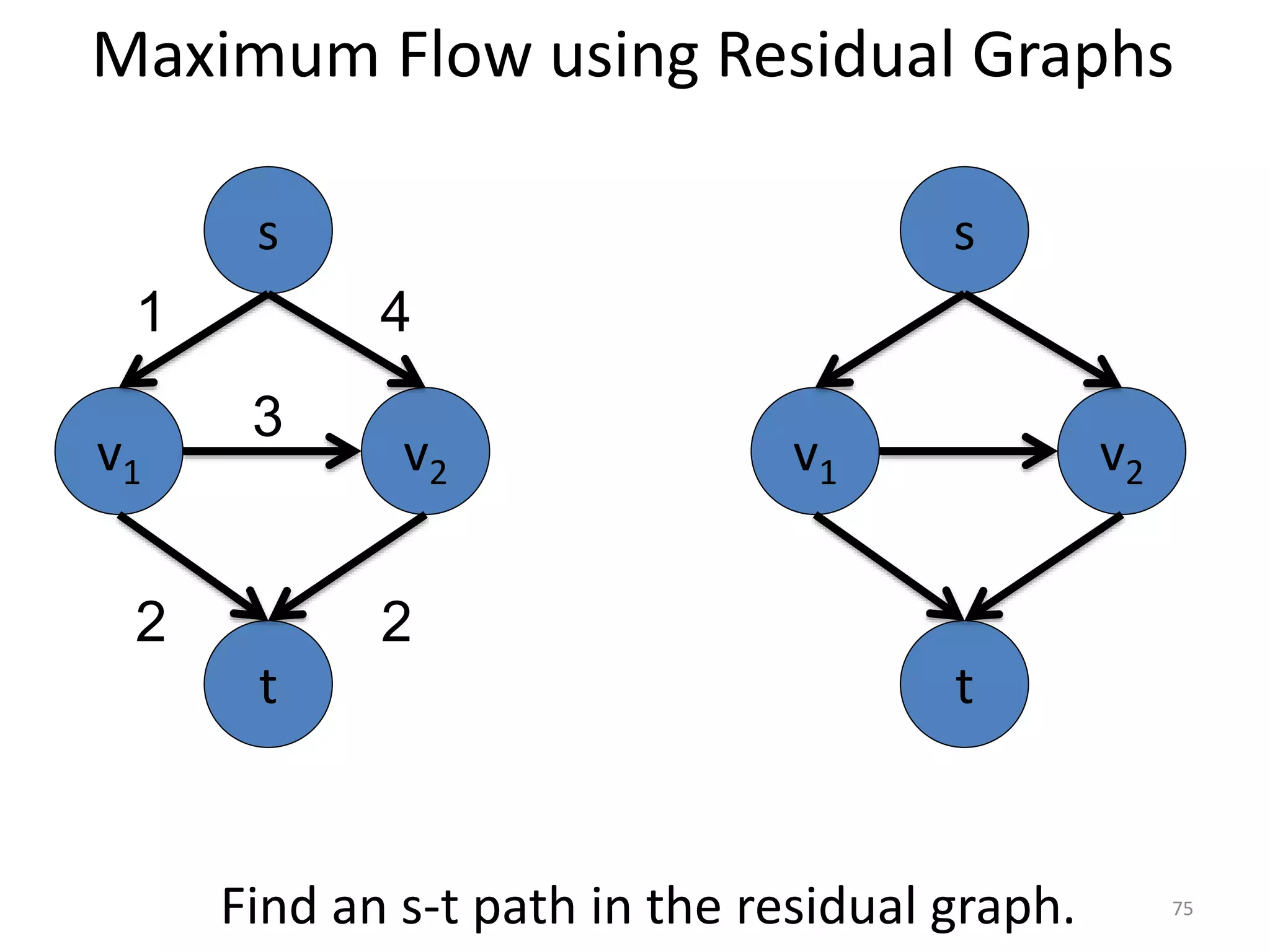
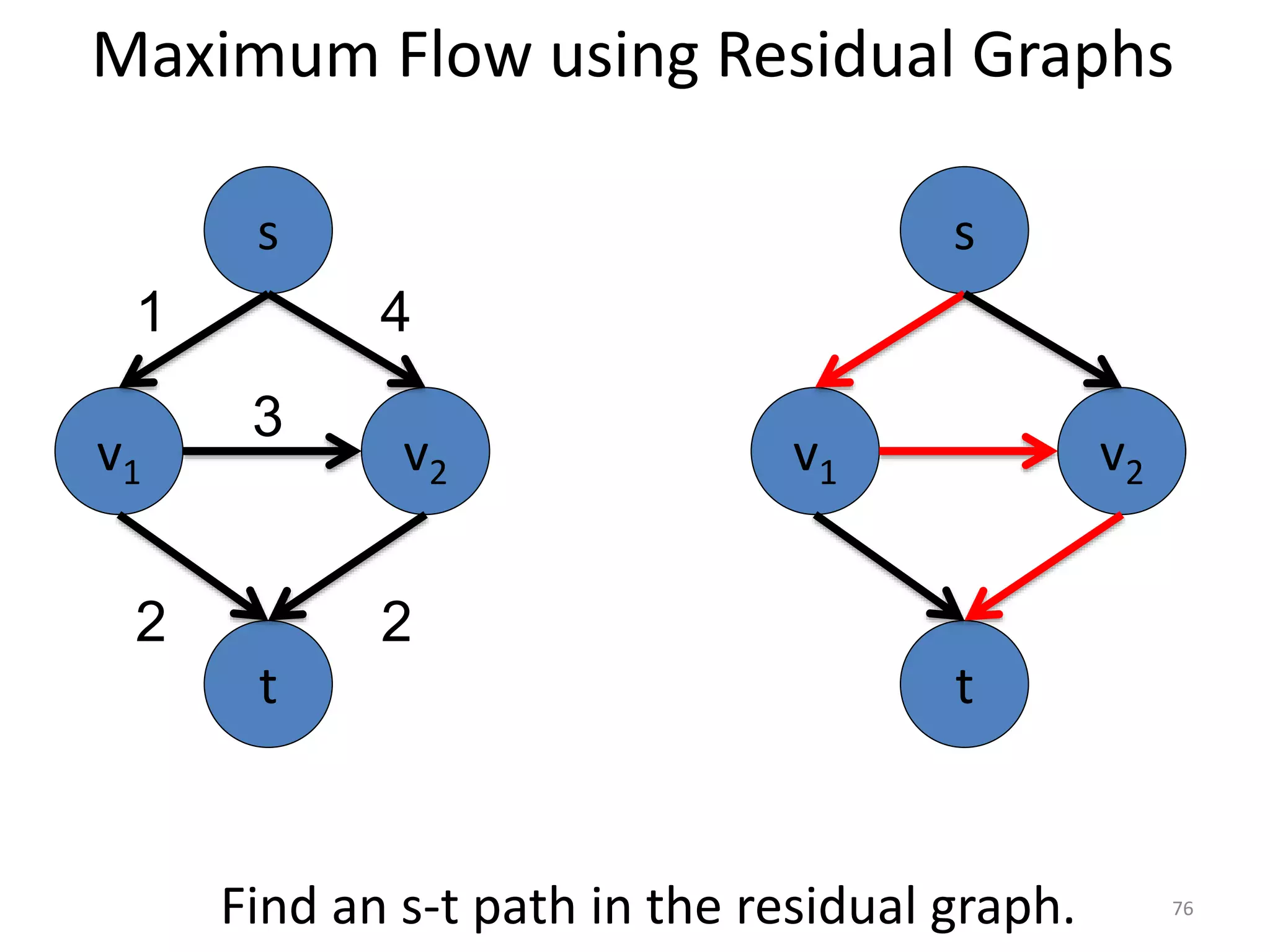
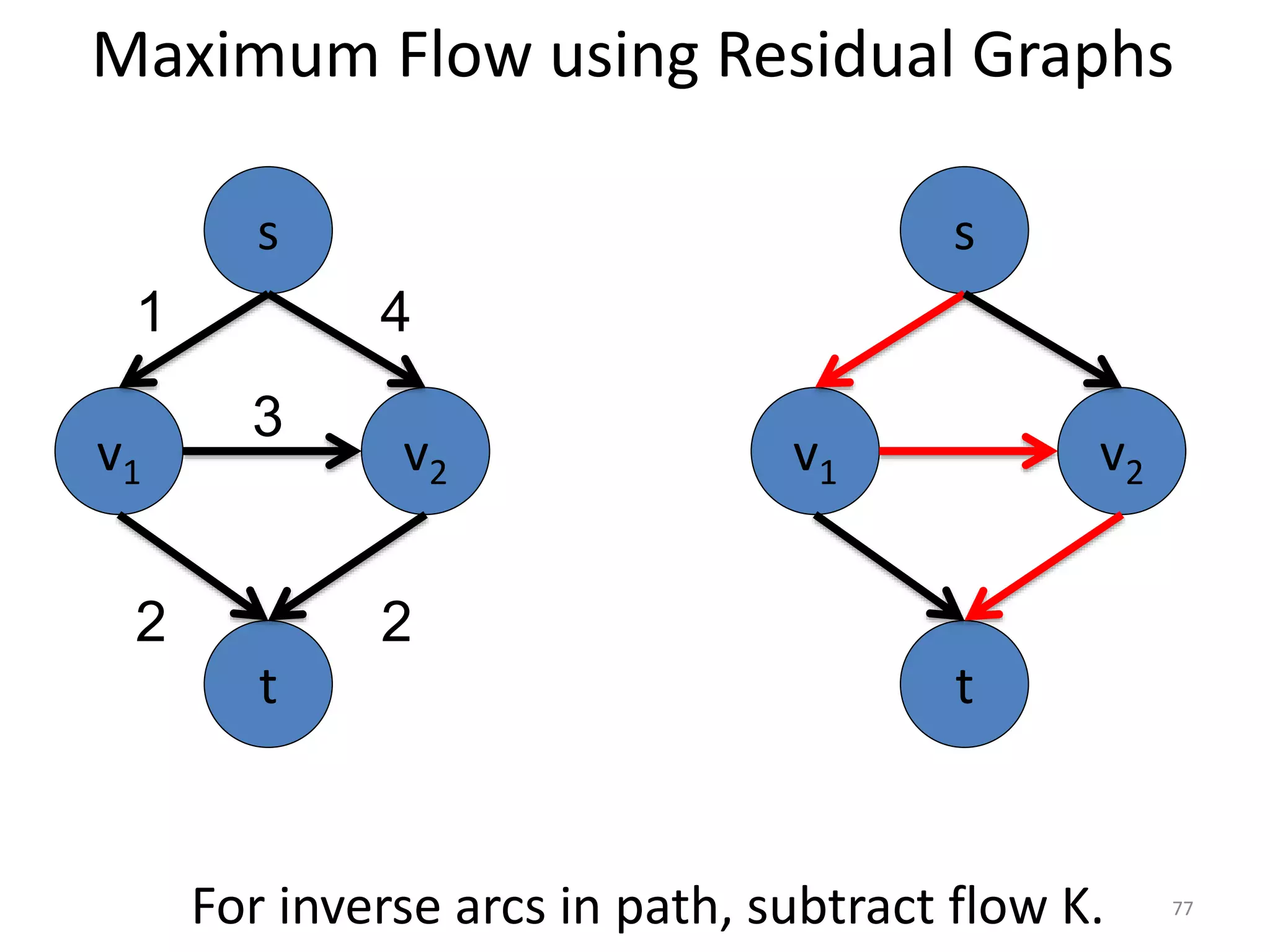
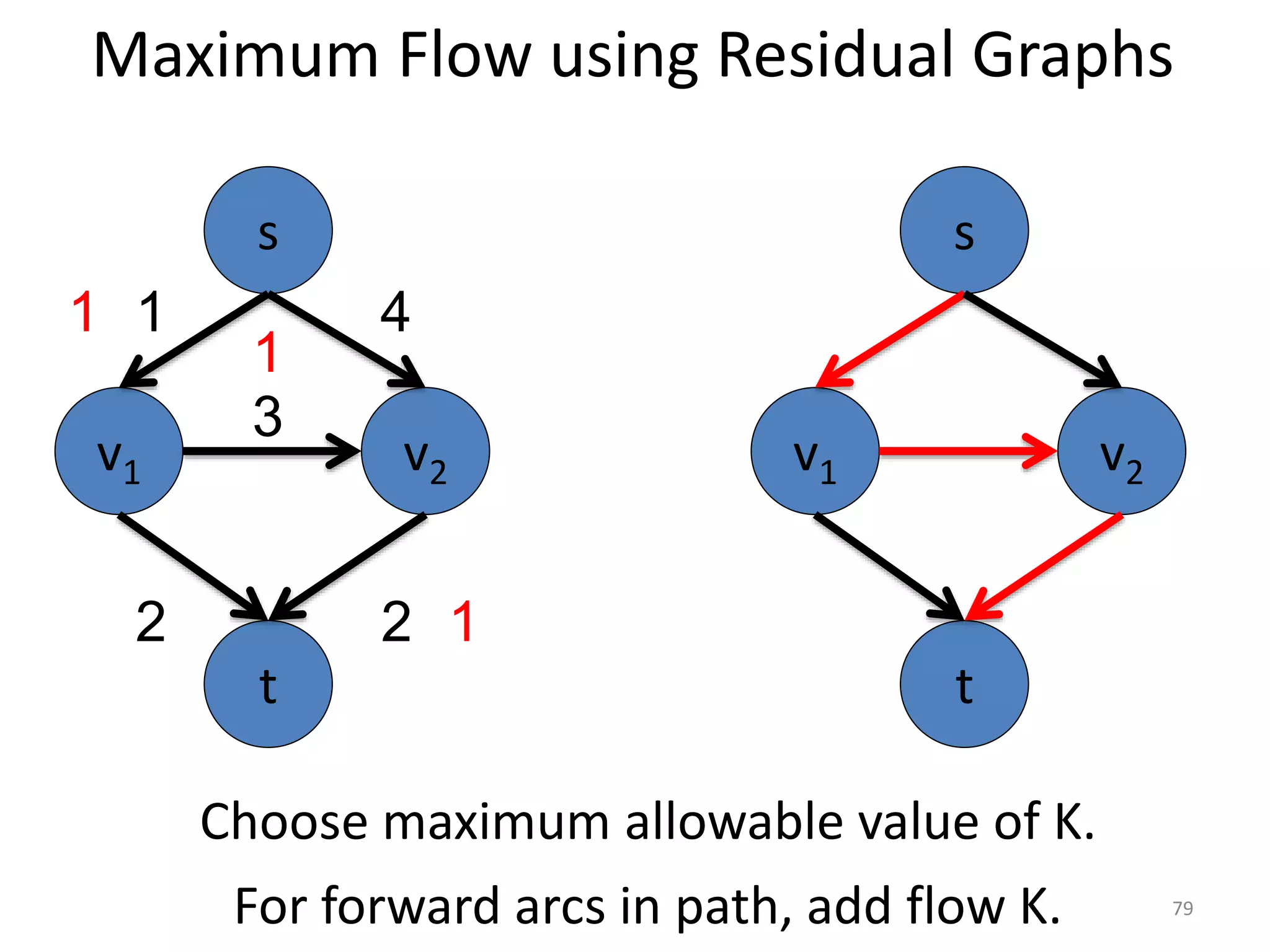
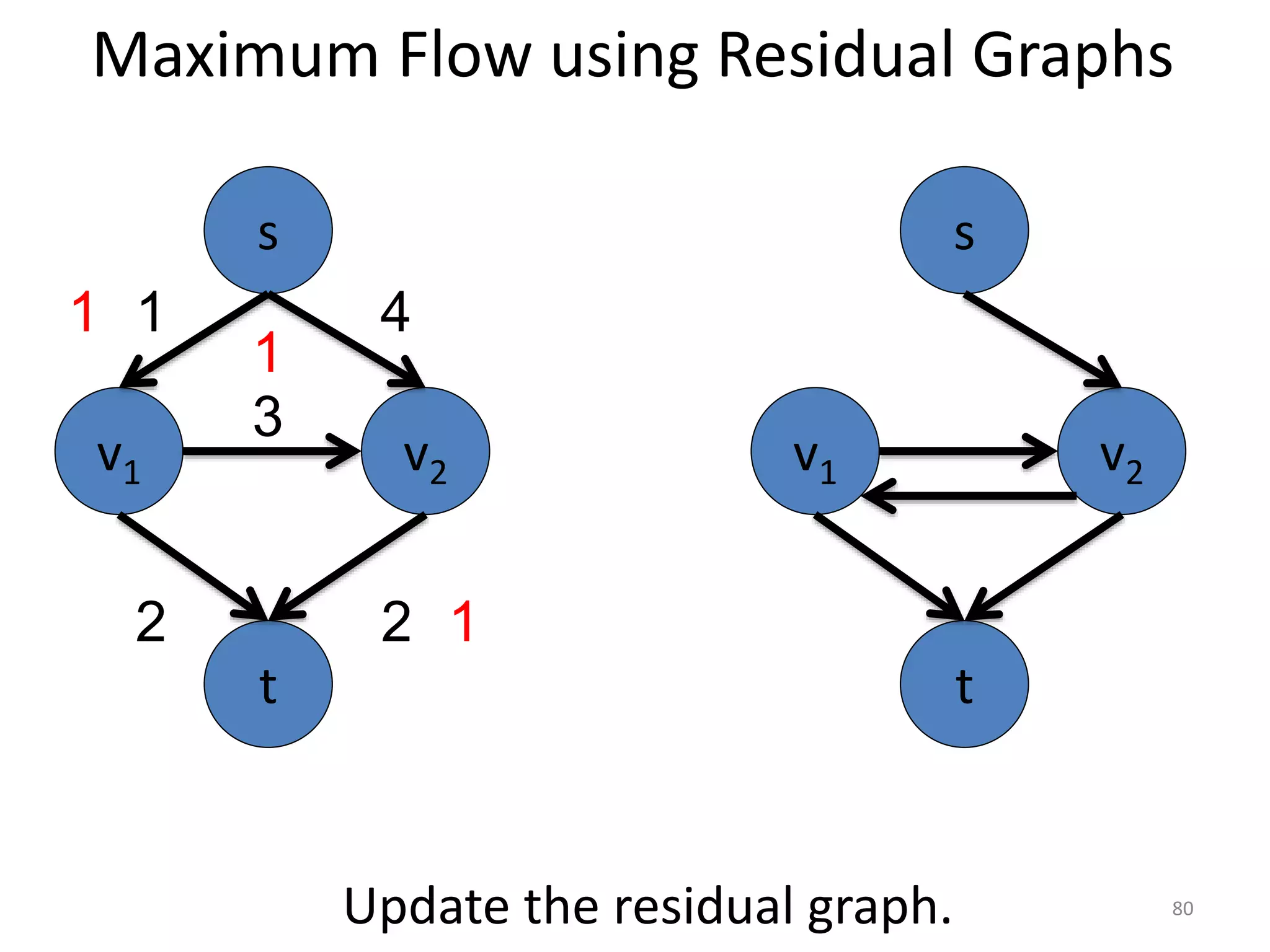
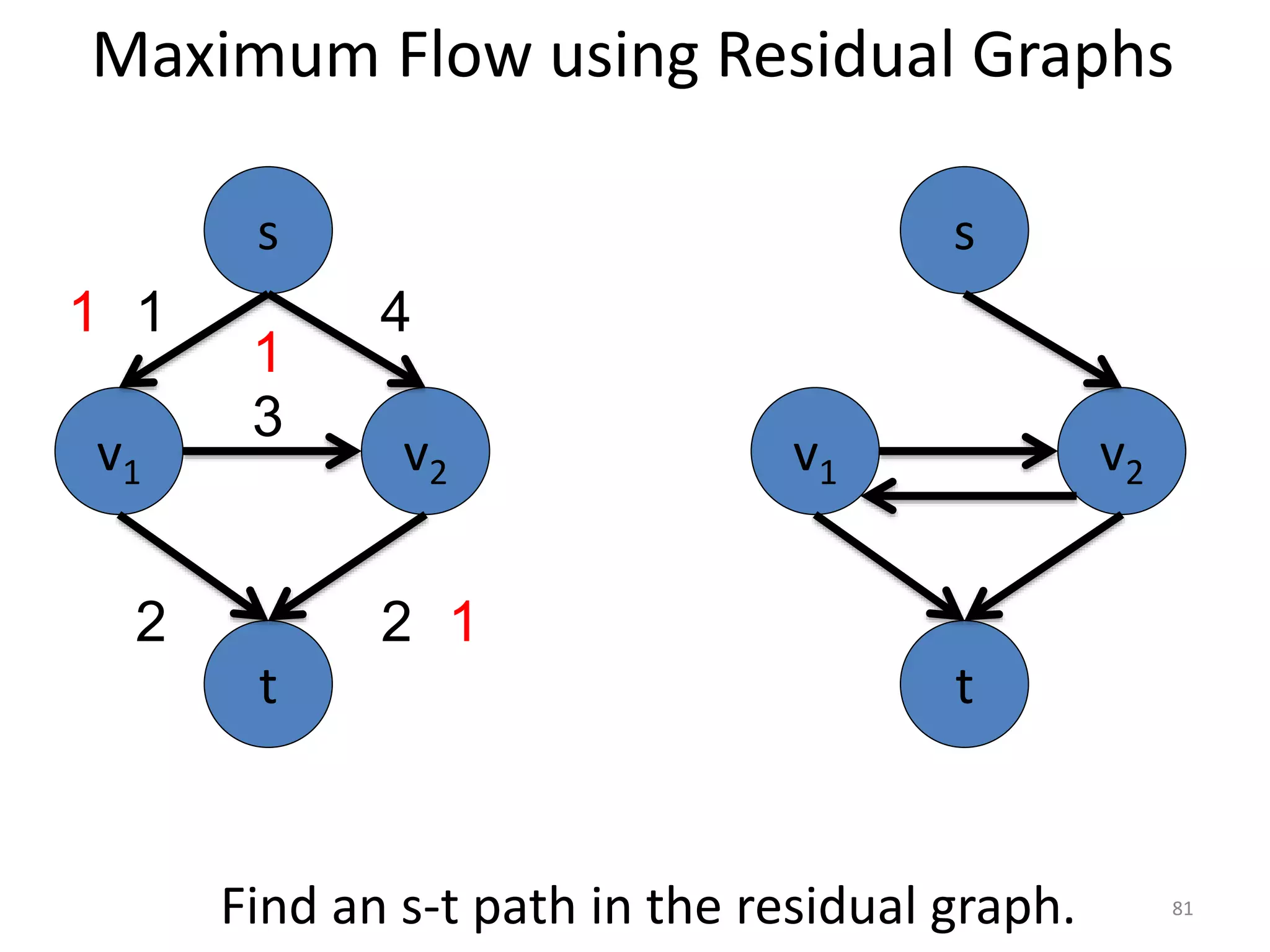
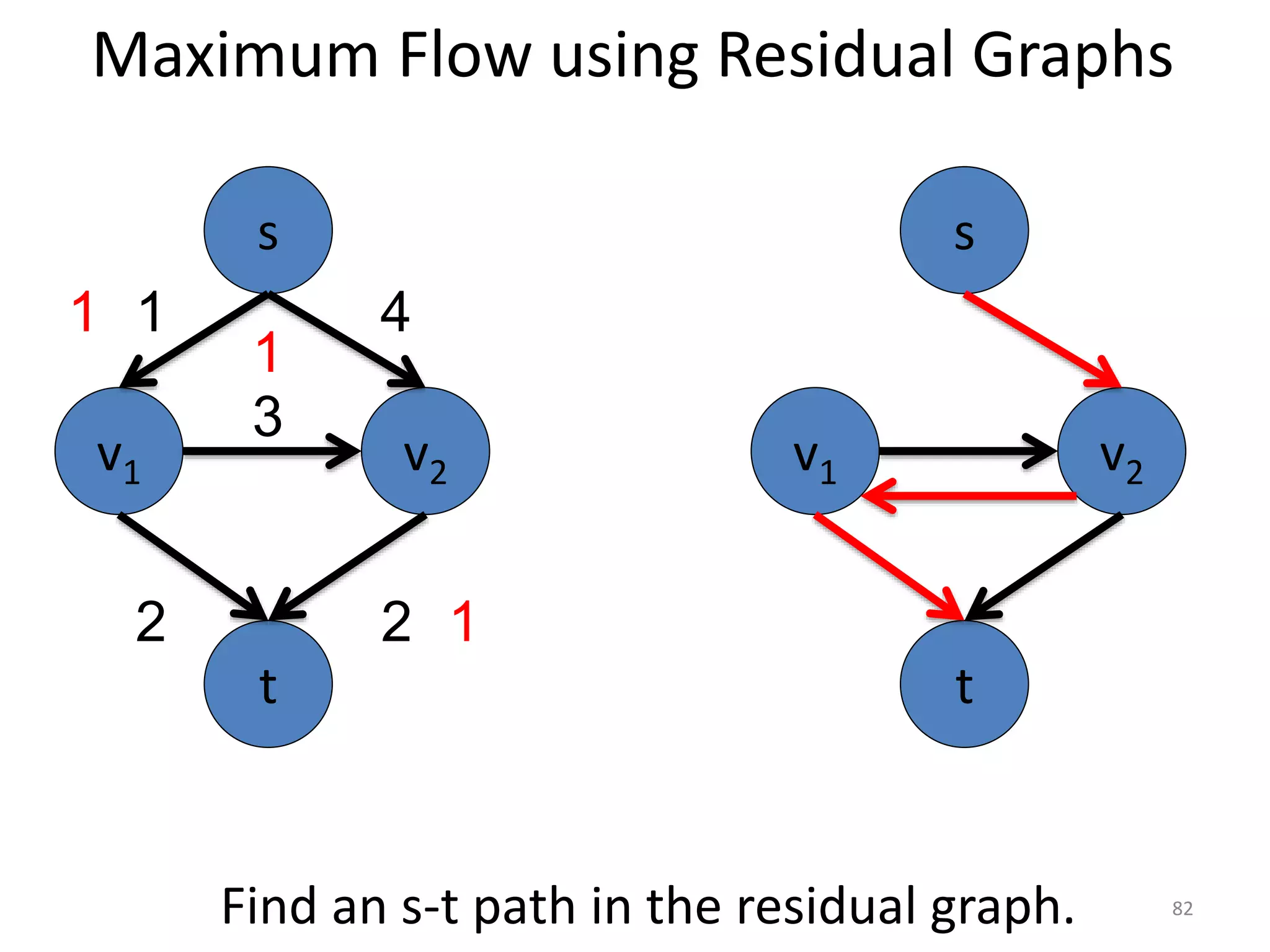
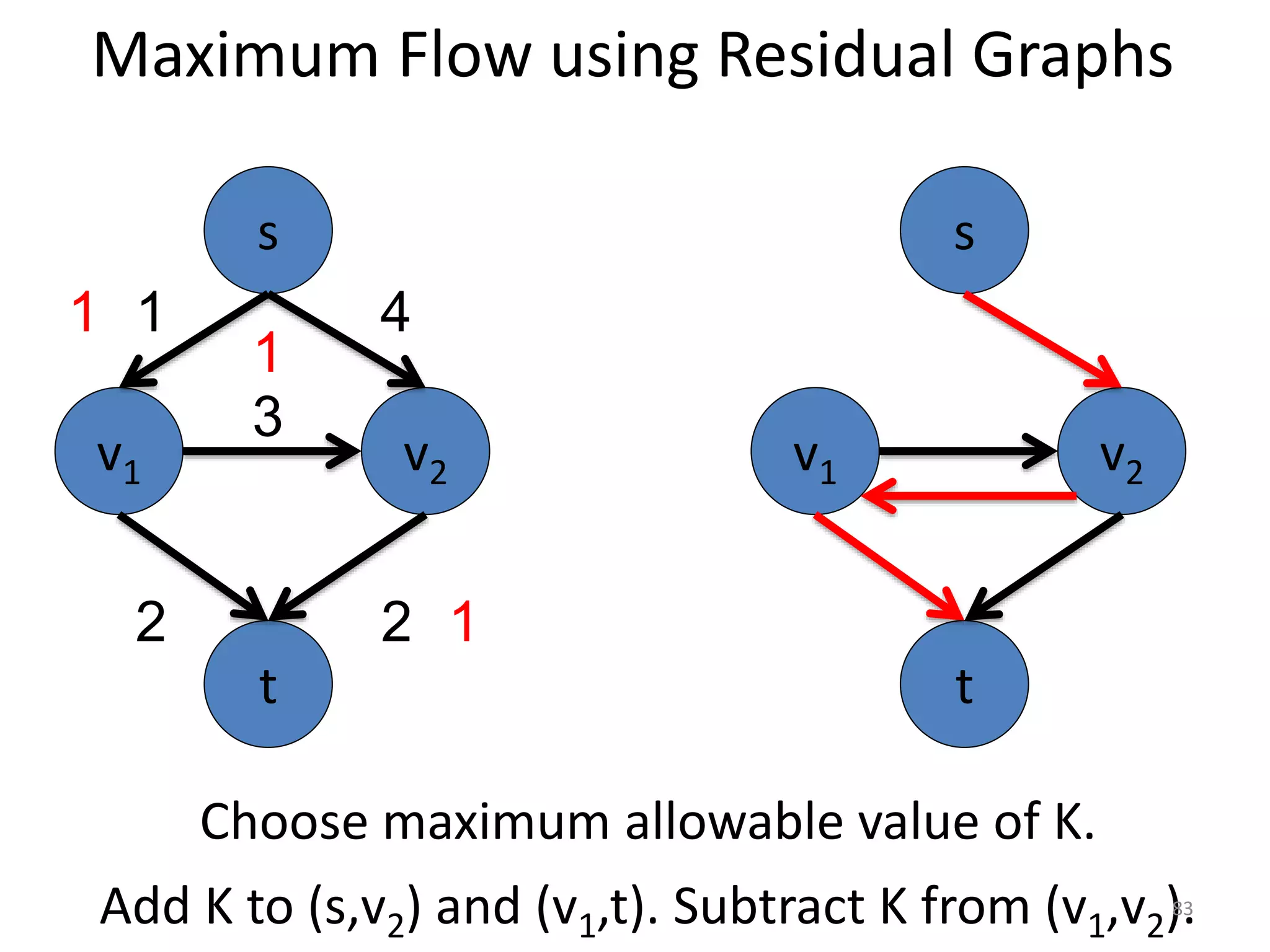
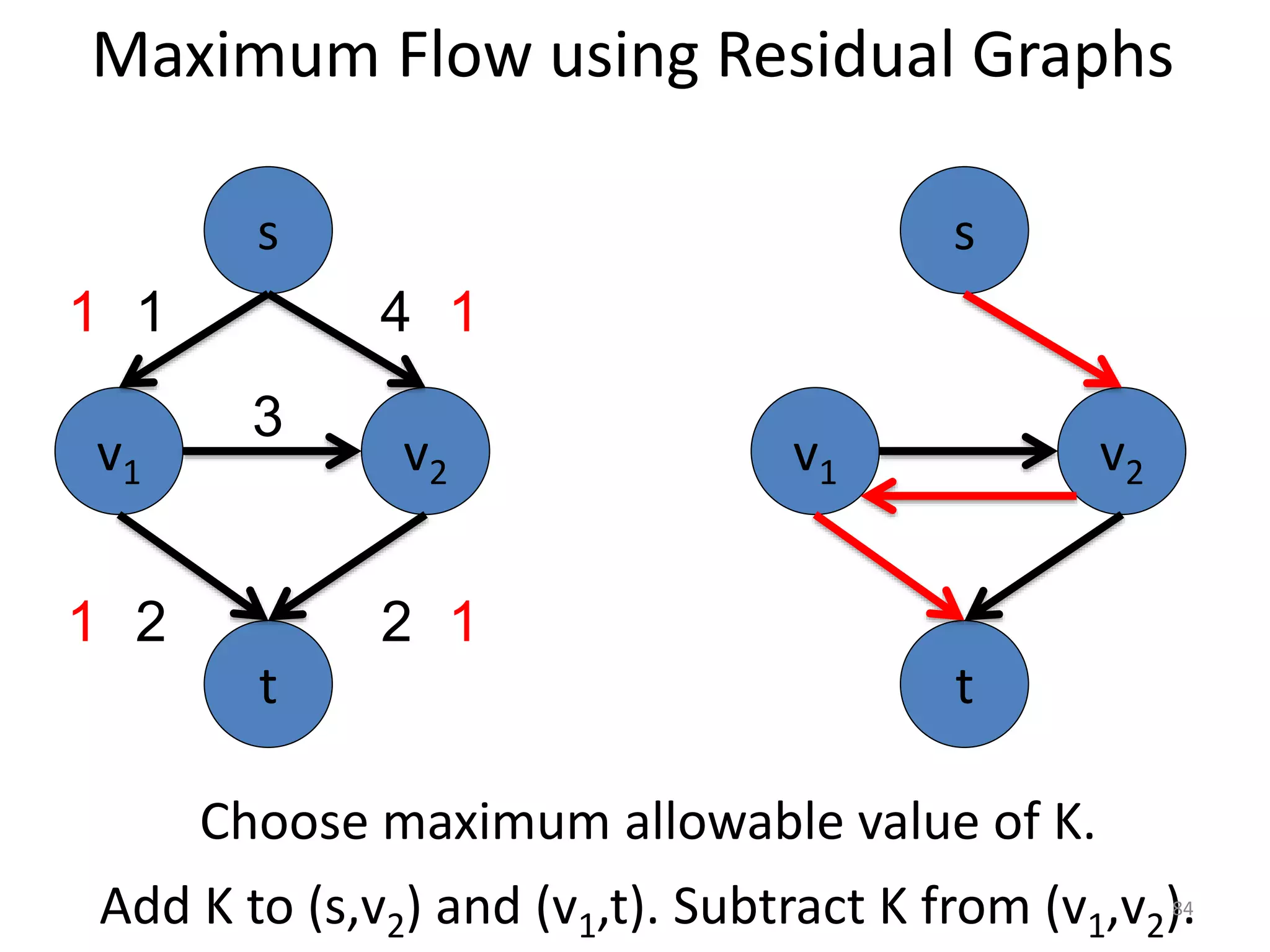
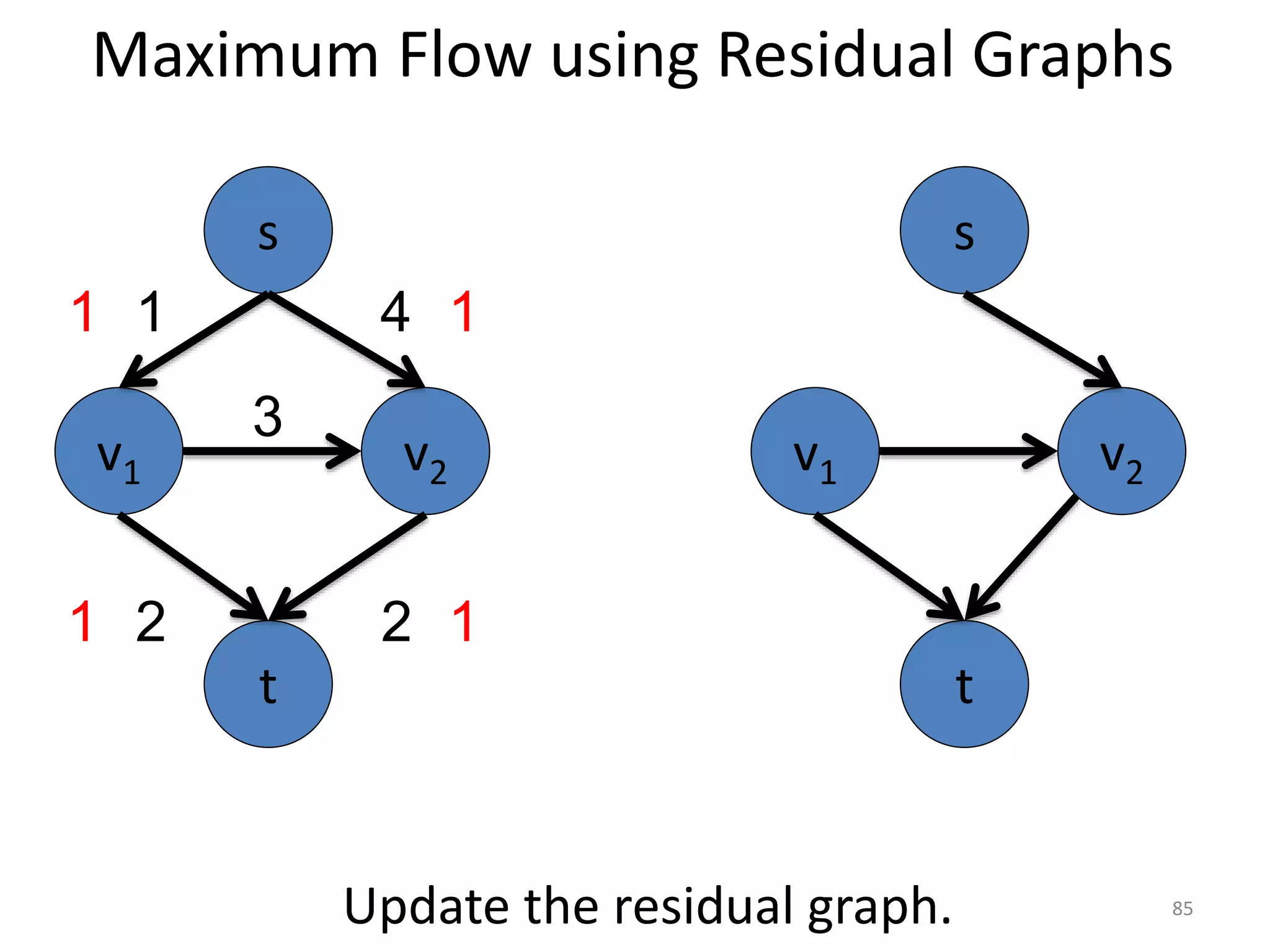
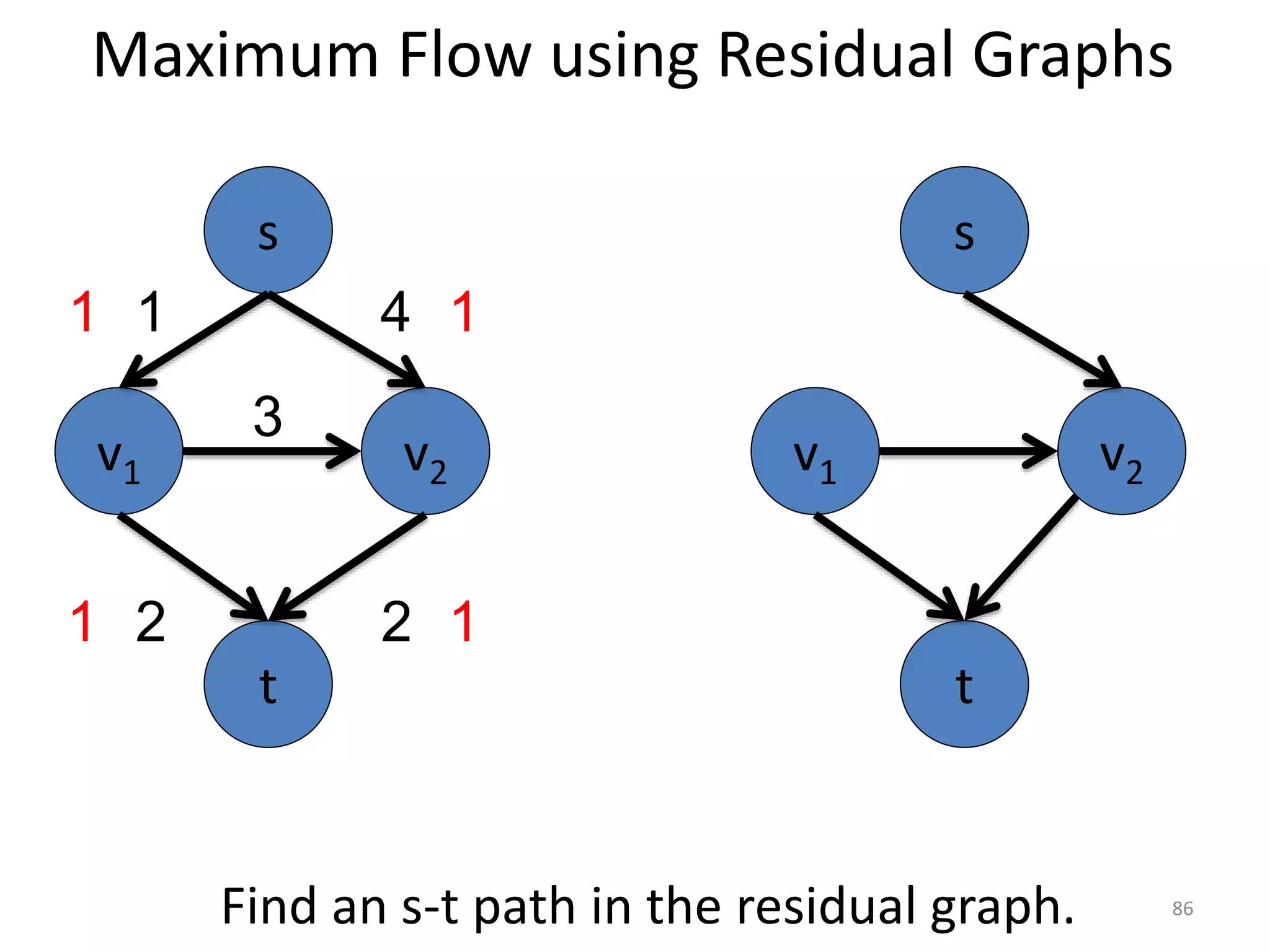
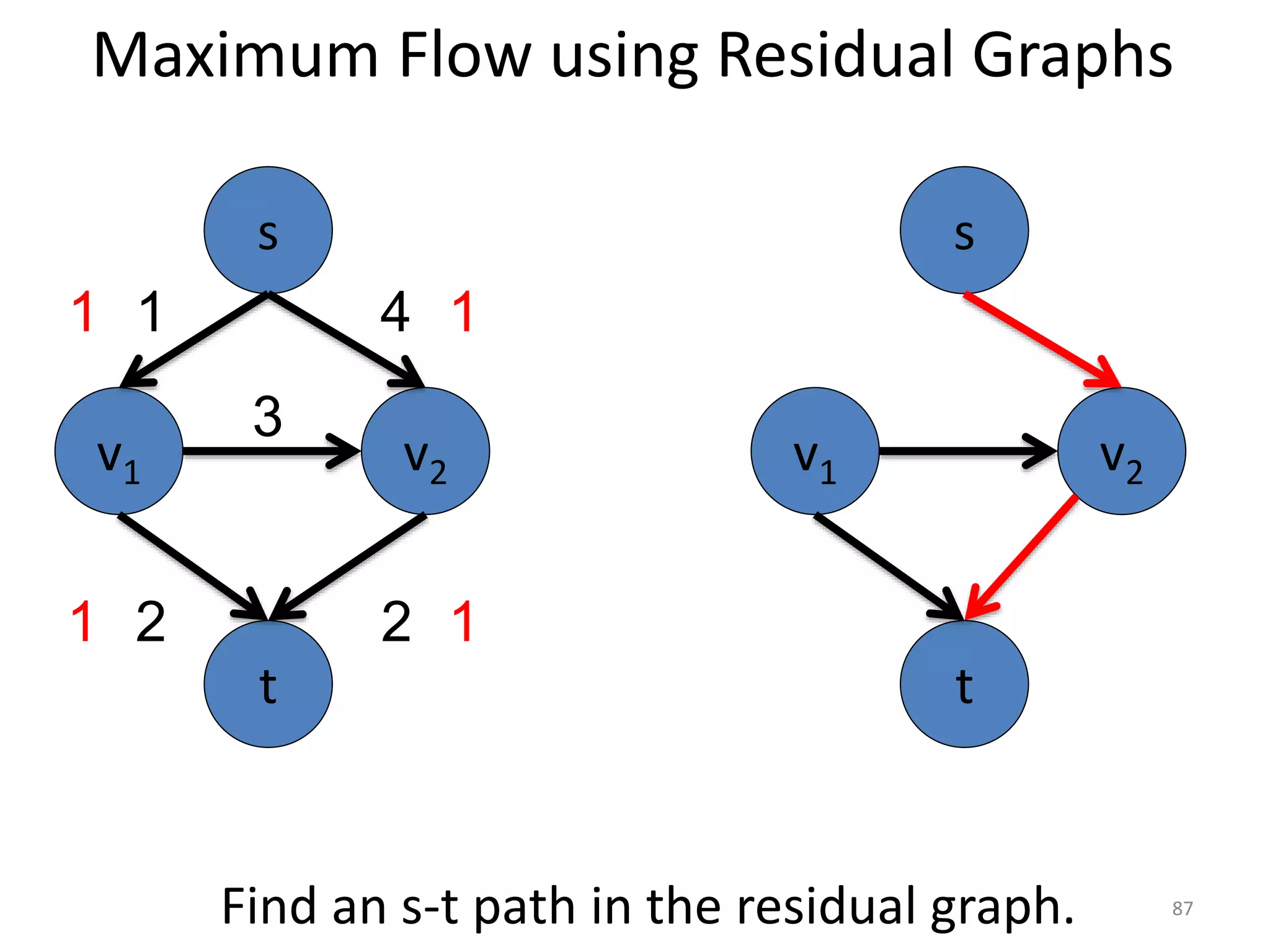
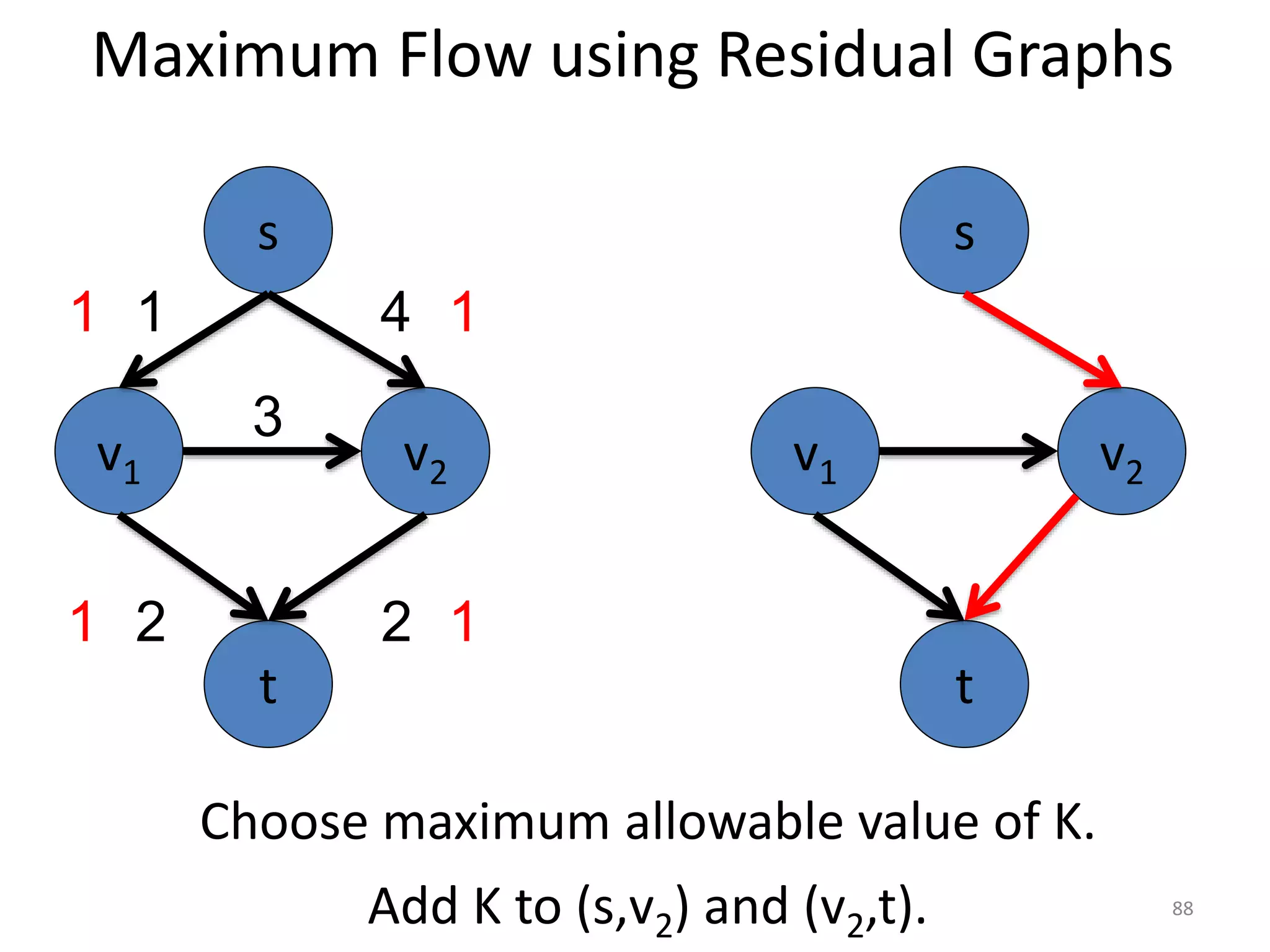
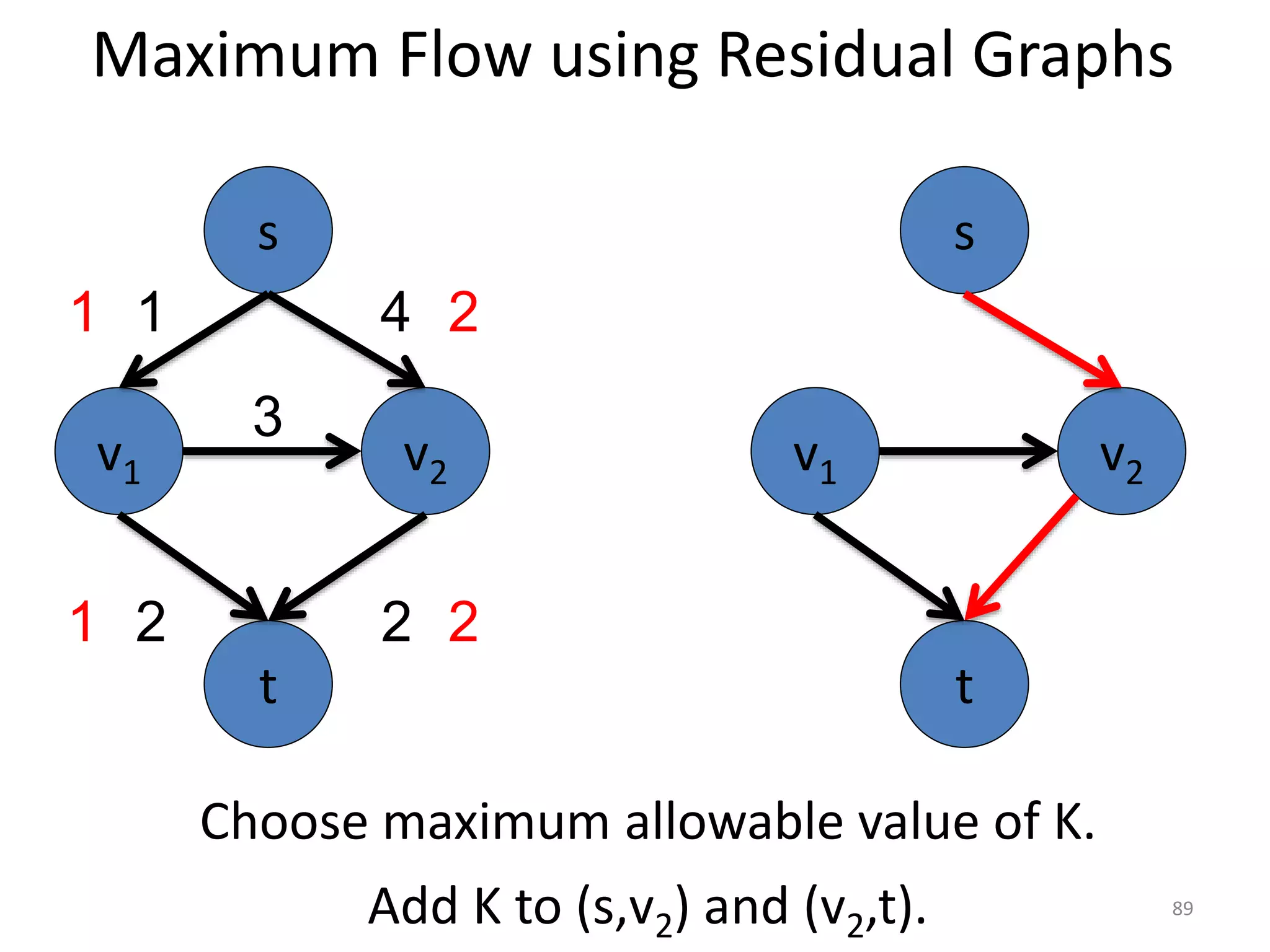
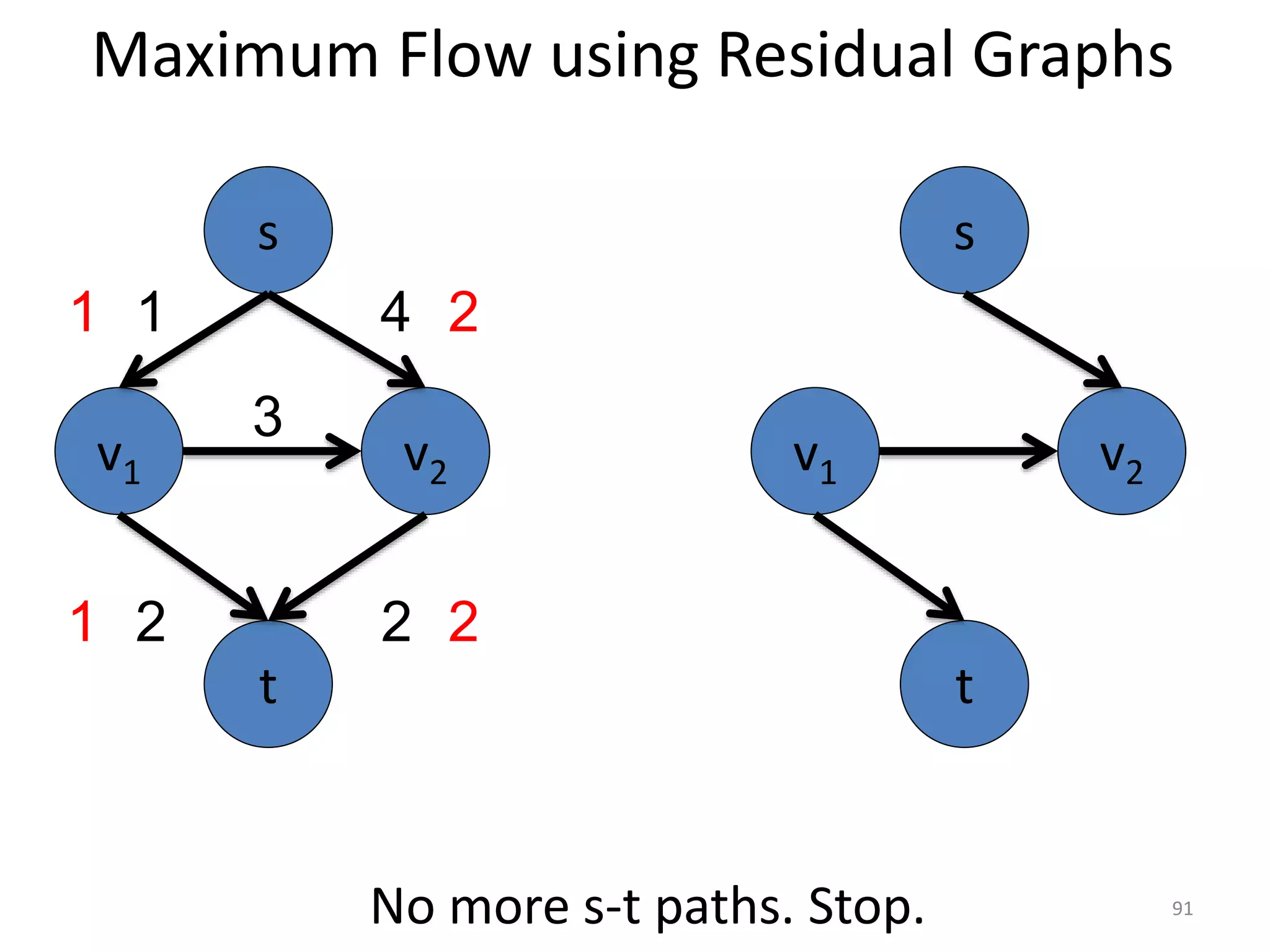
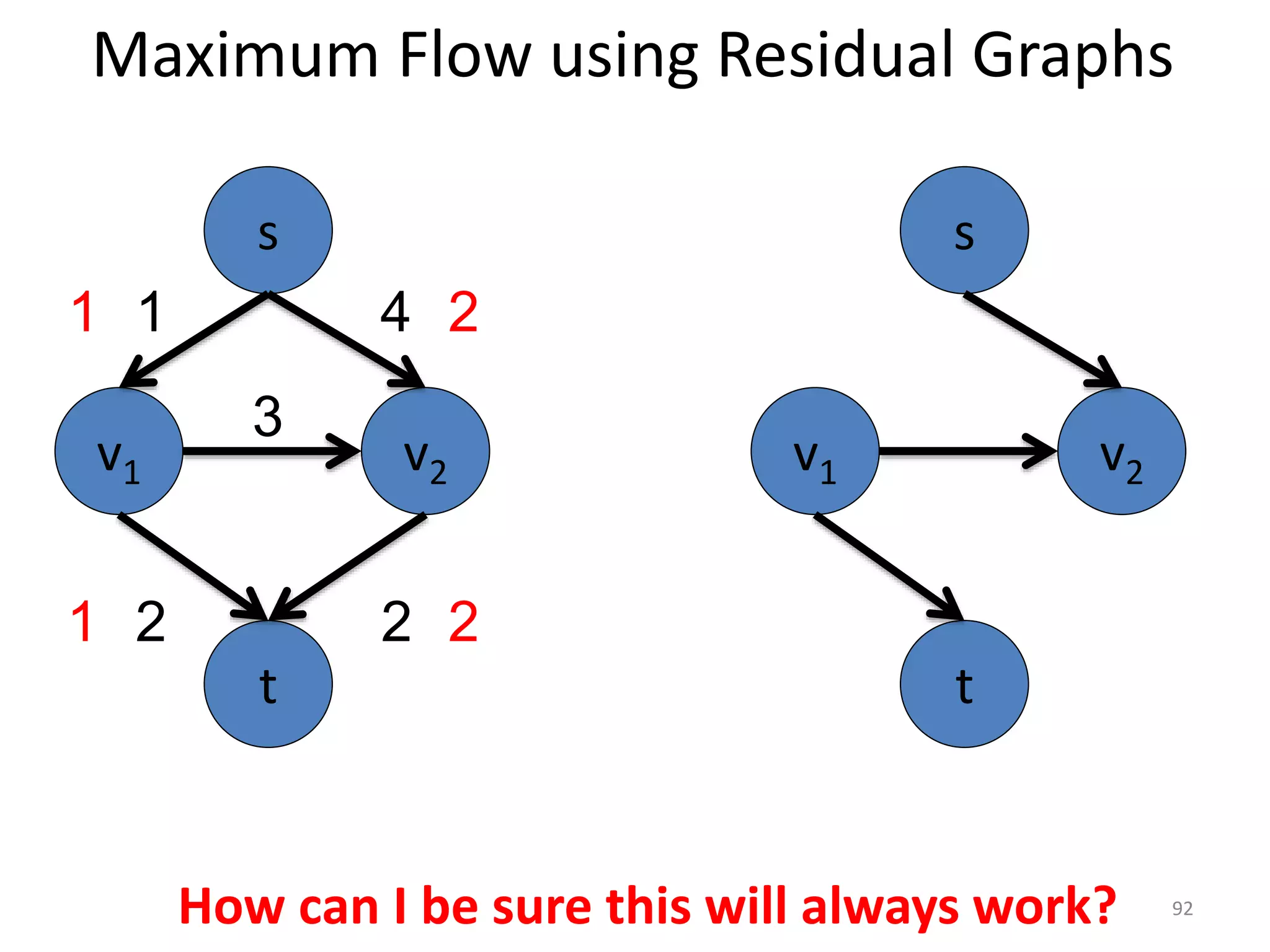
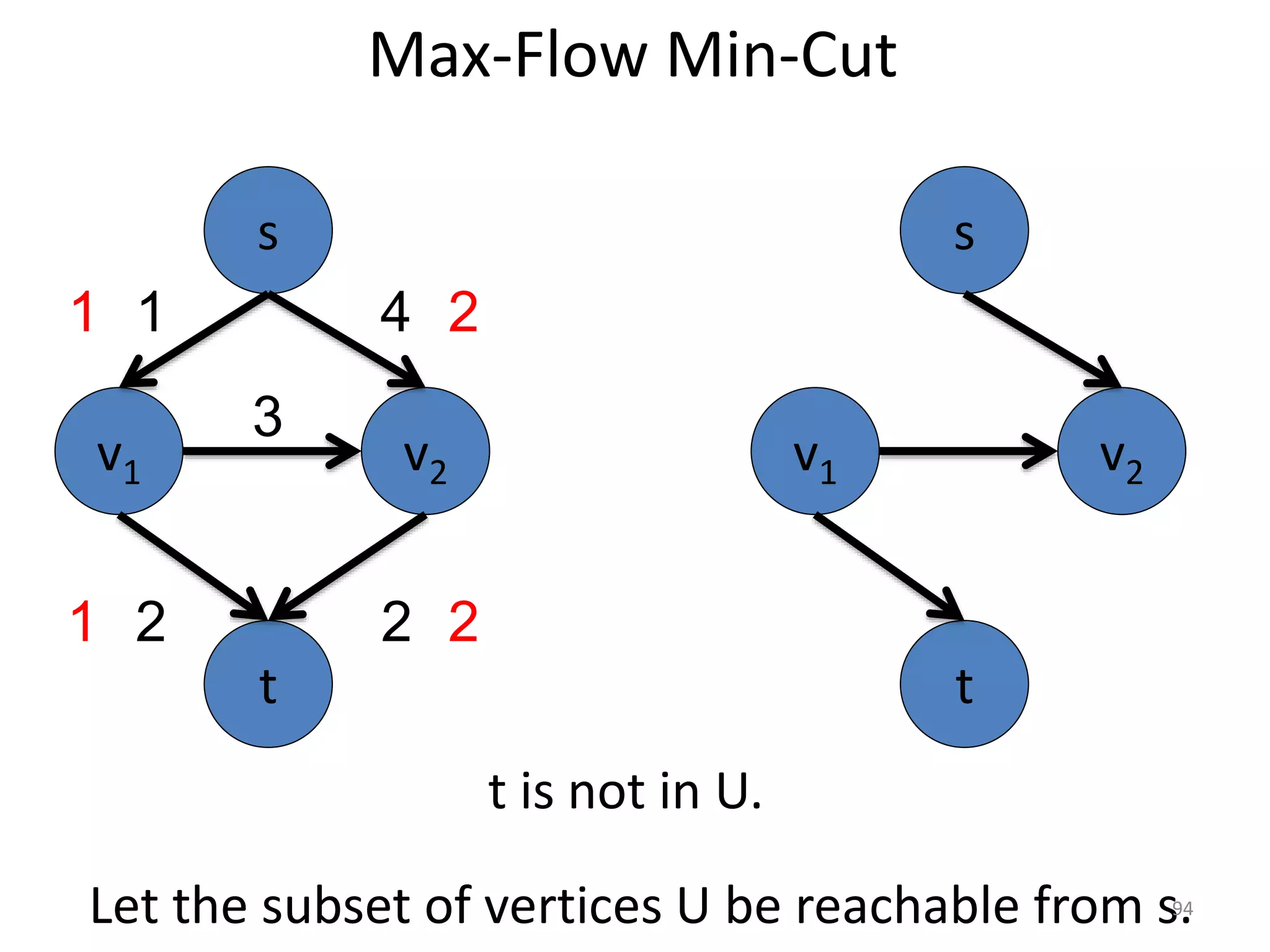
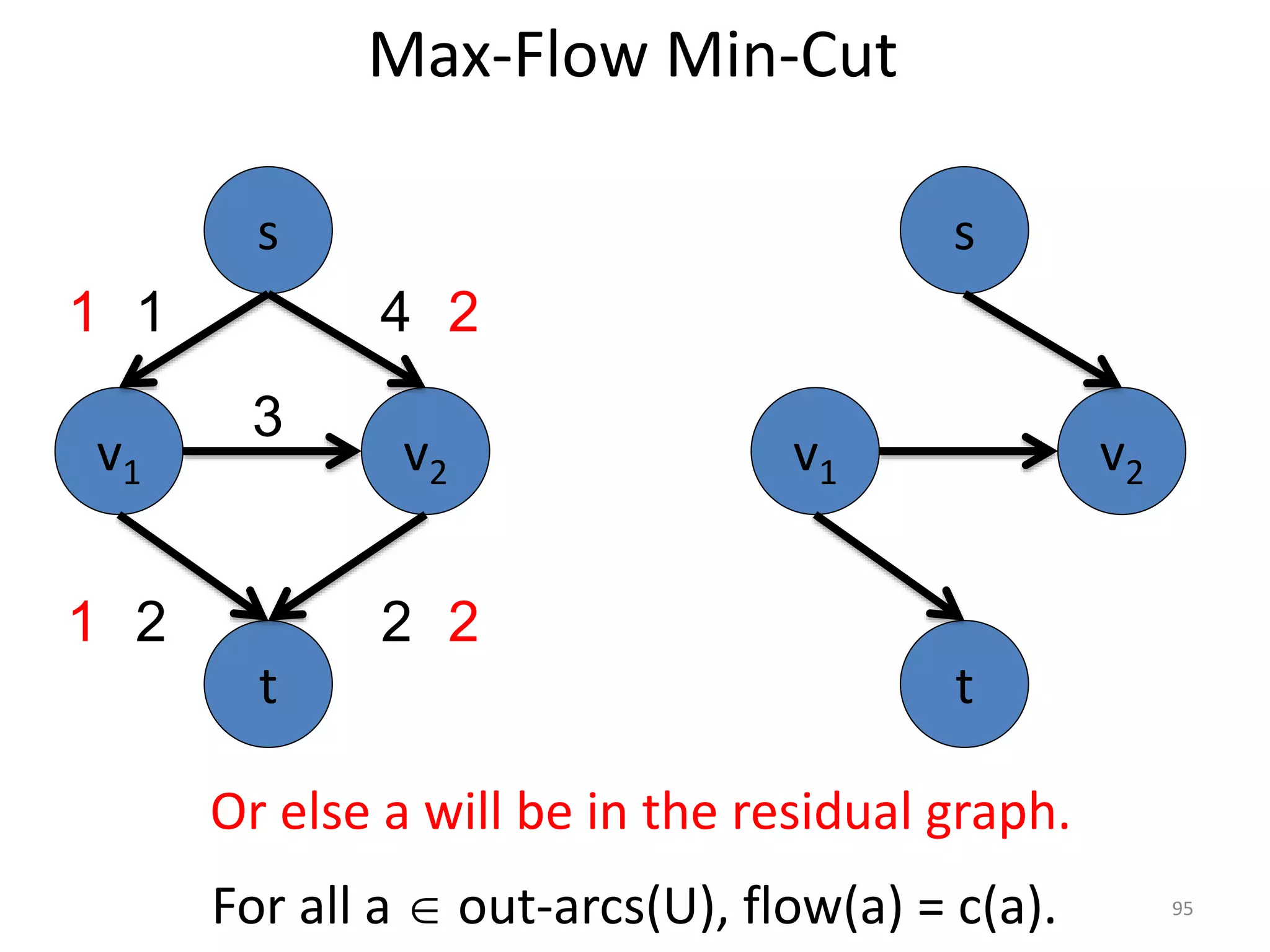
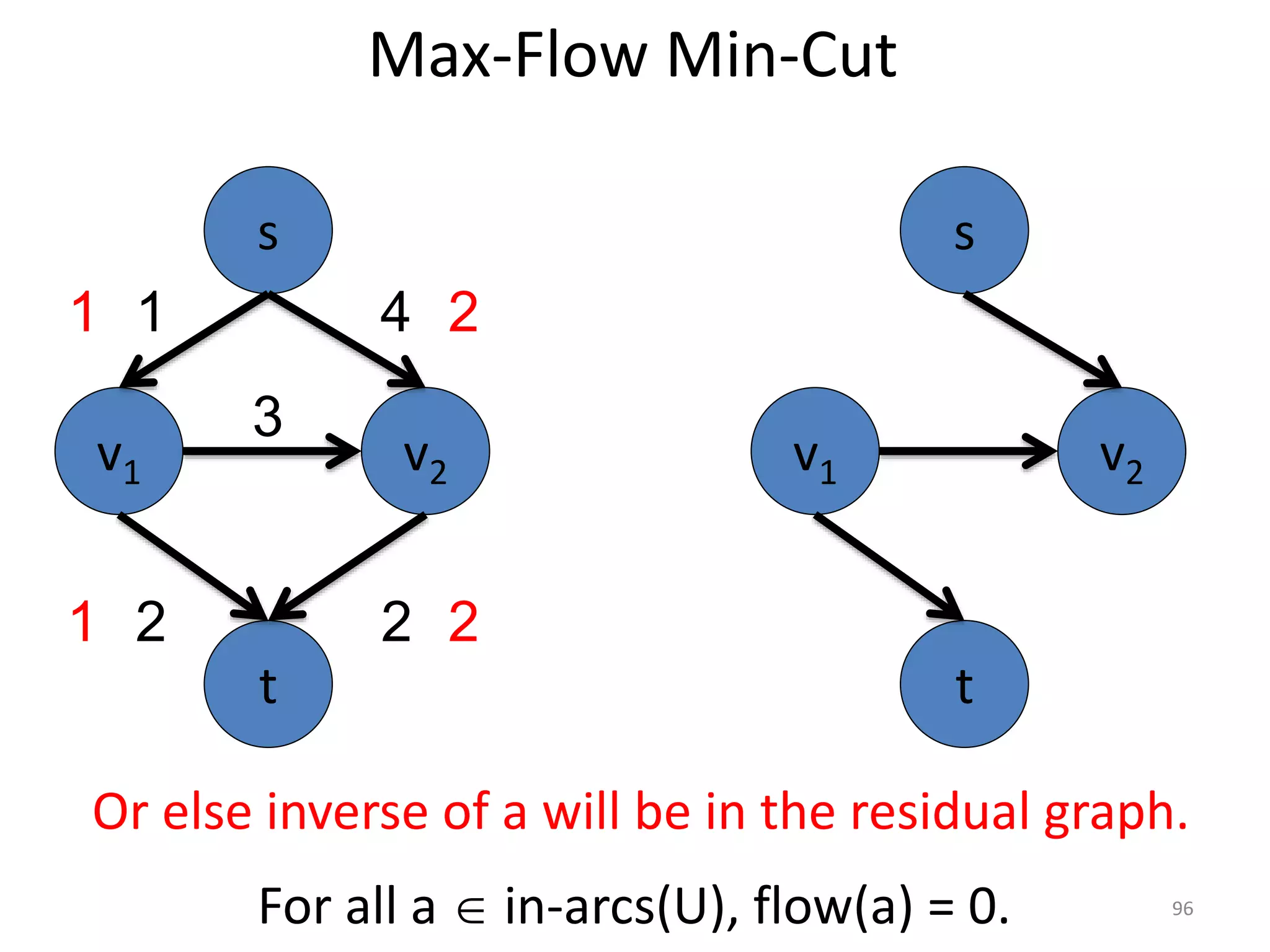
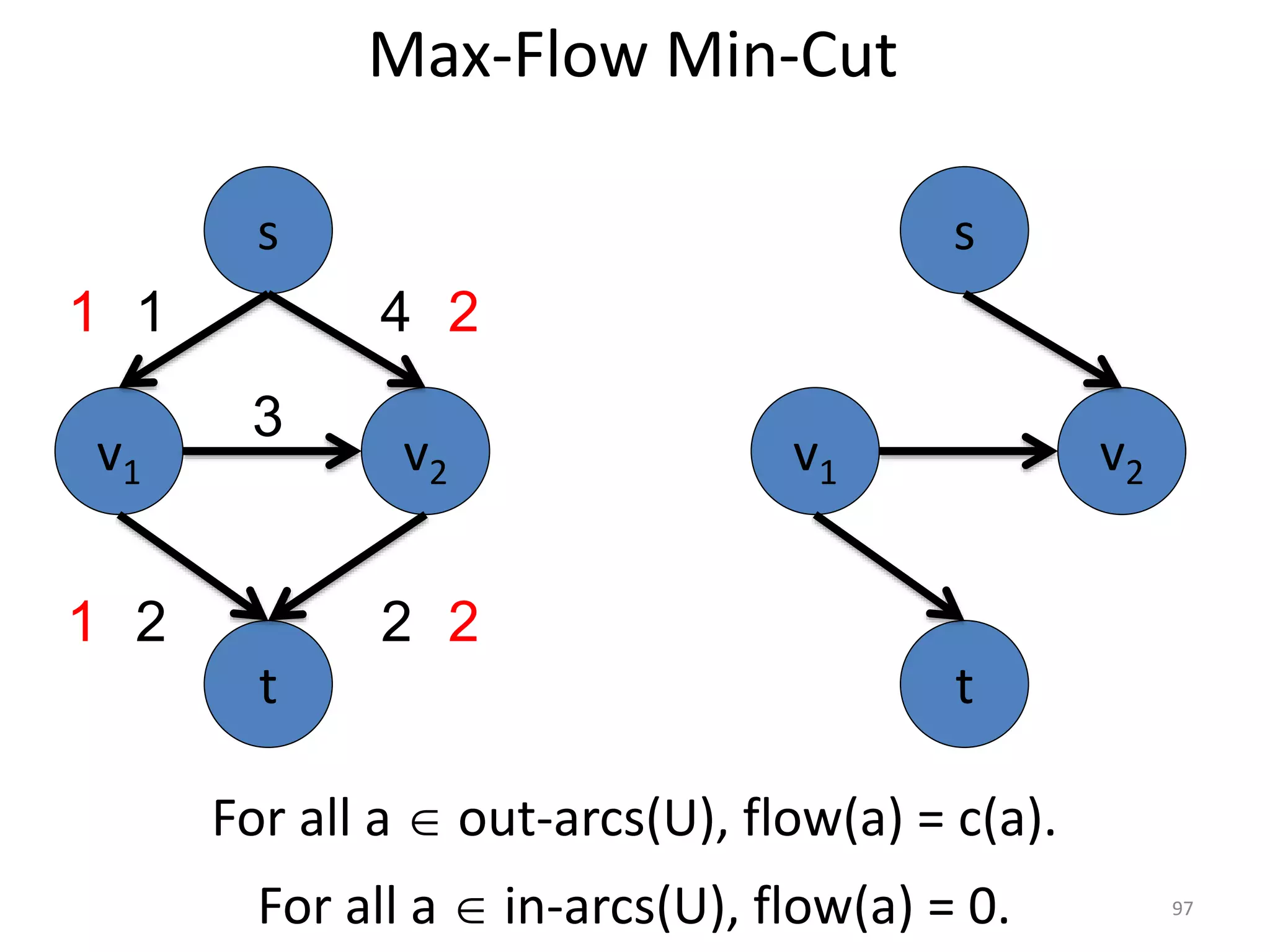
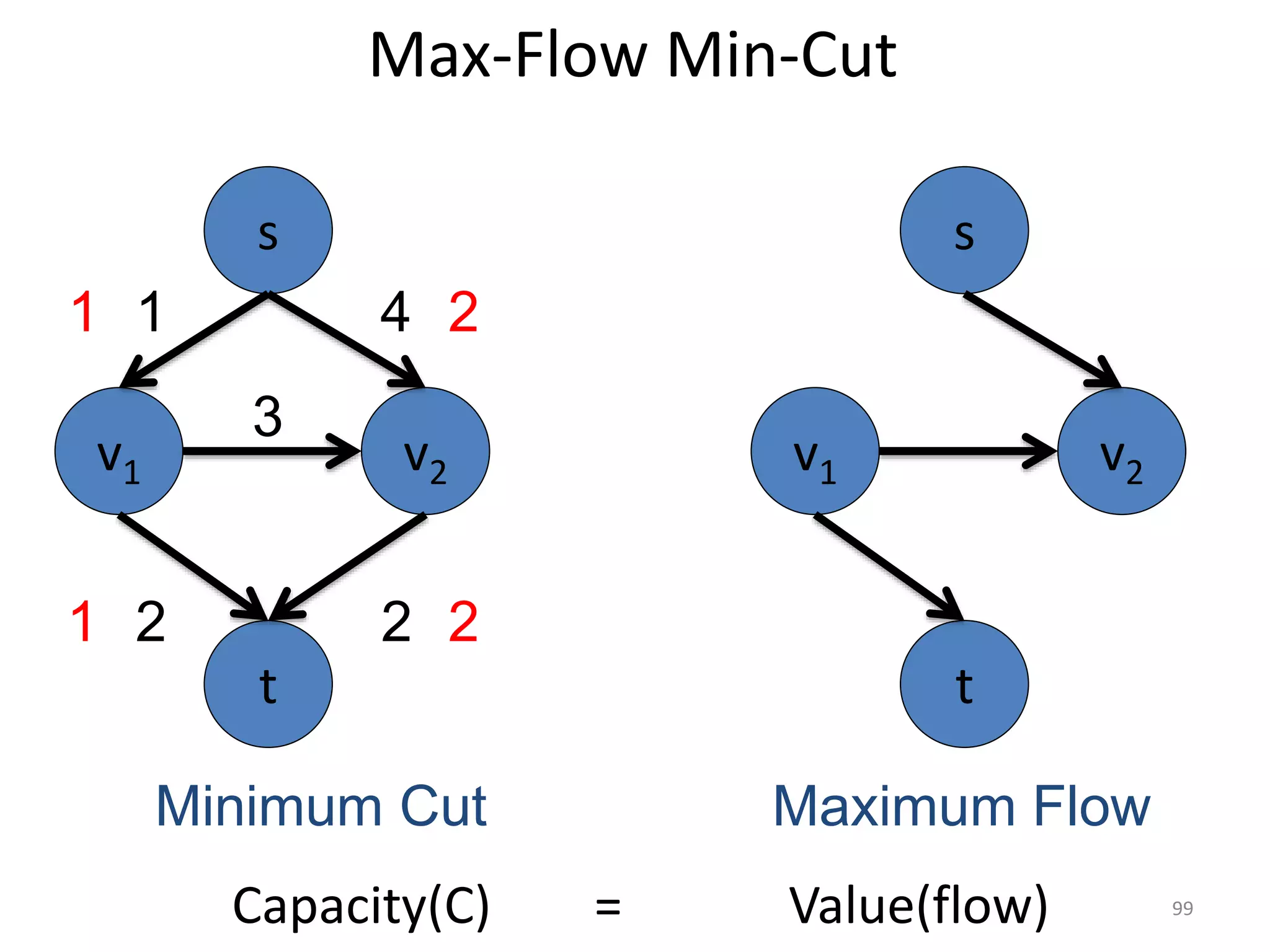
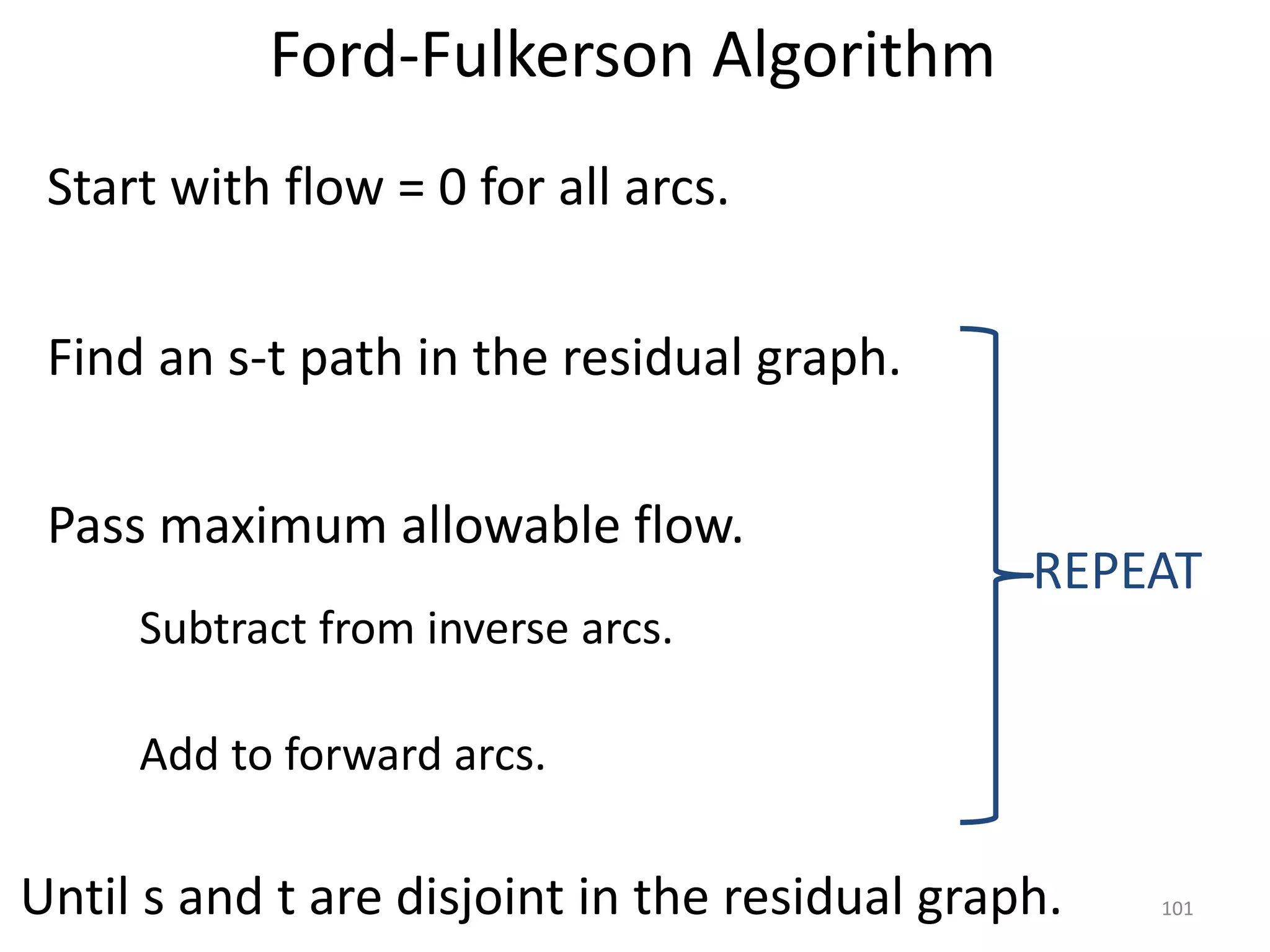
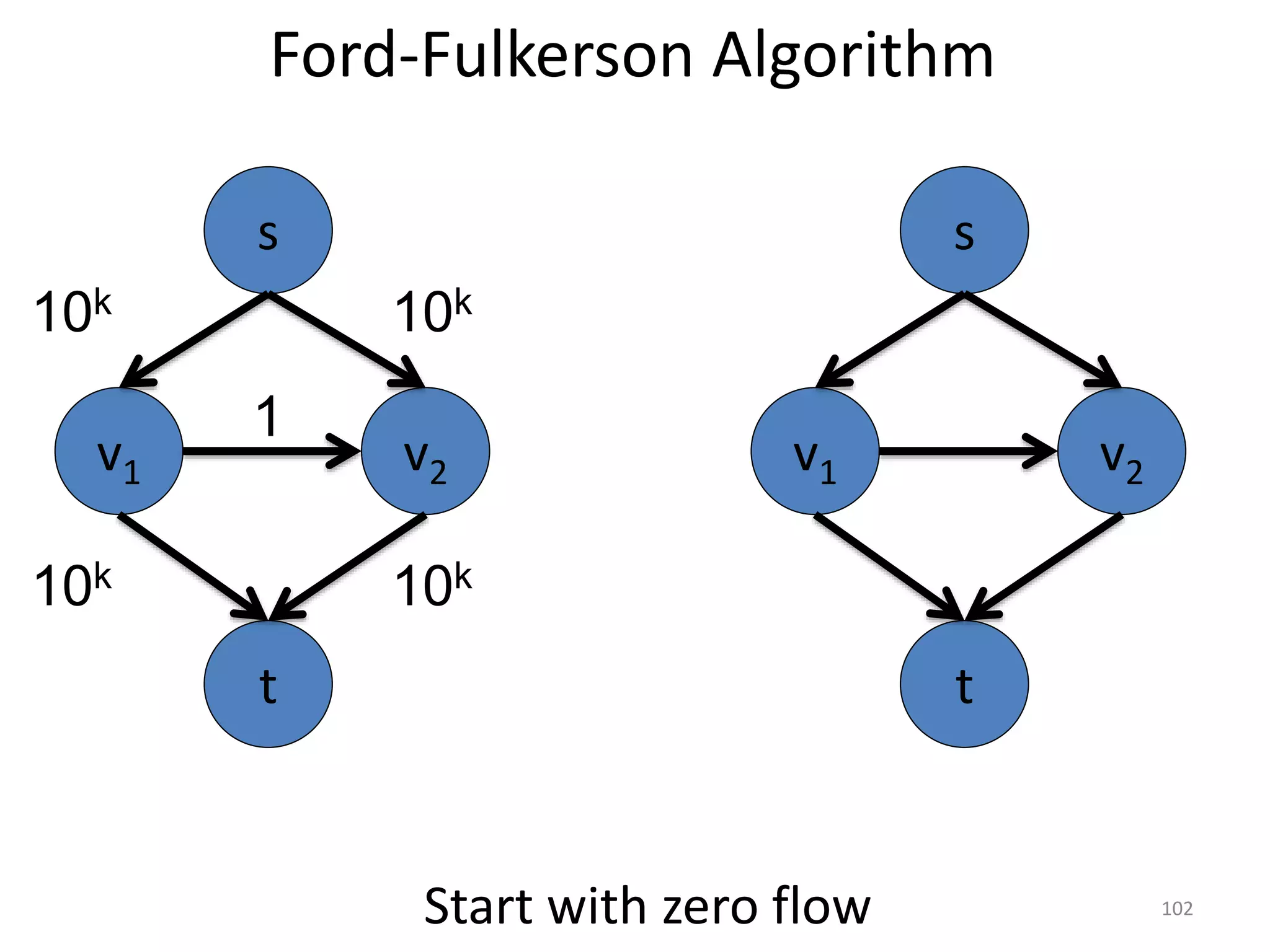
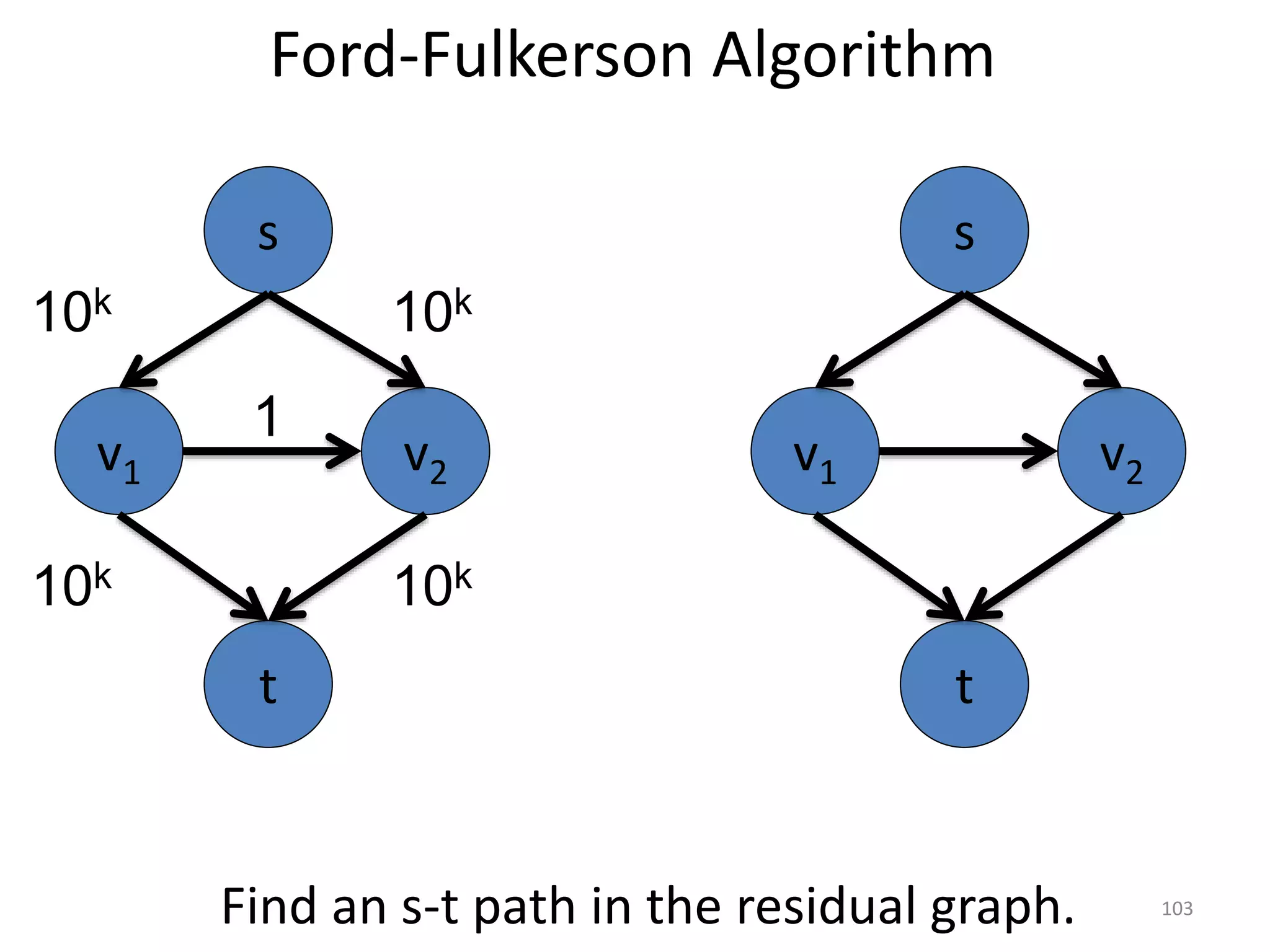
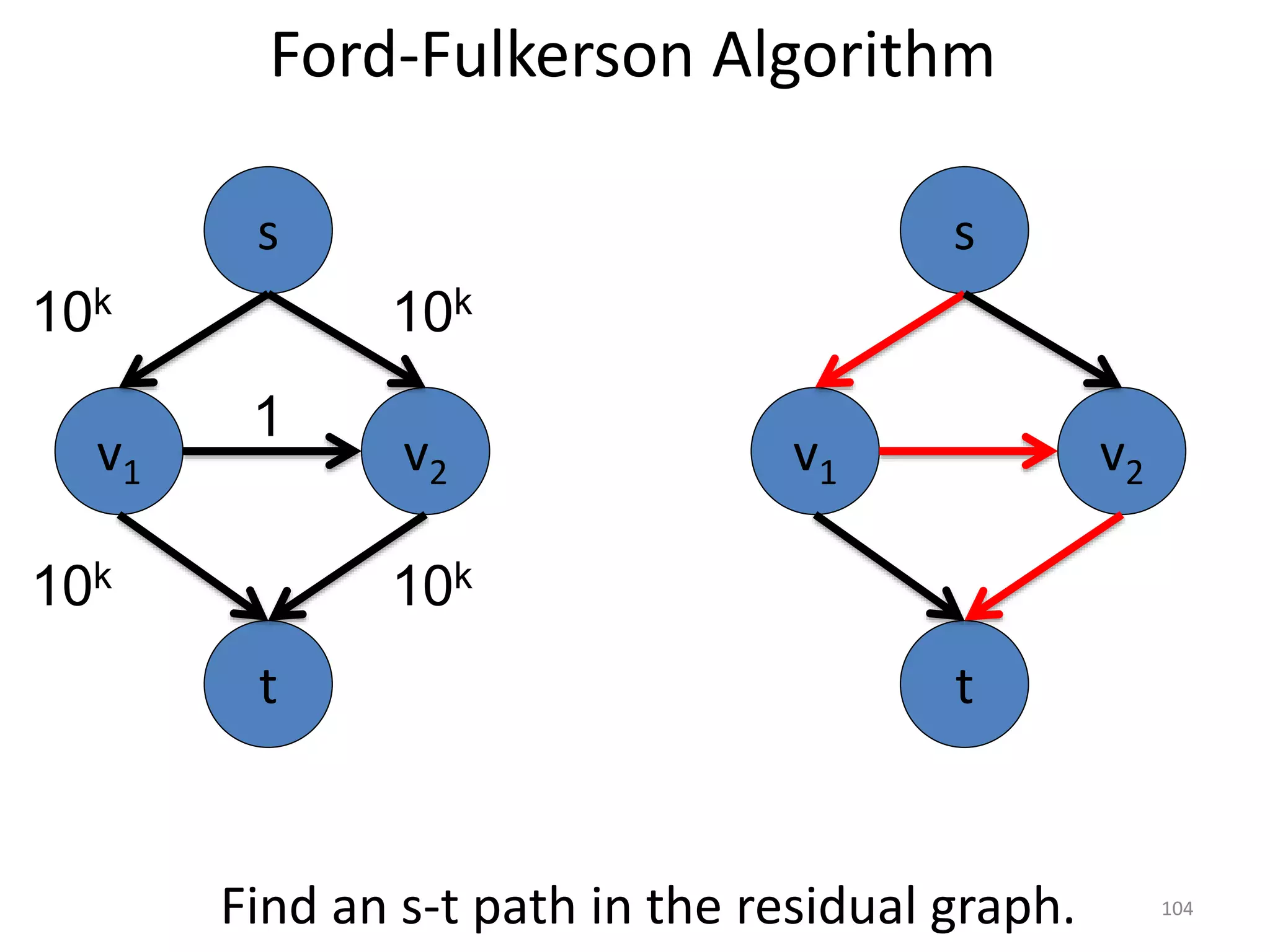
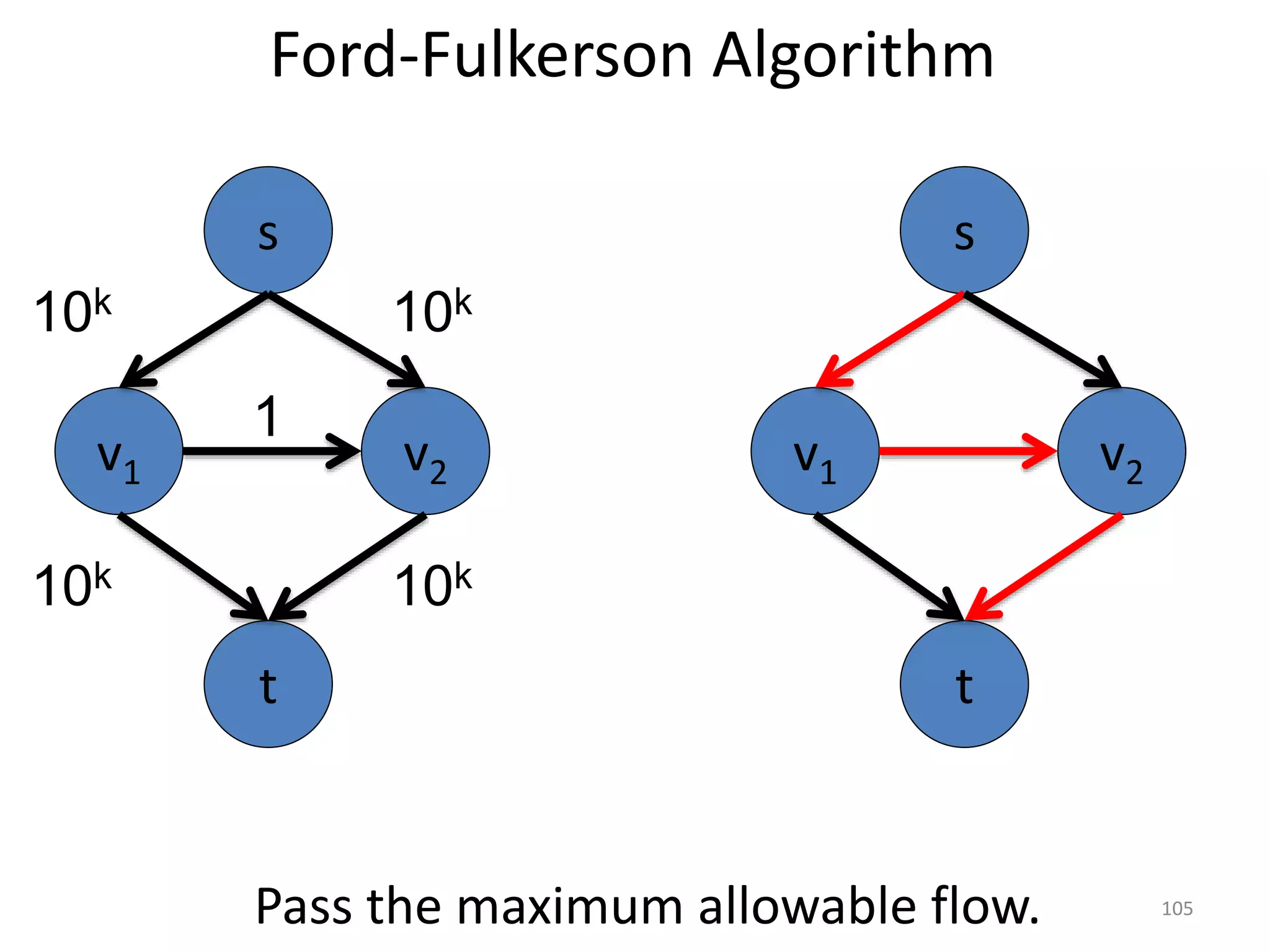
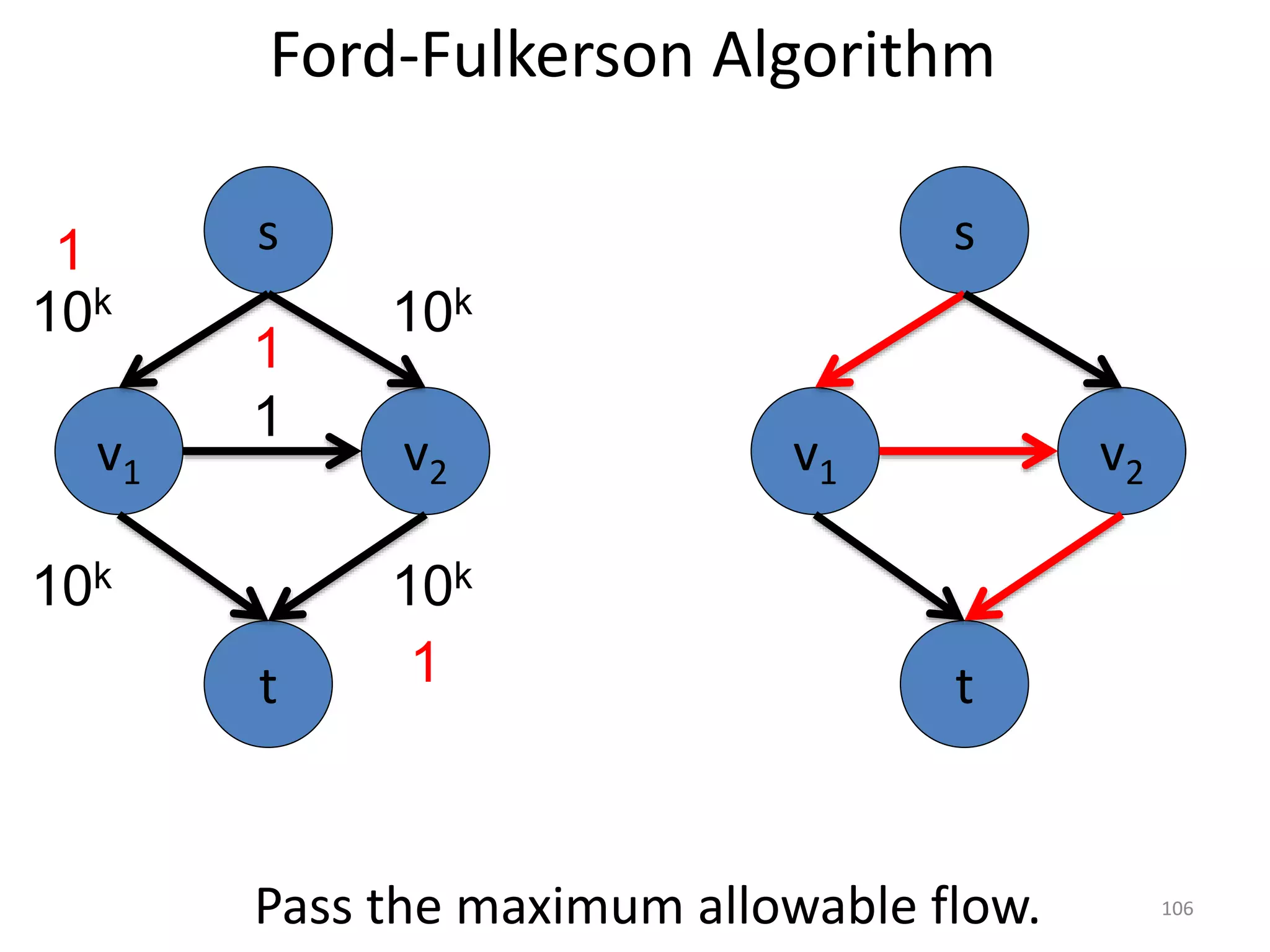
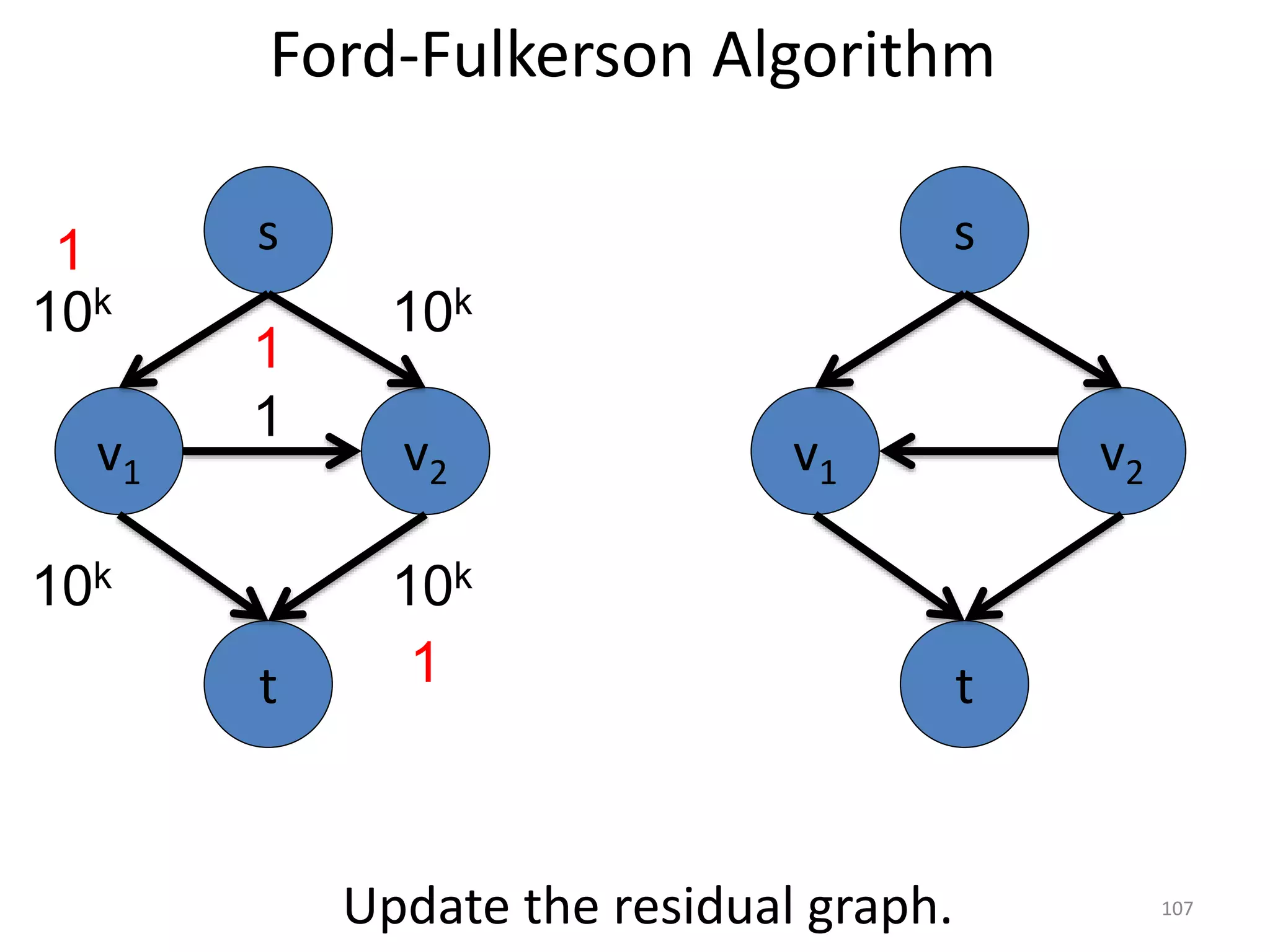
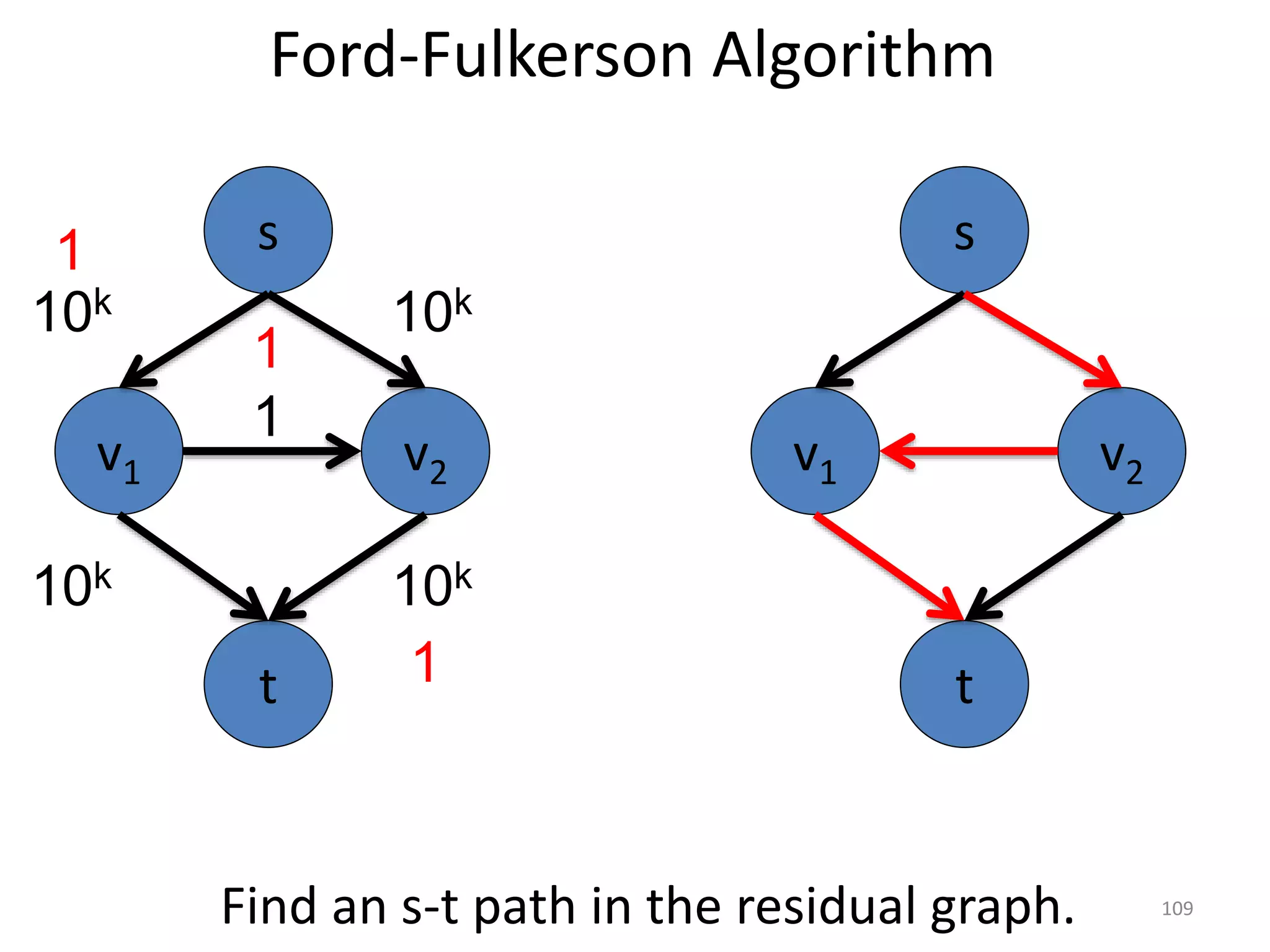
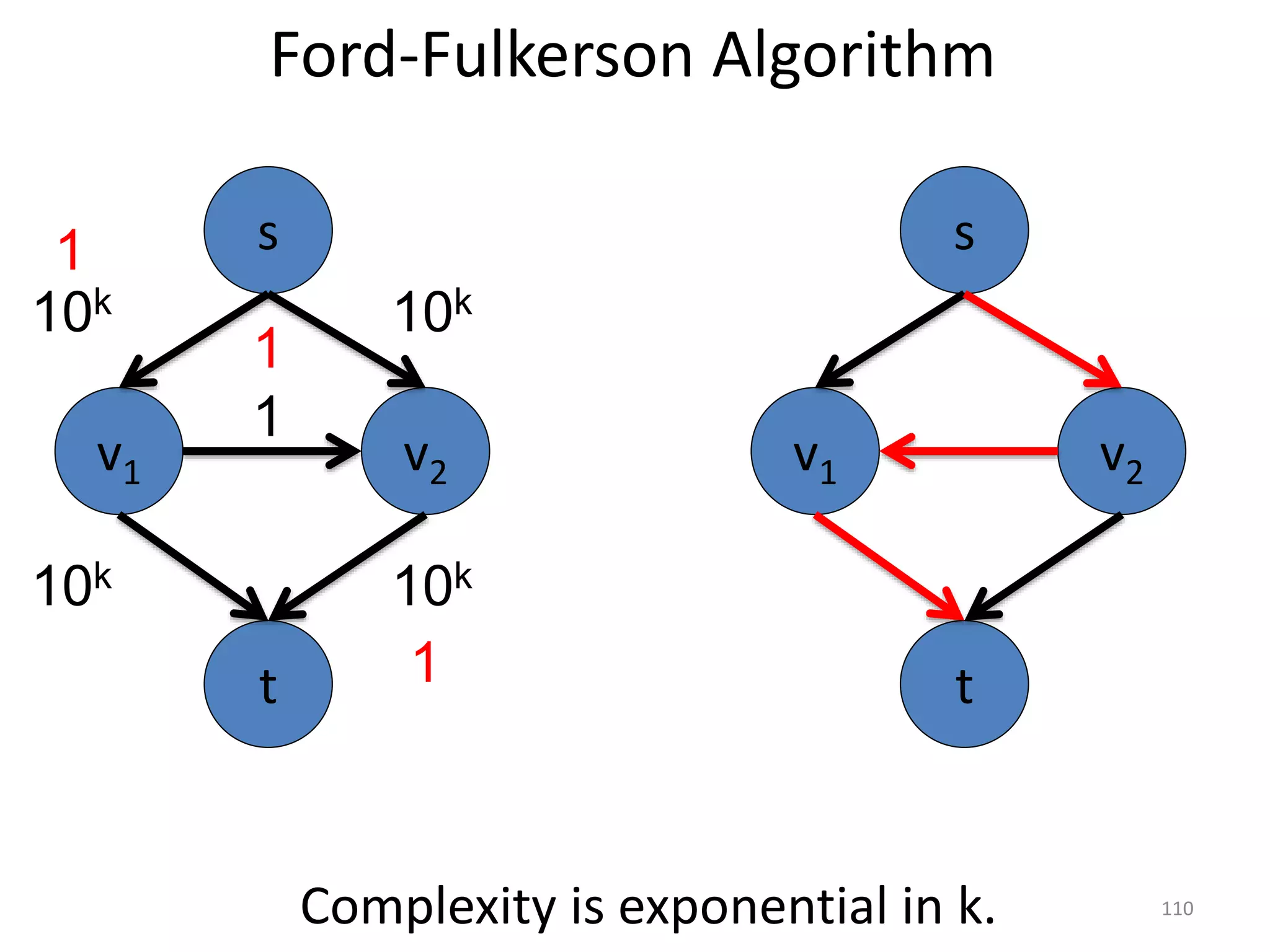
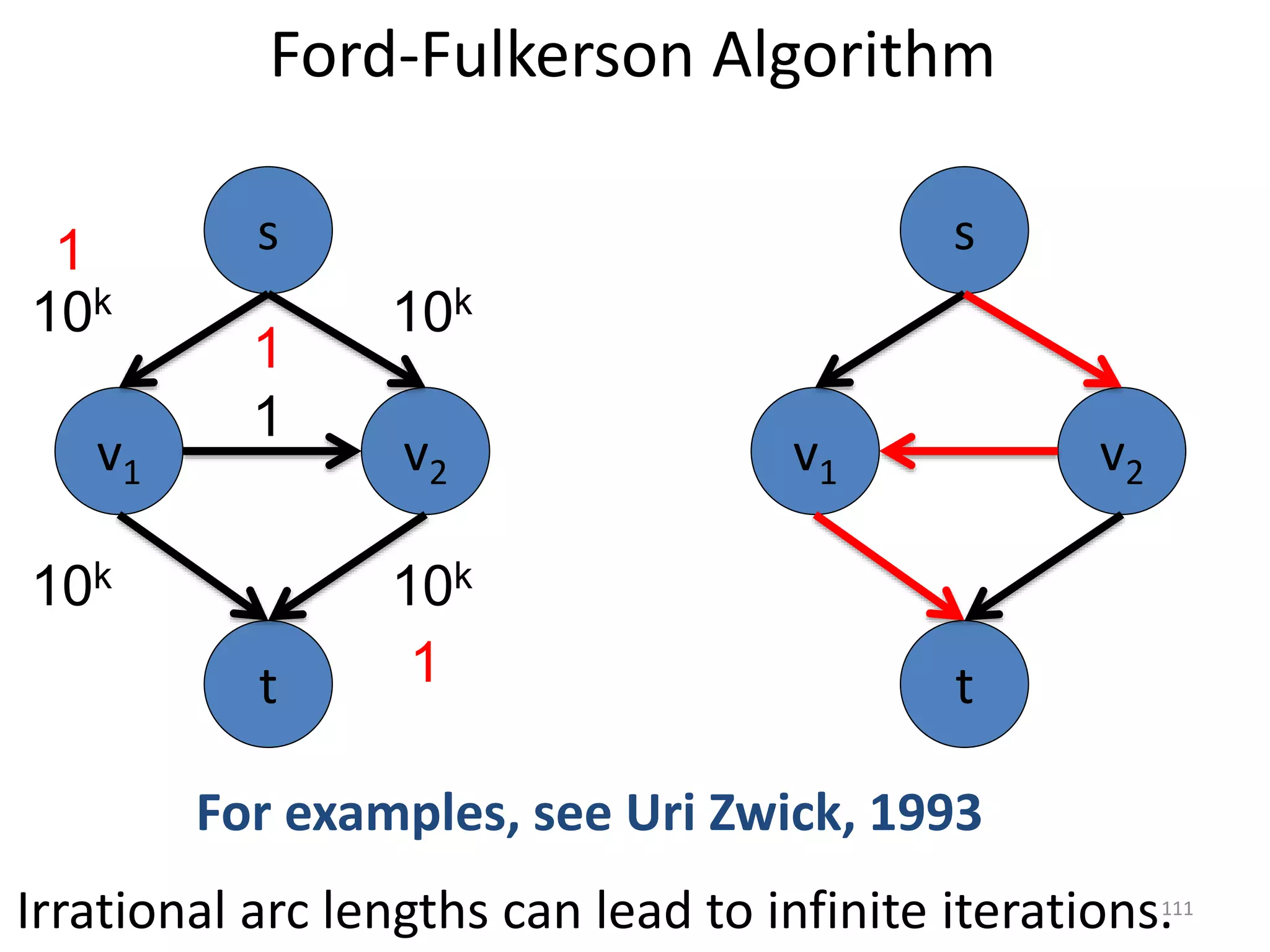
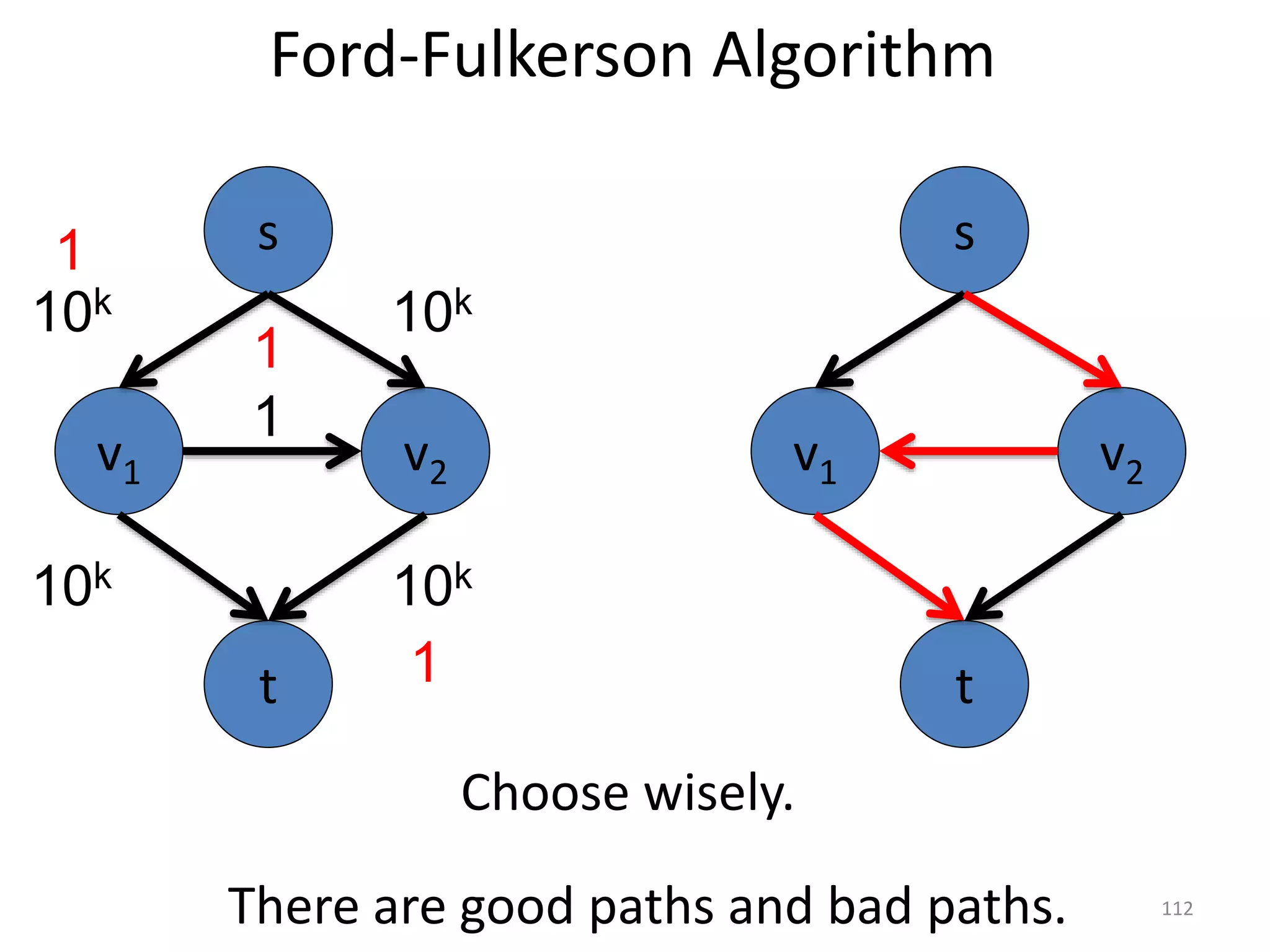
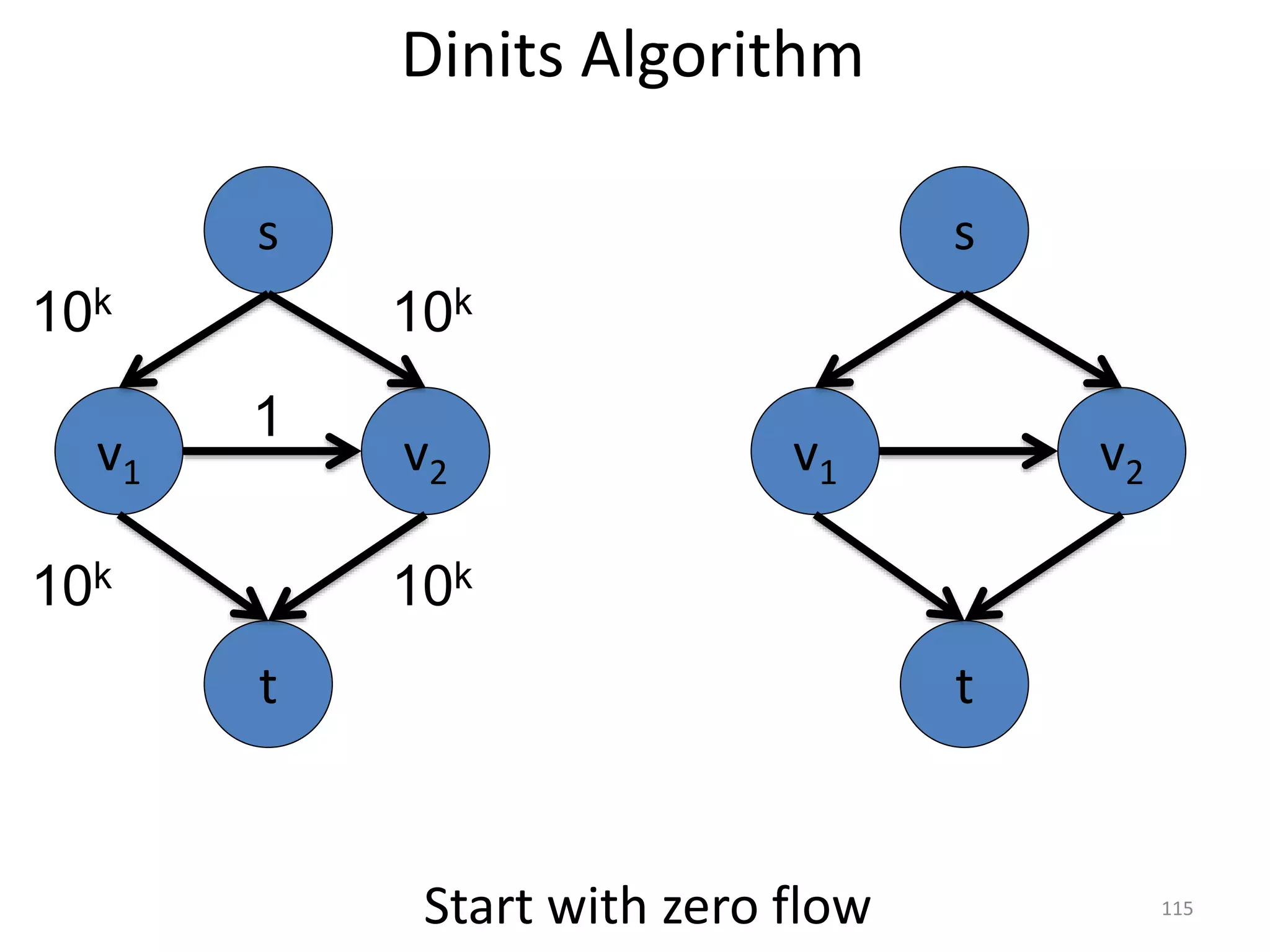
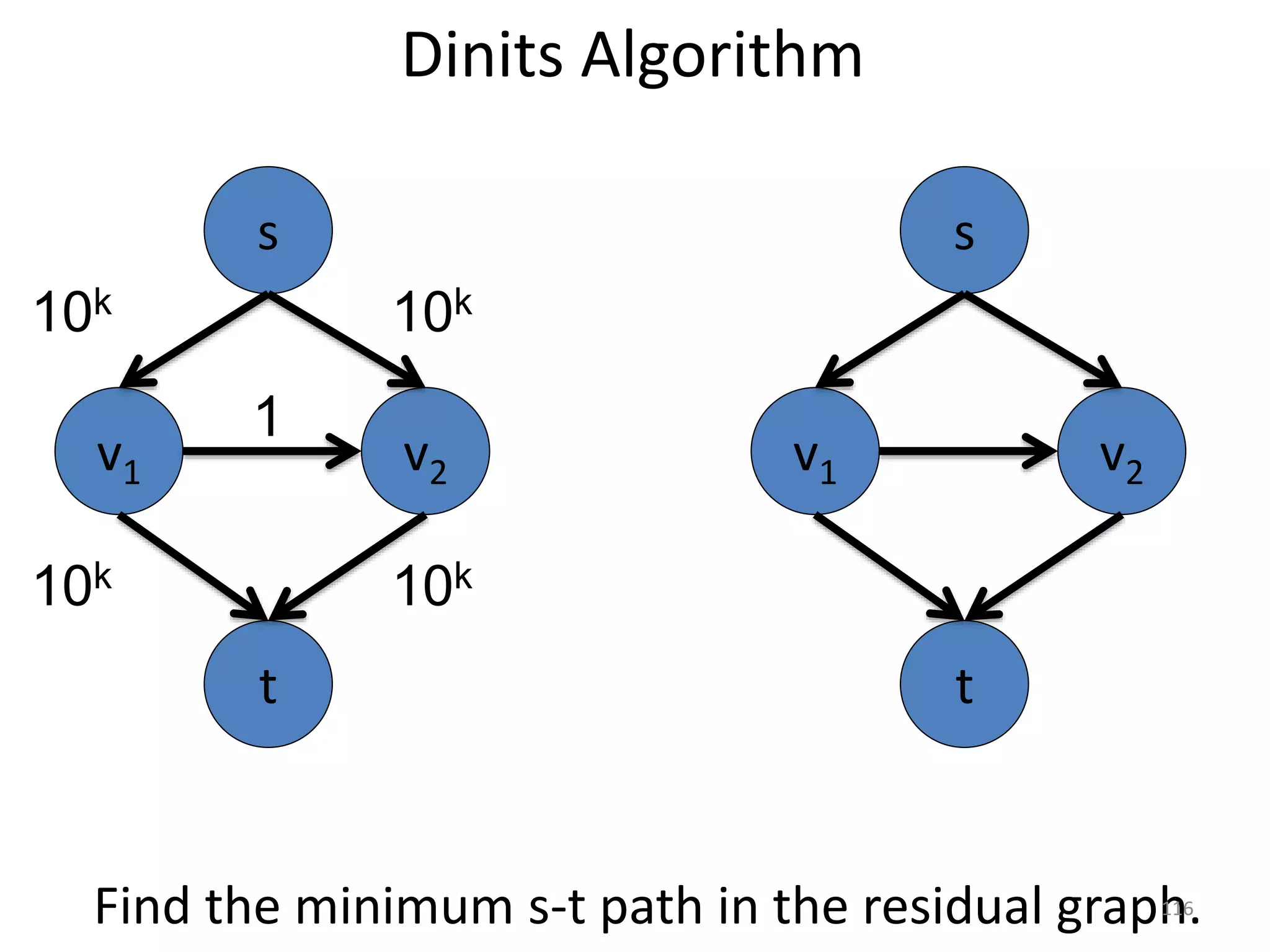
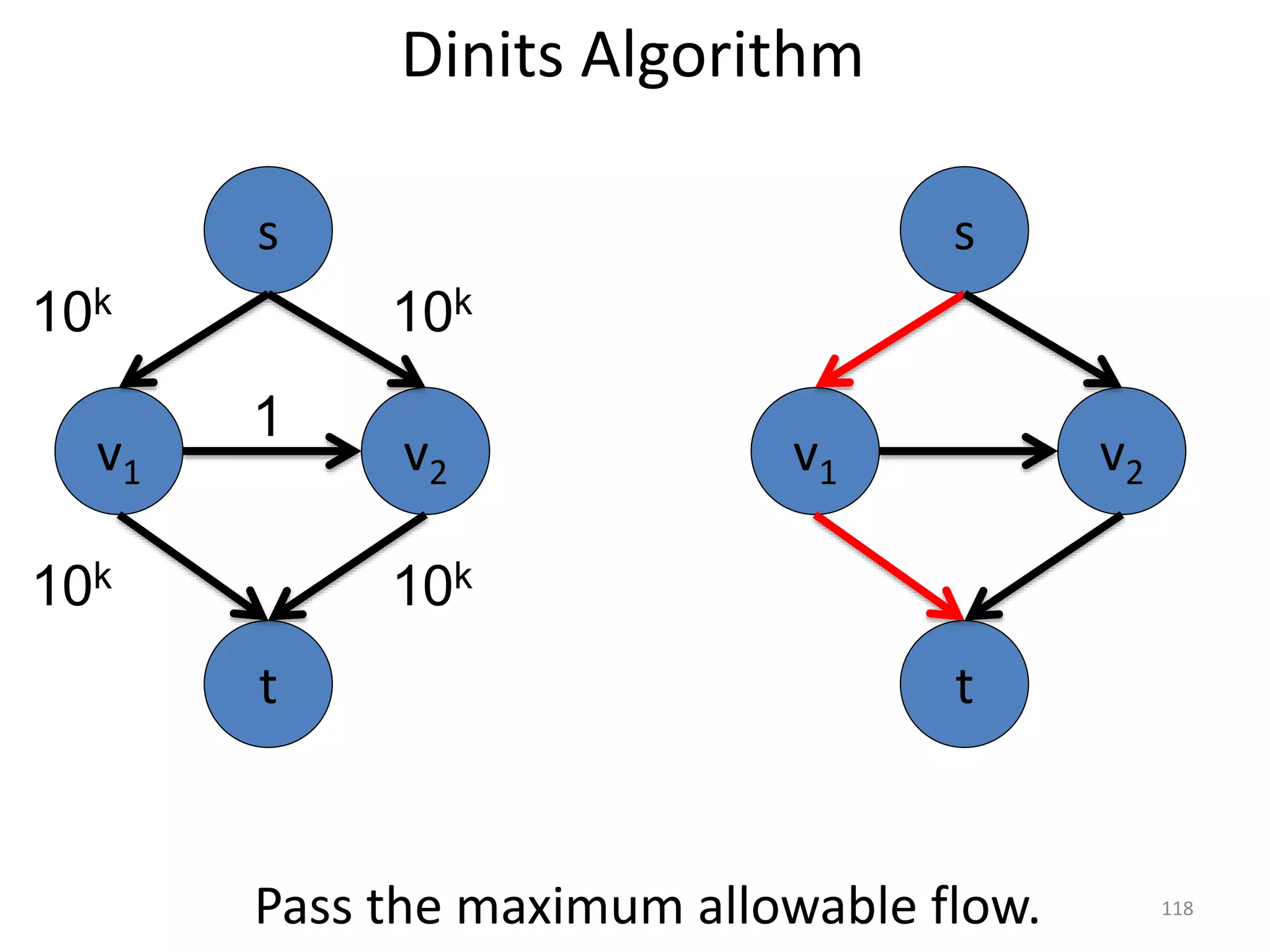
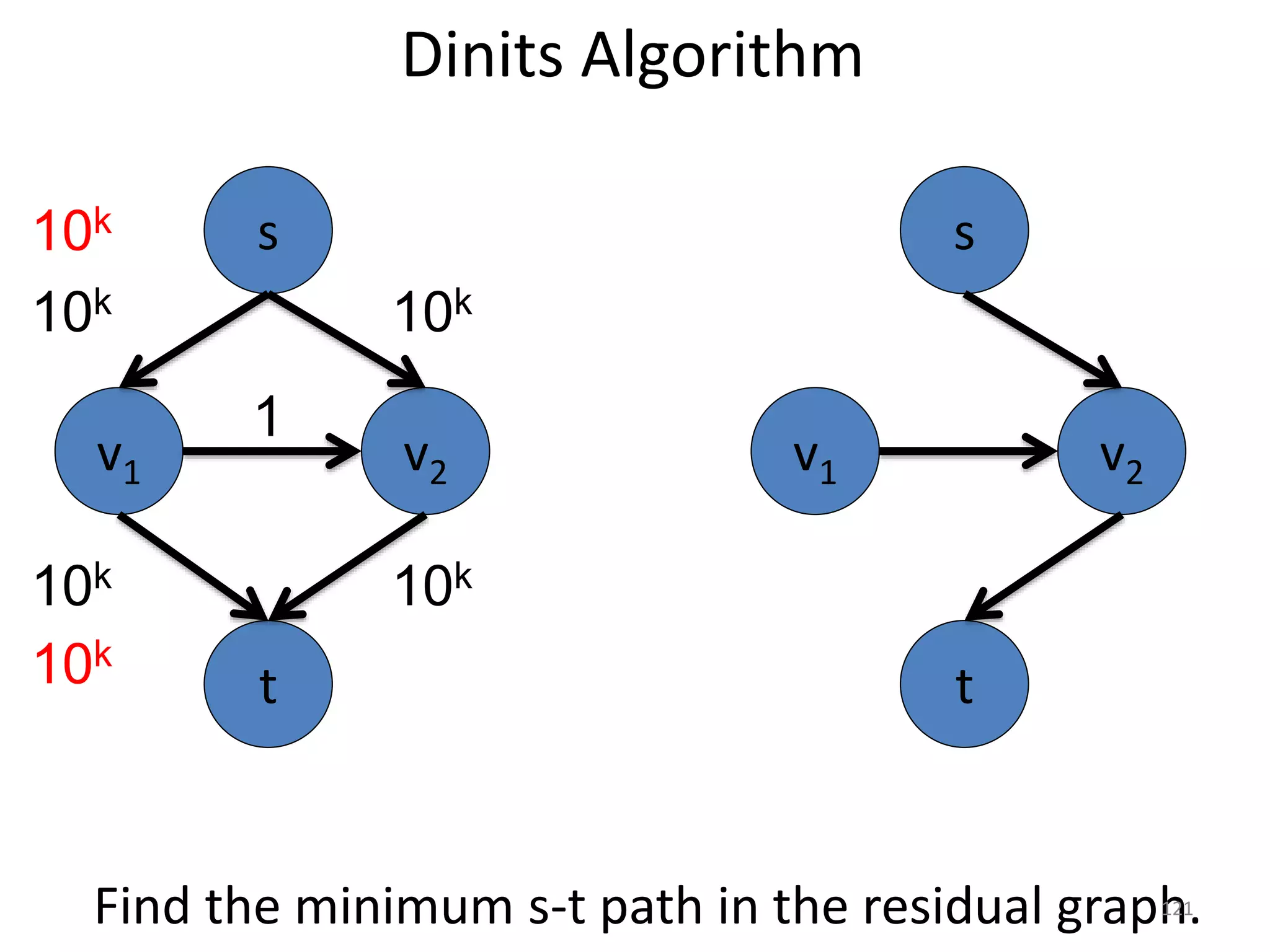
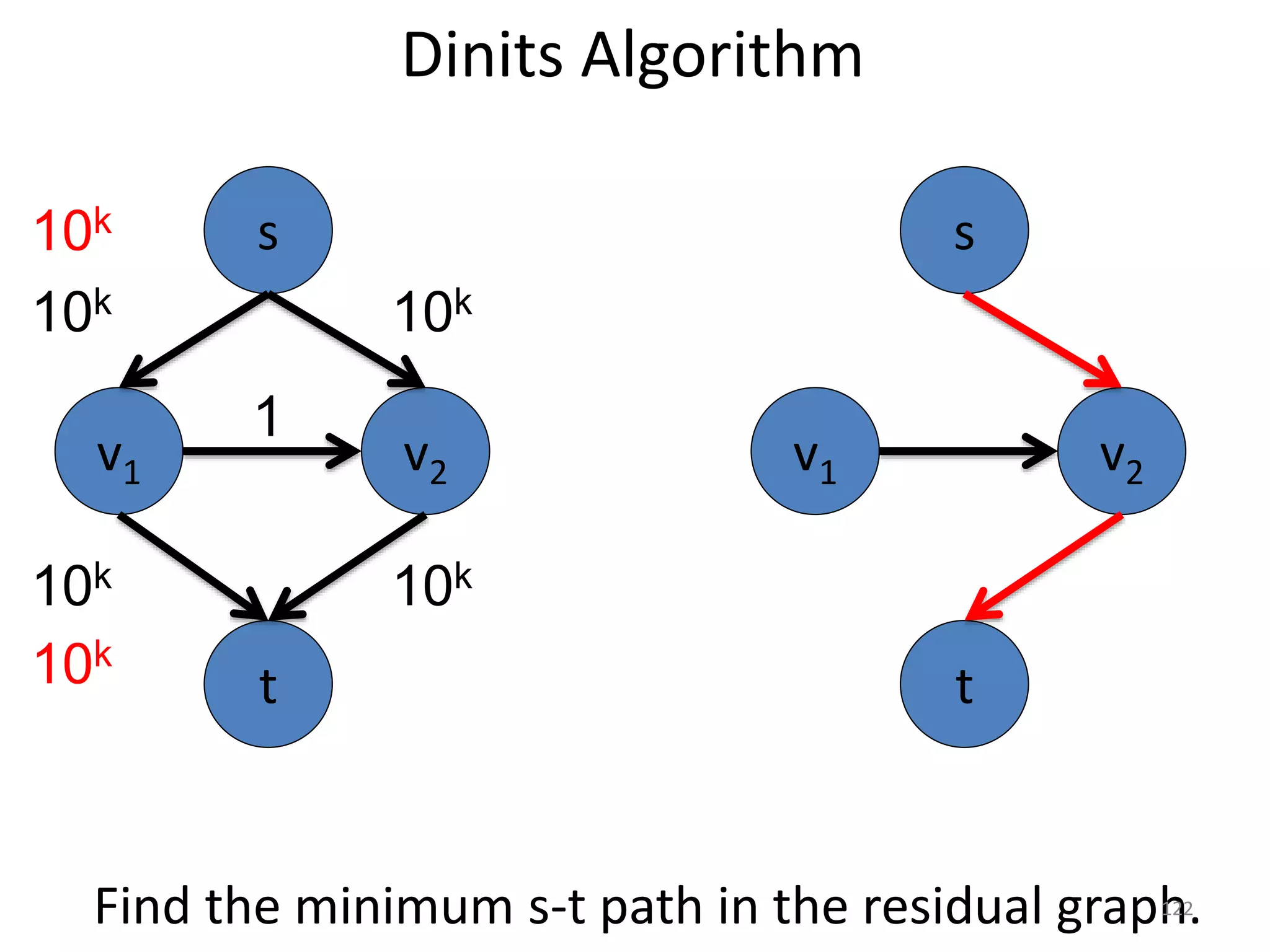
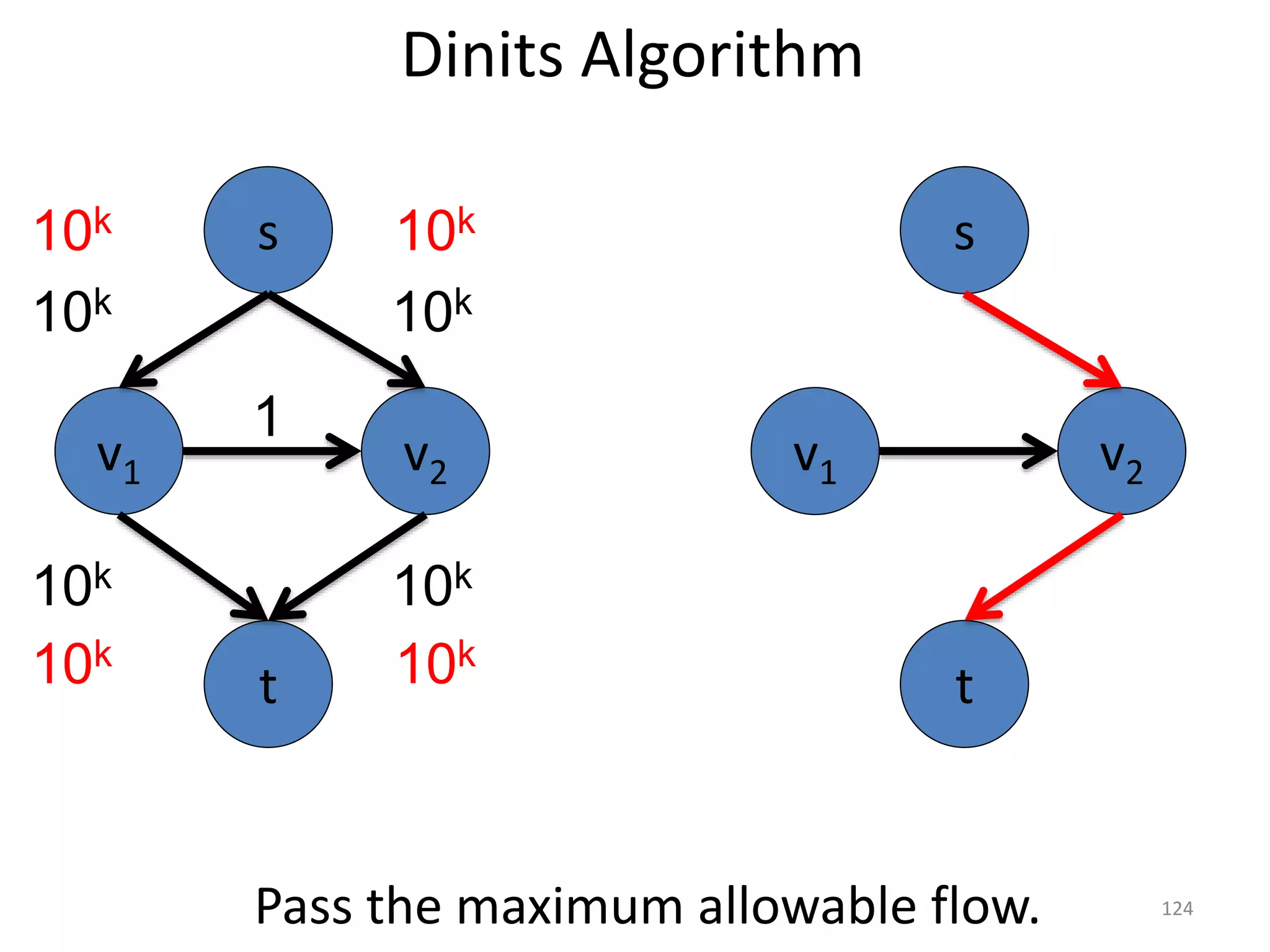
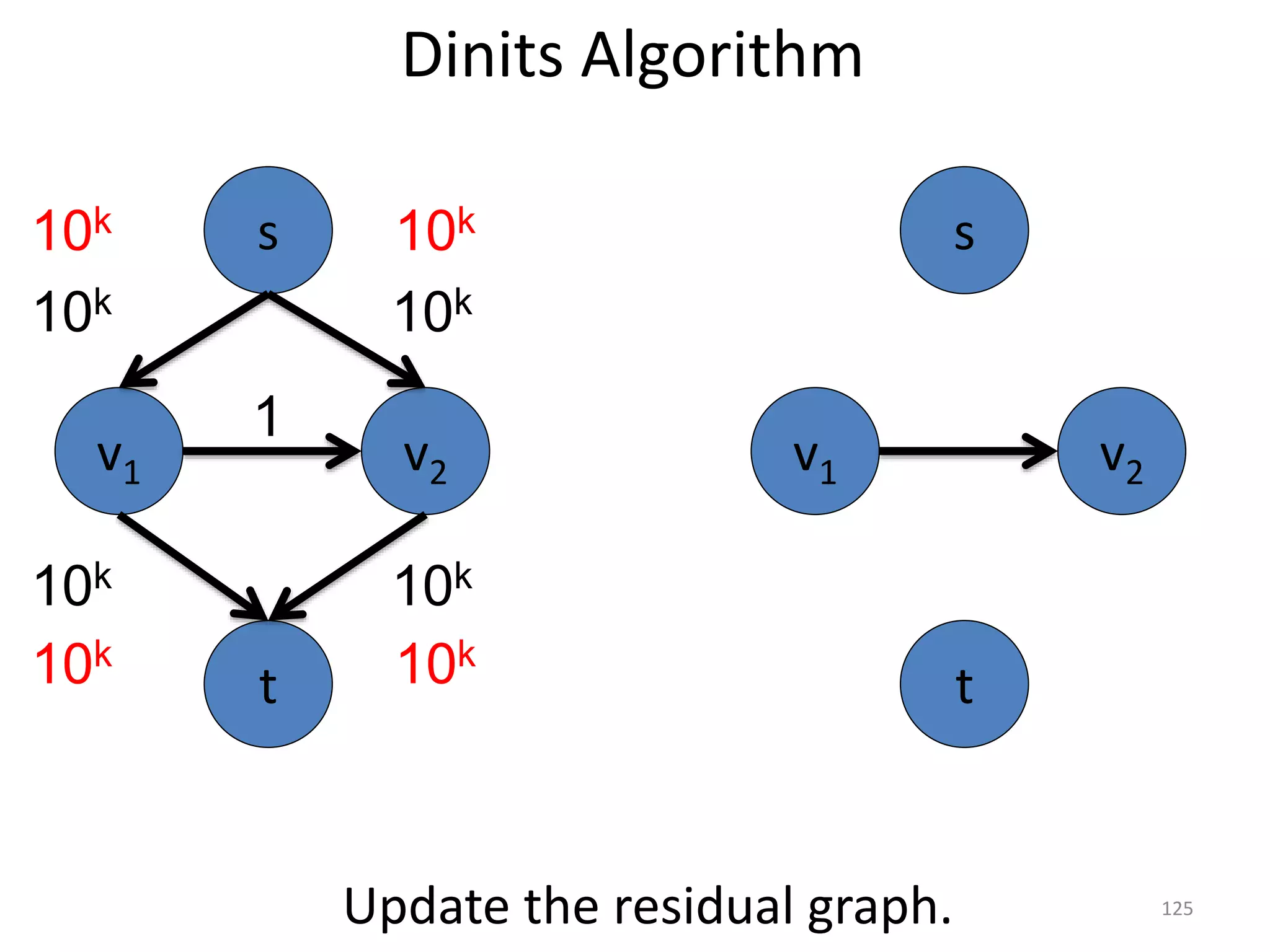
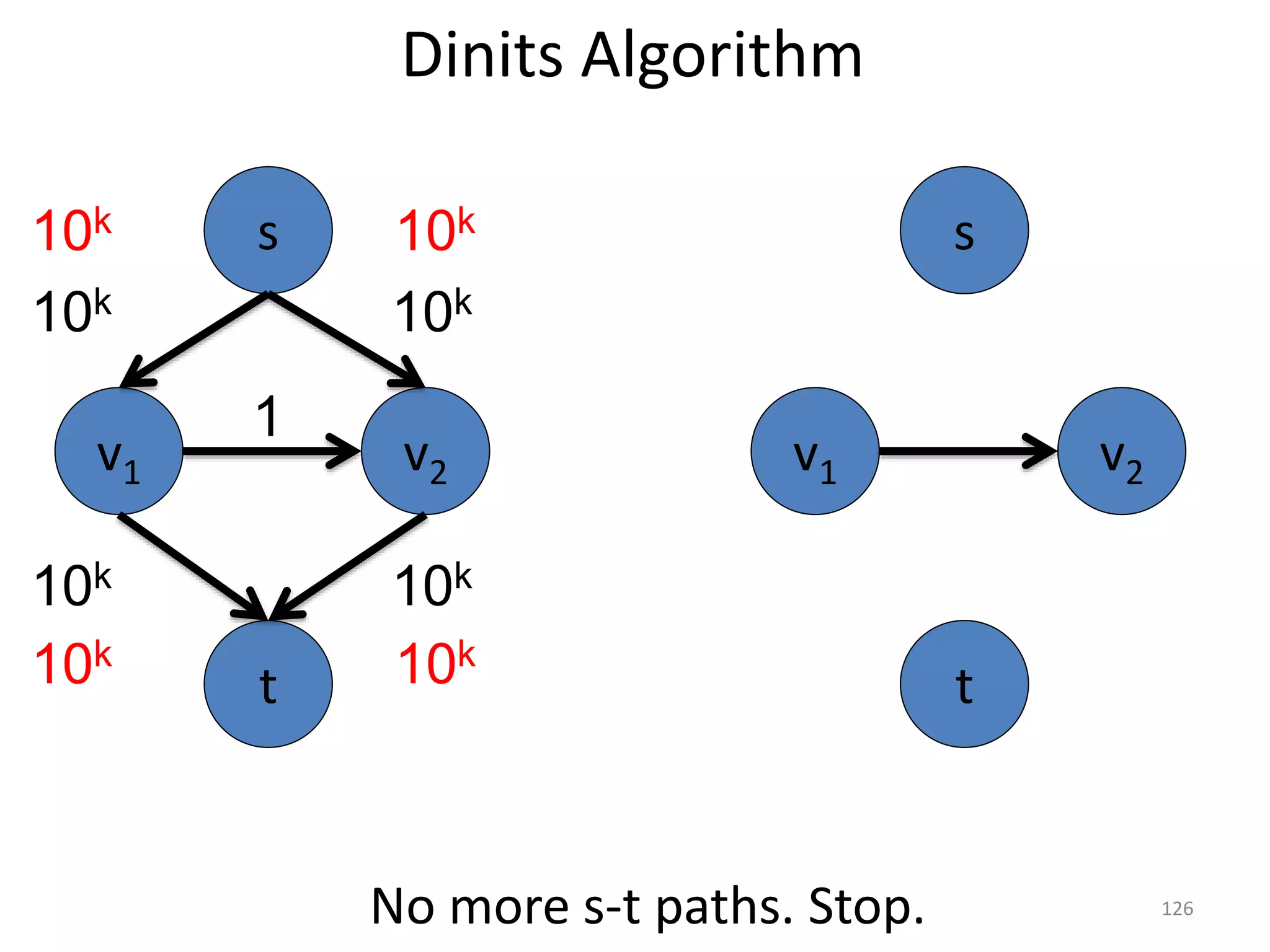
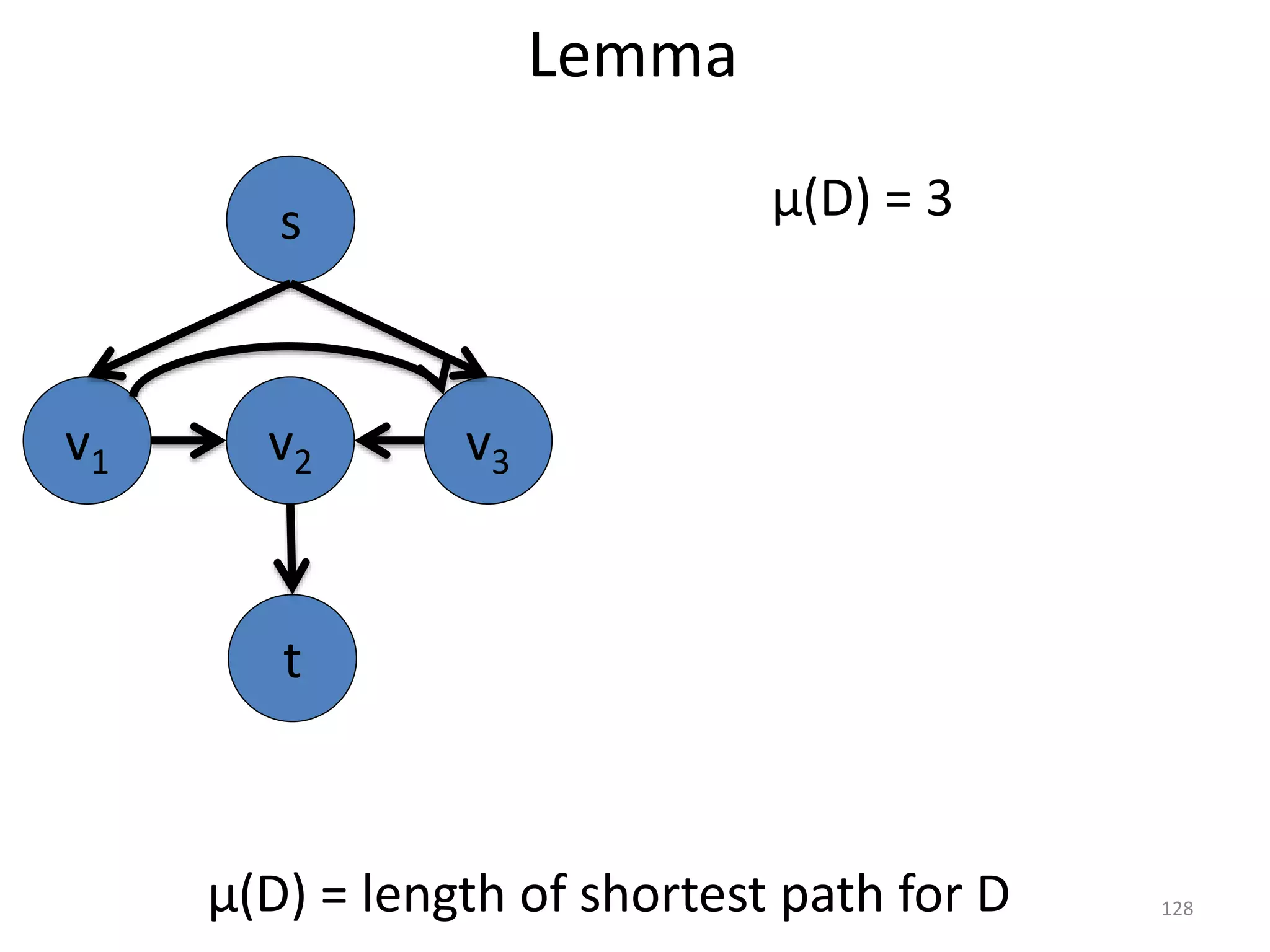
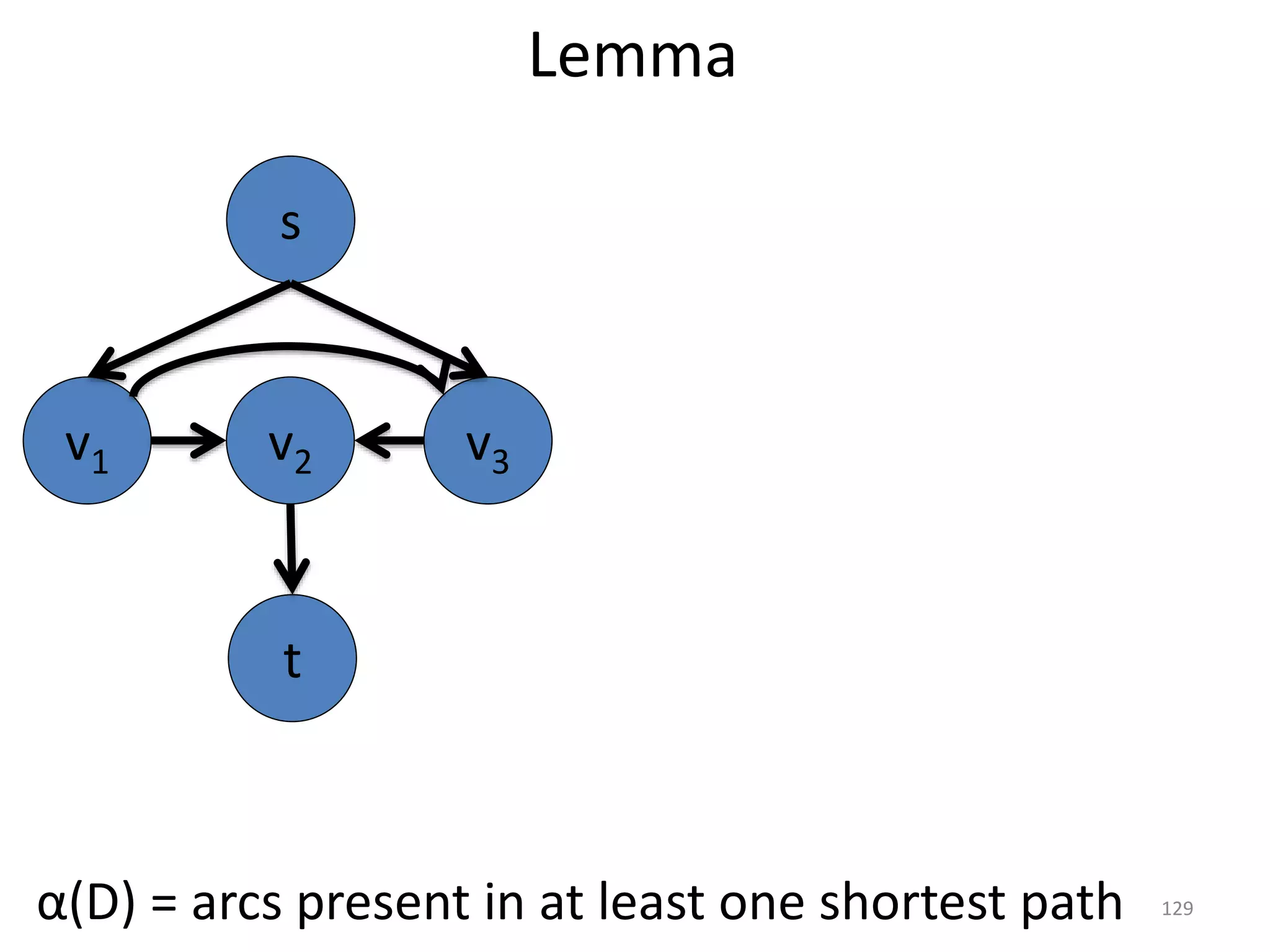
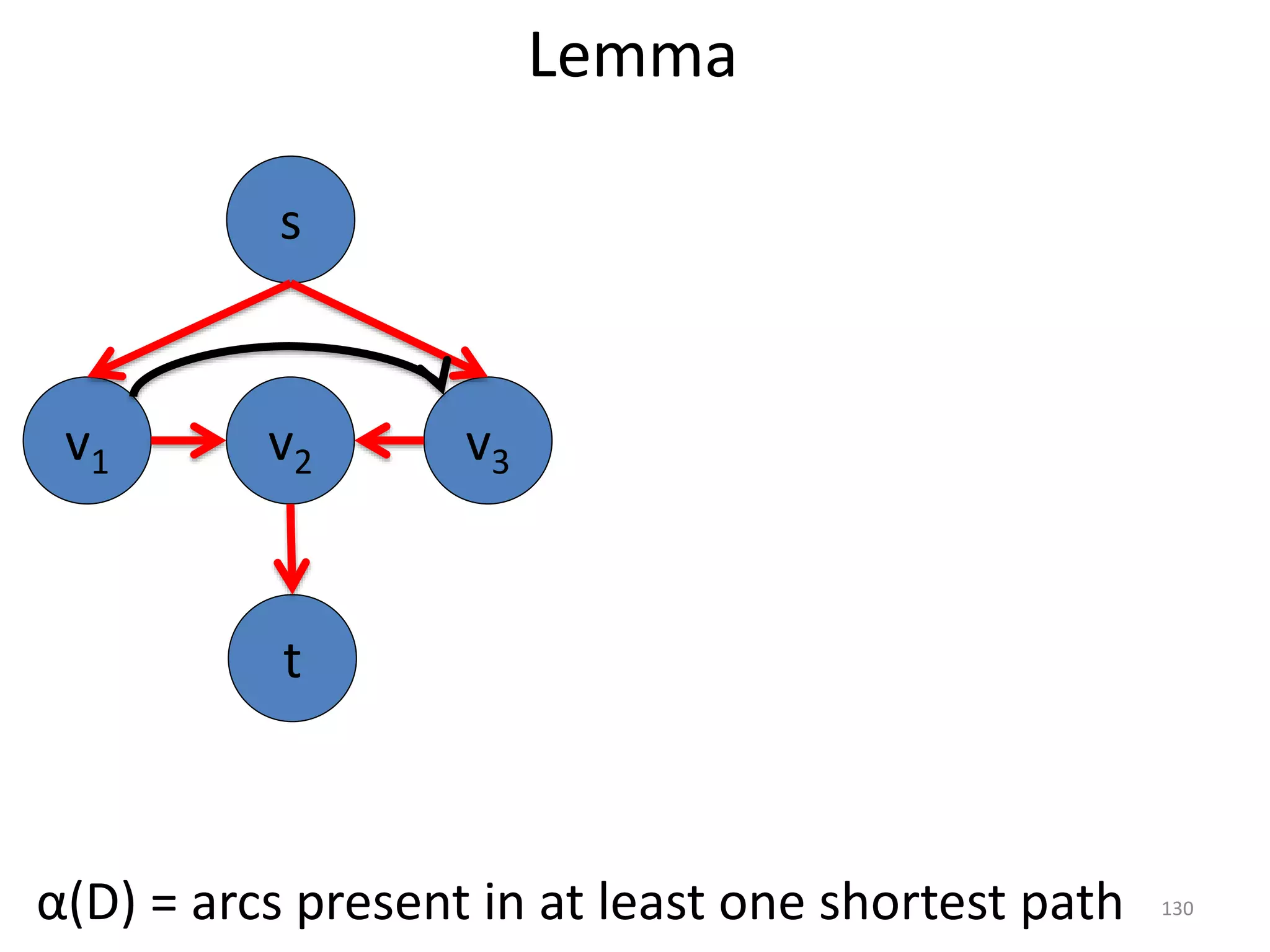
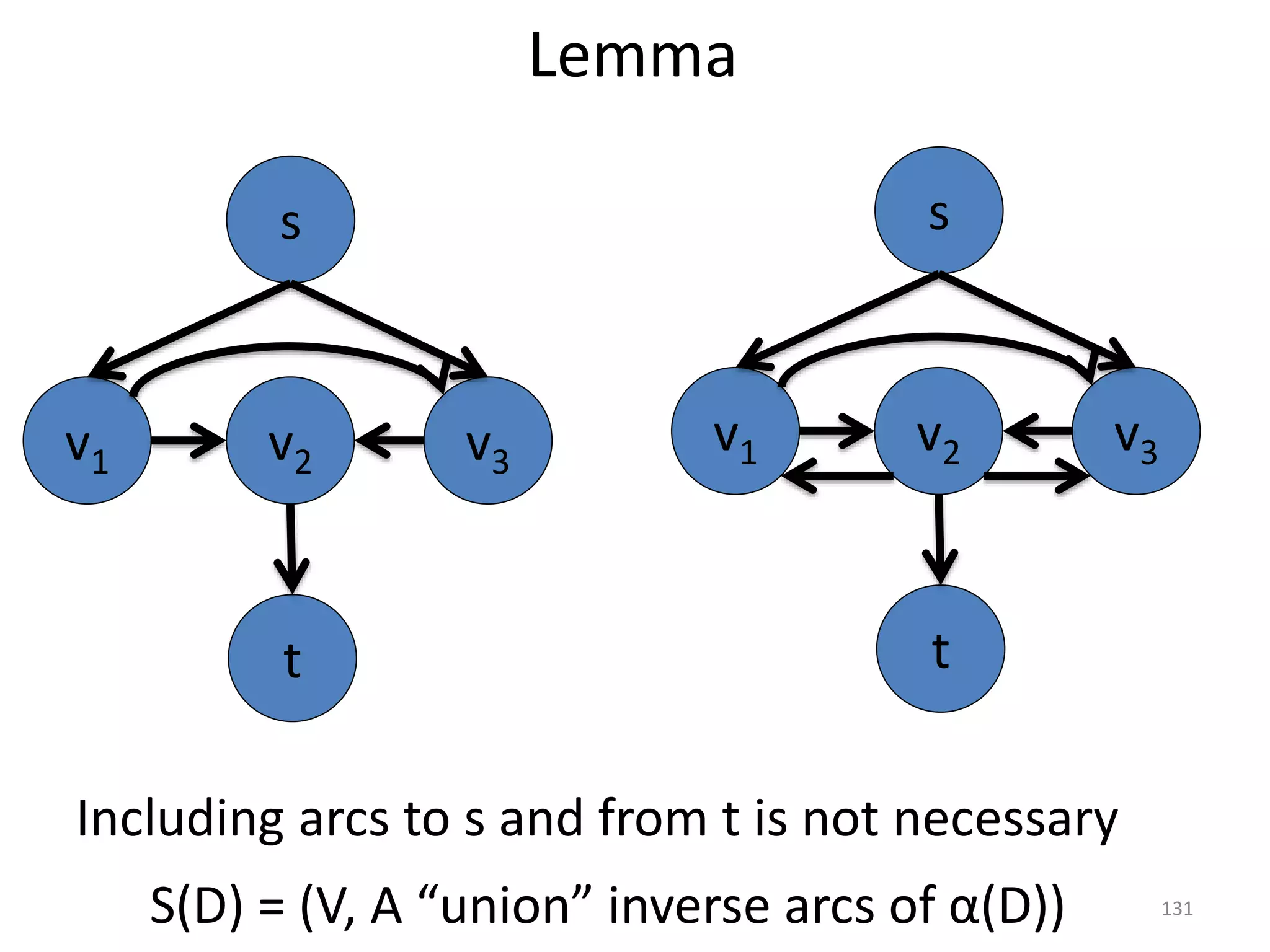
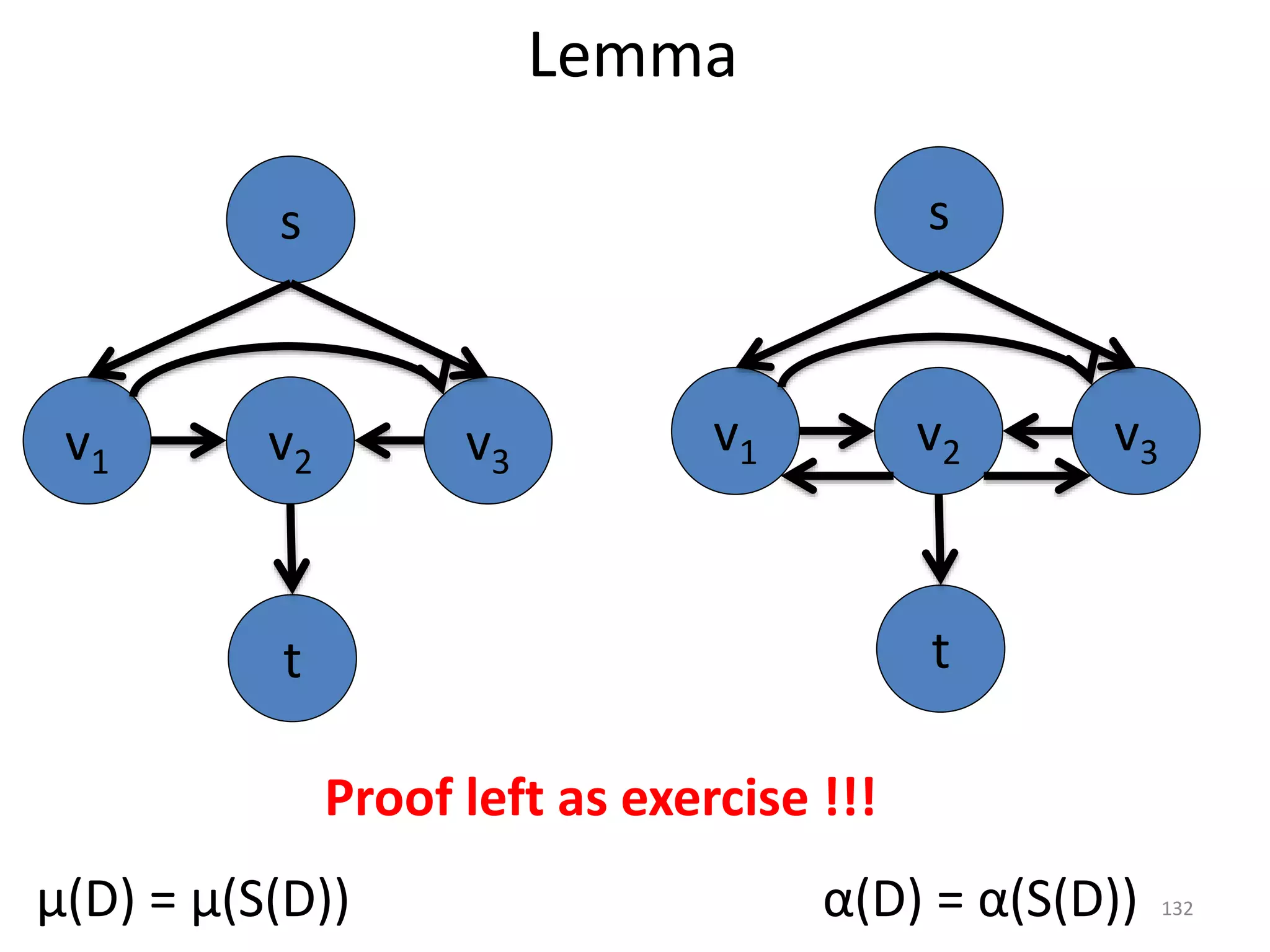
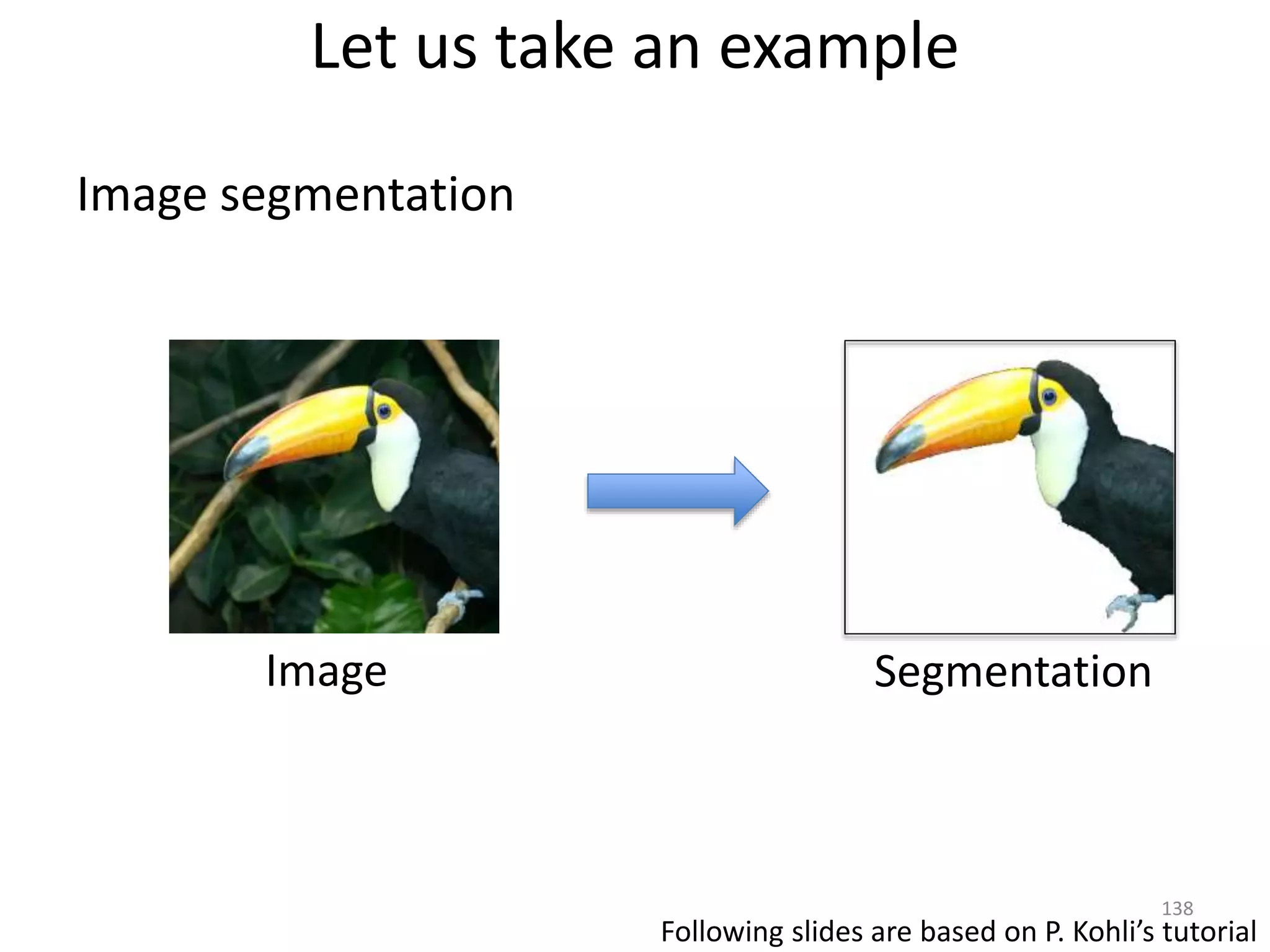
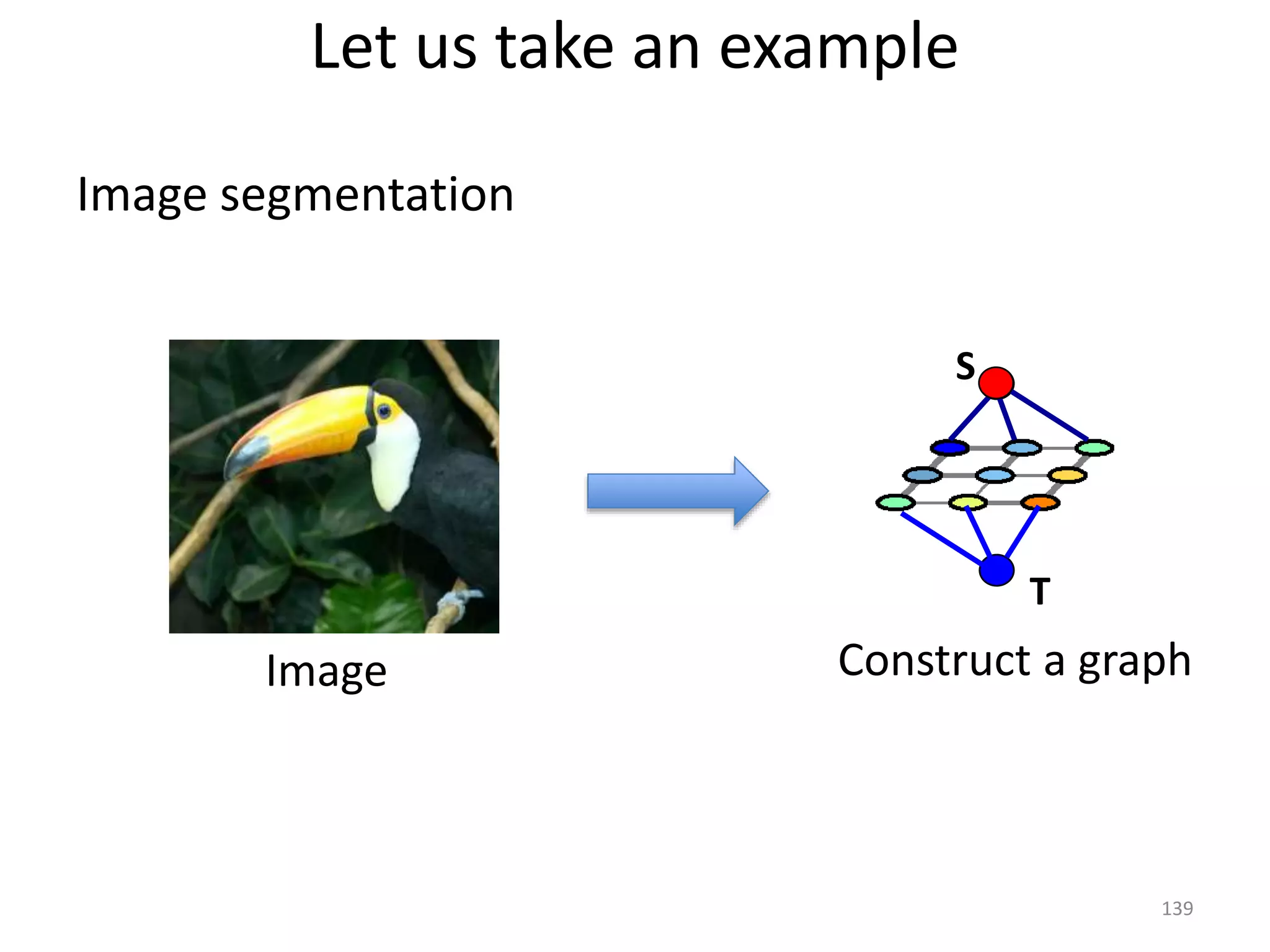
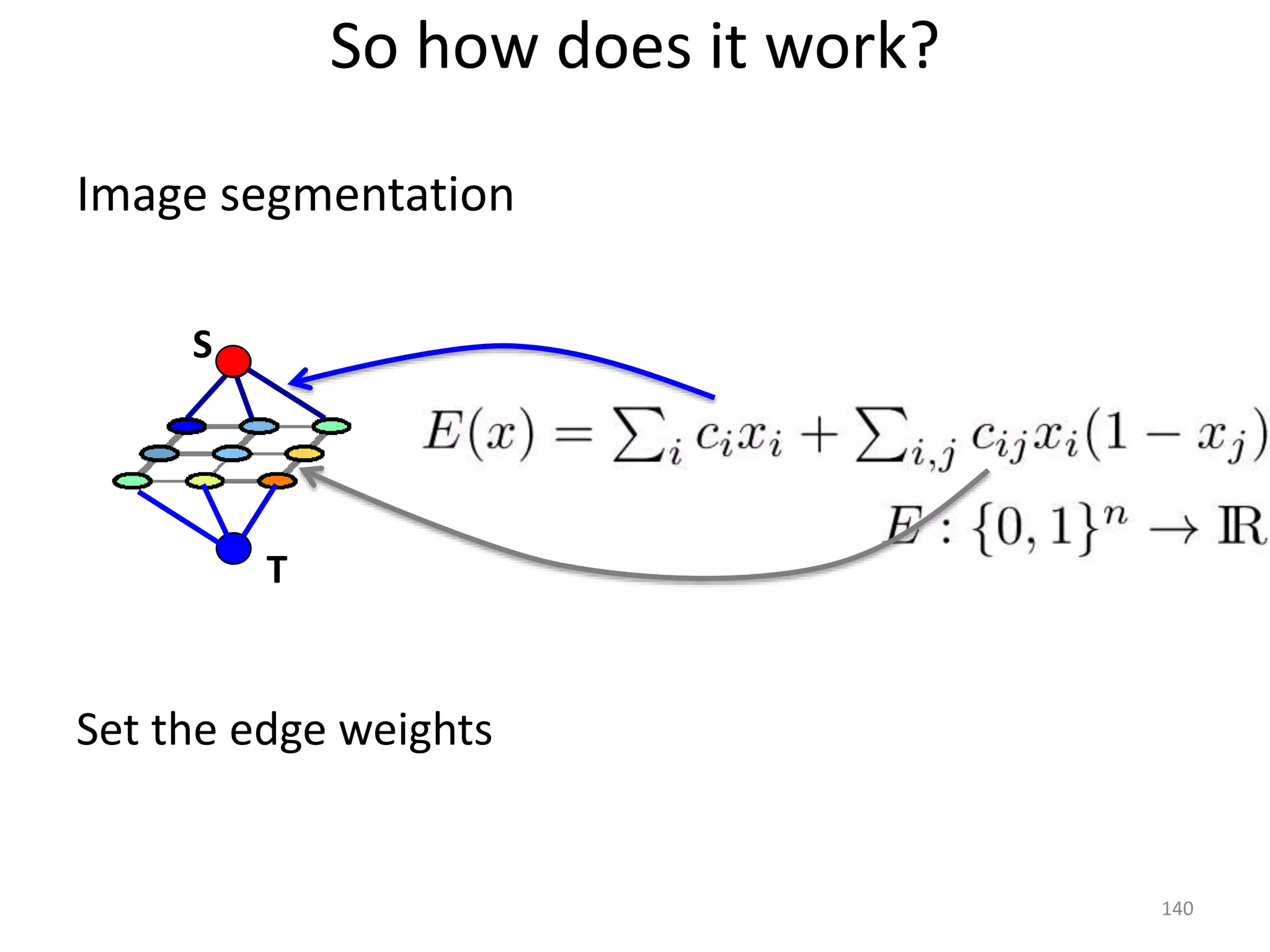
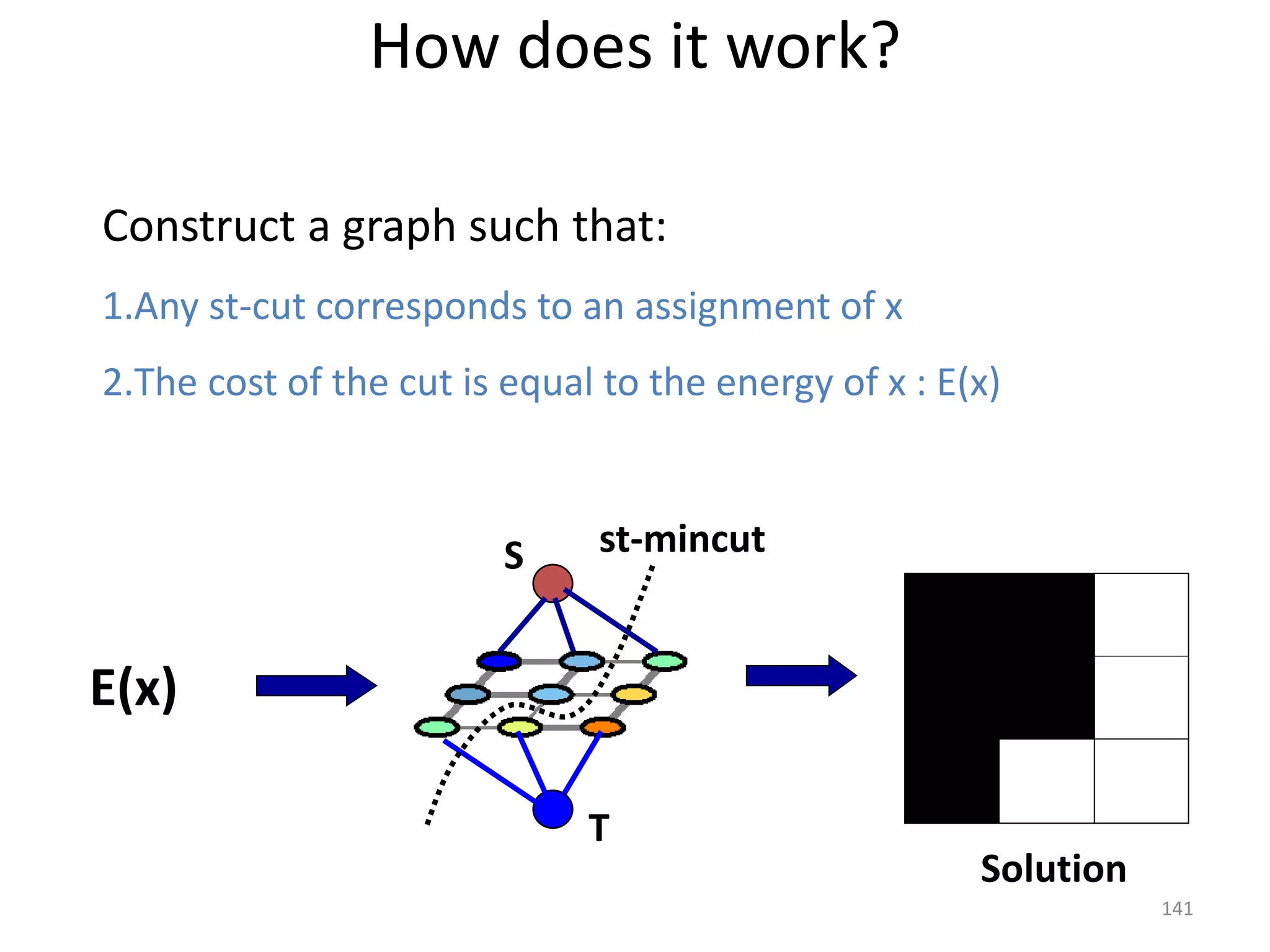
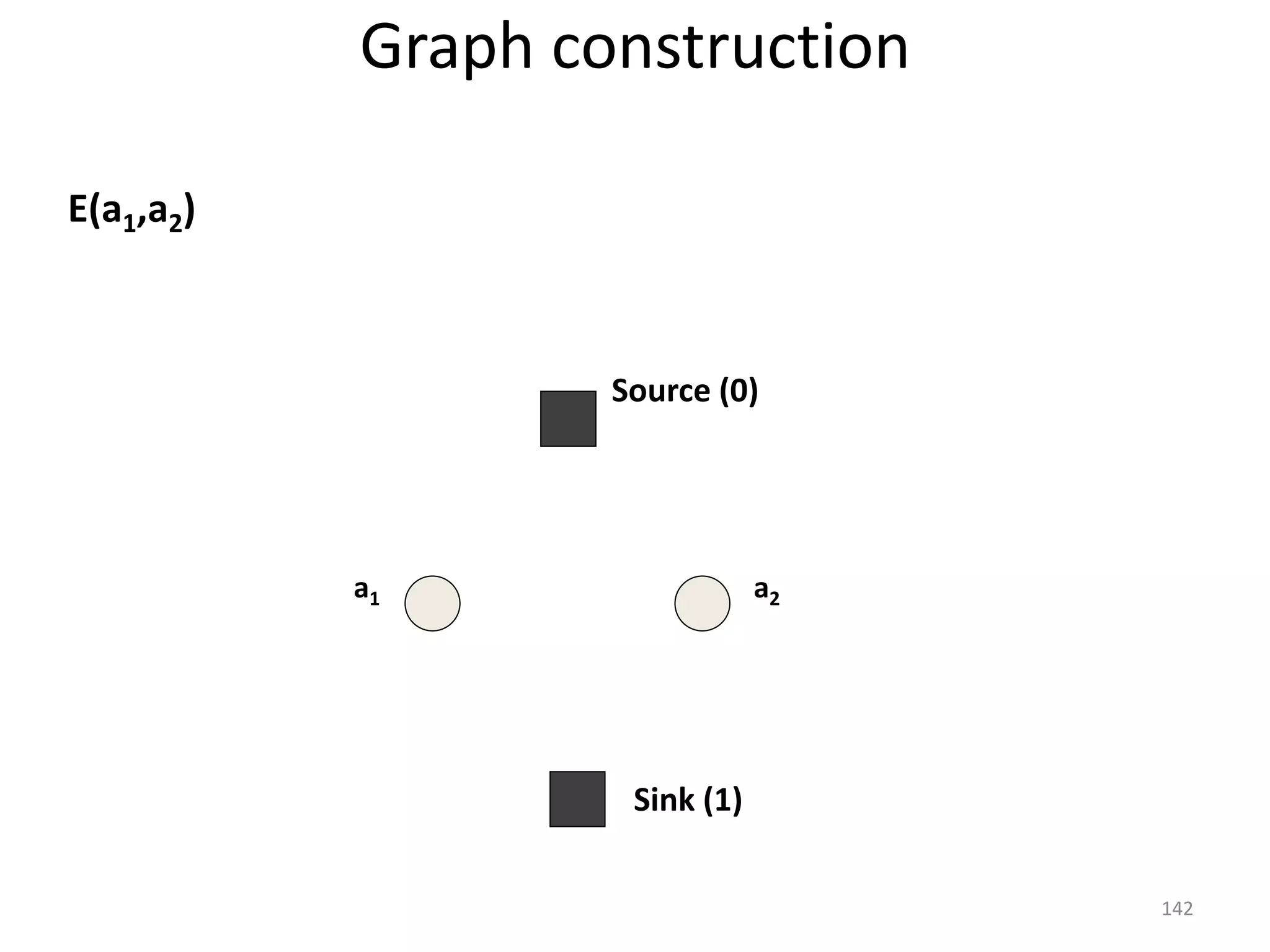
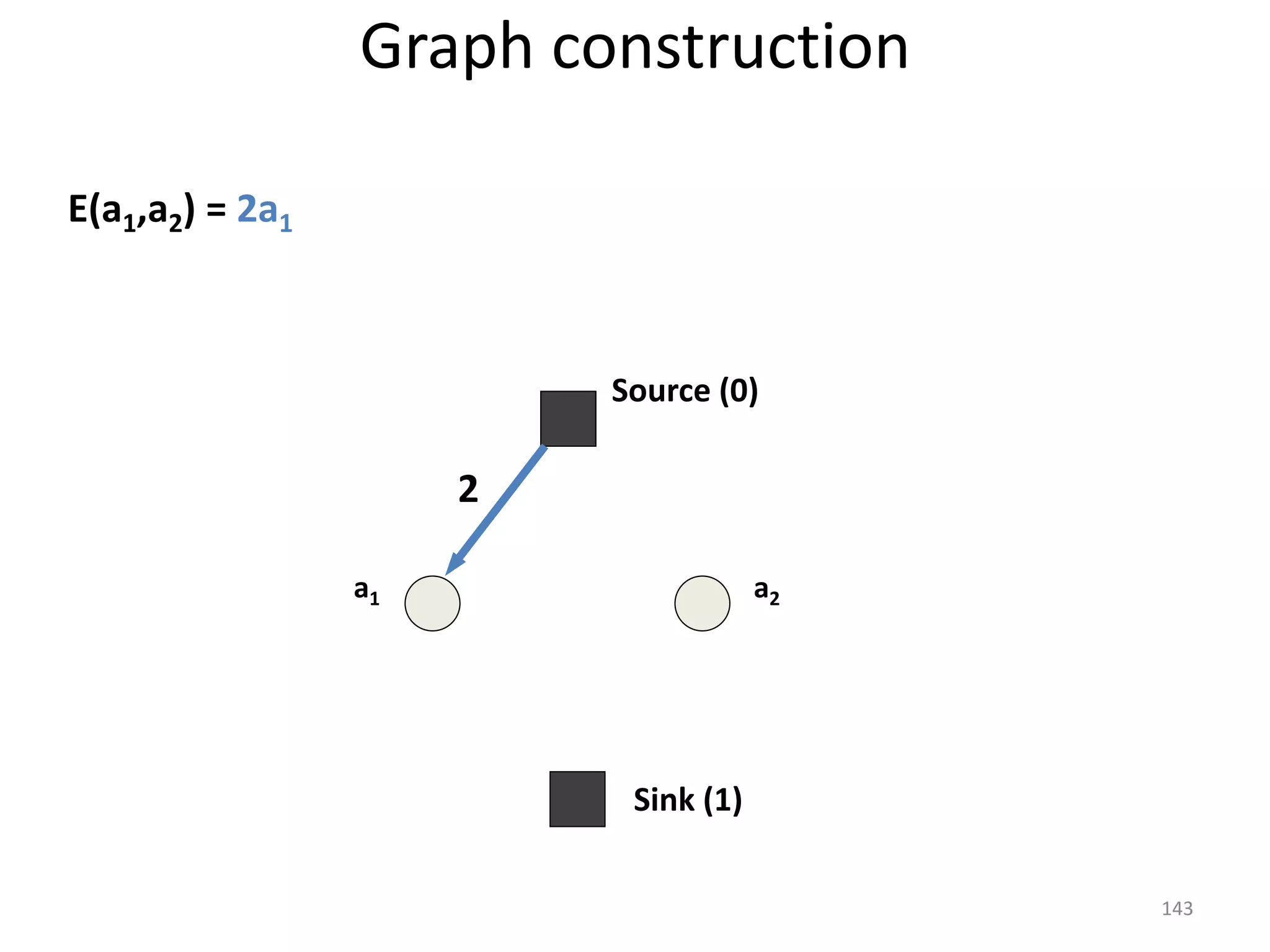
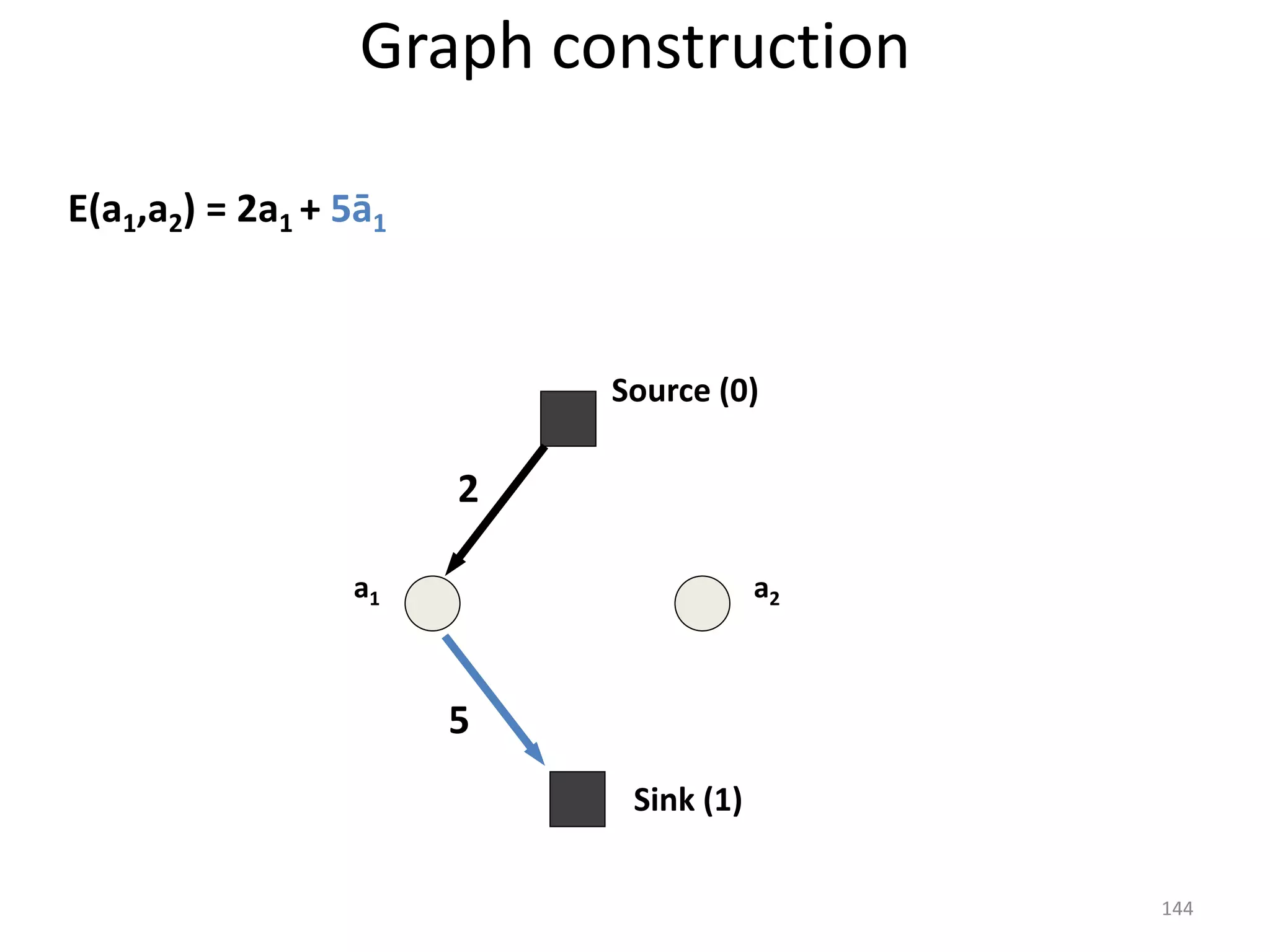
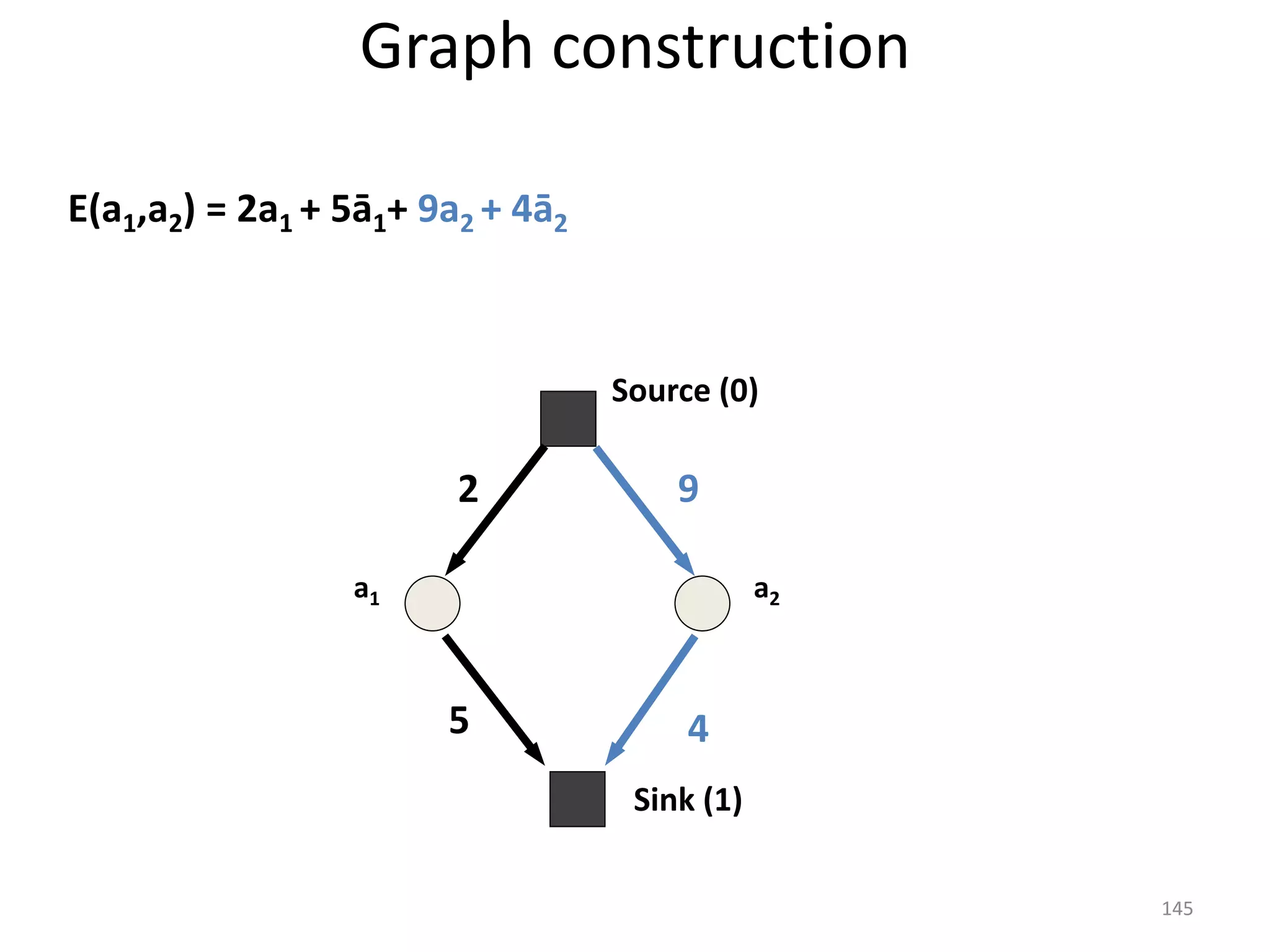
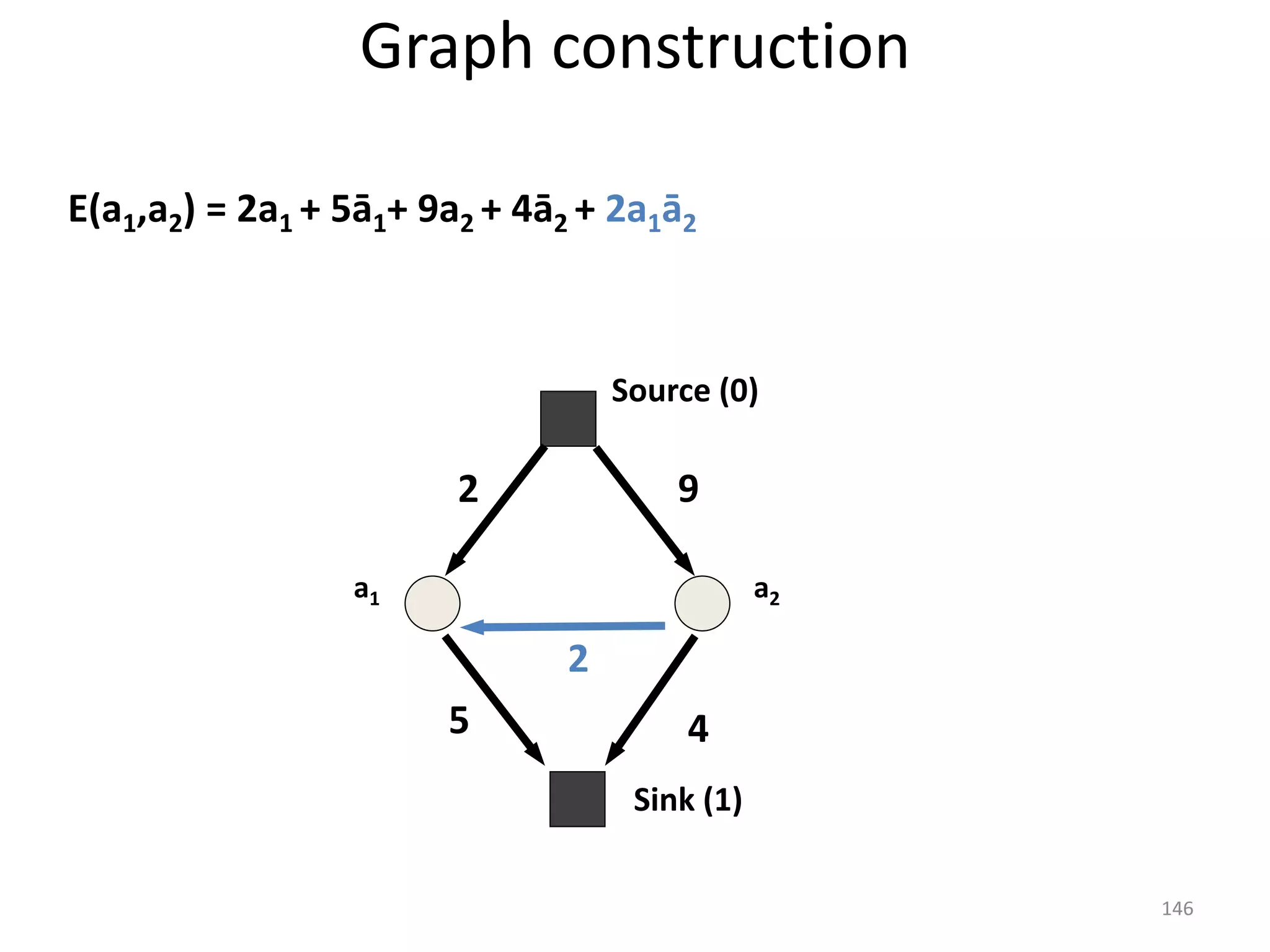
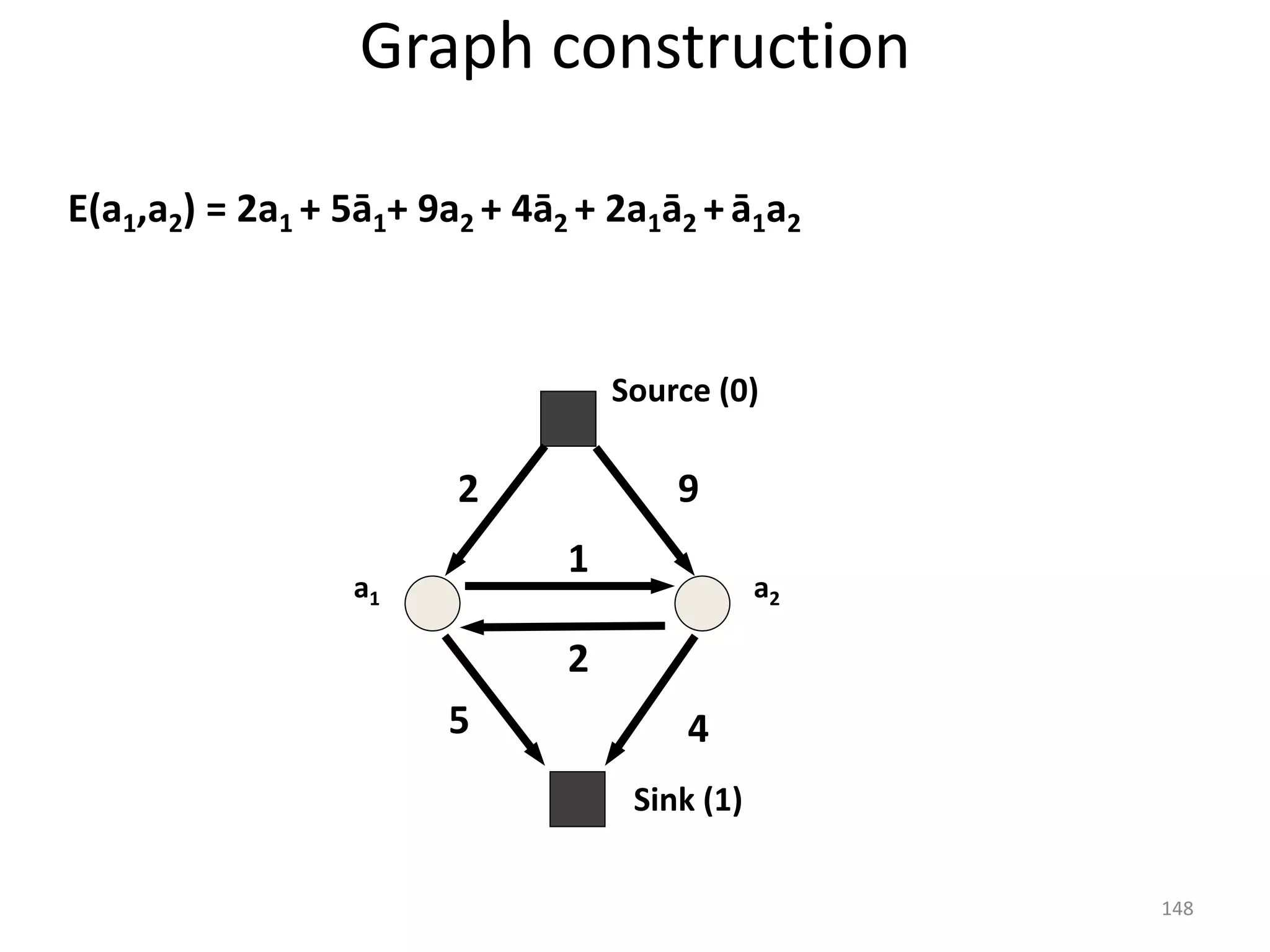
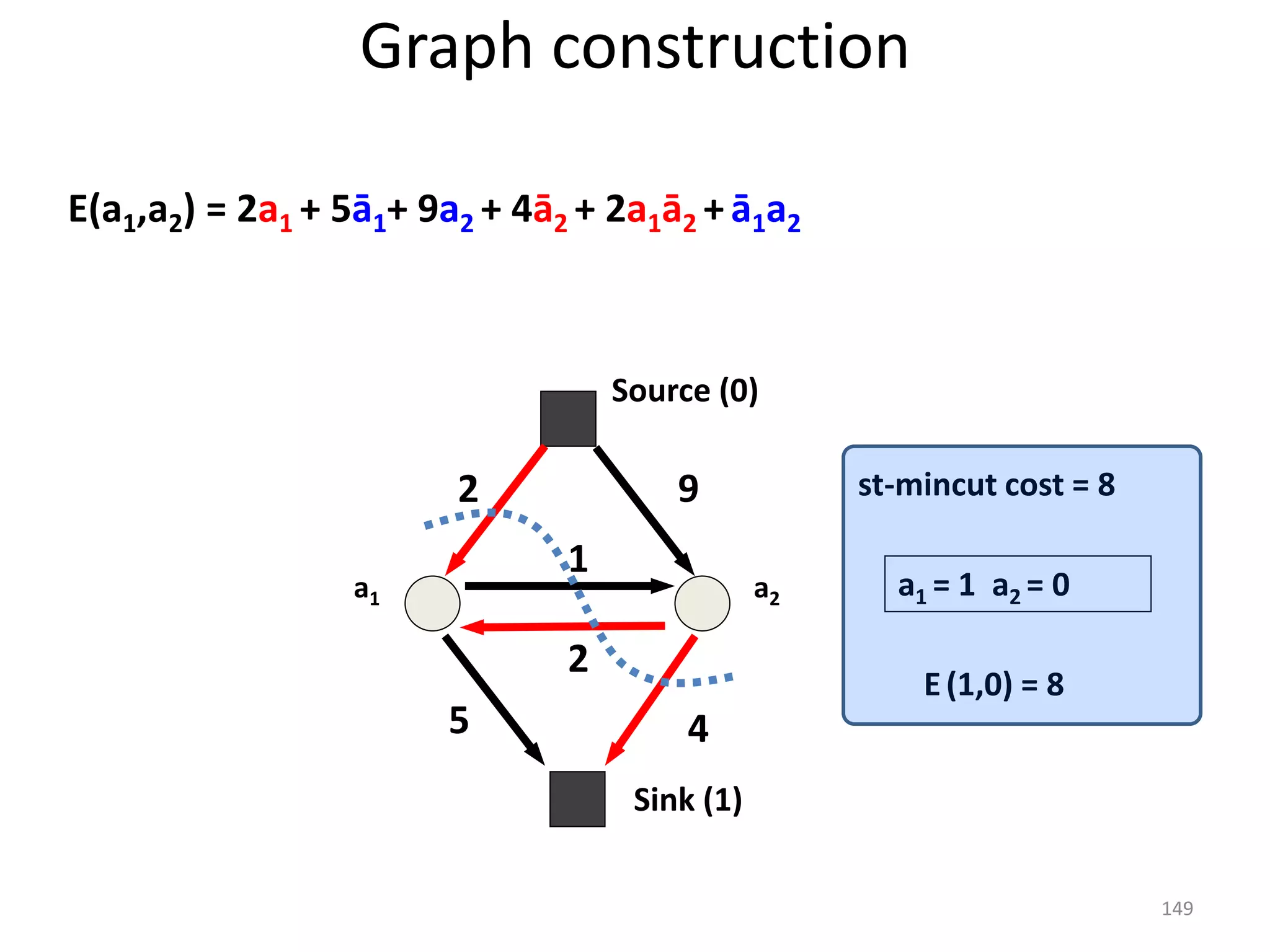
The document discusses maximum flow algorithms. It begins by introducing concepts such as functions on arcs, excess functions, s-t flows, s-t cuts, and the relationship between flows and cuts. Specifically, it notes that the value of a flow will always be less than or equal to the capacity of a cut, with equality holding when the flow saturates the outgoing arcs of the cut and sends no flow along the incoming arcs. The document then outlines an algorithmic approach of finding s-t paths in the residual graph and pushing flow along these paths until no more exist. However, it notes this will not necessarily find the true maximum flow.

1. Discrete Optimization
Lecture 2
Part 2
Maximum Flow Algorithms
Mahdi Abbasi, Associate Professor
Department of Computer Engineering, Bu Ali Sina University
Email: abbasi@basu.ac.ir
Reference of this lecture slides:
1. Ahuja, Ravindra K., Thomas L. Magnanti, and James B.
Orlin. Network Flows: Theory, Algorithms, and Applications. Upper
Saddle River, NJ: Prentice Hall, 1993. ISBN: 9780136175490.
(Chaps. 6,7) 1

2. • Preliminaries
– Functions and Excess Functions
– s-t Flow
– s-t Cut
– Flows vs. Cuts
• Maximum Flow
• Algorithms
Outline
2

3. Functions on Arcs
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
D = (V, A)
Arc capacities c(a)
Function f: A  Reals
3 2
1 10
3
Excess function Ef(v)
Incoming value
-
Outgoing value
4
3

4. Functions on Arcs
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
D = (V, A)
Arc capacities c(a)
Function f: A  Reals
3 2
1 10
3
Excess function Ef(v)
Σain-arcs(v) f(a)
-
Outgoing value
4
4

5. Functions on Arcs
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
Function f: A  Reals
3 2
1 10
3
Excess function Ef(v)
4
D = (V, A)
Arc capacities c(a)
Σain-arcs(v) f(a)
-
Σaout-arcs(v) f(a)
5

6. Functions on Arcs
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
Function f: A  Reals
3 2
1 10
3
Excess function Ef(v)
f(in-arcs(v))
-
f(out-arcs(v))
Ef(v1) -6
4
D = (V, A)
Arc capacities c(a)
6

7. Functions on Arcs
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
Function f: A  Reals
3 2
1 10
3
Excess function Ef(v)
Ef(v2) 14
f(in-arcs(v))
-
f(out-arcs(v))
4
D = (V, A)
Arc capacities c(a)
7

8. Excess Functions of Vertex Subsets
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
3 2
1 10
3
Excess function Ef(U)
Incoming Value
-
Outgoing Value
4
8

9. Excess Functions of Vertex Subsets
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
3 2
1 10
3
Excess function Ef(U)
Σain-arcs(U) f(a)
-
Outgoing Value
4
9

10. Excess Functions of Vertex Subsets
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
3 2
1 10
3
Excess function Ef(U)
Σain-arcs(U) f(a)
-
Σaout-arcs(U) f(a)
4
10

11. Excess Functions of Vertex Subsets
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
3 2
1 10
3
Excess function Ef(U)
f(in-arcs(U))
-
f(out-arcs(U))
Ef({v1,v2})
4
8
11

12. Excess Functions of Vertex Subsets
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
3 2
1 10
3
Excess function Ef(U)
f(in-arcs(U))
-
f(out-arcs(U))
Ef(U) = ΣvU Ef(v)
Ef({v1,v2})
4
-6 + 14
12

13. • Preliminaries
– Functions and Excess Functions
– s-t Flow
– s-t Cut
– Flows vs. Cuts
• Maximum Flow
• Algorithms
Outline
13

14. s-t Flow
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
Function flow: A  R
Flow of arc ≤ arc capacity
Flow is non-negative
For all vertex expect s,t
Incoming flow
= Outgoing flow
14

15. s-t Flow
Function flow: A  R
flow(a) ≤ c(a)
Flow is non-negative
For all vertex expect s,t
Incoming flow
= Outgoing flow
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
15

16. s-t Flow
Function flow: A  R
flow(a) ≤ c(a)
For all vertex expect s,t
Incoming flow
= Outgoing flow
flow(a) ≥ 0
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
16

17. s-t Flow
Function flow: A  R
flow(a) ≤ c(a)
flow(a) ≥ 0
For all v  V {s,t}
Incoming flow
= Outgoing flow
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
17

18. s-t Flow
Function flow: A  R
flow(a) ≤ c(a)
flow(a) ≥ 0
For all v  V {s,t}
= Outgoing flow
Σ(u,v)A flow((u,v))
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
18

19. s-t Flow
Function flow: A  R
flow(a) ≤ c(a)
flow(a) ≥ 0
For all v  V {s,t}
= Σ(v,u)A flow((v,u))
Σ(u,v)A flow((u,v))
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
19

20. s-t Flow
Function flow: A  R
flow(a) ≤ c(a)
flow(a) ≥ 0
For all v  V {s,t}
Eflow(v) = 0
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
20

21. s-t Flow
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
Function flow: A  R
flow(a) ≤ c(a)
flow(a) ≥ 0
For all v  V {s,t}
Eflow(v) = 0
3
1 10
3
4
✗ 21

22. s-t Flow
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
Function flow: A  R
flow(a) ≤ c(a)
flow(a) ≥ 0
For all v  V {s,t}
Eflow(v) = 0
-1
-1
-1
✗ 22

23. s-t Flow
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
Function flow: A  R
flow(a) ≤ c(a)
flow(a) ≥ 0
For all v  V {s,t}
Eflow(v) = 0
1
1
1
✓ 23

24. Value of s-t Flow
Outgoing flow of s
- Incoming flow of s
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
24

25. Value of s-t Flow
Σ(s,v)A flow((s,v))
- Σ(u,s)A flow((u,s))
-Eflow(s) Eflow(t)
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
25

26. Value of s-t Flow
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
Σ(s,v)A flow((s,v))
- Σ(u,s)A flow((u,s))
-Eflow(s) Eflow(t)
1
1
1
Value = 1
26

27. • Preliminaries
– Functions and Excess Functions
– s-t Flow
– s-t Cut
– Flows vs. Cuts
• Maximum Flow
• Algorithms
Outline
27

28. Cut
v1 v2
v3 v4
10
5
3 2
Let U be a subset of V
C is a set of arcs such that
• (u,v)  A
• u  U
• v  VU
D = (V, A)
C is a cut in the digraph D 28

29. Cut
v1 v2
v3 v4
What is C?
D = (V, A)
U
VU
{(v1,v2),(v1,v4)} ?
{(v1,v4),(v3,v2)} ?
{(v1,v4)} ?
✓
10
5
3 2
29

30. Cut
v1 v2
v3 v4
What is C?
D = (V, A)
U
VU
{(v1,v2),(v1,v4),(v3,v2)} ?
{(v1,v4),(v3,v2)} ?
{(v4,v3)} ?
✓
10
5
3 2
30

31. Cut
What is C?
D = (V, A)
VU
U
{(v1,v2),(v1,v4),(v3,v2)} ?
{(v1,v4),(v3,v2)} ?
{(v3,v2)} ?
✓
v1 v2
v3 v4
10
5
3 2
31

32. Cut
C = out-arcs(U)
D = (V, A)
v1 v2
v3 v4
10
5
3 2
32

33. Capacity of Cut
Sum of capacity of all
arcs in C
v1 v2
v3 v4
10
5
3 2
33

34. Capacity of Cut
Σa  C c(a)
v1 v2
v3 v4
10
5
3 2
34

35. Capacity of Cut
3
v1 v2
v3 v4
U
VU
10
5
3 2
35

36. Capacity of Cut
15
VU
U
v1 v2
v3 v4
10
5
3 2
36

37. s-t Cut
A source vertex “s”
C is a cut such that
• s  U
• t  VU
D = (V, A)
C is an s-t cut
A sink vertex “t”
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
37

38. Capacity of s-t Cut
Σa  C c(a)
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
38

39. Capacity of s-t Cut
5
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
39

40. Capacity of s-t Cut
17
v1 v2
v3 v4
6
5
3
s
t
1 8
7 3
2
40

41. • Preliminaries
– Functions and Excess Functions
– s-t Flow
– s-t Cut
– Flows vs. Cuts
• Maximum Flow
• Algorithms
Outline
41

42. Flows vs. Cuts
An s-t flow function flow: A  Reals
An s-t cut C such that s  U, t  VU
Value of flow ≤ Capacity of C
42

43. Flows vs. Cuts
Value of flow
= -Eflow(s) - ΣvU{s} Eflow(v)
= -Eflow(s)
= -Eflow(U)
= flow(out-arcs(U))
- flow(in-arcs(U))
≤ Capacity of C
- flow(in-arcs(U))
43

44. Flows vs. Cuts
Value of flow
= -Eflow(s) - ΣvU{s} Eflow(v)
= -Eflow(s)
= -Eflow(U)
= flow(out-arcs(U))
- flow(in-arcs(U))
≤ Capacity of C
When does equality hold? 44

45. Flows vs. Cuts
Value of flow
= -Eflow(s) - ΣvU{s} Eflow(v)
= -Eflow(s)
= -Eflow(U)
= flow(out-arcs(U))
- flow(in-arcs(U))
≤ Capacity of C
flow(a) = c(a), a  out-arcs(U) flow(a) = 0, a  in-arcs(U)45

46. Flows vs. Cuts
Value of flow
= -Eflow(s) - ΣvU{s} Eflow(v)
= -Eflow(s)
= -Eflow(U)
= flow(out-arcs(U))
- flow(in-arcs(U))
= Capacity of C
flow(a) = c(a), a  out-arcs(U) flow(a) = 0, a  in-arcs(U)46

47. • Preliminaries
• Maximum Flow
– Residual Graph
– Max-Flow Min-Cut Theorem
• Algorithms
Outline
47

48. Maximum Flow Problem
Find the flow with the
maximum value !!
Σ(s,v)A flow((s,v))
- Σ(u,s)A flow((u,s))
v1 v2
3
s
t
2 4
1 2
One suggestion to solve this problem !! 48

49. Passing Flow through s-t Paths
Find an s-t path where
flow(a) < c(a) for all arcs
v1 v2
3
s
t
2 4
1 2
49

50. Passing Flow through s-t Paths
Find an s-t path where
flow(a) < c(a) for all arcs
v1 v2
3
s
t
2 4
1 2
Pass maximum allowable
flow through the arcs
1
1
50

51. Passing Flow through s-t Paths
Find an s-t path where
flow(a) < c(a) for all arcs
v1 v2
3
s
t
2 4
1 2
1
1
51

52. Passing Flow through s-t Paths
Find an s-t path where
flow(a) < c(a) for all arcs
v1 v2
3
s
t
2 4
1 2
1
1
Pass maximum allowable
flow through the arcs
2
2
52

53. Passing Flow through s-t Paths
Find an s-t path where
flow(a) < c(a) for all arcs
v1 v2
3
s
t
2 4
1 2
1
1
No more paths.
2
2
Stop.
Will this give us maximum flow? NO !!! 53

54. Passing Flow through s-t Paths
Find an s-t path where
flow(a) < c(a) for all arcs
v1 v2
3
s
t
2 4
1 2
Pass maximum allowable
flow through the arcs
2
2
2
54

55. Passing Flow through s-t Paths
Find an s-t path where
flow(a) < c(a) for all arcs
v1 v2
3
s
t
2 4
1 2
2
2
2
No more paths. Stop.
Incorrect Answer !!
Another method?
55

56. • Preliminaries
• Maximum Flow
– Residual Graph
– Max-Flow Min-Cut Theorem
• Algorithms
Outline
56

57. Residual Graph
v1 v2
3
s
t
2 4
1 2
2
2
2
v1 v2
s
t
Arcs where flow(a) < c(a) 57

58. Residual Graph
v1 v2
3
s
t
2 4
1 2
2
2
2
v1 v2
s
t
Inverse of arcs where flow(a) > 0
Including arcs to s and from t is not necessary
58

59. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
Start with zero flow.
v1 v2
s
t
59

60. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
Find an s-t path in the residual graph.
v1 v2
s
t
60

61. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
Find an s-t path in the residual graph.
v1 v2
s
t
61

62. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
For inverse arcs in path, subtract flow K.
v1 v2
s
t
62

63. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
For forward arcs in path, add flow K.
v1 v2
s
t
Choose maximum allowable value of K.
63

64. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
For forward arcs in path, add flow K.
v1 v2
s
t
Choose maximum allowable value of K.
2
2
2
64

65. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
Update the residual graph.
2
2
2
v1 v2
s
t
65

66. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
2
2
2
v1 v2
s
t
Find an s-t path in the residual graph. 66

67. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
2
2
2
v1 v2
s
t
Find an s-t path in the residual graph. 67

68. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
2
2
2
v1 v2
s
t
Add K to (s,v2) and (v1,t). Subtract K from (v1,v2).
Choose maximum allowable value of K.
68

69. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
2
1
2
v1 v2
s
t
Add K to (s,v2) and (v1,t). Subtract K from (v1,v2).
Choose maximum allowable value of K.
1
1
69

70. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
2
1
2
v1 v2
s
t
1
1
Update the residual graph. 70

71. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
2
1
2
v1 v2
s
t
1
1
Find an s-t path in the residual graph. 71

72. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
2
1
2
v1 v2
s
t
1
1
No more s-t paths. Stop. 72

73. Maximum Flow using Residual Graphs
v1 v2
3
s
t
2 4
1 2
2
1
2
v1 v2
s
t
1
1
Correct Answer. 73

74. Maximum Flow using Residual Graphs
v1 v2
3
s
t
1 4
2 2
Start with zero flow
v1 v2
s
t
74

75. Maximum Flow using Residual Graphs
v1 v2
3
s
t
1 4
2 2
Find an s-t path in the residual graph.
v1 v2
s
t
75

76. Maximum Flow using Residual Graphs
v1 v2
3
s
t
1 4
2 2
Find an s-t path in the residual graph.
v1 v2
s
t
76

77. Maximum Flow using Residual Graphs
v1 v2
3
s
t
1 4
2 2
For inverse arcs in path, subtract flow K.
v1 v2
s
t
77

78. Maximum Flow using Residual Graphs
v1 v2
3
s
t
1 4
2 2
For forward arcs in path, add flow K.
v1 v2
s
t
Choose maximum allowable value of K.
78

79. Maximum Flow using Residual Graphs
v1 v2
3
s
t
1 4
2 2
For forward arcs in path, add flow K.
v1 v2
s
t
Choose maximum allowable value of K.
1
1
1
79

80. Maximum Flow using Residual Graphs
v1 v2
3
s
t
1 4
2 2
Update the residual graph.
1
1
1
v1 v2
s
t
80

81. Maximum Flow using Residual Graphs
v1 v2
3
s
t
1 4
2 2
1
1
1
v1 v2
s
t
Find an s-t path in the residual graph. 81

82. Maximum Flow using Residual Graphs
v1 v2
s
t
Find an s-t path in the residual graph.
v1 v2
3
s
t
1 4
2 2
1
1
1
82

83. Maximum Flow using Residual Graphs
v1 v2
s
t
Add K to (s,v2) and (v1,t). Subtract K from (v1,v2).
Choose maximum allowable value of K.
v1 v2
3
s
t
1 4
2 2
1
1
1
83

84. Maximum Flow using Residual Graphs
v1 v2
3
s
t
1 4
2 2
1
1
v1 v2
s
t
Add K to (s,v2) and (v1,t). Subtract K from (v1,v2).
Choose maximum allowable value of K.
1
1
84

85. Maximum Flow using Residual Graphs
v1 v2
s
t
Update the residual graph.
v1 v2
3
s
t
1 4
2 2
1
1
1
1
85

86. Maximum Flow using Residual Graphs
Find an s-t path in the residual graph.
v1 v2
s
t
v1 v2
3
s
t
1 4
2 2
1
1
1
1
86

87. Maximum Flow using Residual Graphs
Find an s-t path in the residual graph.
v1 v2
s
t
v1 v2
3
s
t
1 4
2 2
1
1
1
1
87

88. Maximum Flow using Residual Graphs
v1 v2
s
t
Add K to (s,v2) and (v2,t).
Choose maximum allowable value of K.
v1 v2
3
s
t
1 4
2 2
1
1
1
1
88

89. Maximum Flow using Residual Graphs
v1 v2
s
t
Add K to (s,v2) and (v2,t).
Choose maximum allowable value of K.
v1 v2
3
s
t
1 4
2 2
1
2
2
1
89

90. Maximum Flow using Residual Graphs
v1 v2
s
t
Update residual graph.
v1 v2
3
s
t
1 4
2 2
1
2
2
1
90

91. Maximum Flow using Residual Graphs
No more s-t paths. Stop.
v1 v2
s
t
v1 v2
3
s
t
1 4
2 2
1
2
2
1
91

92. Maximum Flow using Residual Graphs
How can I be sure this will always work?
v1 v2
s
t
v1 v2
3
s
t
1 4
2 2
1
2
2
1
92

93. • Preliminaries
• Maximum Flow
– Residual Graph
– Max-Flow Min-Cut Theorem
• Algorithms
Outline
93

94. Max-Flow Min-Cut
Let the subset of vertices U be reachable from s.
t is not in U.
v1 v2
s
t
v1 v2
3
s
t
1 4
2 2
1
2
2
1
94

95. Max-Flow Min-Cut
For all a  out-arcs(U), flow(a) = c(a).
Or else a will be in the residual graph.
v1 v2
s
t
v1 v2
3
s
t
1 4
2 2
1
2
2
1
95

96. Max-Flow Min-Cut
For all a  in-arcs(U), flow(a) = 0.
Or else inverse of a will be in the residual graph.
v1 v2
s
t
v1 v2
3
s
t
1 4
2 2
1
2
2
1
96

97. Max-Flow Min-Cut
For all a  in-arcs(U), flow(a) = 0.
For all a  out-arcs(U), flow(a) = c(a).
v1 v2
s
t
v1 v2
3
s
t
1 4
2 2
1
2
2
1
97

98. Flows vs. Cuts
Value of flow
= -Eflow(s) - ΣvU{s} Eflow(v)
= -Eflow(s)
= -Eflow(U)
= flow(out-arcs(U))
- flow(in-arcs(U))
= Capacity of C
flow(a) = c(a), a  out-arcs(U) flow(a) = 0, a  in-arcs(U)98

99. Max-Flow Min-Cut
Capacity(C) = Value(flow)
Minimum Cut Maximum Flow
v1 v2
s
t
v1 v2
3
s
t
1 4
2 2
1
2
2
1
99

100. • Preliminaries
• Maximum Flow
• Algorithms
– Ford-Fulkerson Algorithm
– Dinits Algorithm
Outline
100

101. Ford-Fulkerson Algorithm
Start with flow = 0 for all arcs.
Find an s-t path in the residual graph.
Pass maximum allowable flow.
Subtract from inverse arcs.
Add to forward arcs.
REPEAT
Until s and t are disjoint in the residual graph. 101

102. Ford-Fulkerson Algorithm
v1 v2
1
s
t
10k
Start with zero flow
v1 v2
s
t
10k
10k 10k
102

103. Ford-Fulkerson Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
Find an s-t path in the residual graph. 103

104. Ford-Fulkerson Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
Find an s-t path in the residual graph. 104

105. Ford-Fulkerson Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
Pass the maximum allowable flow. 105

106. Ford-Fulkerson Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
Pass the maximum allowable flow.
1
1
1
106

107. Ford-Fulkerson Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
Update the residual graph.
1
1
1
107

108. Ford-Fulkerson Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
1
1
1
Find an s-t path in the residual graph. 108

109. Ford-Fulkerson Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
1
1
1
Find an s-t path in the residual graph. 109

110. Ford-Fulkerson Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
1
1
1
Complexity is exponential in k. 110

111. Ford-Fulkerson Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
1
1
1
Irrational arc lengths can lead to infinite iterations.
For examples, see Uri Zwick, 1993
111

112. Ford-Fulkerson Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
1
1
1
There are good paths and bad paths.
Choose wisely.
112

113. • Preliminaries
• Maximum Flow
• Algorithms
– Ford-Fulkerson Algorithm
– Dinits Algorithm (Simple Version)
Outline
113

114. Dinits Algorithm
Start with flow = 0 for all arcs.
Find the minimum s-t path
in the residual graph.
Pass maximum allowable flow.
Subtract from inverse arcs.
Add to forward arcs.
REPEAT
Until s and t are disjoint in the residual graph. 114

115. Dinits Algorithm
v1 v2
1
s
t
10k
Start with zero flow
v1 v2
s
t
10k
10k 10k
115

116. Dinits Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
Find the minimum s-t path in the residual graph.
116

117. Dinits Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
Find the minimum s-t path in the residual graph.
117

118. Dinits Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
Pass the maximum allowable flow. 118

119. Dinits Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
Pass the maximum allowable flow.
10k
10k
119

120. Dinits Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
Update the residual graph.
10k
10k
120

121. Dinits Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
10k
10k
Find the minimum s-t path in the residual graph.
121

122. Dinits Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
10k
10k
Find the minimum s-t path in the residual graph.
122

123. Dinits Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
10k
10k
Pass the maximum allowable flow. 123

124. Dinits Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
10k
10k
Pass the maximum allowable flow.
10k
10k
124

125. Dinits Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
10k
10k
Update the residual graph.
10k
10k
125

126. Dinits Algorithm
v1 v2
1
s
t
10k
v1 v2
s
t
10k
10k 10k
10k
10k
No more s-t paths. Stop.
10k
10k
126

127. Computational Complexity
Strongly polynomial: O(m2n) m = |A|, n = |V|
Finding shortest s-t path O(m)
Number of iterations O(mn)
Proof?
First, a Lemma.
127

128. Lemma
μ(D) = length of shortest path for D
v1 v2
s
t
v3
μ(D) = 3
128

129. Lemma
v1 v2
s
t
v3
α(D) = arcs present in at least one shortest path 129

130. Lemma
v1 v2
s
t
v3
α(D) = arcs present in at least one shortest path 130

131. Lemma
v1 v2
s
t
v3
S(D) = (V, A “union” inverse arcs of α(D))
v1 v2
s
t
v3
Including arcs to s and from t is not necessary
131

132. Lemma
v1 v2
s
t
v3
v1 v2
s
t
v3
μ(D) = μ(S(D)) α(D) = α(S(D))
Proof left as exercise !!!
132

133. Computational Complexity
Strongly polynomial: O(m2n) m = |A|, n = |V|
Finding shortest s-t path O(m)
Number of iterations O(mn)
133

134. Computational Complexity
Current residual graph D0
Find a shortest path P in D0
New residual graph D1
D1 is a subgraph of S(D0)
μ(D1) ≥ μ(S(D0)) = μ(D0)
134

135. Computational Complexity
μ(D1) ≥ μ(S(D0)) = μ(D0) Assume Equality
At least one arc a in P, a  α(D0) and a  α(D1)
Specifically, an arc that is saturated in path P
α(D1) α(S(D0)) = α(D0)
“subset of” 135

136. Computational Complexity
μ(D1) ≥ μ(S(D0)) = μ(D0) Assume Equality
At least one arc a in P, a  α(D0) and a  α(D1)
Specifically, an arc that is saturated in path P
α(D1) α(S(D0)) = α(D0)
“strict subset of” 136

137. Computational Complexity
Therefore, total iterations = O(mn)
At each iteration, either μ increases
Or size of α decreases
Overall complexity = O(m2n)
137

138. Let us take an example
Image segmentation
Image Segmentation
Following slides are based on P. Kohli’s tutorial
138

139. Let us take an example
Image segmentation
Image Construct a graph
T
S
139

140. So how does it work?
Image segmentation
Set the edge weights
T
S
140

141. Construct a graph such that:
1.Any st-cut corresponds to an assignment of x
2.The cost of the cut is equal to the energy of x : E(x)
Solution
T
S st-mincut
E(x)
How does it work?
141

142. Sink (1)
Source (0)
a1 a2
E(a1,a2)
Graph construction
142

143. Sink (1)
Source (0)
a1 a2
E(a1,a2) = 2a1
2
Graph construction
143

144. a1 a2
E(a1,a2) = 2a1 + 5ā1
2
5
Sink (1)
Source (0)
Graph construction
144

145. a1 a2
E(a1,a2) = 2a1 + 5ā1+ 9a2 + 4ā2
2
5
9
4
Sink (1)
Source (0)
Graph construction
145

146. a1 a2
E(a1,a2) = 2a1 + 5ā1+ 9a2 + 4ā2 + 2a1ā2
2
5
9
4
2
Sink (1)
Source (0)
Graph construction
146

147. a1 a2
E(a1,a2) = 2a1 + 5ā1+ 9a2 + 4ā2 + 2a1ā2 + ā1a2
2
5
9
4
2
1
Sink (1)
Source (0)
Graph construction
147

148. a1 a2
E(a1,a2) = 2a1 + 5ā1+ 9a2 + 4ā2 + 2a1ā2 + ā1a2
2
5
9
4
2
1
Sink (1)
Source (0)
Graph construction
148

149. a1 a2
E(a1,a2) = 2a1 + 5ā1+ 9a2 + 4ā2 + 2a1ā2 + ā1a2
2
5
9
4
2
1
Sink (1)
Source (0)
a1 = 1 a2 = 0
E(1,0) = 8
st-mincut cost = 8
Graph construction
149