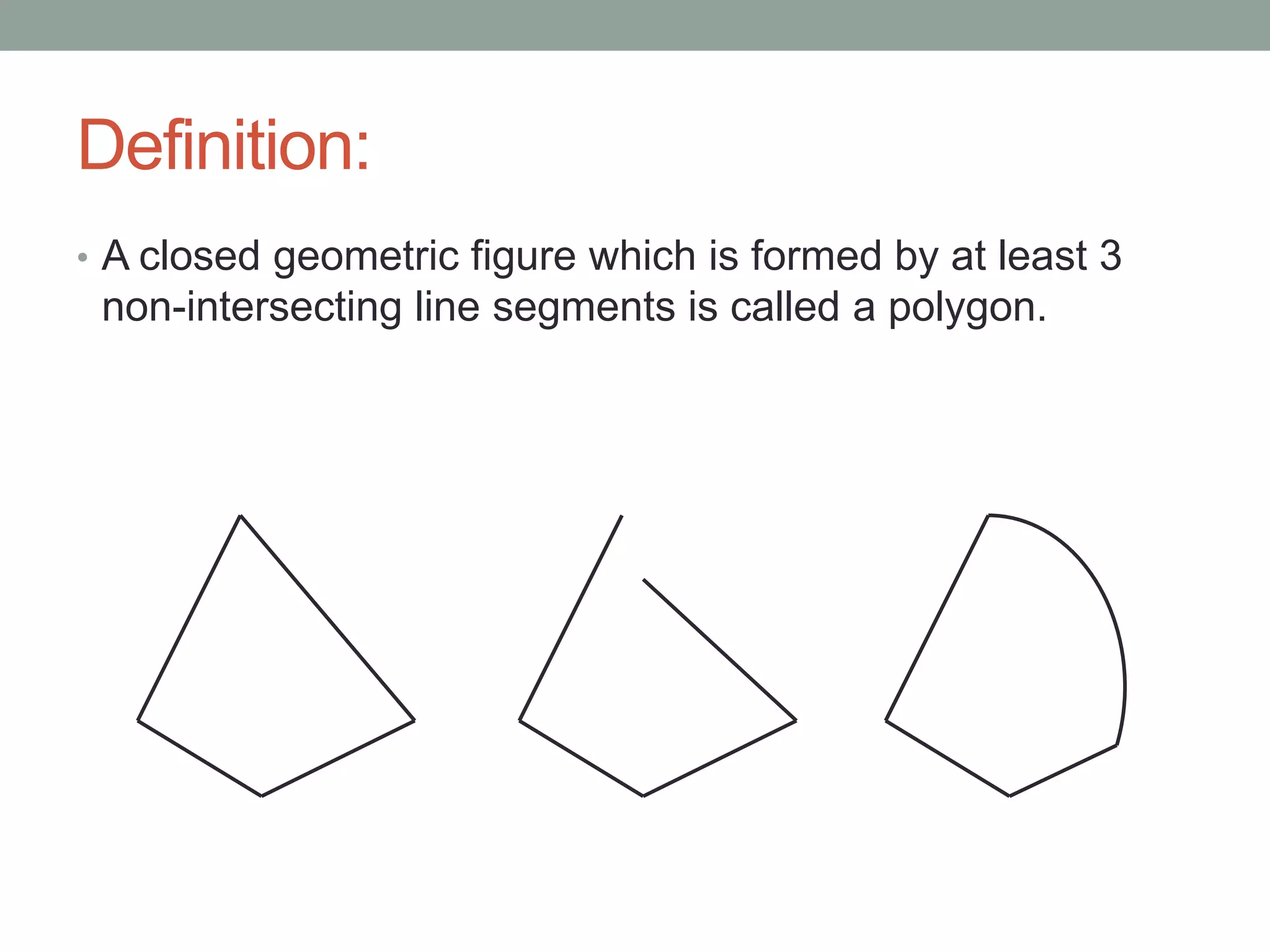
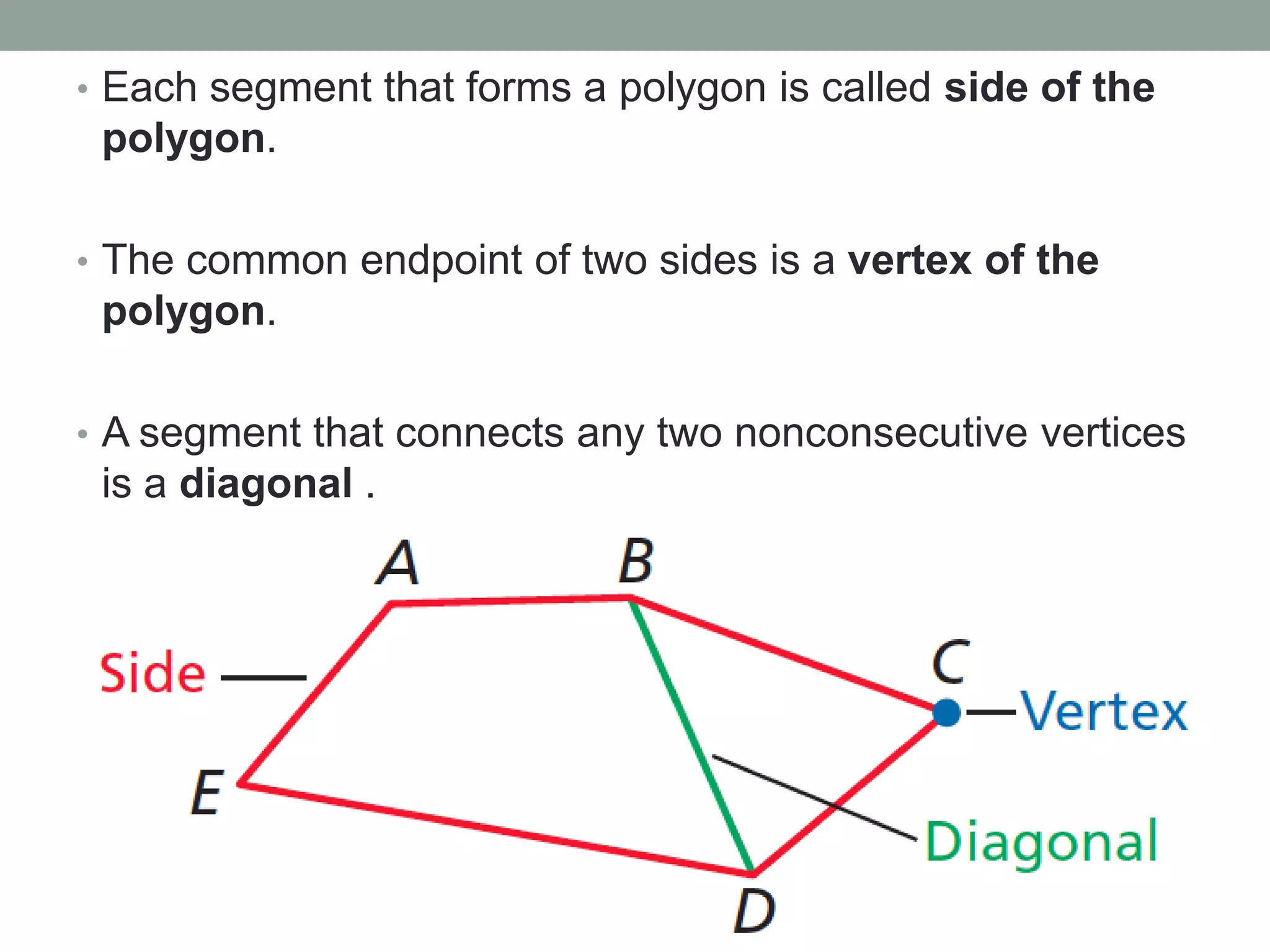
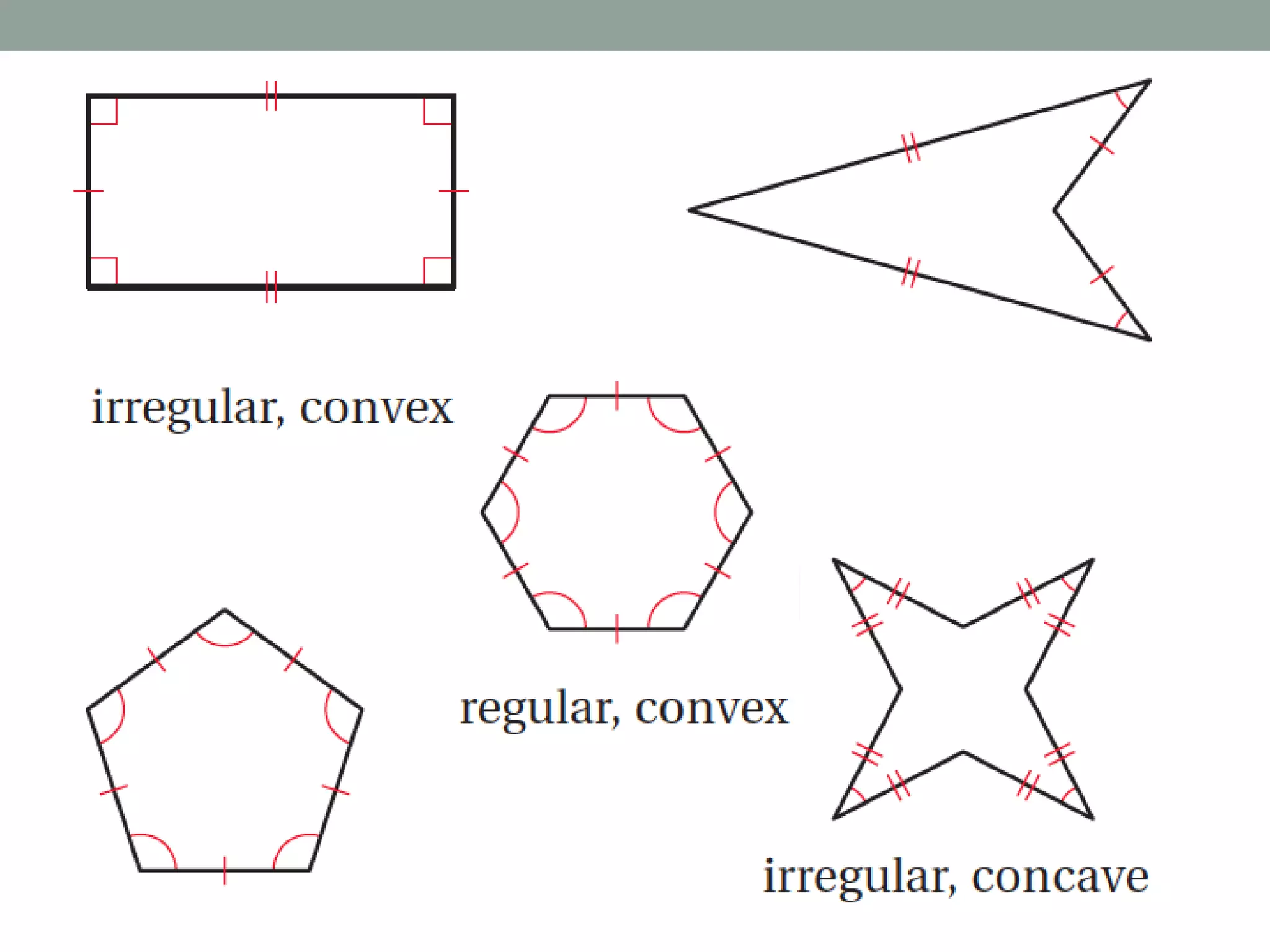
This document defines key properties and attributes of polygons. It explains that a polygon is a closed figure formed by at least 3 non-intersecting line segments, with sides connecting vertices. A regular polygon is both equilateral and equiangular, while an irregular polygon is not. The interior angles of a convex polygon sum to (n-2)180 degrees, and the exterior angles sum to 360 degrees. Examples are provided to illustrate how to use these properties to calculate angle measures.

1. PROPERTIES AND ATTRIBUTES OF
POLYGONS

2. Definition:
• A closed geometric figure which is formed by at least 3
non-intersecting line segments is called a polygon.

3. • Each segment that forms a polygon is called side of the
polygon.
• The common endpoint of two sides is a vertex of the
polygon.
• A segment that connects any two nonconsecutive vertices
is a diagonal .

4. • You can name a
polygon by the
number of its sides.

5. • A regular polygon is one that is both equilateral and
equiangular. If a polygon is not regular, it is called
irregular.
• A polygon is concave if any part of a diagonal contains
points in the exterior of the polygon.
• If no diagonal contains points in the exterior, then the
polygon is convex .
• A regular polygon is always convex.

7. Polygon Angle Sum Theorem
• The sum of the interior angle measures of a convex
polygon with n sides is (n - 2) 180°.

8. Examples:
• Find the sum of the interior angle measures of a convex
octagon.
• Find the measure of each interior angle of a regular
nonagon.
• Find the measure of each interior angle of quadrilateral
with angles of x˚, 2x˚, 3x˚ and 4x˚.

9. Polygon Exterior Angle Sum Theorem
• The sum of the exterior angle measures, one angle at
each vertex, of a convex polygon is 360°.
• The measure of each exterior angle of a regular polygon
with n sides is 360˚/n

10. Examples:
• Find the measure of each exterior angle of a regular
hexagon.
• Find the measure of each exterior angle of a regular
heptagon.