Ανδρέας Λύκος | μαθηματικός, συγγραφέας- «Πόσο φράκταλ είναι ο Pollock;» Μπορούσε, άραγε, ο καλλιτέχνης να ελέγξει τη ροή του χρώματος στον καμβά; Μήπως η ψυχοσύνθεση του Πόλοκ ήταν αυτή που τον οδήγησε να παράγει πίνακες με τη συγκεκριμένη χαρακτηριστική δομή;

1. Ανδρέας Λύκος
( ) -
Μαθηματικός Πειραματικό ΓΕΛ Κομοτηνής MSc -
Στατιστικής Συγγραφέας
Πόσο φράκταλ είναι ο
Pollock;
Βόλος
π
Πανε ιστήμιο
(28
Θεσσαλίας ης
78
Οκτωβρίου )
6
Σάββατο
Ιουλίου
18:30-19:30 &19:45-20:45

2. o Εισαγωγή στις βασικές έννοιες
o :
Διερεύνηση Εμφανίζεται φράκταλ δομή στα έργα του
;
Πόλοκ
o :
Εφαρμογή π
Αξιο οιώντας τη μέθοδο Box Counting
μετράμε τη διάσταση φράκταλ μιας ακτογραμμής!
o Προτάσεις π π
για εφαρμογή των αρα άνω στη σχολική
-
τάξη Σύνδεση με τα ΠΜΑ

3. • ( ):
Φράκταλ μορφόκλασμα ή μορφοκλασματικό σύνολο
π π
ένα γεωμετρικό σχήμα ου ε αναλαμβάνεται αυτούσιο
π .
σε ά ειρο βαθμό μεγέθυνσης
• π π
Όσες φορές και να μεγεθυνθεί ο οιοδή οτε τμήμα ενός
π
φράκταλ θα συνεχίζει να αρουσιάζει ένα εξίσου
π π
ερί λοκο σχέδιο με π
μερική ή ολική ε ανάληψη του
αρχικού.
• π
Χαρακτηριστικό ε ομένως των φράκταλ είναι η -
αυτό
ομοιότητα (self-similarity) π , π
σε κά οιες δομές τους η ο οία
π π .
εμφανίζεται σε διαφορετικά ε ί εδα μεγέθυνσης
ΜΙΑ ΣΥΝΤΟΜΗ ΓΝΩΡΙΜΙΑ… FRACTAL

5. π π
Πώς μετράω τον βαθμό ολυ λοκότητας ενός
;
φράκταλ
𝐷𝐻 =
𝑙𝑜𝑔 4
𝑙𝑜𝑔 3
≅1.2619
Felix Hausdorff

7. ΜΙΑ ΣΥΝΤΟΜΗ ΓΝΩΡΙΜΙΑ… POLLOCK
• π π
Τα ρώτα έργα του Πόλοκ είναι ε ηρεασμένα
π
α ό τους Μεξικανούς ζωγράφους Σικέιρος
.
και Ριβέρα
• π 1938 – 1944
Τα έργα της εριόδου είναι
π π
ε ηρεασμένα α ό τις ψυχολογικές θεωρίες
.
του Καρλ Γκούσταβ Γιουνγκ
• π : 1944
Δημιουργικότερη ερίοδός του μετά το
π
ε ινοεί την τεχνική του dripping.
• π π
Βασικός εκ ρόσω ος του αφηρημένου
π .
εξ ρεσιονισμού
• 1956
Σκοτώνεται το σε αυτοκινητιστικό
(π
δυστύχημα ιθανότατα οδηγούσε
Paul Jackson Pollock (1912 – 1956)

8. Pollock
dripping
technique
1945
the road
to…

9. “I DON’T PAINT NATURE, I AM NATURE”

10. 1 2
3
4 6
5

11. Πόσο φράκταλ είναι ο Pollock;
Δομή VS Χάος ή Δομή στο
;
Χάος
Number 32, 1950

12. Μέθοδος Box Counting

13. Blue Poles: Number 11, 1952 (210.4 cm · 486.8 cm)

14. Μέθοδος Box Counting
Blue Poles: Number 11, 1952 (210.4 cm · 486.8 cm)

15. Μέθοδος Box Counting
Blue Poles: Number 11, 1952 (210.4 cm · 486.8 cm)
Box Counting Analysis : π -
ανά χρώμα μ λε μαύρο, αλουμίνιο, γκρι,
ανοιχτό κίτρινο, σκούρο κίτρινο π
και ορτοκαλί

16. L : π
μήκος λευράς τετραγώνου (54 data points)
N : π π π π
λήθος τετραγώνων ου εριέχουν το υ ό εξέταση
χρώμα
(a)Αλουμίνιο (Blue Poles: Number 11, 1952)
(b) (π π )
Μαύρο ίνακας ενός σ ουδαστή τέχνης
(c) Μαύρο (π π )
ίνακας άγνωστης ροέλευσης
« π »
Δι λό φράκταλ (bi-fractal): παρατηρείται στο σύνολο των
πινάκων του Πόλοκ (παρατηρείται και σε ορισμένα φράκταλ στη
)
φύση
DL = 1,96
(Levy διάσταση
φράκταλ)
DD = 1,63
(dripping διάσταση
φράκταλ)
LT = 1,8 cm
(μέγεθος
μετάβασης)
DD = 1,72
(όλα τα χρώματα)
l ogN=−dlogL+b

17. Untitled,
1950
(DD = 1,89)
Autumn
Rhythm:
Number 30,
1950
(DD = 1,66)
Untitled,
1945
(DD = 1,12)
o (1943 – 1945)
Πρώιμη
χαμηλή διάσταση DD
o Μεταβατική (1946 – 1947)
πειραματισμός με την
τεχνική της έκχυσης οδηγεί
π
σε α ότομη αύξηση της
διάστασης DD
o (1948 – 1952)
Κλασική
π ( )
εραιτέρω μικρή αύξηση
της διάστασης DD
Οι φάσεις της
τεχνικής dripping
του Pollock
10 π
Τα χρόνια βελτίωσης της τεχνικής έκχυσης υ οκινήθηκαν
π π
α ό την ε ιθυμία να δημιουργήσει μοτίβα φράκταλ με
π π 1,7
διάσταση ερί ου !

18. 1,3 1,12
1,89 1,89
Untitled (1945)
Untitled (1950)

19. Πώς ζωγράφιζε ο Pollock;
• (
Νησίδες τροχιών κατανεμημένες σε όλο τον
) π 50
καμβά με μέγεθος α ό cm – 100cm .
η καθεμία
• π .
Εκτεταμένες τροχιές ου ενώνονται με τις νησίδες
• ( π π
Αργότερα έξι μήνες μετά στην ερί τωση του Blue
Poles) « π » π π
ενα οθέτει ε ι λέον στρώματα
π .
διαφορετικού χρώματος άνω στο αρχικό στρώμα
Κατά το στάδιο αυτό η διάσταση φράκταλ
π 0,05!
αυξάνεται κατά λιγότερο α ό
Η διαδικασία αυτή αυξάνει την πιθανότητα ότι τα φράκταλ
δεν είναι μια αναπόφευκτη συνέπεια της έκχυσης μπογιάς
αλλά το αποτέλεσμα της συγκεκριμένης τεχνικής έκχυσης
του Pollock (Taylor et al., 2003).

20. … π !
Δύο σημαντικές φράκταλ αρατηρήσεις
1. π π π
Το υγρό ου έφτει α οσυντίθενται σε μια
.
αλληλουχία φράκταλ σταγονιδίων
2. π π
Έχει αρατηρηθεί ότι η ανθρώ ινη κίνηση
παρουσιάζει χαρακτηριστικά φράκταλ τη
π π π
στιγμή ου ο άνθρω ος ε ανέρχεται σε
π .
ισορρο ία
Πώς ζωγράφιζε ο Pollock;
π π Pollock
Στην ερί τωση του ο
σχηματισμός σταγονιδίων φράκταλ
:
εξαρτάται
) π
α α ό τη ρευστότητα του χρώματος
και
) π π
β α ό την α όσταση της έκχυσης
Πιθανότατα οι κινήσεις του Pollock π π
ραγματο οιούνταν
π
σε μία ελεγχόμενη εκτός ισορρο ίας κατάσταση
(controlled off-balance).

21. • sd > 0,031 (Pollock: 0,009 < sd < 0,027 *)
• π π
κά οια α ό τις DD ή DL π 1,05 – 2
δεν είναι α ό
• |DD - DL|< 0,05
• DD > DL ( « π » )
αντεστραμμένο δι λό φράκταλ
* DIA Analysis 14 π
σε ίνακες του Pollock
Richard P. Taylor
 14 π
Και οι ίνακες του Pollock (που εξετάστηκαν
) π
στην έρευνα ε αληθεύουν 6
και τα κριτήρια
του Taylor!
 π π
Οι ίνακες ου δεν είναι Pollock δεν
π (
ε αληθεύουν τουλάχιστον ένα συνήθως
π ) π !
ερισσότερα α ό τα έξι κριτήρια
π π
Μ ορούμε χρησιμο οιώντας την ανάλυση φράκταλ να εξετάσουμε αν
π π
κά οιος ίνακας του Pollock ;
είναι γνήσιος
π π π
Ή μή ως όλοι οι ίνακες ου δημιουργούνται με τεχνική dripping είναι
;
φράκταλ

22. Harsh Mathur Lawrence Krauss
Katherine Jones-Smith
«Καμία πληροφορία σχετικά με τη
γνησιότητα δεν μπορεί να εξαχθεί από την
ανάλυση φράκταλ»
τεστ γνησιότητας
Taylor
2/3 πίνακες
του Pollock
π
α οτυγχάνου
!
ν στο τεστ
3/4 π π
ίνακες ου δεν
είναι
( π )
α οδεδειγμένα
Pollock περνούν το
!
τεστ
π π
Μ ορούμε χρησιμο οιώντας την ανάλυση φράκταλ να εξετάσουμε αν
π π
κά οιος ίνακας του Pollock ;
είναι γνήσιος
π π π
Ή μή ως όλοι οι ίνακες ου δημιουργούνται με τεχνική dripping είναι
;
φράκταλ

23. Δραστηριότητα: Μετράω τη διάσταση φράκταλ της ακτογραμμής της Νορβηγίας
https://www.geogebra.org/m/SRAdztNd
Δείτε τη δραστηριότητα
online

24. Μήκος πλευράς τετραγώνου: 62,5mi
Δραστηριότητα: Μετράω τη διάσταση φράκταλ της ακτογραμμής της Νορβηγίας

25. Μήκος πλευράς τετραγώνου: 31,25mi
Δραστηριότητα: Μετράω τη διάσταση φράκταλ της ακτογραμμής της Νορβηγίας
1
2 4
3
6
5
8
9
7 10
11
12
13
14
15
16
17
18
19
20
21

26. Δραστηριότητα: Μετράω τη διάσταση φράκταλ της ακτογραμμής της Νορβηγίας
Μήκος πλευράς τετραγώνου: 20,83mi

27. Δραστηριότητα: Μετράω τη διάσταση φράκταλ της ακτογραμμής της Νορβηγίας
Μήκος πλευράς τετραγώνου: 15,63mi

28. Δραστηριότητα: Μετράω τη διάσταση φράκταλ της ακτογραμμής της Νορβηγίας
Μήκος πλευράς τετραγώνου: 12,5mi

29. logN=−dlogL+b

31. π
Προσδοκώμενα Μαθησιακά Α οτελέσματα
( ) π
ΠΜΑ στο Νέο Πρόγραμμα Σ ουδών
• Αλ.Σρ.12.5. Χρησιμοποιούν τους λογαρίθμους στη μελέτη πραγματικών φαινομένων.
• Σ.Ε.12.Π.1. Με τη βοήθεια του διαγράμματος διασποράς διερευνούν την ύπαρξη γραμμικής
συσχέτισης μεταξύ των τιμών δύο ποσοτικών χαρακτηριστικών του πληθυσμού και διακρίνουν τη
θετική από την αρνητική γραμμική συσχέτιση.
• Σ.Ε.12.Π.2. Με τη βοήθεια της τιμής του συντελεστή γραμμικής συσχέτισης του Pearson σχολιάζουν
την ύπαρξη και το είδος της γραμμικής συσχέτισης μεταξύ των τιμών δύο ποσοτικών
χαρακτηριστικών του πληθυσμού.
• Σ.Ε.12.Π.4. Χαράσσουν εποπτικά την ευθεία παλινδρόμησης για το απλό γραμμικό μοντέλο και
σχολιάζουν την προσαρμογή της.
• ΑΓ.Ε.11.Π.1 Διερευνούν τον συντελεστή διεύθυνσης ευθείας, διατυπώνουν την εξίσωσή της και
αναγνωρίζουν αν μια εξίσωση είναι εξίσωση ευθείας.
• Σ.Ε.12.Π.5. Ερμηνεύουν τις τιμές των συντελεστών της ευθείας παλινδρόμησης στο πλαίσιο του
ερευνητικού ερωτήματος.
Φράκταλ, Pollock και
ακτογραμμές στη
σχολική τάξη;

32. ;
Πού
• π
Τυ ική διδασκαλία [ :
Μαθηματικά Γ΄ Λυκείου
π
Προσανατολισμού Θετικών Σ ουδών ή Γενικής
, :
Παιδείας Θεματικό Πεδίο Στατιστική]: εφαρμογή
π (π. .
στην τάξη ή εργασία για το σ ίτι χ αντί για
)
διαγώνισμα τετραμήνου
• π
Πολιτιστικό ρόγραμμα ή Όμιλος Καινοτομίας
και Δημιουργικότητας
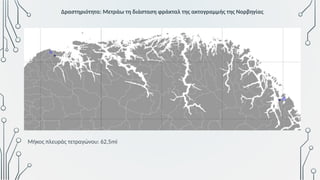
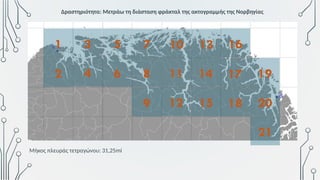
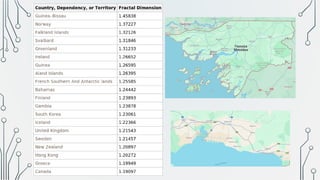
Η ΕΝΝΟΙΑ ΤΟΥ ΦΡΑΚΤΑΛ: ΑΠΟ ΤΗ ΧΙΟΝΟΝΙΦΑΔΑ ΤΟΥ
ΚΟΧ ΜΕΧΡΙ ΤΗ ΜΕΤΡΗΣΗ ΤΗΣ ΔΙΑΣΤΑΣΗΣ ΜΙΑΣ
ΑΚΤΟΓΡΑΜΜΗΣ
Φράκταλ, Pollock και
ακτογραμμές στη
σχολική τάξη;
π
Δείτε τη διδακτική ρόταση στο
Φωτόδεντρο

33. …
εντ δε γουίνερ ιζ

34. Ανδρέας Λύκος
( ) -
Μαθηματικός Πειραματικό ΓΕΛ Κομοτηνής MSc -
Στατιστικής Συγγραφέας
Πόσο φράκταλ είναι ο
Pollock;
Βόλος
π
Πανε ιστήμιο
(28
Θεσσαλίας ης
78
Οκτωβρίου )
6
Σάββατο
Ιουλίου
18:30-19:30 &19:45-20:45
Φράκταλ στον Pollock
 R.P. Taylor, R. Guzman, T.P. Martin, G.D.R. Hall, A.P. Micolich, D.
Jonas, B.C. Scannell, M.S. Fairbanks, C.A. Marlow (2005),
“Authenticating Pollock Paintings Using Fractal Geometry”, Pattern
Recognition Letters, vol. 28, 695-702.
 Taylor, R.P., Spehar, B., Wise, J.A., Clifford, C.W.G., Newell, B.R.
and Martin, T.P., (2003), “Perceptual and physiological responses to
the visual complexity of Pollock’s dripped fractal patterns”.
 R.P. Taylor (2002), “Order in Pollock’s Chaos”, Scientific American,
vol. 287, 116-121
 Katherine Jones-Smith, Harsh Mathur, Lawrence M Krauss, (2009),
“Drip paintings and fractal analysis”.
Φράκταλ στην ακτογραμμή
 Mandelbrot, B. (1967). "How Long is the Coast of Britain? Statistical
Self-Similarity and Fractional Dimension". Science. 156 (3775):
636–638.
 Mandelbrot, B. (1983). “The Fractal Geometry of Nature”. W. H.
Freeman and Co. pp. 25–33.
 Stoa, Ryan (2020). "The Coastline Paradox". Rutgers University Law
Review. 72
Ξαναδείτε την
π …
αρουσίαση