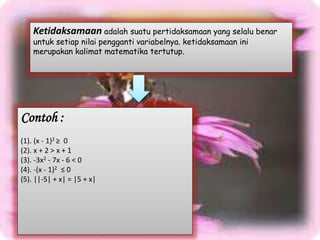
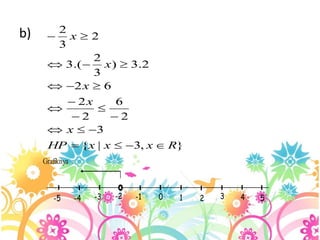Dokumen tersebut membahas tentang persamaan dan pertidaksamaan linear satu variabel. Secara singkat, persamaan adalah kalimat matematika yang menggunakan tanda sama dengan, sedangkan pertidaksamaan menggunakan tanda tidak sama dengan. Dokumen ini juga menjelaskan cara menyelesaikan persamaan dan pertidaksamaan linear dengan menambah, mengurangi, membagi, atau mengalikan bilangan pada kedua sisinya.

1. Persamaan
dan
Pertidaksamaan

2. Perhatikan ilustrasi berikut !
Sebuah kelompok sirkus mempunyai enam ekor singa; tiga jantan dan tiga betina. Jika
setiap hari pemiliknya memberikan 45 kg daging untuk makanan singa-singa tersebut dan
setiap singa mendapatkan bagian yang sama, berapakah berat daging yang dimakan oleh
setiap singa dalam sehari?
Jika tiap singa memakan daging n kg sehari, dan daging yang dimakan oleh keenam singa itu
45 kg, tulis kalimat terbuka yang berkaitan dengan berat daging yang dimakan oleh keenam
singa tersebut.
Jika seekor singa jantan makan daging dua kali yang dimakan seekor singa betina dan
daging yang dimakan keenam singa itu 36 kg, berapa kilogram daging yang dimakan tiap
singa jantan?

3. Jika dimisalkan setiap Singa makan
daging m kg, maka diperoleh
hubungan :
6 x m = 45.
Nilai m belum diketahui, oleh karena itu
m merupakan variabel atau peubah.
Kalimat terbuka 6m = 45 menggunakan
tanda “=”.

4. Jadi, apa itu
persamaan????

5. Persamaan adalah kalimat terbuka
yang menggunakan tanda “=”.

6. Jika pangkat tertinggi dari variabel pada suatu
persamaan adalah satu, maka persamaan itu disebut
persamaan linear. Persamaan linear yang hanya memuat
satu variabel disebut persamaan linear dengan satu
variabel atau persamaan linear satu variabel. Jadi, 6m =
45 merupakan salah satu contoh dari persamaan linear
dengan satu peubah.

7. Contoh lain dari persamaan
linearsatu variabel :
a. 2x + 4 = 7
b. 3 – p = 5
c. 2y + 3 = 25

8. Cara menyelesaikan persamaan linier
satu peubah
Dalam menyelesaikan persamaan linear dengan satu
peubah, langkah- langkah yang harus dilakukan adalah
:
1. Menambah kedua ruas dengan bilangan yang
sama.
2. Mengurangi kedua ruas dengan bilangan yang
sama.
3. Membagi atau mengalikan kedua ruas dengan
bilangan yang sama dan bukan nol.

9. Ganang dan Donny adalah kakak beradik. Mereka
bersepeda dari lapangan bola ke rumahnya melewati
jalan yang sama. Ganang bersepeda dengan kecepatan 12
km/jam, sedangkan Donny 8 km/jam. Ganang tiba di
rumahnya 15 menit sebelum Donny tiba. Berapa lama
Ganang bersepeda dari lapangan bola ke rumahnya ?
Contoh

10. Penyelesaian :
Diketahui: -kecepatan Ganang bersepeda dari rumah ke
lapangan bola = 12 km/jam
kecepatan Donny bersepeda dari rumah ke
lapangan bola = 8 km/jam
-waktu tiba Ganang di rumah = 15 menit sebelum donny
Ditanya: Lama Ganang bersepeda dari lapangan bola ke rumah = ....?
Jawab:
Misalkan lama Ganang bersepeda adalah t jam, maka lama Donny bersepeda
adalah
Jarak yang ditempuh Ganang sama dengan jarak yang ditempuh Donny, sehingga
Jadi, lamanya Ganang bersepeda adalah jam atau 30 menit.
jam
t
jam
t )
4
1
(
)
60
15
( 


2
1
4
2
2
4
2
8
12
2
8
12
4
1
.
8
8
12
)
4
1
(
8
)
(
12











t
t
t
t
t
t
t
t
t
t
t
2
1

11. Banyak siswa di kelas 2010 E kurang dari 40 orang. Kalimat “Banyak siswa
di kelas 2010 E kurang dari 40 orang” jika dipisahkan kata-katanya adalah
sebagai berikut :
Kata – kata
Simbol matematika
Keterangan : n = banyak siswa kelas 2010 E
n < 40
40
Kurang dari
Banyak siswa
kelas 2010 E

12. Jadi., apa itu pertidaksamaan
???

13. Pertidaksamaan adalah kalimat terbuka
yang menggunakan tanda “>”, “≥”, “<”, atau “≤”.
Pertidaksamaan yang memuat satu peubah dan pangkat
variabelnya adalah satu disebut pertidaksamaan linear (
dalam ) satu variabel.

14. Setiap pertidaksamaan memuat variabel.
Pengganti variabel yang menyebabkan kalimat
itu benar disebut penyelesaian dari
pertidaksamaan itu. Himpunan dari semua
penyelesaian disebut Himpunan Penyelesaian
dari pertidaksamaan itu.
-5 adalah penyelesaian dari pertidaksamaan
2x – 5 < -x + 2, karena 2(5) – 5 < -(-5) + 2
adalah pernyataan yang benar.
4 bukan penyelesaian dari pertidaksamaan 4t
– 12 ≥ 2t + 1, karena 4(4) – 12 ≥ 2(4) + 1adalah
pernyataan yang salah.

15. Menyelesaikan pertidaksamaan
dengan menambah atau mengurangi

16. Perhatikan pernyataan -4 < 1.
Pernyataan itu benar.
Gambar garis bilangan di bawah ini menunjukkan apa yang terjadi jika kedua ruas
ditambah dengan 2.
Gambar di atas menunjukkan bahwa -4 < 1
Jika kedua ruas ditambah 2, maka diperoleh pernyataan -2 < 3.
Pernyataan itu juga benar.
Pada contoh di atas, menambahkan dengan 2 pada kedua ruas tidak merubah
kebenaran dari pernyataan.
3
2
1
0
-1
-2
-3
-5 -4 5
4

17. Sifat menambah atau mengurangi pada
pertidaksamaan.
Contoh:
Tentukan himpunan penyelesaian dari pertidaksamaan :
a) y + 2 > 6
b) x – 3 ≤ 2, x A = {-2,-1,0,1,2,3,4,5,6,7}
Penyelesaiannya :
y + 2 > 6
y + 2 – 2 > 6 – 2 (kedua ruas dikurangi 2)
y > 4
HP = {y y > 4, y R}
Jika kedua ruas pertidaksamaan ditambah atau dikurangi dengan bilangan yang
sama, maka tanda pertidaksamaan tetap.
Grafiknya :
1 2 3 4
0
-5 5
-4 -3 -2 -1

18. b) x – 3 ≤ 2
x – 3 + 3  2 + 3 (kedua ruas ditambah 3)
 x ≤ 5
Karena x harus anggota {-2,-1,0,1,2,3,4,5,6,7}, maka
HP = {-2,-1,0,1,2,3,4,5}
Cara lain:
Karena anggota A sedikit, mancari penyelesaian dapat pula mencoba
satu persatu.
x = -2  (-2) – 3 ≤ 2
-5 ≤ 2 (benar)
x = -1  (-1) – 3 ≤ 2
-4 ≤ 2 (benar)
x = 0  (0) – 3 ≤ 2
-3 ≤ 2 (benar)
x = 1  (1) – 3 ≤ 2
-2 ≤ 2 (benar)

19. x = 2  (2) – 3 ≤ 2
-1 ≤ 2 (benar)
x = 3  (3) – 3 ≤ 2
0 ≤ 2 (benar)
x = 4  (4) – 3 ≤ 2
1 ≤ 2 (benar)
x = 5  (5) – 3 ≤ 2
2 ≤ 2 (benar)
x = 6  (6) – 3 ≤ 2
3 ≤ 2 (salah)
x = 7  (7) – 3 ≤ 2
4 ≤ 2 (salah)
Jadi, HP = {-2,-1,0,1,2,3,4,5}

20. Menyelesaikan pertidaksamaan
dengan mengalikan atau membagi

21. Pada pertidaksamaan :
•Jika kedua ruas dikalikan atau dibagi dengan
bilangan positif yang sama dan bukan nol, maka tanda
pertidaksamaannya
tidak berubah.
•Jika kedua ruas dikalikan atau dibagi dengan
bilangan negatif yang sama dan bukan nol, maka
tanda pertidaksamaannya berubah menjadi
sebaliknya.
Sifat mengalikan atau membagi ruas
pertidaksamaan

22. Contoh :
Tentukan himpunan penyelesaian dari pertidaksamaan berikut dan gambar
grafik penyelesaiannya pada garis bilangan.
a)
b)
Penyelesaian:
a)
1
2


x
2
3
2

 x
}
,
2
|
{
2
)
1
.(
2
2
.
2
1
2
R
x
x
x
Hp
x
x
x












Kedua ruas dikali 2, tanda tidak berubah
Grafiknya :
1 2 3 4
0
-5 5
-4 -3 -2 -1

23. b)
Grafiknya :
1 2 3 4
0
-5 5
-4 -3 -2 -1
}
,
3
|
{
3
2
6
2
2
6
2
2
.
3
)
3
2
.(
3
2
3
2
R
x
x
x
HP
x
x
x
x
x





















24. Kesamaan
dan
Ketidaksamaan

25. Kesamaan (equality) adalah kalimat
matematika tertutup yang menyatakan hubungan
“sama dengan”, dan berlaku untuk setiap nilai
pengganti variabelnya. Kesamaan merupakan
kalimat matematika tertutup yang nilai
kebenarannya selalu benar.

26. contoh
• (a). (2x - 1)2 = 4x2 - 4x + 1
• (b). 4x2 - 9 = (2x + 3)(2x - 3)
• (c). =||-5| + x| = |5 + x|

27. Ketidaksamaan adalah suatu pertidaksamaan yang selalu benar
untuk setiap nilai pengganti variabelnya. ketidaksamaan ini
merupakan kalimat matematika tertutup.
Contoh :
(1). (x - 1)2 ≥ 0
(2). x + 2 > x + 1
(3). -3x2 - 7x - 6 < 0
(4). -(x - 1)2 ≤ 0
(5). ||-5| + x| = |5 + x|

28. Harga mutlak

29. Harga mutlak atau nilai
mutlak adalah suatu konsep
dalam matematika yang
menyatakan selalu positif.
Secara matematis pengertian
harga mutlak dari setiap
bilangan real x yang ditulis
dengan simbol , ialah nilai
positif dari nilai x dan -x.

30. B Q C P A
-b -3 0 3 a
Jarak = 3
Jarak = 3
Jarak = -b
Jarak = a
Untuk lebih jelasnya, konsep harga mutlak dirancang dari suatu
bilangan real x, hubungannya dengan konsep jarak secara
geometri dari x ke 0.
Jarak dari titik P = 3 ke titik C = 0 adalah 3 - 0 = 3
Jarak dari titik Q = -3 ke titik C = 0 adalah 0 - (-3) = 3
Untuk a > 0, jarak dari titik A = a ke titik C = 0 adalah a - 0 = a
Untuk b < 0, jarak dari titik B = a ke titik C = 0 adalah a - b = -b
Untuk a > 0, jarak dari titik C = 0 ke titik C = 0 adalah 0.
Kesimpulan yang didapat :
Jarak x ke 0 = x, jika x 0
= -x, jika x 0.

31. Definisi Harga Mutlak
Untuk setiap bilanga real x, harga mutlak dari x ditulis |x|
dan x
|x|
Gambaran lebih jelasnya dapat kita perhatikan diagram
seperti yang ditunjukkan oleh garis bilangan berikut ini:
x , x ≥ 0
-x , x ≤ 0
x ≤ 0 x ≥ 0
0
|x| = x
|x| = -x

32. Contoh :
1. |-4|= 4
2. |-5|= -(-5) = 5

33. Sifat-Sifat Harga Mutlak
Untuk setiap bilangan real x dan y , dan c > 0 berlaku :
1. |xy| = |x||y|
2. |x| < c  -c < x < c
3. |x| > c  x > c atau x < -c

34. Daftar Pustaka
Kusrini dkk. 2008.Contextual Teaching And Learning.
Jakarta: Pusat Perbukuan
Departemen Pendidikan Nasional.
www.google.com/file.upi.edu/Direktori/FPMIPA/JUR._PE
ND._MATEMATIKA/195509091980021-
KARSO/Modul_9_S1_PGSD.Pdf