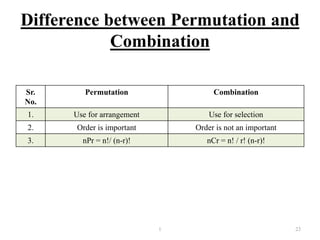
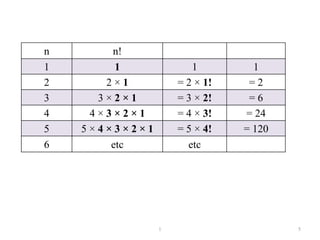
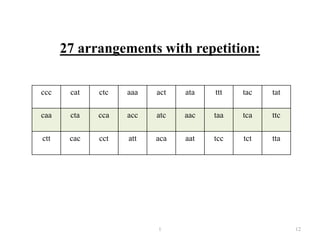
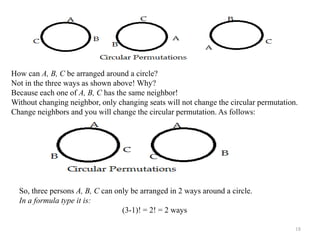
This document discusses permutation and combination concepts including: - Permutations involve arrangements where order matters, while combinations involve selections where order does not matter. - Formulas are provided for calculating permutations and combinations. - Specific types of permutations are covered such as permutations with repetition allowed/not allowed, circular permutations, and permutations when things are not all different. 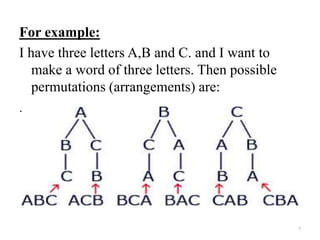- Examples are provided to demonstrate calculating permutations and combinations in different scenarios.

1. UNIT-1
Permutation and Combination
Points to be covered:
• Meaning,
• Fundamental principle of counting,
• Theorem based on permutation and
combination (without proof),
• Permutations of things not all different,
Permutation when repetition is allowed, circular
permutations,
• examples of permutation and combination.
11

2. Fundamental Principle of Counting
The rules of sum and product:
(1) The Rule of Sum:
• If a first task can be performed in m ways,
while a second task can be performed in n
ways, and the tasks cannot be performed
simultaneously, then performing either task
can be accomplished in any one of m+n ways.
21

3. (2) The Rule of Product
• If a procedure can be broken down into first
and second stages, and if there are m possible
outcomes for the first stage and if, for each of
these outcomes, there are n possible outcomes
for the second stage, then the total procedure
can be carried out, in the designated order, in
mn ways.
31

4. Factorial:
• The factorial function (symbol: !) means to
multiply a series of descending natural
numbers.
Examples:
(1) 4! = 4 × 3 × 2 × 1 = 24
(2) 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
(3) 1! = 1
1 4

5. n n!
1 1 1 1
2 2 × 1 = 2 × 1! = 2
3 3 × 2 × 1 = 3 × 2! = 6
4 4 × 3 × 2 × 1 = 4 × 3! = 24
5 5 × 4 × 3 × 2 × 1 = 5 × 4! = 120
6 etc etc
1 5

6. Permutation:
• The different arrangements of a given number
of things by taking some or all at a time, are
called permutations.
• In Permutation, ordered is an important.
• A formula for the number of possible
permutations of r objects from a set of n.
• This is usually written nPr .
6
!
( )!
n r
n
P
n r



7. For example:
I have three letters A,B and C. and I want to
make a word of three letters. Then possible
permutations (arrangements) are:
.
7

8. Important Results:
8
0
( 1) ( 1) ( 1)
1 1
1. P !
2. 1
3. .
4. .
n n
n
n r n r n r
n r n r n r
n
P
P P r P
P r P P
  
 


 
 

9. Example:
Find how many four-letter words can be formed
out of the letters of the word ‘ ARIEL’
Answer:
There are 5 different letters in the word ‘ARIEL’.
The total number of four letter words, which can
be formed out of these 5 letters
= 5P4 = 5 * 4* 3* 2 = 3024.
1 9

10. TYPES OF PERMUTATION:
(1)Repetition is allowed
(2)Repetition is not allowed
1 10

11. (1) Repetition is allowed:
(when all things are different)
Example: How many 3 letter words can be formed
using the letters c,a,t allowing for repetition of the
letters?
Solution:
For this problem, 3 locations are needed:
_____ • _____ • _____
There are 3 letters which can be used to fill the first
location. Because repetition is allowed, the same 3
letters can be used to fill the second location and also
the last location.
__3___ • __3___ • __3___ = 27
arrangements
1 11

12. 27 arrangements with repetition:
1 12
ccc cat ctc aaa act ata ttt tac tat
caa cta cca acc atc aac taa tca ttc
ctt cac cct att aca aat tcc tct tta

13. Permutations of things not all different
• The number of permutations of ‘n’ things of which ‘p’
things are alike and of one kind, ‘q’ things are alike
and of another kind, ‘r’ things are alike and of another
kind is given by
• If out of ‘n’ things, ‘r’ things are alike and of one kind
and (n-r) things are alike and of another kind, then the
total number of permutations
13
!
! ! !
n
p q r
!
!( )!
n
r n r

14. • Example:
1. How many different 5-letter words can be
formed from the word APPLE ?
Answer:
You divide by 2! because the letter P repeats
twice
14
5 5 5*4*3*2*1
60
2! 2
P
 

15. Example:
How many different words can be made out of the
word ‘ ALLAHABAD’?
Answer:
The word ‘ ALLAHABAD’ consists of 9 letters in
which A is repeated four times, L is repeated
twice and the rest are all different.
Hence the required number of word is
9! / 4!2! = (9*8*7*6*5*4!)/ 4!*2
= 7560.
15

16. (2) Repetition is not allowed
Example :
• Consider a lottery in which 6 balls are consecutively drawn at
random from an urn containing 99 balls, each printed with a
unique number 1, ..., 99. What are the total number of possible
outcomes of this draw?
Answer:
Each drawing is a permutation of 6 numbers chosen from a set of 99,
without repetition. Thus, the total number of possible permutations
is:
99P6 = 99 × 98 × 97 × 96 × 95 × 94
= 806, 781, 064, 320.
16

17. Circular Permutation
• The circular permutations are used when the
elements have to be arranged "in a circle"
order, (for example, the guests around a table
at a dinner party), so that the first element that
"is located" in the sample determines the
beginning and the end of the sample.
PCn = (n-1)!
17

18. 18
How can A, B, C be arranged around a circle?
Not in the three ways as shown above! Why?
Because each one of A, B, C has the same neighbor!
Without changing neighbor, only changing seats will not change the circular permutation.
Change neighbors and you will change the circular permutation. As follows:
So, three persons A, B, C can only be arranged in 2 ways around a circle.
In a formula type it is:
(3-1)! = 2! = 2 ways

19. Combination:
• The different groups or collections (or
selections) that can be formed out of a given set
of things by taking some or all of them at a time
(without consider to the order of their
arrangement) are called their combinations.
• In combinations, order does not matter.
• It is denoted by
19
(n, r)n r
n
or C orC
r
 
 
 

20. Where n= total numbers
r = no. of wish
20
!
!(n r)!
n n
r r
 
 
 

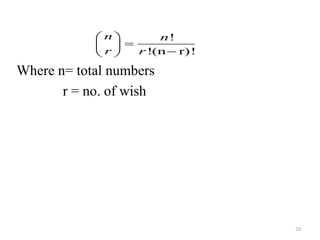
21. Important Result:
21
0
(n 1) ( 1)
1 1
1. 1
2. 1
3.
4.r. C .[ ]
5. C
n
n n
n r n n r
n r r
n r n r n r
C
C
C C
n C
C C

 
 




 

22. EXAMPLE:
How many ways can 3 men select out of 5 men.
Answer:
Here n=5 and r = 3.
By using formula
1 22
! 5! 5*4*3!
10
!( )! 3!(5 3)! 3!*2!
n
r n r
  
 

23. Difference between Permutation and
Combination
Sr.
No.
Permutation Combination
1. Use for arrangement Use for selection
2. Order is important Order is not an important
3. nPr = n!/ (n-r)! nCr = n! / r! (n-r)!
1 23

24. References:
• Sile-2,3: www.mgt.ncu.edu.tw/~ylchen/dismath/chap01.pp
• Slide-4,5: www.mathsisfun.com/numbers/factorial.html
• Slide-6: http://www.indiabix.com/aptitude/permutation-and-combination/formulas
• IMAGE-1-SLIDE-7:
https://www.google.co.in/search?hl=en&site=imghp&tbm=isch&source=hp&biw=13
66&bih=643&q=PERMUTATION&oq=PERMUTATION&gs_l=img.3..0l10.2088.59
09.0.6413.11.11.0.0.0.0.492.671.0j1j4-
1.2.0.msedr...0...1ac.1.60.img..9.2.670.3cYXg9YGhvo#facrc=_&imgdii=_&imgrc=U
TWyBH6hERKNgM%253A%3BkA_jTOu4e4nicM%3Bhttp%253A%252F%252Fw
ww.mathwarehouse.com%252Fprobability%252Fimages%252Fmultiplication-
principle4.gif%3Bhttp%253A%252F%252Fwww.mathwarehouse.com%252Fprobabil
ity%252Fpermutations-repeated-items.php%3B448%3B201
• Slide 11-12: www.regentsprep.org/regents/math/algebra/apr2/LpermRep.htm
• Slide-17: http://www.vitutor.com/statistics/combinatorics/circular_permutations.html
• Slide-18: http://www.math-for-all-grades.com/CircularPermutation.html
• Business Mathematics by G.C. Patel and A.G. Patel by atul prakashan
1 24