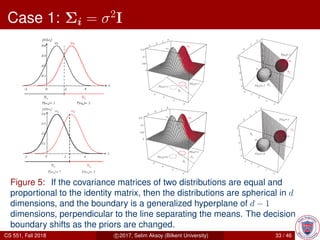
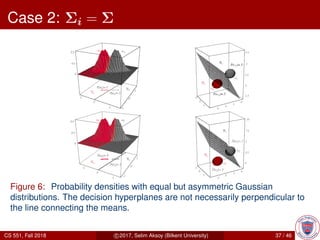
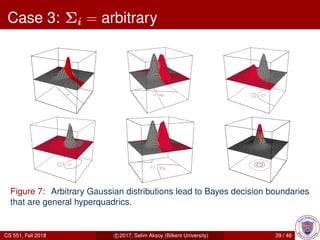
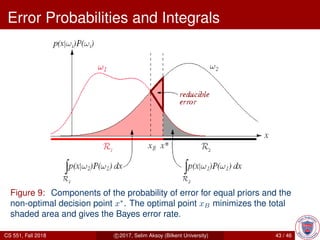
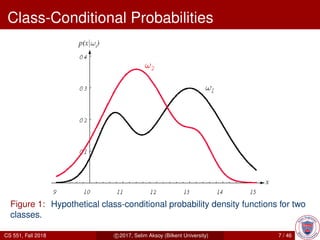
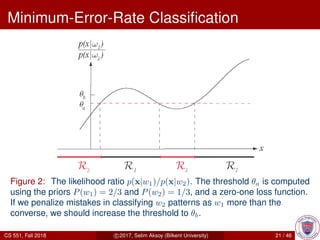
This document provides an overview of Bayesian decision theory. It begins by defining Bayesian decision theory as a statistical approach that quantifies the tradeoffs between decisions using probabilities and costs. It then discusses using Bayesian decision theory to classify fish by type based on observed features and probabilities. The document explains key Bayesian concepts like prior and posterior probabilities, conditional probabilities, discriminant functions, and how the Gaussian distribution relates to Bayesian classification. The overall summary is that Bayesian decision theory provides a framework for making optimal decisions under uncertainty by accounting for probabilities and costs associated with different outcomes.






















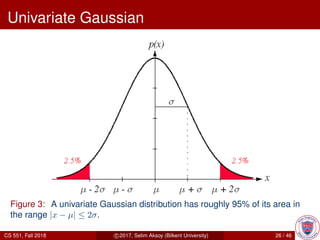
![Univariate Gaussian
For x ∈ R:
p(x) = N(µ, σ2
)
=
1
√
2πσ
exp −
1
2
x − µ
σ
2
where
µ = E[x] =
∞
−∞
x p(x) dx,
σ2
= E[(x − µ)2
] =
∞
−∞
(x − µ)2
p(x) dx.
CS 551, Fall 2018 c 2017, Selim Aksoy (Bilkent University) 25 / 46](https://image.slidesharecdn.com/patternbaysin-190619115437/85/Pattern-baysin-25-320.jpg)
![Multivariate Gaussian
For x ∈ Rd
:
p(x) = N(µ, Σ)
=
1
(2π)d/2|Σ|1/2
exp −
1
2
(x − µ)T
Σ−1
(x − µ)
where
µ = E[x] = x p(x) dx,
Σ = E[(x − µ)(x − µ)T
] = (x − µ)(x − µ)T
p(x) dx.
CS 551, Fall 2018 c 2017, Selim Aksoy (Bilkent University) 27 / 46](https://image.slidesharecdn.com/patternbaysin-190619115437/85/Pattern-baysin-27-320.jpg)