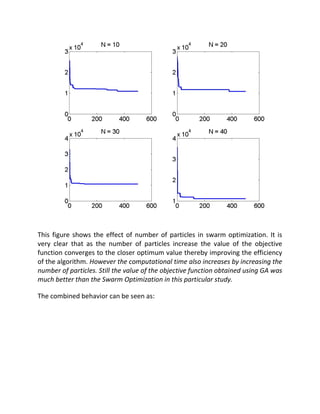
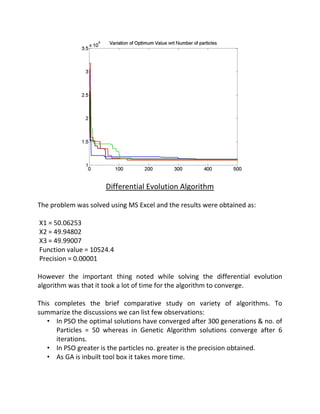
The document presents a comparative study of genetic algorithms (GA) and particle swarm algorithms (PSO) for optimizing production costs in a manufacturing firm supplying refrigerators. The analysis includes problem constraints, objective functions, and methods used, revealing that the GA achieved a cost function value of 10504.8 after 6 iterations, while PSO converged to its optimal solution after 300 generations. Observations note that while GA yields better results in terms of cost efficiency, it is generally quicker than PSO, and increasing particle numbers in PSO improves precision but requires more computational time.

1. Optimization Project
Comparative study of Genetic Algorithm and
Particle Swarm Algorithm to optimize the cost
of production for a manufacturing firm

2. Problem Statement:
This is basically a cost optimization problem where a manufacturing firm has
entered into the contract to supply 50 refrigerators at the end of the first month,
50 at the end of the second month and 50 at the end of third. The cost of
producing x refrigerators in any month is given by $ (x2
+ 1000). The firm can
produce more number of refrigerators and can carry them to subsequent month.
It cost $20 per unit for any refrigerator to be carried from one month to the next
one.
Objective function:
Total Cost = Production Cost + Holding Cost
Let the number of refrigerators produced in first month = x1
Similarly the number produced in second month = x2
In third month = x3
Total cost = (x1
2
+ 1000) + (x2
2
+ 1000) + (x3
2
+ 1000) +20* (x1 - 50) + 20*(x1 + x2 -
100)
So the cost function becomes: x1
2
+ x2
2
+ x3
2
+ 40x1 + 20x2
Constraint Function:
 x1 -50 > = 0
 x1 + x2 -100 > = 0
 x1 + x2 + x3 -150 >=0
Aim of the Project:

3. The above problem has been taken up from book on Engineering Optimization by
Dr S.S. Rao.
The problem has been solved using two methodologies
 Classical Method
 Kuhn Tucker Method
 Non Classical method
 Genetic Algorithm
 Particle Swarm Algorithm
 Differential Evolution Algorithm
The solution of the problem obtained using the Kuhn Tucker condition was
x1= 50; x2 = 50; x3 = 50
The main purpose of our project is to compare the Non Classical methods.
Genetic Algorithm
MATLAB optimization toolbox was used to get the optimum value objective
function. For the purpose two .m files were made one containing the fitness
function and the other containing the constraint equations. Optimization toolbox
was used with the default initial population of 50. Comparison results are
presented using various selection methods which were covered in lecture class.

4. The functional evaluation during different generations is also presented here:
The optimized value of the cost function obtained was 10504.8 after using GA
where the classical method gave the value equal to 10500. By running several trial
with different initial population sizes the value improved and the optimum value
was more closer to 10500.
Particle Swarm Algorithm
The algorithm works on the principle of personal best and global best approach
and tries to capture the behavior of flocking birds in search of food. The algorithm
was coded to satisfy the constraints by modifying the existing code provided by Dr
Rajib Bhattacharya (Course Instructor: Optimization Methods). The code is given
below as:
clear all;
close all;
for p = 1:4
tm = cputime;
Generation f(x) constraint
1 1851.1 0
2 13441.6 0
3 10427.4 0
4 10498.7 0
5 10504.4 0
6 10504.8 0

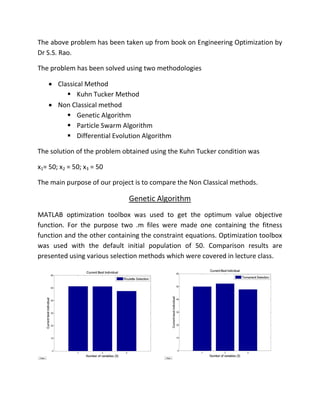
5. numPart = 5; % number of particles
numVar =3; % Number of variables
fileName = 'objfunc';
w = 0.5; % Inertia weight
C1 = 2; % learning factor for local search
C2 = 2; % learning factor for local search
maxGen =500; % Maximum generation
lb = 50; % Lower bound of the variables
ub = 180; % Upper bound of the variables
X = lb + (ub-lb)*rand(numPart,numVar); % initialize X
V = lb + (ub-lb)*rand(numPart,numVar); % initialize V
for i=1:numPart
% f(i)=fitness(X(i,:));
f(i)=feval(fileName,X(i,:));
end
X = [V X f'];
Y = sortrows(X,2*numVar+1);
pbest = Y;
gbest = Y(1,:);
for gen=1:maxGen % generation loop
for part=1:numPart % Particle loop
for dim=1:numVar % Variable loop
V(part,dim)=w*V(part,dim)+C1*rand(1,1)*(pbest(part,numVar+dim)-
X(part,numVar+dim))+C2*rand(1,1)*(gbest(numVar+dim)-X(part,numVar+dim));
X(part,numVar+dim)=X(part,numVar+dim)+V(part,dim);
end
while(X(part,numVar + 1)< 0 || X(part,numVar + 2)< 0 || X(part,numVar
+ 3)<0 || X(part,numVar + 1) - 50 <= 0 || X(part,numVar + 1) + X(part,numVar
+ 2)-100 <= 0 || X(part,numVar + 1) + X(part,numVar + 2) + X(part,numVar +
3) -150 <=0)
for dim=1:numVar % Variable loop
V(part,dim)=w*V(part,dim)+C1*rand(1,1)*(pbest(part,numVar+dim)-
X(part,numVar+dim))+C2*rand(1,1)*(gbest(numVar+dim)-X(part,numVar+dim));
X(part,numVar+dim)=X(part,numVar+dim)+V(part,dim);
end
end
%
% fnew = fitness(X(part,numVar+1:numVar+dim));
fnew = feval(fileName,X(part,numVar+1:numVar+dim));
X(part,2*numVar+1)=fnew;
if (fnew<X(part,2*numVar+1))
pbest(part,:)=X(part,:);
end
end

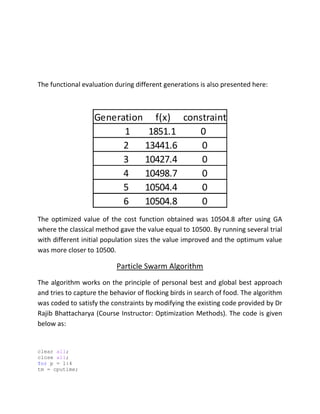
6. Y = sortrows(X,2*numVar+1);
if (Y(1,2*numVar+1)<gbest(2*numVar+1))
gbest=Y(1,:);
end
first_var(gen) = gbest(4);
second_var(gen) = gbest(5);
third_var(gen) = gbest(6);
obj_value(gen,p) = gbest(7);
disp(['Generation ', num2str(gen)]);
disp(['Best Value ', num2str(gbest(numVar+1:2*numVar+1))]);
end
numPart = numPart + 15;
end
generations = 1:500;
% subplot(2,2,1)
% plot(generations,obj_value(:,1))
% hold on
% subplot(2,2,2)
% plot(generations,obj_value(:,2))
% hold on
% subplot(2,2,3)
% plot(generations,obj_value(:,3))
% hold on
% subplot(2,2,4)
% plot(generations,obj_value(:,4))
plot(generations,obj_value(:,1),'b',generations,obj_value(:,2),'g',generation
s,obj_value(:,3),'k',generations,obj_value(:,4),'r')
cpu_time = cputime-tm ;
The modified part has been highlighted above and based on the above code some
of the results were plotted which are shown as:

7. The graph shows how the values are evolved after each generation the code is
run. The constraints are always taken care of because of the highlighted
condition. The above suggests that the value are converged after 300 generations
and this being the major difference between Swarm Optimization and GA where
the values were getting converged quickly after the 6th
generation itself.

8. This figure shows the effect of number of particles in swarm optimization. It is
very clear that as the number of particles increase the value of the objective
function converges to the closer optimum value thereby improving the efficiency
of the algorithm. However the computational time also increases by increasing the
number of particles. Still the value of the objective function obtained using GA was
much better than the Swarm Optimization in this particular study.
The combined behavior can be seen as:

9. Differential Evolution Algorithm
The problem was solved using MS Excel and the results were obtained as:
X1 = 50.06253
X2 = 49.94802
X3 = 49.99007
Function value = 10524.4
Precision = 0.00001
However the important thing noted while solving the differential evolution
algorithm was that it took a lot of time for the algorithm to converge.
This completes the brief comparative study on variety of algorithms. To
summarize the discussions we can list few observations:
• In PSO the optimal solutions have converged after 300 generations & no. of
Particles = 50 whereas in Genetic Algorithm solutions converge after 6
iterations.
• In PSO greater is the particles no. greater is the precision obtained.
• As GA is inbuilt tool box it takes more time.