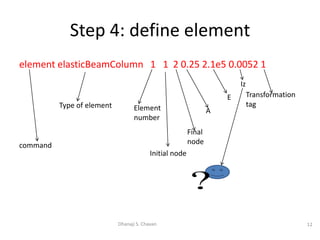
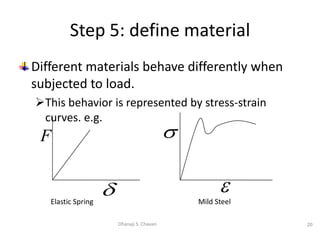
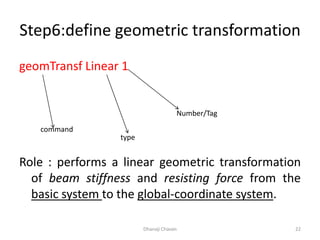
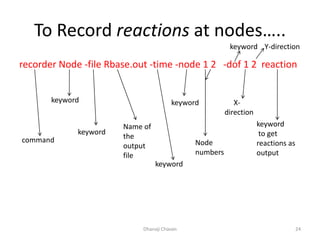
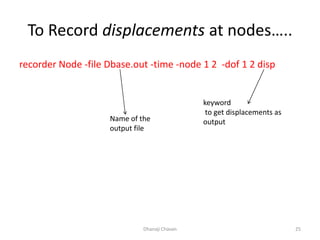
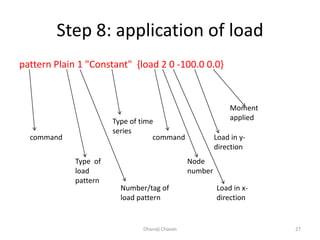
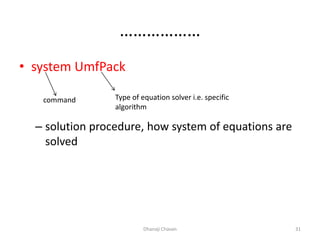
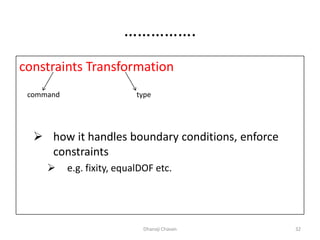
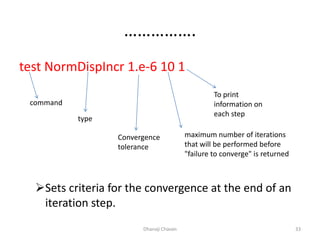
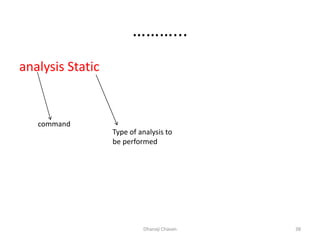
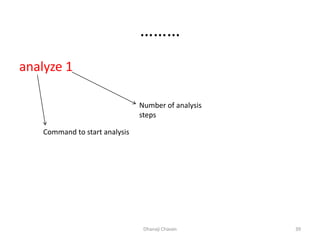
This document provides steps for modeling and performing static analysis in OpenSees. It begins with general steps like defining nodes, elements, materials, boundary conditions, and analysis objects. Then it provides an example of coding for a cantilever beam problem in OpenSees. Key steps in the example include defining two nodes, fixing the first node, using an elastic beam column element, applying a point load, and running the analysis to obtain the deflection of the free end. The document also discusses considerations for choosing appropriate elements and defines terms used in finite element modeling like degrees of freedom.

1. Modeling & Performing Static
Analysis in OpenSees
By
Dhanaji S. Chavan, Assistant Professor, TKIET, Warananagar
Dhanaji Chavan 1

2. General steps to be followed…
i. Define ndm & ndf
ii. Define nodes
iii. Define element(s)
iv. Define material(s)
v. Define boundary conditions
vi. Define matrix transformation
vii. Apply load
viii. Define recorders
ix. Define analysis objects
x. Run the analysis
Dhanaji Chavan 2

3. Example 1- Cantilever Beam
• What is the deflection of the free end of a 3 m
cantilever beam subjected to a point load of 100 kN?
(E =2*1005 kN/m2 ,c/s:0.3mx0.3m)
How to do coding for this problem in OpenSees?????
Dhanaji S. Chavan 3
3m
100kN

4. wipe
model basic -ndm 2 -ndf 3
• wipe :
clears the previous coding present in OpenSees memory, if any
• model basic :
key word to start the definition of model
• ndm :
defines number of dimensions of the problem
• ndf :
defines the degrees of freedom at a node in a model
4Dhanaji S. Chavan
Tcl script for OpenSees starts now………
step 1: define ndm & ndf

5. • ndm: number of dimensions
we have to specify whether problem is 2-dimensional or
3-dimensional.
How to determine whether problem is 2-D or 3-D:
If to specify the geometry of the problem only two coordinates x
and y are required , it is 2-D problem
If to specify the geometry of the problem three coordinates x,y
and z are required , it is 3-D problem
In present case ndm is 2
5Dhanaji S. Chavan
How to determine ndm & ndf……….

6. • We have to specify degree of freedom at a node
What is degree of freedom?
 The number unknowns ,to be determined, at a node is called as
degree of freedom
 In present case: three unknowns are there at each node
i. translation in x direction
ii. Translation in y direction
iii. Rotation
 In present case dof is 3
6Dhanaji S. Chavan
………..

7. node 1 0 0
node 2 3 0
7Dhanaji S. Chavan
Step2: define nodes
Command to
define node
Node number
X coordinate of
node
Y coordinate of
node

8. In finite element method we discretize the
given domain(geometry) into certain number
of finite elements.
in our case 3 m long beam is the domain
in present case let’s use only one element for sake
of simplicity.
The ends of an element in finite element
method are called as nodes
8Dhanaji S. Chavan
…………
1 2
(0,0) (3,0)

9. • If we assume origin at node 1, the coordinates
for node 1 and 2 are as under:
 1(0,0) & 2(3,0)
9Dhanaji S. Chavan
……….

10. fix 1 1 1 1
10Dhanaji S. Chavan
Step 3: boundary conditions
Command to
define fixity
Node number
Constrain x-translation
Constrain y-translation
Constrain rotation 

11. • In our case boundary condition is : node 1 is
fixed i.e.
No translation in x direction
No translation in y direction
No rotation
11Dhanaji S. Chavan
…………………

12. element elasticBeamColumn 1 1 2 0.25 2.1e5 0.0052 1
12Dhanaji S. Chavan
Step 4: define element
command
Type of element Element
number
Initial node
Final
node
A
E
Iz
Transformation
tag
?

13. • Which finite element to use to model the behavior of
beam? Why?
• OpenSees has wide range of elements in its library
• Is it fine if we use any element from it?
• Or we have to choose certain element only
• How to decide which element to use ?
…………..Needs some thinking…@ FEM…????????
13Dhanaji S. Chavan
………………

14. 1-d element :
Used for geometries for which one of the dimensions
is quite larger than rest two.
E.g. beam : in case of beam its length is considerably larger
than its breadth and depth. i.e. x >>> y, z
In FEM such geometry is represented by just a line. When
the element is created by connecting two nodes, software
comes to know about only one out of 3 dimensions.
Remaining two dimensions i.e. cross sectional area must be
defined as additional input data & assigned to respective
element.
14Dhanaji S. Chavan
Three types of elements in finite
element method

15. 2-d element:
Two dimensions are quite larger than third one
E.g. metal plate: length & width are considerably
larger than thickness. i.e. x, y >>> z
The third dimension i.e. thickness has to be
provided as additional input in coding by user &
assigned to respective element.
15Dhanaji S. Chavan
……..

16. 3-d element:
All three dimensions are comparable
E.g. brick: x~y~z
No additional dimension to be defined. While
meshing itself all three dimensions are
included.
16Dhanaji S. Chavan
………

17. • In our case, we understood that we have to use
1-d element.
• Which 1-d element should we use?
Should we use spring element?
Or bar/truss element?
Or beam element
Think……………….?????????????
17Dhanaji S. Chavan
…………

18. In present case,
– Shear force &
– Bending moment
will be developed in the cantilever beam.
We have to choose 1-d finite element in such a way
that it will take both shear force & bending moment
18Dhanaji S. Chavan
………..

19. We can not use spring or bar element because
Spring element models axial load only
Bar elements model axial load and axial stress
However beam element takes axial, shear &
bending stresses. Hence….
19Dhanaji S. Chavan
………

20. Different materials behave differently when
subjected to load.
This behavior is represented by stress-strain
curves. e.g.
20Dhanaji S. Chavan
Step 5: define material
Elastic Spring


Mild Steel
F


21. ……….
• In present case material has been defined
implicitly.(slide no:12)
• However in many other cases we have to
define material separately
Dhanaji Chavan 21

22. Step6:define geometric transformation
geomTransf Linear 1
Role : performs a linear geometric transformation
of beam stiffness and resisting force from the
basic system to the global-coordinate system.
Dhanaji Chavan 22
command
type
Number/Tag

23. Step 7: define recorders
• Purpose: to get results of analysis as an output
such as……..
i. Reaction
ii. Displacement
iii. Force
iv. stiffness
Dhanaji Chavan 23

24. To Record reactions at nodes…..
recorder Node -file Rbase.out -time -node 1 2 -dof 1 2 reaction
Dhanaji Chavan 24
command
keyword
keyword
Name of
the
output
file
keyword
keyword
Node
numbers
keyword
X-
direction
Y-direction
keyword
to get
reactions as
output

25. To Record displacements at nodes…..
recorder Node -file Dbase.out -time -node 1 2 -dof 1 2 disp
Dhanaji Chavan 25
Name of the
output file
keyword
to get displacements as
output

26. To Record force in element…..
• recorder Element -file ele_Lfor.out -time -ele 1 localForce
• recorder Element -file ele_Gfor.out -time -ele 1 globalForce
Dhanaji Chavan 26
Name of the
output file
keyword
to get local force as output
Name of the
output file
keyword
to get local force as output

27. Step 8: application of load
pattern Plain 1 "Constant" {load 2 0 -100.0 0.0}
Dhanaji Chavan 27
command
Type of
load
pattern
Number/tag of
load pattern
Type of time
series
command
Node
number
Load in x-
direction
Load in y-
direction
Moment
applied

28. Pattern……
• Defines the way time series, load & constraints
are applied. E.g.
i. pattern Plain: ordinary pattern
ii. pattern UniformExcitation- transient analysis
Dhanaji Chavan 28

29. Time series
• Constant: load is constant throughout the
analysis
• Linear: load varies linearly with time
• Sine : sinusoidal variation of load
Dhanaji Chavan 29

30. Step 9: defining analysis commands
system UmfPack
constraints Transformation
test NormDispIncr 1.e-6 200 1
Algorithm Newton
numberer RCM
integrator LoadControl 1 1 1 1
analysis Static
analyze 1
Dhanaji Chavan 30

31. ………………
• system UmfPack
– solution procedure, how system of equations are
solved
Dhanaji Chavan 31
command Type of equation solver i.e. specific
algorithm

32. …………….
constraints Transformation
 how it handles boundary conditions, enforce
constraints
 e.g. fixity, equalDOF etc.
Dhanaji Chavan 32
command type

33. …………….
test NormDispIncr 1.e-6 10 1
Sets criteria for the convergence at the end of an
iteration step.
Dhanaji Chavan 33
command
type
Convergence
tolerance
maximum number of iterations
that will be performed before
"failure to converge" is returned
To print
information on
each step

34. ………..
Algorithm Newton
uses the Newton-Raphson method to advance to
the next time step.
The tangent is updated at each iteration
Recommendation: numerical methods for
engineers by Chapra
Dhanaji Chavan 34
command type

35. ……….
numberer RCM
how degrees-of-freedom are numbered
Dhanaji Chavan 35
command type

36. …………
integrator LoadControl $dLambda1 <$Jd $minLambda
$maxLambda>
 $dLambda1:
•
– determine the predictive step for time t+dt
– specify the tangent matrix at any iteration
Dhanaji Chavan 36
type
DOF
Pseudo-time
step
Subsequent
time increment

37. …………..
integrator LoadControl $dLambda1 <$Jd
$minLambda $maxLambda>
$dLambda1:
- first load-increment factor (pseudo-time step)
- Usually same is followed further
<$Jd:
- must be integer
-factor relating load increment at subsequent time steps
minLambda, maxLambda:
-decides minimum &maximum time increment bound
- optional, default: $dLambda1 for both
Dhanaji Chavan 37

38. ………...
analysis Static
Dhanaji Chavan 38
command
Type of analysis to
be performed

39. ………
analyze 1
Dhanaji Chavan 39
Command to start analysis
Number of analysis
steps

40. Ex. 2: Quad element
model BasicBuilder -ndm 2 -ndf 2
Dhanaji Chavan 40

41. Material has to be defined separately
nDMaterial ElasticIsotropic $matTag $E $v
Dhanaji Chavan 41

42. Assign material to element……..
element quad $eleTag $iNode $jNode $kNode $lNode $thick
$type $matTag <$pressure $rho $b1 $b2
Dhanaji Chavan 42

43. Recorders…
recorder Element -ele 3 -time -file stress1.out -dT 0.1 material 3
stress
Dhanaji Chavan 43

44. ……….
recorder Element -ele 3 -time -file strain1.out -
dT 0.1 material 1 strain
Dhanaji Chavan 44