OpenNLP - MEM and Perceptron

OpenNLPにおける最大
エントロピー法とパー
セプトロンによる機械
学習
関口宏司＠ロンウイット

OpenNLPの分類アルゴリ
ズム
opennlp.maxent
最大エントロピー法
多クラスロジスティック回帰

opennlp.perceptron
パーセプトロン

Copyright © 2012 RONDHUIT All rights reserved

最大エントロピー法
問題解決
ゼロ頻度問題→スムージング
パラメータ数の増大、訓練データの断片化

与えられた制約の下でエントロピーを最大化す
るようなモデルを推定する

確率的言語モデルのパラメータ推定
訓練データ
……………
……
……………
標本
……
……………

確率的言語モデルのエントロピーを最大化

MEM: 英語-仏語翻訳の例
英単語"in"に対応する仏語の単語またはフレーズ
の制約
p(dans)+p(en)+p(à)+p(au cours de)+p(pendant) =
1
↓
p(dans)+p(en) = 3/10
1
↓
p(dans)+p(en) = 3/10
1
p(dans)+p(à) = 1/2

MEM
以下の2つの問題に解答を与える
言語モデルの一様さをどのようにして測るか？
与えられた制約の下で、もっとも一様な言語モデ
ルをどのようにして求めるか？

与えられた制約を満たすモデルの中でエントロ
ピーを最大にするモデルを解として与える


MEM: 確率過程
有限集合Yのメンバーyを生成する確率過程

文脈の有限集合X

全条件付き確率分布の集合P


MEM: 訓練データ
訓練データの収集

経験的確率分布
C(x,y) : 訓練データ中にペア(x,y)が出現した回数


MEM: 素性関数と制約
素性関数； 2値関数

経験的確率分布についてのfの期待値

モデルp(y|x)についてのfの期待値

制約（等式）


最大エントロピー原理
言語モデルのエントロピーH(p)

最大エントロピー原理
C: 制約等式を満たすモデルの集合
制約条件付きの最適化問題

モデルのパラメトリック形式（次ページに続
く）
λiは素性fiに対する重要性を表す


モデルのパラメトリック形
式

以下を満たすパラメータΛ*を求めればよい：


反復スケーリング法
1. Λ={λ1,…,λn}に適当な初期値を与える

2. 次式を解くことでΛの増分Δλiを求める

3. Λの値を更新する

4. Λの値が収束していなければ2.に飛ぶ


MEM: まとめ
訓練データから確率的言語モデルを推定するが、
制約条件を満たすモデルは無限に考えられる

制約条件を満たすモデルの中から最適な（＝エ
ントロピーが最大となるもの）p*を選ぶ

p*を選ぶ代わりにモデルをパラメトリック形式に
置き換えてΨ(Λ)が最大になるΛ*を求める

Λ*を求める反復スケーリング法アルゴリズムが
ある
OpenNLPは拡張反復スケーリング法（GIS)を実
装

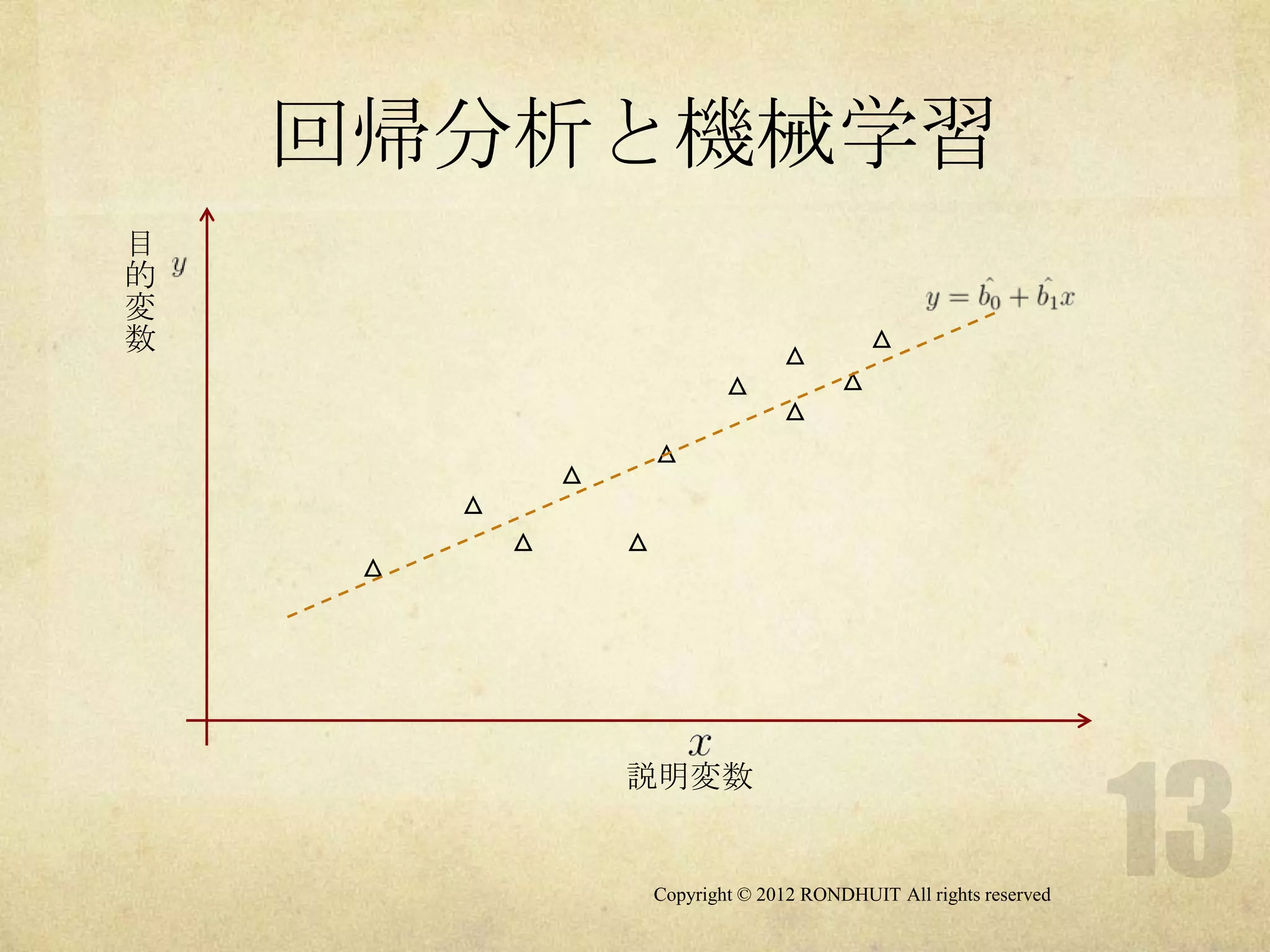
回帰分析と機械学習
目
的
変
数 △
△
△ △
△
△
△
△
△ △
△

説明変数


ニューラルネットワーク
機械学習におけるニューラルネットワーク
生物の神経組織の挙動をモデル化→セルと結合
刺激伝達

強化

抑制

入出
力 : : : 力
: : :

入力層中間層出力層

ニューロセル
ニューロセル
x1
w1 xi : 入力
z wi : 重み（結合荷重）
x2 w2 v
v : 閾値
: wn z : 出力
xn

出力関数 f(u)
ステップ関数

シグモイド関数


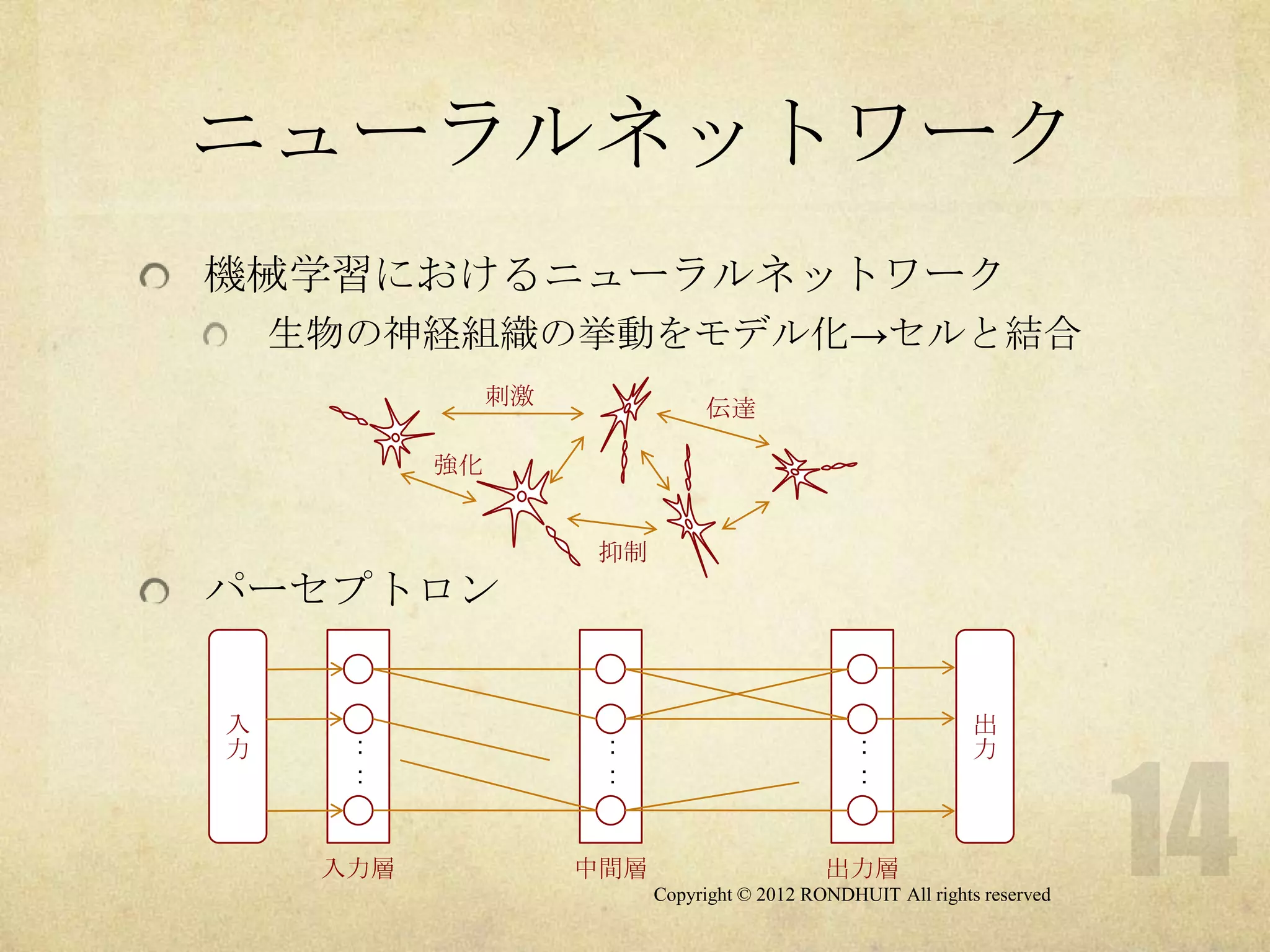
ニューラルネットワークの
構成
フィードフォワードネットワーク
階層型
入力層から出力層へ向けて信号が伝搬

リカレントネットワーク
あるニューロセルの出力がフィードバックされて、
自分自身の入力となる
ホップフィールドモデル


入力層から中間層への結合荷重と閾値は乱数で
決定

中間層から出力層への結合荷重と閾値は学習で
変更

線形分離不可能問題
→ 入力層から中間層への結合荷重も変更
→ バックプロパゲーション


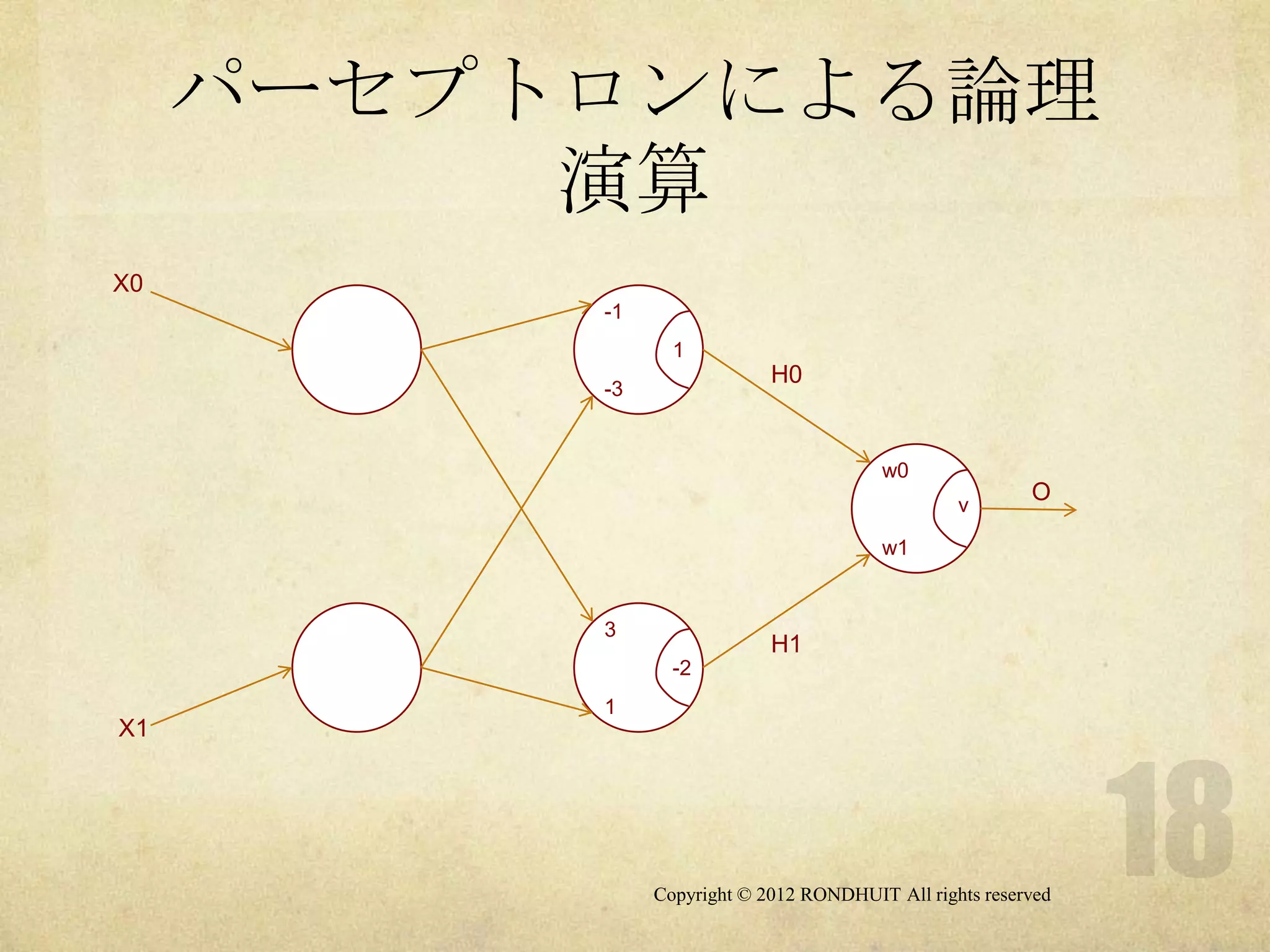
パーセプトロンによる論理
演算
X0
-1
1
H0
-3

w0
v
O

w1

3
H1
-2
1
X1


パーセプトロンによる論理
演算
論理積(w0=-77, w1=118, v=114)
X0 X1 H0 H1 O
0 0 0.268941421 0.880797078 4.31353E-14
0 1 0.01798621 0.952574127 0.048282862
1 0 0.119202922 0.993307149 0.00255185
1 1 0.006692851 0.997527377 0.960565494

論理和(w0=-27, w1=8, v=2)
X0 X1 H0 H1 O
0 0 0.268941421 0.880797078 0.098407843
0 1 0.01798621 0.952574127 0.994147201
1 0 0.119202922 0.993307149 0.938657532
1 1 0.006692851 0.997527377 0.996980115


パーセプトロンの学習手続
き
収束するまで以下を繰り返す
訓練データセットの中の一例（xi, o)について以下
を計算する
(xi)を用いて中間層の出力hiを計算する
hiを用いて出力層の出力Oを計算する
出力層のニューロセルについて、以下の計算で結合
荷重を補正する

αは適当な正の数値


OpenNLPによる機械学習
OpenNLPの準備
# パッチを当てる必要があるので、trunkからダウンロード
$ mkdir work; cd work
$ svn co http://svn.apache.org/repos/asf/opennlp/trunk OPENNLP
$ cd OPENNLP

# パッチを適用
$ wget https://issues.apache.org/jira/secure/attachment/12533987/OPENNLP-516.patch
$ patch –p0 < OPENNLP-516.patch
patching file opennlp-maxent/samples/sports/CreateModel.java

# ビルド
$ cd opennlp
$ mvn install


OpenNLPサンプルの利用
サンプルプログラム
java CreateModel [-perceptron][-real]
<filename>.dat
java Predict[-perceptron][-real] <filename>.test

サンプルデータ
football.dat/football.test
gameLocation.dat/gameLocation.test
realTeam.dat/realTeam.test
モデル
*Model.txt
訓練データ Create
Predict 結果（クラス）
*.dat Model テスト
*.test


参考文献
[1] A Maximum Entropy Approach to Natural Language
Processing, Adam L. Berger, et al., 1996 Association for
Computational Linguistics, Volume 22, Number 1
[2] 言語と計算 (4) 確率的言語モデル北研二 (著), 辻井潤一
(著) 東京大学出版会 978-4130654043
[3] はじめての機械学習小高知宏 (著) オーム社 978-
4274068461
[4] Taming Text, Grant S. Ingersoll, Thomas S. Morton, and
Andrew L. Farris, Manning Publications Co.
[5] Foundations of Statistical Natural Language Processing
Christopher Manning (著), Hinrich Schuetze (著) The MIT
Press 978-0262133609


OpenNLP - MEM and Perceptron

More Related Content

Similar to OpenNLP - MEM and Perceptron

More from Koji Sekiguchi

Recently uploaded

OpenNLP - MEM and Perceptron