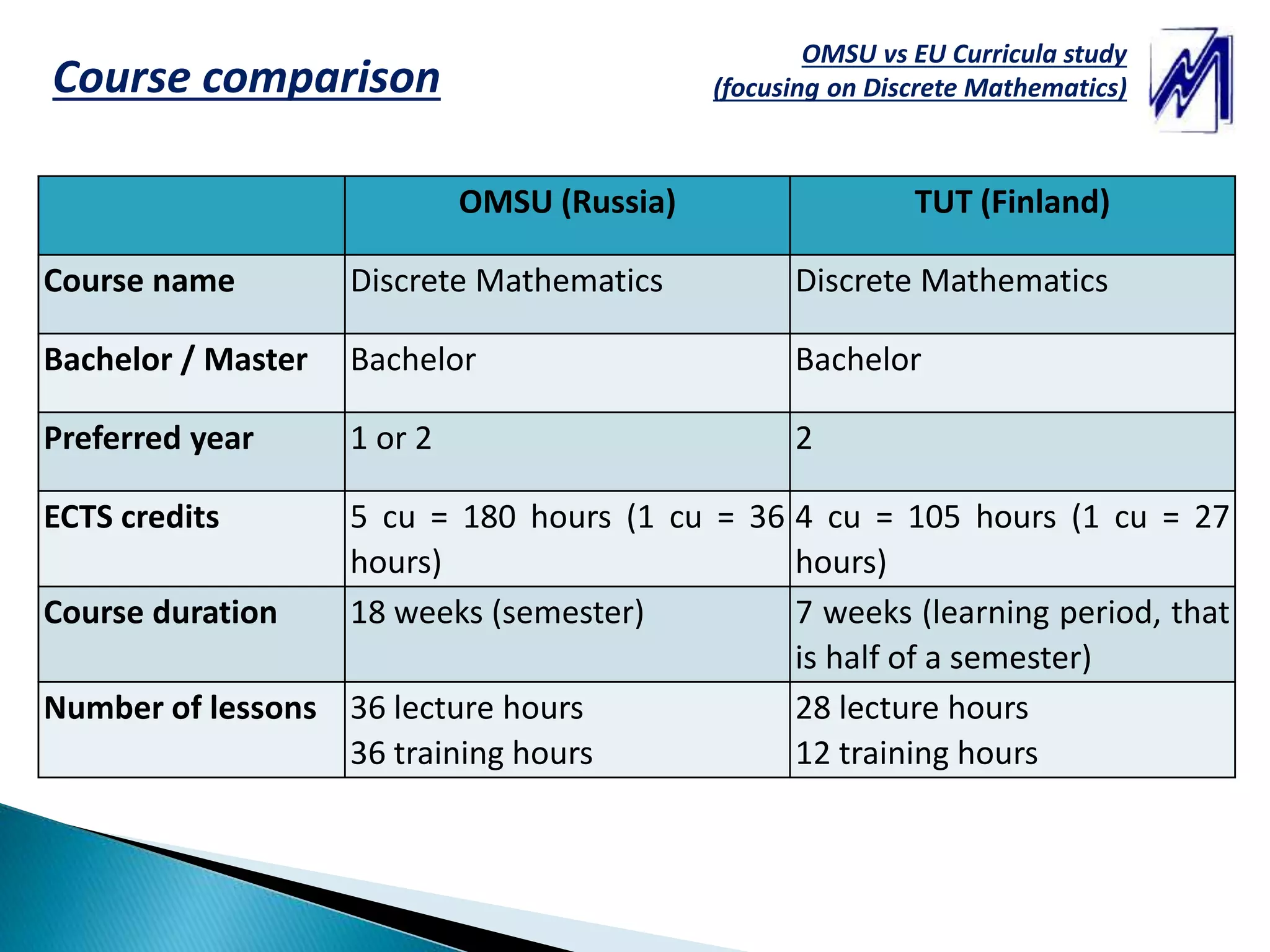
This document compares the Discrete Mathematics curricula and courses between OMSU (National Research Ogarev Mordovia State University) in Russia and TUT (Tampere University of Technology) in Finland. It analyzes the competencies, topics, and learning outcomes covered in the Discrete Mathematics courses based on three levels of difficulty. Overall, the OMSU course covers more topics like set theory, combinatorics, algebraic structures, and coding theory over a longer duration, while the TUT course focuses more on number theory over a shorter period. The document proposes increasing engineering applications and using an online learning system to help modernize the Discrete Mathematics courses.

1. NATIONAL RESEARCH OGAREV MORDOVIA STATE UNIVERSITY
OMSU vs EU comparative curricula study
Based on Discrete Mathematics courses comparison between OMSU and TUT

2. The notation of competences
OMSU vs EU Curricula study
(focusing on Discrete Mathematics)SEFI study
CORE 0
• Proof (Analysis and Calculus): prerequisite.
It is in Russian math educational tradition to pay much attention to reasoning,
thinking and proving. The motto is not “Know how”, but “Know why”.
• Sets: all competences are target.
But some students may know the basic notions and concepts from school if
there was an advanced math education.
Prerequisite Target Missing
All competences except specially mentioned ones are from “Discrete
Mathematics” SEFI area

3. OMSU vs EU Curricula study
(focusing on Discrete Mathematics)SEFI study
LEVEL 1
• Mathematical logic: all competences are missing.
There is a special mandatory course “Mathematical logic and theory of
algorithms” which is provided after Discrete Mathematics. But some
competences (such as using the connectives AND, OR, proof by contradiction,
understanding of quantifiers “for all” and “there exists”) are partly trained by
other courses and even at secondary school.
• Sets: all competences are target except of:
- compare the algebra of switching circuits to that of set algebra and logical
connectives – missing;
- analyse simple logic circuits comprising AND, OR, NAND, NOR and EXCLUSIVE
OR gates – missing.
The reason is the same: there is a special course “Mathematical logic and
theory of algorithms” that is not a part of Discrete Mathematics in OMSU.

4. OMSU vs EU Curricula study
(focusing on Discrete Mathematics)SEFI study
LEVEL 1
• Mathematical induction and recursion: all competences are target.
• Graphs: all competences are target.
• Combinatorics (Statistics and probability): all competences are target.
Traditionally combinatorics is referred to as a section of Discrete Mathematics
because it is very tightly connected with sets theory.
LEVEL 2
• Number systems:
- carry out arithmetic operations in the binary system – missing;
- carry out arithmetic operations in the hexadecimal system – missing.
These topics are studied at the course of “Informatics” because these systems
are used for information representation in computers.

5. OMSU vs EU Curricula study
(focusing on Discrete Mathematics)SEFI study
LEVEL 2
• Algebraic operations: all competences are target.
• Recursion and difference equations:
- define a sequence by a recursive formula – target;
- all other competences are missing.
• Relations: all competences are target.
• Graphs: all competences are target.
• Algorithms: all competences are target except of:
- understand the notion of an NP problem (as a problem for which It is 'easy' to
verify an affirmative answer) – missing;
- understand the notion of an NP-complete problem (as a hardest problem
among NP problems) – missing.
There is a course “Mathematical logic and theory of algorithms” which is
provided after Discrete Mathematics.

6. OMSU vs EU Curricula study
(focusing on Discrete Mathematics)SEFI study
LEVEL 2
• Geometric spaces and transformations (Geometry).
- understand the group representation of geometric transformations – target.
This competence is for “Group theory section”.
LEVEL 3
• Combinatorics:
- Understanding the link between n-ary relations and relational databases.
Ability to normalize database and to convert from 1NF to 2NF – target.
• Graph theory:
- Write a computer program that finds the components of connectivity,
minimal spanning tree and so on – target.

7. OMSU vs EU Curricula study
(focusing on Discrete Mathematics)SEFI study
LEVEL 3
• Algebraic structures:
- using Shannon-Fano's and Huffman's methods to obtain optimal code –
target;
- knowing LZW zipping algorithm – target;
- knowing Diffie-Hellman key exchange method – target;
- knowing RSA algorithm – target.
These competences are formed if there is a time left for this material.

8. OMSU vs EU Curricula study
(focusing on Discrete Mathematics)Course comparison
OMSU (Russia) TUT (Finland)
Course name Discrete Mathematics Discrete Mathematics
Bachelor / Master Bachelor Bachelor
Preferred year 1 or 2 2
ECTS credits 5 cu = 180 hours (1 cu = 36
hours)
4 cu = 105 hours (1 cu = 27
hours)
Course duration 18 weeks (semester) 7 weeks (learning period, that
is half of a semester)
Number of lessons 36 lecture hours
36 training hours
28 lecture hours
12 training hours

9. OMSU vs EU Curricula study
(focusing on Discrete Mathematics)Course comparison
OMSU (Russia) TUT (Finland)
Course description Set theory. Combinatorics.
Graph theory. Algebraic
structures. Number theory.
Coding theory.
Some functions (floor, ceiling,
sign, Heaviside, etc). The Z-
transform. Number theory.
Graph theory.
Major outcomes Student must know the
notions, understand the
concepts, be able to solve
typical problems and use
algorithms of set theory,
combinatorics, algebra,
number theory and coding
theory.
Unfortunately,
information is missing :-(

10. OMSU vs EU Curricula study
(focusing on Discrete Mathematics)Course comparison
Overall comparison. Courses are quite different:
• OMSU course is much more extensional (180 hours vs 105), but TUT course is
more intensive (7 weeks vs 18).
• In OMSU greater focus is made on training (36 training hours vs 12).
• Course content varies significantly:
- There are two common topics (number theory and graph theory), but in
OMSU greater attention is paid to graph theory and in TUT – to number
theory (as it follows from detailed course description – isn’t depicted here).
- Set theory and combinatorics, algebraic structures and coding theory are
studied in OMSU and aren’t studied in TUT in this particular course.
- The Z-transform is studied in TUT and isn’t studied in OMSU.
Conclusion. It may be said that Discrete Mathematics course in TUT is a
complimentary course for Discrete Mathematics in OMSU.

11. The ideas are not only for Discrete Mathematics, but for other course (AlGeo) as
well. We hope they will be useful for other courses, too.
• Increase the number of engineering examples in the course. For that purpose
mathematicians must have a conversation with engineering courses teachers
and be in a tight contact with them later. UCBL (Lyon) experience –
mathematicians consult with engineering courses upon topics:
- What mathematics is needed for the general purposes of education?
- What amount of mathematics is needed?
- When is it needed (what semester / year of tuition)?
• Using MathBridge:
- (Perhaps, partly) put the lections in MathBridge system.
- Provide homework / tests in MathBridge. This would be helpful according to
OMSU rating system and will free time on trainings (now teacher checks
students’ homework in training classes).
OMSU vs EU Curricula study
(focusing on Discrete Mathematics)Modernization ideas