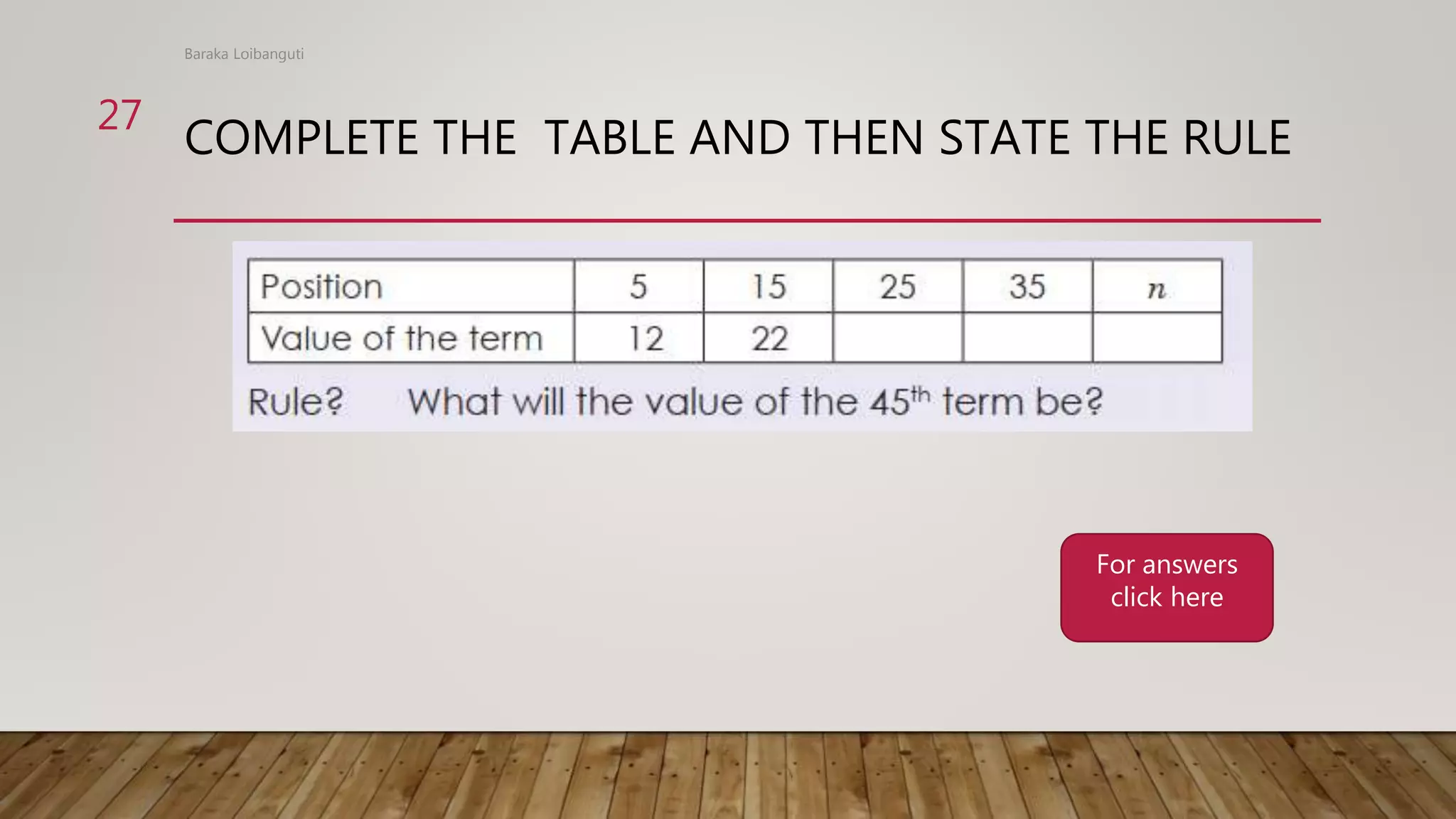
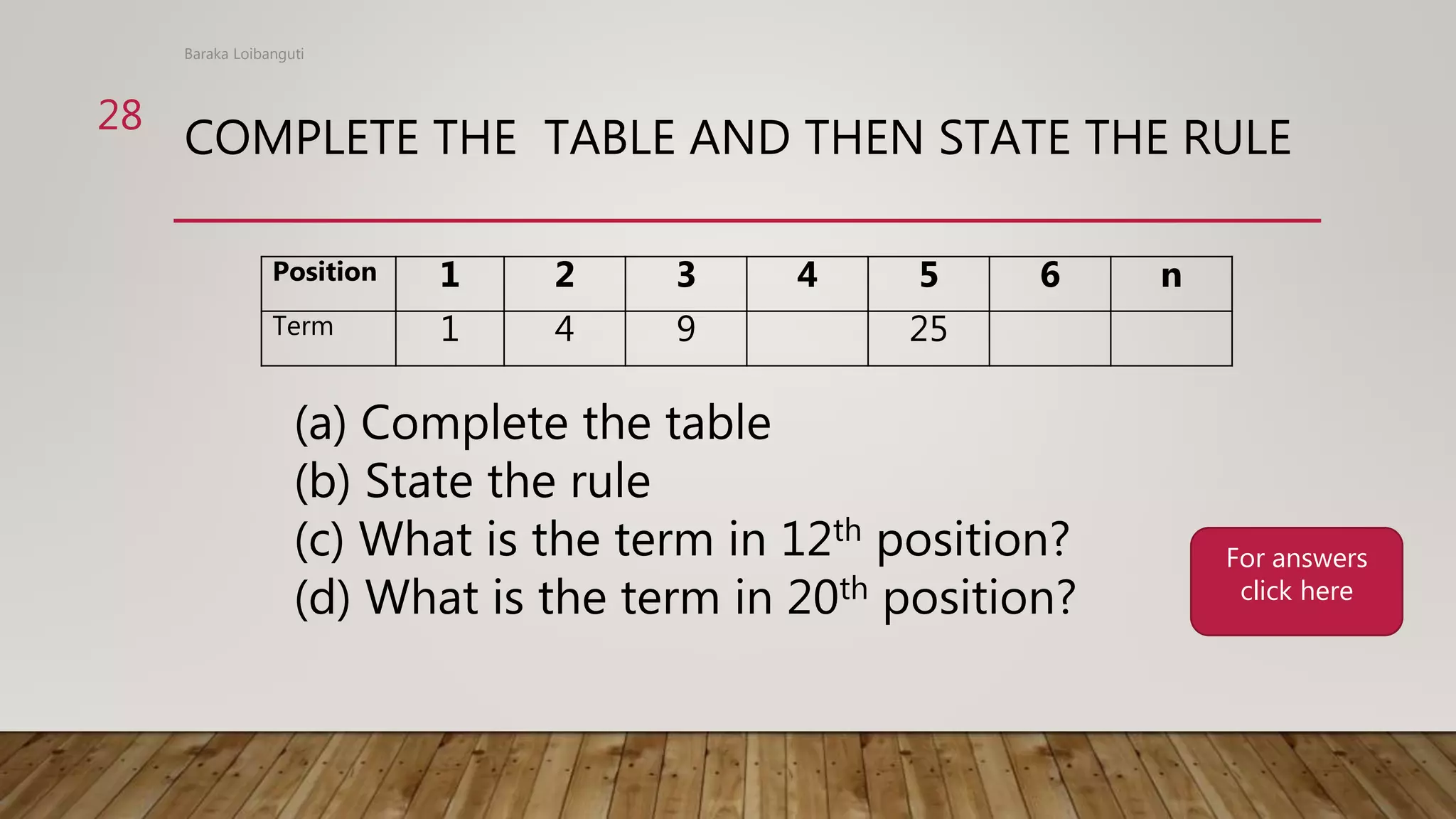
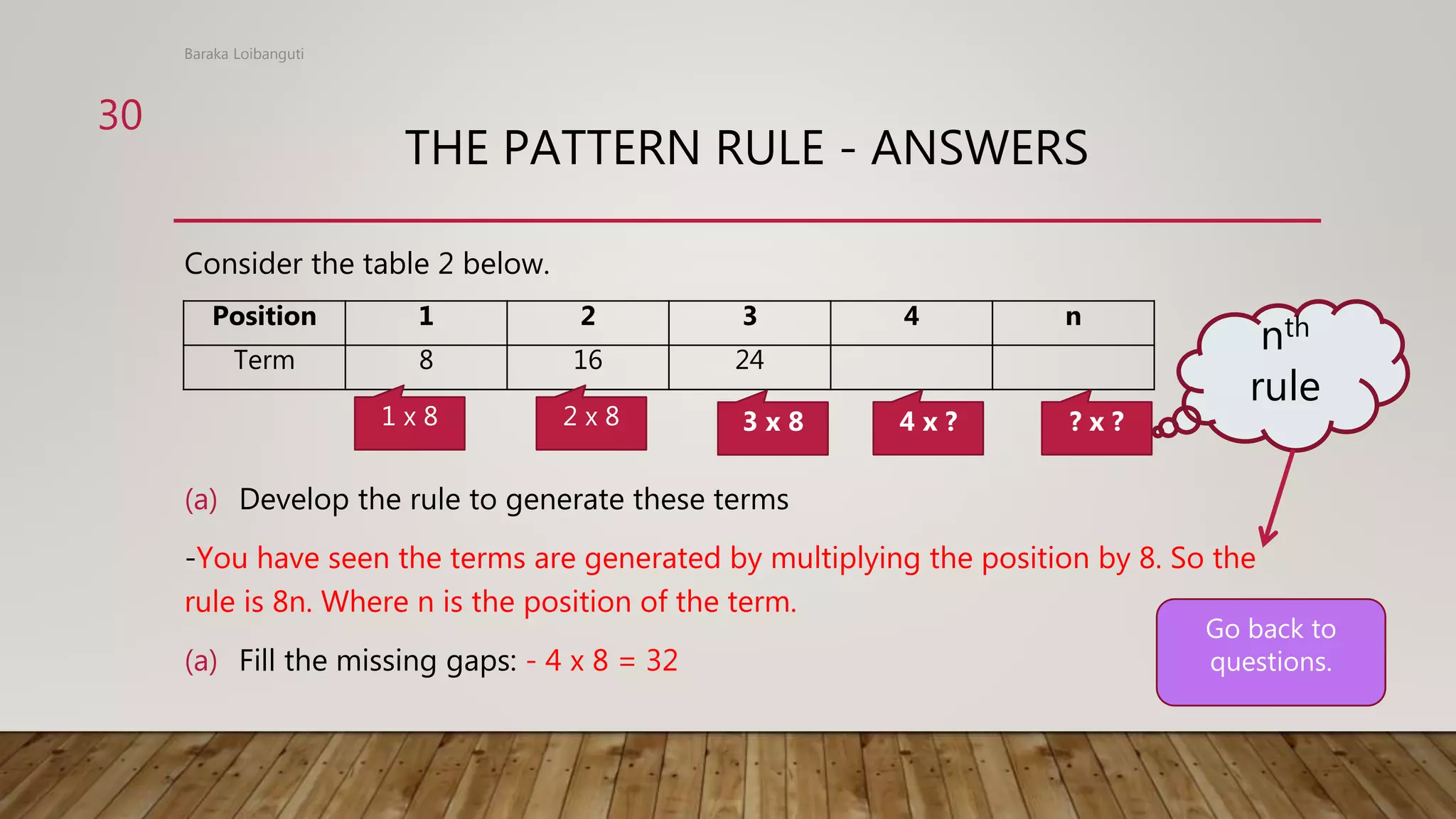
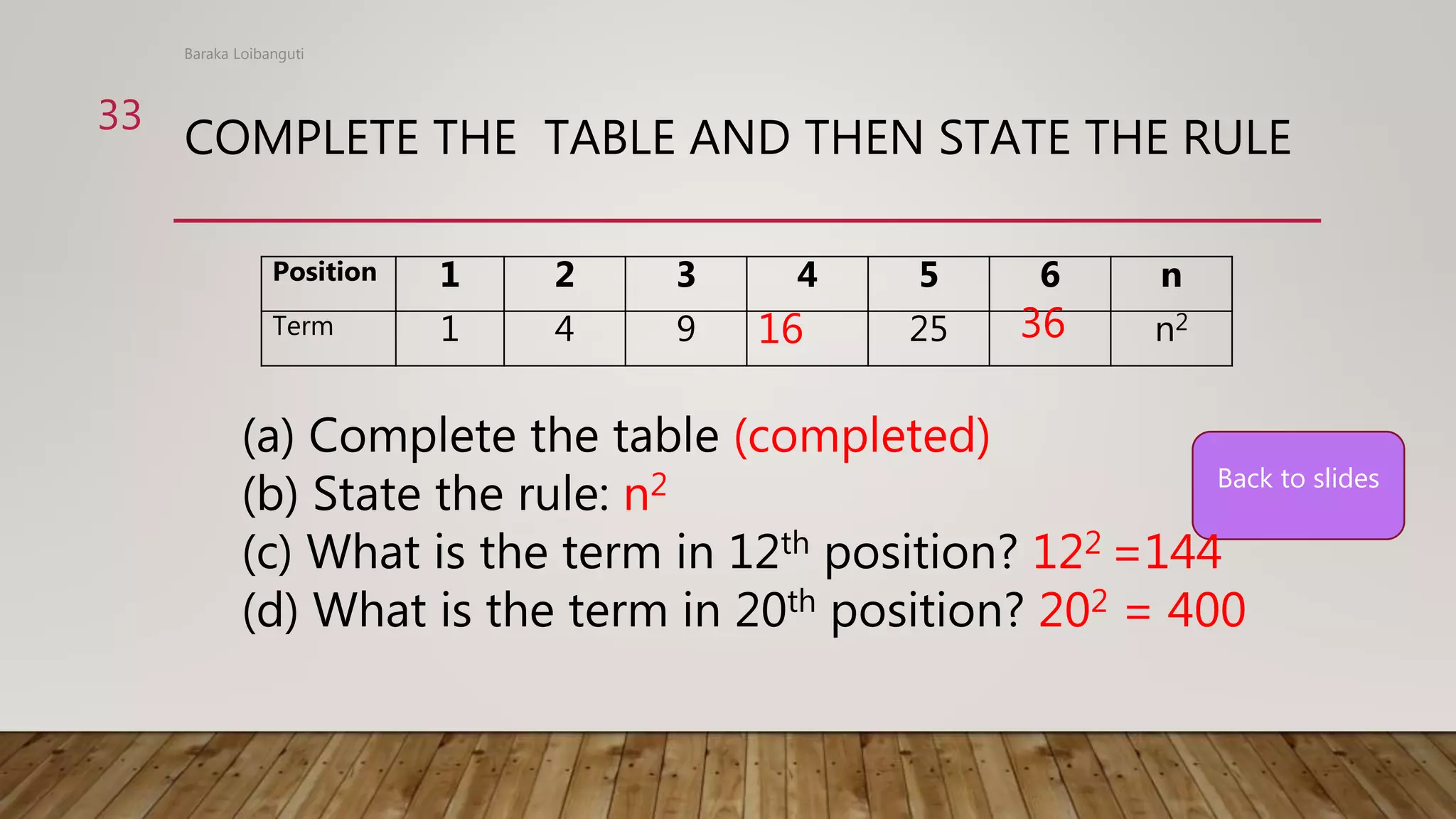
The document discusses numeric patterns, including arithmetic and geometric patterns. Arithmetic patterns have a common difference between consecutive terms, while geometric patterns have a common ratio. Examples are provided of determining the common difference or ratio of patterns and using these to find missing terms or generate additional terms of the pattern. Rules for numeric patterns are also discussed, where the term value is determined by a rule related to the position of the term.

1. NUMERIC PATTERN
GRADE 8
Baraka Loibanguti
1

2. NUMERIC PATTERN
Numeric patterns are commonly divided into
1. Arithmetic (made by adding or subtracting a number each
time).
2. Geometric (which involve multiplying or dividing by a number).
Some geometric patterns are exponential, that is, they are
made by multiplying by an exponent.
Baraka Loibanguti
2

3. ARITHMETIC PATTERNS
The arithmetic patterns are one obtained by adding or
subtracting a constant number all the time. The constant
number is called the common difference.
Example of arithmetic patterns
(a) 2, 4, 6, 8, 10, …,…, …, …, … (can you guess the missing terms?
Baraka Loibanguti
3

4. ARITHMETIC PATTERN CONT.…
From
2, 4, 6, 8, 10, …,…, … The numbers 2, 4, 6, 8, 10 are referred to as
TERMS.
Therefore,
2 is the first term
4 is the second term
6 is the third term
8 is the fourth term
10 is the fifth term etc.
Baraka Loibanguti
4

5. ARITHMETIC PATTERN CONT.…
From
2, 4, 6, 8, 10, …,…, …
The constant difference is obtained by taking the second term minus the first term or
the third minus the second term or fourth minus the third term etc.
The common difference of the pattern above is 2. Thus,
The 2nd term – the 1st term: 4 – 2 = 2 or
The 3rd term – the 2nd term: 6 – 4 = 2 or
The 4th term – the 3rd term: 8 – 6 = 2 etc
Baraka Loibanguti
5

6. ARITHMETIC PATTERN CONT.…
Can you tell the common difference between the terms of the patterns below and
find the next term.
1. 7, 11, 15, 19, 23, 27, … d = _______, the 7th term =_________
2. 5, 13, 21, 29, 37, … d = _______, the 6th term = _________
3. 18, 15, 12, 9, 6, … d = _______, the 6th term =_________
4. 40, 35, 30, 25, … d = _______, the 5th term = _________
Check your
answers
Baraka Loibanguti
6

7. PATTERNS
Which of the following patterns arithmetic?
a) 3, 8, 13, 18, 23, …
b) 11, 17, 23, 29, …
c) 7, 14, 20, 28, 36, …
d) 0, 7, 14, 21, …
e) 48, 43, 40, 31, 27,….
Baraka Loibanguti
Check your
answers
7

8. ARITHMETIC PATTERNS
For each of the arithmetic pattern below find the next TWO terms.
a) 100, 103, 106, 1009, __, __.
b) 200, 189, 178, 167, __, __.
c) 30, 37, 44, 51, __, ___.
d) 50.0, 54.3, 58.6, 62.9, __,__,
e) 2, 8, 14, 20, __, ___,
Baraka Loibanguti
Check your
answers
8

9. ARITHMETIC PATTERNS
The following are arithmetic patterns
Find the missing term
a) 5, 9, ___, 17, 21, ____, 29.
b) ___, ____, 19, 24, 29, 34.
c) 4, ____, 34, 49, 64, ___, 94.
Baraka Loibanguti
9
Check your
answers

10. SUMMARY
We have discussed the arithmetic patterns and you
have noted that THE ARITHMETIC PATTERNS have
the common difference between the consecutive
terms. Using this common difference you can
determine the next few terms of the pattern. [Feel
free to repeat the part for further clarification].
Baraka Loibanguti
10

11. ANSWERS
Baraka Loibanguti
11

12. ARITHMETIC PATTERN ANSWERS
Can you tell the common difference between the terms of the patterns below and
find the next term.
1. 7, 11, 15, 19, 23, 27, … d = _______, the 7th term =_________
2. 5, 13, 21, 29, 37, … d = _______, the 6th term = _________
3. 18, 15, 12, 9, 6, … d = _______, the 6th term =_________
4. 40, 35, 30, 25, … d = _______, the 5th term = _________
4 31
8
-3
-5
45
3
20
Baraka Loibanguti
12
Go back to
questions?

13. PATTERNS ANSWERS
• Which of the following patterns arithmetic?
a) 3, 8, 13, 18, 23, … it is arithmetic
b) 11, 17, 23, 29, … it is arithmetic
c) 7, 14, 20, 28, 36, … it is not arithmetic
d) 0, 7, 14, 21, … it is arithmetic
e) 48, 43, 40, 31, 27,…. it is not arithmetic
Baraka Loibanguti
13
Go back to
questions?

14. ARITHMETIC PATTERNS ANSWERS
For each of the arithmetic pattern below find the next TWO terms.
a) 100, 103, 106, 1009, 112, 115
b) 200, 189, 178, 167, 156, 145
c) 30, 37, 44, 51, 58, 65
d) 50.0, 54.3, 58.6, 62.9, 67.2,71.5
e) 2, 8, 14, 20, 26, 32
Baraka Loibanguti
14
Go back to
questions?

15. ARITHMETIC PATTERNS ANSWERS
The following are arithmetic patterns
Find the missing term
a) 5, 9, 13, 17, 21, 25, 29.
b) 9, 14, 19, 24, 29, 34.
c) 4, 19, 34, 49, 64, 79, 94.
Baraka Loibanguti
15
Go back to
questions?

16. Baraka Loibanguti
16

17. GEOMETRY PATTERN
Geometric patterns are obtained when multiplying or
dividing by a constant term all the time. The common
constant is called common ratio, r.
To get the common ratio is obtained by:-
r=
second term
first term
=
third term
second term
=
fourth term
third term
Baraka Loibanguti
17

18. EXAMPLE
Determine the common ratio of the following geometric
patterns
3, 9, 27, 81, 243, …
Ratio, r =
2nd term
1st term
=
3rd term
2nd term
=
4th term
3rd term
=
5𝑡ℎ
term
4th term
Ratio, r = 9 ÷ 3 = 27 ÷ 9=81 ÷ 27 = 243 ÷ 81 = 3
Baraka Loibanguti
18

19. Determine the ratio of the following patterns
a) 1, 4, 16, 64, 128, …
b) 2, 4, 8, 16, 32, …
c) 81, 27, 9, 3, 1, …
d) -7, -14, -28, -56, …
e) 9, 6, 4, …
Baraka Loibanguti
19
Click here
for Answers

20. Determine the next term of the following geometric
patterns
a) 7, 21, 63, 189, ___.
b) 4, 16, 64, 256, ___.
c) 6, 12, 24, 48, ___.
d) 8, 40, 200, ___.
e) 1, 7, 49, 343, ___.
Baraka Loibanguti
20
Click here
for Answers

21. Determine the ratio of the following patterns
a) 1, 4, 16, 64, 128, … r = 4
b) 2, 4, 8, 16, 32, … r = 2
c) 81, 27, 9, 3, 1, … r = 1/3
d) -7, -14, -28, -56, … r = 2
e) 9, 6, 4, … r = 2/3
Baraka Loibanguti
21
Back to
slides?
Click here

22. Determine the next term of the following geometric
patterns
a) 7, 21, 63, 189, 567.
b) 4, 16, 64, 256, 1024.
c) 6, 12, 24, 48, 96.
d) 8, 40, 200, 1000.
e) 1, 7, 49, 343, 2401.
Baraka Loibanguti
22
Click
me!

23. Baraka Loibanguti
23

24. THE PATTERN RULE
Consider the table 1 below
Baraka Loibanguti
24
Position 1 2 3 4 5 n 25
Term 3 6 9 12 15 3 x n ?
The rule: The position of the term x 3 = n x 3
What is the missing value?
= 25 x 3 = 75

25. THE PATTERN RULE CONT…
Consider the table 2 below.
(a) Develop the rule to generate these terms
(b) Fill the missing term
Baraka Loibanguti
25
Position 1 2 3 4 n
Term 8 16 24
Check your
answers

26. THE PATTERN RULE CONT…
Consider the table 3 below.
(a) Develop the rule to generate these terms
(b) Fill the missing gaps
(c) What is the term in 20th position?
Baraka Loibanguti
26
Position 1 2 3 4 5 n
Term 6 7 8 9
Check your
answers

27. COMPLETE THE TABLE AND THEN STATE THE RULE
Baraka Loibanguti
27
For answers
click here

28. COMPLETE THE TABLE AND THEN STATE THE RULE
Baraka Loibanguti
28
For answers
click here
Position 1 2 3 4 5 6 n
Term 1 4 9 25
(a) Complete the table
(b) State the rule
(c) What is the term in 12th position?
(d) What is the term in 20th position?

29. SUMMARY
• Geometric patterns have the common ratio
• To get the next term, take the previous term times the ratio
• The pattern rule depends on position of the term
• Generate the terms using the rule developed from the patterns
Baraka Loibanguti
29

30. THE PATTERN RULE - ANSWERS
Consider the table 2 below.
(a) Develop the rule to generate these terms
-You have seen the terms are generated by multiplying the position by 8. So the
rule is 8n. Where n is the position of the term.
(a) Fill the missing gaps: - 4 x 8 = 32
Baraka Loibanguti
30
Position 1 2 3 4 n
Term 8 16 24
Go back to
questions.
1 x 8 2 x 8 3 x 8 4 x ? ? x ?
nth
rule

31. THE PATTERN RULE CONT…
Consider the table 3 below.
(a) Develop the rule to generate these terms
- You have seen that the terms are generated by adding 5 to the
term’s position. The rule is 5 + n
(a) Fill the missing term: = 5 + 5 = 10
(b)In 20th position the term is 20+5=25
Baraka Loibanguti
31
Position 1 2 3 4 5 n
Term 6 7 8 9
Go back to
slides

32. COMPLETE THE TABLE AND THEN STATE THE RULE
Baraka Loibanguti
32
Back to slides
 The table is filled
 The rule is 7 + position; thus 7 + n
32 42 7 + n

33. COMPLETE THE TABLE AND THEN STATE THE RULE
Baraka Loibanguti
33
Back to slides
Position 1 2 3 4 5 6 n
Term 1 4 9 25 n2
(a) Complete the table (completed)
(b) State the rule: n2
(c) What is the term in 12th position? 122 =144
(d) What is the term in 20th position? 202 = 400
16 36

34. • May I here from you?
-How did you find these slides?
-Anything to be improved?
-Let me know by clicking the safe link below
Baraka Loibanguti
34
barakaloibanguti@gmail.com