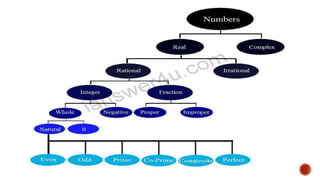
This document discusses key concepts in number theory, including: - Divisibility, prime numbers, composite numbers, greatest common factor, and the division algorithm. - A number is divisible by another if the second number is a factor of the first. Prime numbers are only divisible by 1 and themselves, while composite numbers are divisible by other numbers besides 1 and themselves. - The greatest common factor is the largest integer that divides two numbers. For example, the greatest common factor of 24 and 36 is 12.

2. Dr. Zafar Iqbal Khan

3. Number Theory or Theory of Numbers is a part of
DISCRETE MATHEMATICS
about integers and their properties.

5. Number Theory deals with the study of the properties of this set of
numbers ({1,2,3,4…}) and the key concept to this theory is….
Divisibility
Prime Numbers
Composite Numbers
Greatest Common Factor
The Division Algorithm

6. The natural number a is divisible by the natural number
b such that…….
a = b k
b|a
“|” symbols denotes “Divides”

7. If “b” divides “a” then…..
o b | a ______ True
o a | b _____ False
If “b” does not divide “a” then......
b X a

8. 1. 77|7
2. 7|77
3. 24|24
4. 0|24
5. 24|0

9. 1. 77|7 : true bigger number can divide smaller
positive number
2. 7|77 : false
3. 24|24 : true because 24=24.1
4. 0|24 : only 0 is divisible by 0
5. 24|0 : true , 0 , is divisible by every number
(0=24.0 )

10. Definition:
A number n≥2 prime if it is divisible by 1 and itself.
2,3,5,7………
A number n ≥2 which is not prime is called composite
numbers.
4,6,8,9……..

11.  0 & 1
 4 & 8
 3 & 7

12. 0 & 1 ( not prime because not satisfying the
condition n ≥2 )
4 & 8 ( not prime numbers because they are
divisible by 2 ,and itself )
3 & 7 ( prime because they are divisible
by itself )
It is to be noted that all odd numbers are
not prime because 9 is odd and it is not prime

13. Theorem:
Every positive can be written uniquely as a product of primes ,
where the prime factor are written in order of increasing size.
“Any number n ≥2 can be expressible as a unique product of 1 or more
prime numbers”

14. a) 15 = 3.5
b) 48 = 2.2.2.2.3
c) 100 = 2.2.5.5
d) 512 = 2.2.2.2.2.2.2.2.2
e) 515 = 5.103

15. “The largest integer that
divides both of two integers is
called greatest common divisor of these integers”

16. What is the greatest common divisor of 24 and 36 ?
Answer:
The positive common divisors of 24 & 36 are 1,2,3,4,6 &12.
Hence ….
gcd(24,36) = 12

17. What is the greatest common divisor of 17 and 22 ?
Answer:
 The integers 22 &17 have no positive common divisors other than 1.
Hence ….
gcd(17,22) = 1

18. Let a be an positive integer and d be a positive number.
Then there are some unique integer q and r ,with
Such that…..
a = dq + r
where….
d is called divisor.
a is called the dividend.
q is called quotient.
r is called remainder.

19. When we divide 17 by 5 then …
17= 5.3+2
17 is the dividend.
5 is the divisor.
3 is called the quotient.
2 is called the remainder.

20. Thankyou