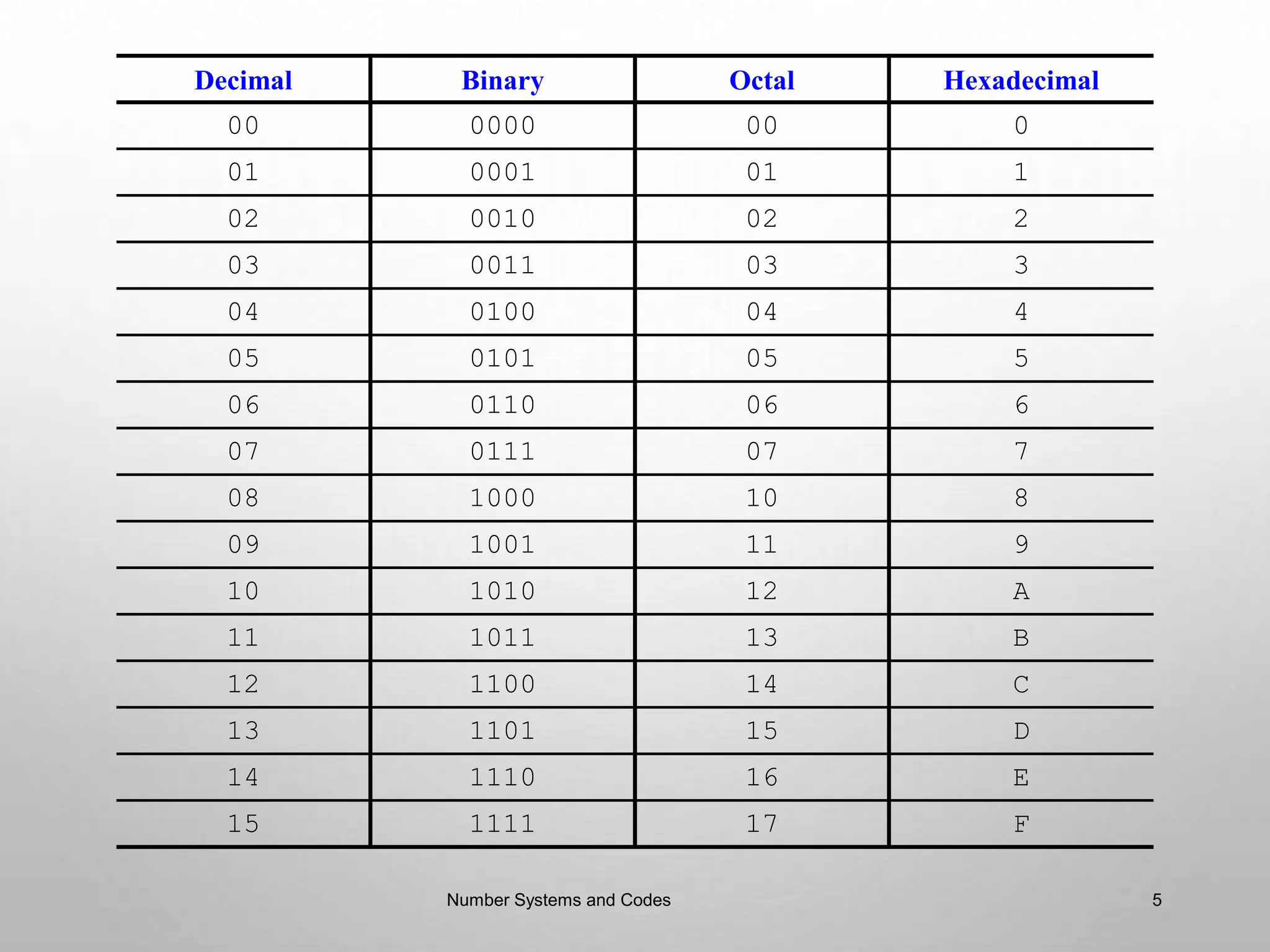
This document provides an overview of number systems and codes. It discusses the decimal, binary, octal, and hexadecimal number systems. It covers topics like number notation, arithmetic operations, base conversions, and signed number representation using signed-magnitude, 1's complement, and 2's complement methods. Codes like decimal codes, Gray code, and ASCII code are also briefly mentioned.