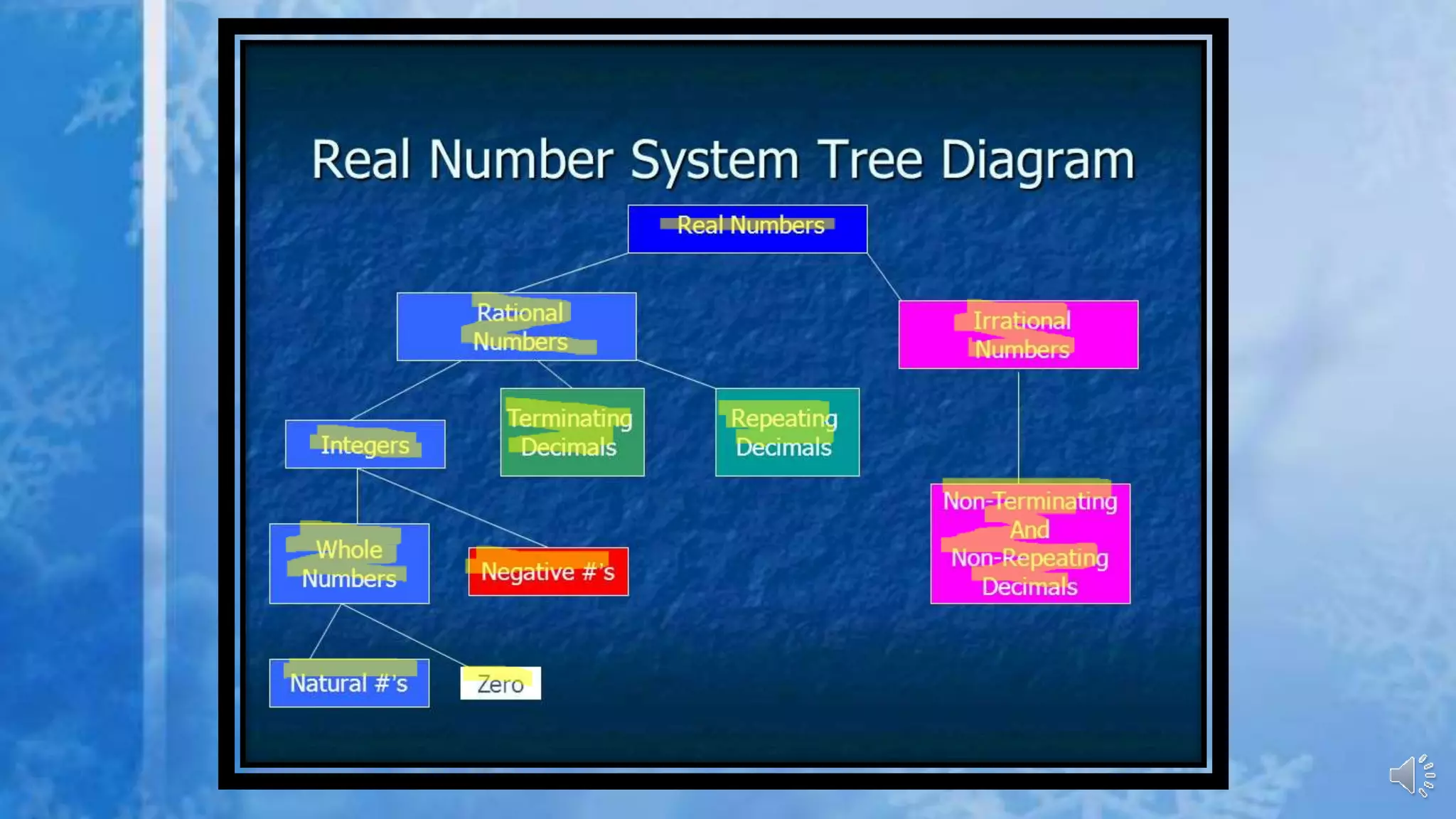
The document explains different types of number systems including natural numbers, whole numbers, integers, and rational numbers. It highlights how rational numbers can be expressed as fractions and provides methods for converting decimals into rational numbers. Additionally, it categorizes decimal representations into terminating and recurring types based on their denominators.

1. NUMBER systems
CHAPTER1

2. TYPE OF NUMBERS
Natural numbers (N): the counting numbers
1,2,3…….
Whole numbers (W): Zero along with all natural
numbers 0,1,2,3….
Integers (Z): Negative and positive numbers along
with zero
…..-3,-2,-1,0,1,2,3…..
Rational numbers (Q): All integers, fractions and
decimal numbers
0.25, -17,
𝟏
𝟓
,
𝟏𝟑
𝟕
,
−𝟐
𝟏𝟏

3. RATIONAL NUMBERS
Any number that can be written in the form
𝒑
𝒒
, integers , q ≠ 0.
p and q have no common factors other than 1
(that is, p and q are co-prime)
Do you think a
natural number is
a rational ?
Yes, 3 can be
written as
3
1
Do you think a 2.5
is a rational ?
Yes, 2.5 can be
written as
25
10
=
5
2

4. NUMBERSYSTEM

5. Decimal representation of rational numbers
𝟕
𝟏𝟎
= 0.7
𝟓
𝟐
= 2.5
𝟕
𝟒
= 1.75
Note:
remainder
is zero

6. Decimal representation of rational numbers
𝟐
𝟑
= 0.666….
= 0. 𝟔
𝟏
𝟕
= 0.142857142857….
= 0.𝟏𝟒𝟐𝟖𝟓𝟕
𝟏
𝟔
= 0.166666…
=0.1 𝟔
Note:
remainder
is never
zero

7. AmI a terminatingorrecurringdecimal???
›
𝟑𝟕
𝟐𝟓𝟎
If denominator has factors 2
and 5 only then is terminating
decimal
Otherwise recurring decimal
or non terminating decimal
37
175
=
37
2×3×5×5
= 0.24666…
=0.24 𝟔
This is recurring
decimal.

8. REPRESENTATION ON NUMBERLINE
1
2 1.7

10. FINDINGRATIONALNUMBERS BETWEENTWO RATIONAL
NUMBERS

11. CONVERTING DECIMALS TO RATIONAL NUMBERS
0.3 =
3
10
0.75 =
75
100
=
3
4
BUT WHAT IF WE NEED TO CONVERT
0.3333….
1.2727….
0.2353535….. into
𝑝
𝑞
form.

12. CONVERTING DECIMALS TO RATIONAL NUMBERS
let x = 0.3333... (i)
Now here is where the trick comes in.
Multiply (i) by 10
 10 x = 10 × (0.333...) = 3.333...
Now, 3.3333... = 3 + x, since x = 0.3333...
Therefore, 10 x = 3 + x
Solving for x, we get
9x = 3,
i.e., x =
𝟏
𝟑

13. CONVERTING DECIMALS TO RATIONAL NUMBERS
Let x = 1.272727...
Since two digits are repeating, we multiply x by
100
 100 x = 127.2727...
So, 100 x = 126 + 1.272727...
100x = 126 + x
Therefore, 100 x – x = 126,
 i.e., 99 x = 126
., x =
𝟏𝟐𝟔
𝟗𝟗
=
𝟏𝟒
𝟏𝟏

14. CONVERTING DECIMALS TO RATIONAL NUMBERS
Let x = 0. 23535….
Over here, note that 2 does not repeat, but the block 35
repeats.
 Since two digits are repeating, we multiply x by 100 to get
100 x = 23.53535...
So, 100 x = 23.3 + 0.23535...
100x = 23.3 + x
Therefore, 99 x = 23.3
i.e., 99 x =
𝟐𝟑𝟑
𝟏𝟎
, which gives
x =
𝟐𝟑𝟑
𝟗𝟗𝟎

15. NCERT QUESTIONEX.1.3 (Q.2)