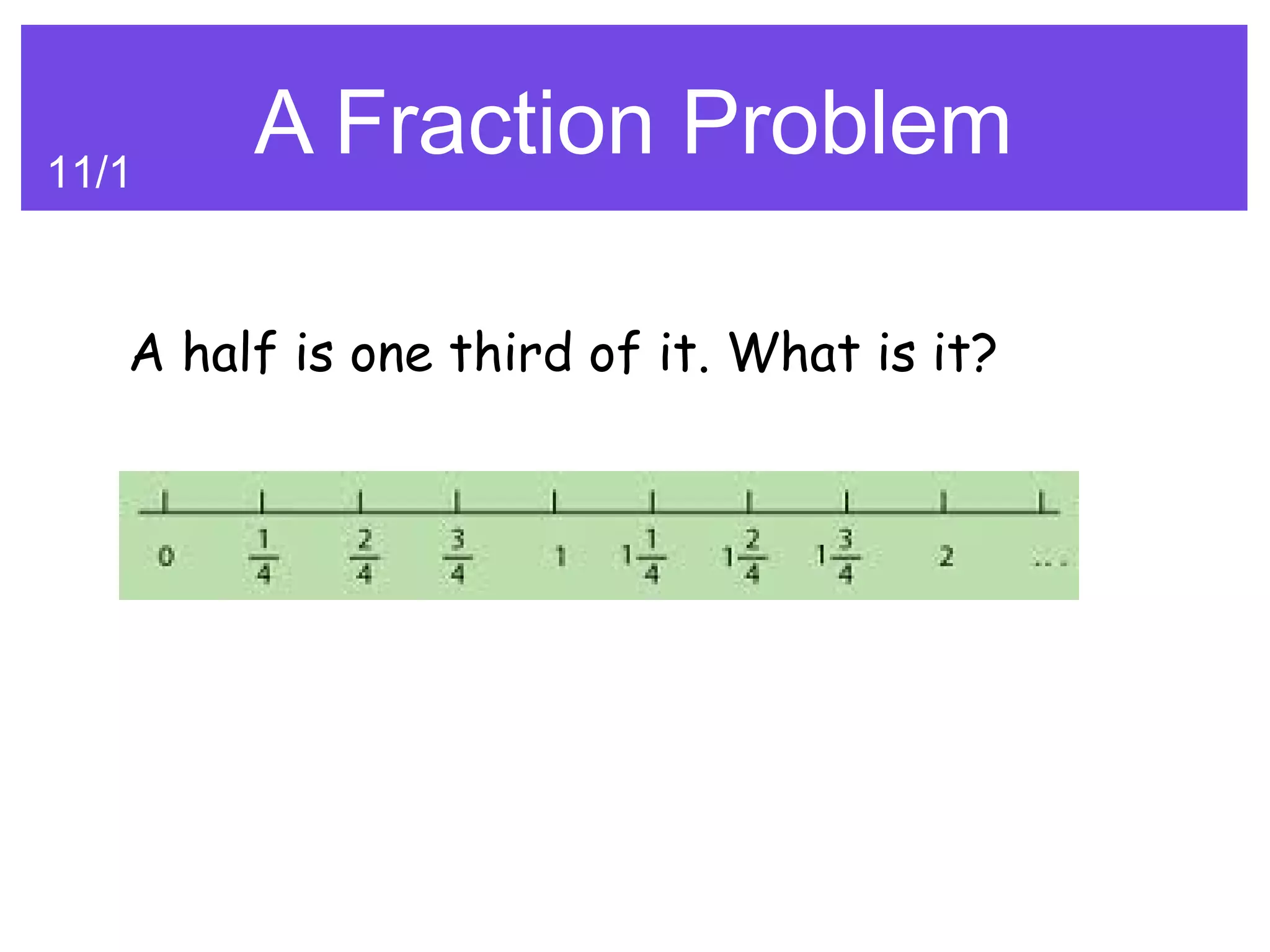
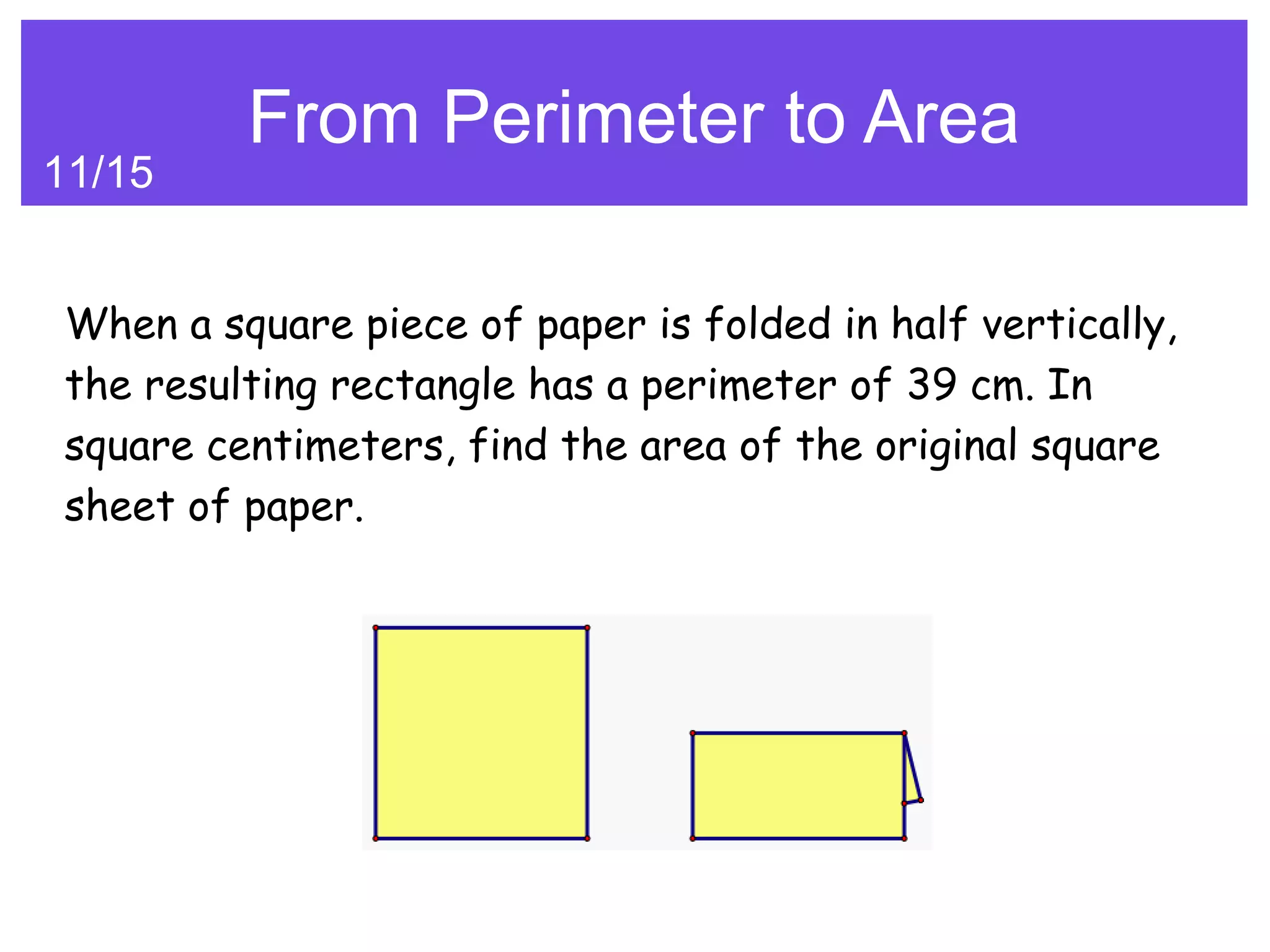
The document outlines a series of mathematical problems, ranging from fractions and prime numbers to logic puzzles and maximum regions with lines through a circle. Each problem has a specific focus or theme, such as finding discounts, calculating pill duration, or determining weights based on group dynamics. The problems involve various mathematical concepts which target critical thinking and problem-solving skills.

1. Problem Solving
MP3: Construct viable arguments and critique the
reasoning of others.

2. 11/1
A Fraction Problem
A half is one third of it. What is it?

3. 11/2
Number of Numbers
How many different 1-, 2-, or 3-digit whole numbers
can be made using the digits 2, 5, and 8?
No digit may be repeated within any one number.
2 5 8

4. 11/5
Fractions and the Flu
You catch the flu, and your
doctor prescribes some
medicine. You are to take one
pill every 2/3 hour. You have
18 pills to take. How many
hours will the pills last?

5. 11/6
Percent Problems
You are going to a sporting goods store to buy
a pair of tennis shoes and a pair of in-line
skates. The original cost of the tennis shoes
was $150, but today that pair of tennis shoes
is 40% off. The original price of the in-line
skates was $200, but today that item is 20%
off. What was the percent of discount on the
total purchase (assuming no taxes are
involved)?

6. 11/7
Twin Primes
Twin primes are a pair of prime numbers such that the lesser
prime number subtracted from the greater prime number is 2.
There are three pairs of twin primes between 100 and 150.
How many pairs of twin primes are there less than 100?
..., 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, ...

7. 11/8
Product of Primes
The product of three prime numbers that are
less than 30 is 1955.
What are the three prime numbers?

8. 11/9
Mystery Number
I am thinking of a special four-digit number:
• All the digits are different.
• The digit in the thousands place is 3 times
the digit in the tens place.
• The number is odd.
• The sum of the digits is 27.
What’s my special four-digit number?

9. 11/13
The Winner is...
The winner of a school election is announced after
school at 4:00 p.m. One student calls 2 friends
before 4:15 p.m., telling the name of the winner.
Before 4:30 p.m., those 2 people call 2 more students
and tell them the name of the winner. Before 4:45
p.m., each new student who has been notified calls 2
more people, telling them the name of the winner. If
this continues and no student is called twice, at what
time will 200 students know the name of the winner?

10. The Product is Prime?
11/14
Find three integers in arithmetic progression (with
equal differences between each number) whose
product is a prime number. (This is possible.)

11. From Perimeter to Area
11/15
When a square piece of paper is folded in half vertically,
the resulting rectangle has a perimeter of 39 cm. In
square centimeters, find the area of the original square
sheet of paper.

12. The Missing Number
11/16
Determine the missing number based on the values in
each square.

13. Hens and Eggs
11/19
If 3 hens lay 4 eggs in 5 days, how
many days will it take a dozen hens to
lay 8 dozen eggs? Please round your
answers to the nearest day (or egg, if
needed).

14. Hug a Tree
11/20
Several years ago, I planted a 3-foot
tree that has grown the same amount
each year. At the end of the third year,
the tree was 1/5 taller than it was at the
end of the second year. The tree is now
18 feet tall. How many years ago did I
plant the tree?

15. Maximize the Regions
11/21
What is the greatest number of
regions you can get if you draw
four straight lines through a
circle? Convince someone that
you found the greatest number!

16. 1, 2, 3,...
11/26
What three consecutive counting
numbers have a sum that is 20% of
the product of the three numbers?

17. Alphanumeric Puzzle
11/27
Find the digits that represent the
letters E, F, G, and H to satisfy the
following puzzle. Each letter
represents a different digit.

18. There’s Algebra in There!
11/28
Complete the table by determining
the value of each letter. Explain
what rule is used to relate the
numbers in the second column
(with the heading of y) with those
in the first column (with the
heading of x).

19. Determining Weights
11/29
Three boys, Jamal, Hector, and Simon, work together on a
farm. They walk into the barn, notice a scale. used to weigh
cattle, and decide to weigh themselves. Unfortunately, the
scale begins at 100 kg and none of the boys weighs more
than 100 kg. They decide to weigh themselves in pairs and
found these amounts. Jamal was sure that he weighed the
most. What did each boy weigh?

20. Mystery Number Puzzle
11/30
Find an integer between 100 and 200 such that each
digit is odd and the sum of the cubes of the digits is
equal to the original three-digit number.