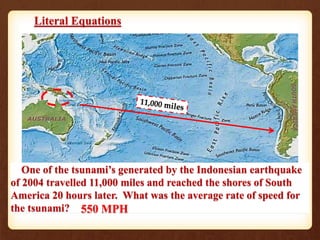
The document provides class notes and examples for solving literal equations. It includes tips for solving different types of literal equations such as distributing terms, clearing fractions, and factoring common terms. Students are given examples such as solving equations for variables like x, y, k, and p. The document also provides an example of calculating average rate of speed using values from a 2004 tsunami.

1. Today:November 17, 2015
 Khan Academy Topic
 Literal Equations
 CW 2.3

2. You can:
a. Add/Subtract the first two fractions,
then add/subtract the third. Or,
b. Find a common denominator, then
simply add/subtract the numerators.
𝟕
𝟖
-
𝟐
𝟖
-
𝟒
𝟖
=

3. What’s the LCD?
The answer is...
𝟏𝟏
𝟏𝟖

4. Using the Distributive Property When Multiplying Fractions
Change to improper fraction
4 x 𝟒
𝟐
𝟗 = 16 +
𝟖
𝟗
= 16
𝟖
𝟗
-3 ÷
𝟕
𝟏𝟔

5. w=
𝟏𝟐𝒔
𝒄
x= −𝟐𝟖
Warm-Up:
d = 2Q - c

6. Class Notes:
Tips for Solving Literal & Other Equations:
1. If the variable you are solving for is inside the
parenthesis, you must distribute first. 9p = 3(k + 5) for k
2. If the variable you are solving for is outside the
parenthesis, simply perform the opposite operation.
9 = k(p + 5) for k
3. When clearing fractions, if the denominator being
multiplied has two or more terms, it must be distributed on
the other side.
5k(2p + 4) = 9
𝟓𝒌
𝟑
=
𝟑
𝟐𝒑+𝟒
for p
Literal Equations:
We need to separate the ‘k’ from the 5 in this case.
Solve the equation.

7. Class Notes:
4. Always check to see if every term has something in
common. You can then factor the common part out.
3kp – 7km – 9k – 1 = -7p + 10 for k
first
3kp – 7km – 9k = -7p + 11 Then,
k(3p – 7m – 9) = -7p + 11 Now What?
k= -7p + 11
(3p – 7m – 9)
Factoring:

8. Tips for Solving Literal & Other Equations:
5. If an entire term can be factored out, replace it
inside the parenthesis with a ‘1’
2p + 8px = ? 2p(1 + 4x) check by distributing the 2p again.
6. When solving fractional equations, you may have to
clear fractions more than once.
4 – 2x =
𝟏
𝟓
𝟔 − 𝟑𝒙
𝟑
20 – 10x = 𝟔 − 𝟑𝒙
𝟑
Complete the first step. Next we clear the....
Solve for x.

10. Class Work 2.3:
Due Thursday, November 19th.
P.S.
Class Work is only credited when submitted
with work showing.
14. Solve for x: y – 2x =
𝒚 −𝟑𝒙
𝟐
Changes to CW 2.3:
Solve for P: D =
𝟏𝟏
𝟓
(P – 3)15.

11. Literal Equations
Solve for y: 3y – 2(x + 1) = y + 3(x + 6)
Find the base of a triangle with an area of
49 in. and a height of 14 in.A = 49
b
14
One of the tsunami’s generated by the Indonesian earthquake
of 2004 travelled 11,000 miles and reached the shores of South
America 20 hours later. What was the average rate of speed for
the tsunami? 550 MPH