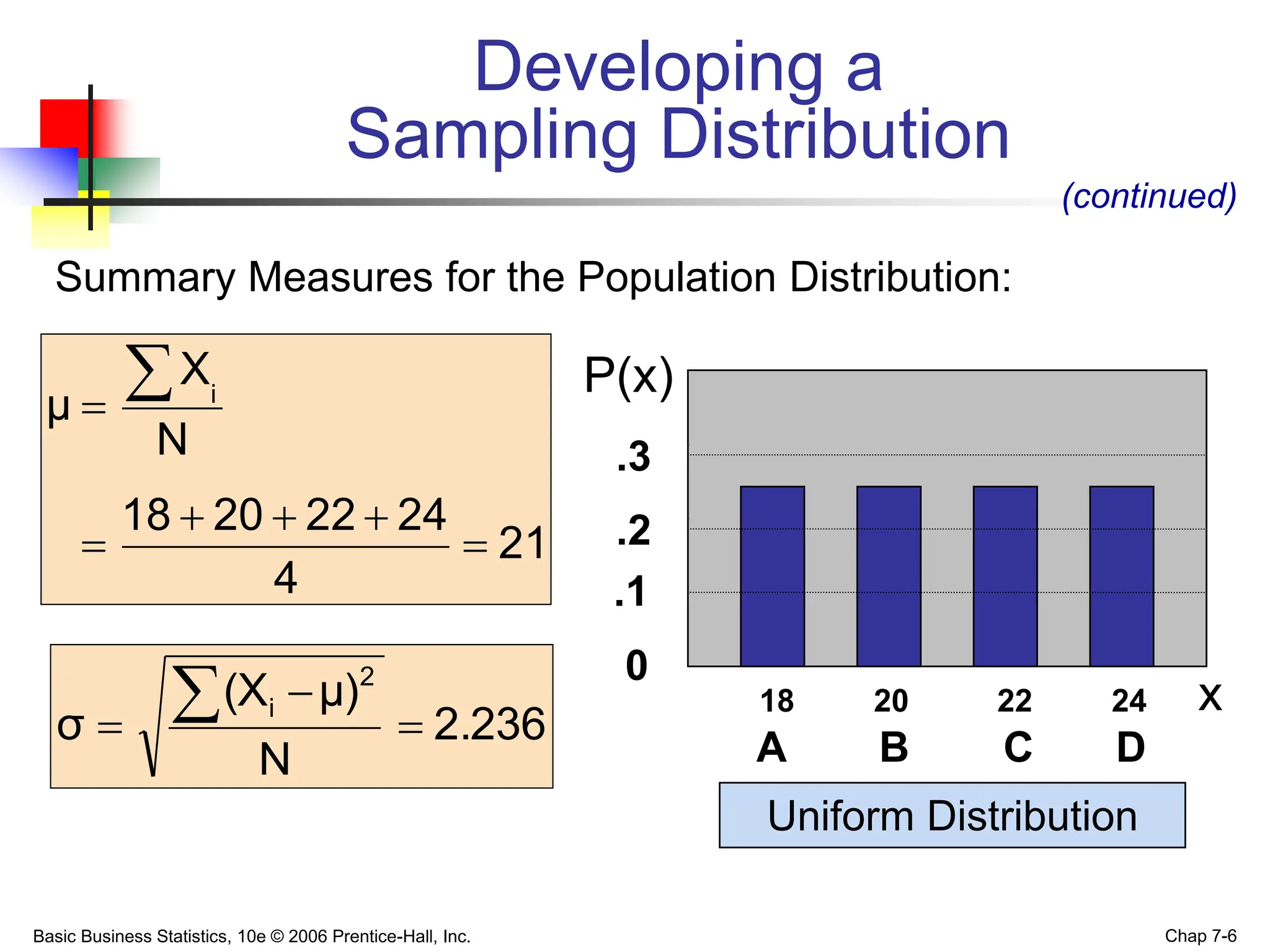
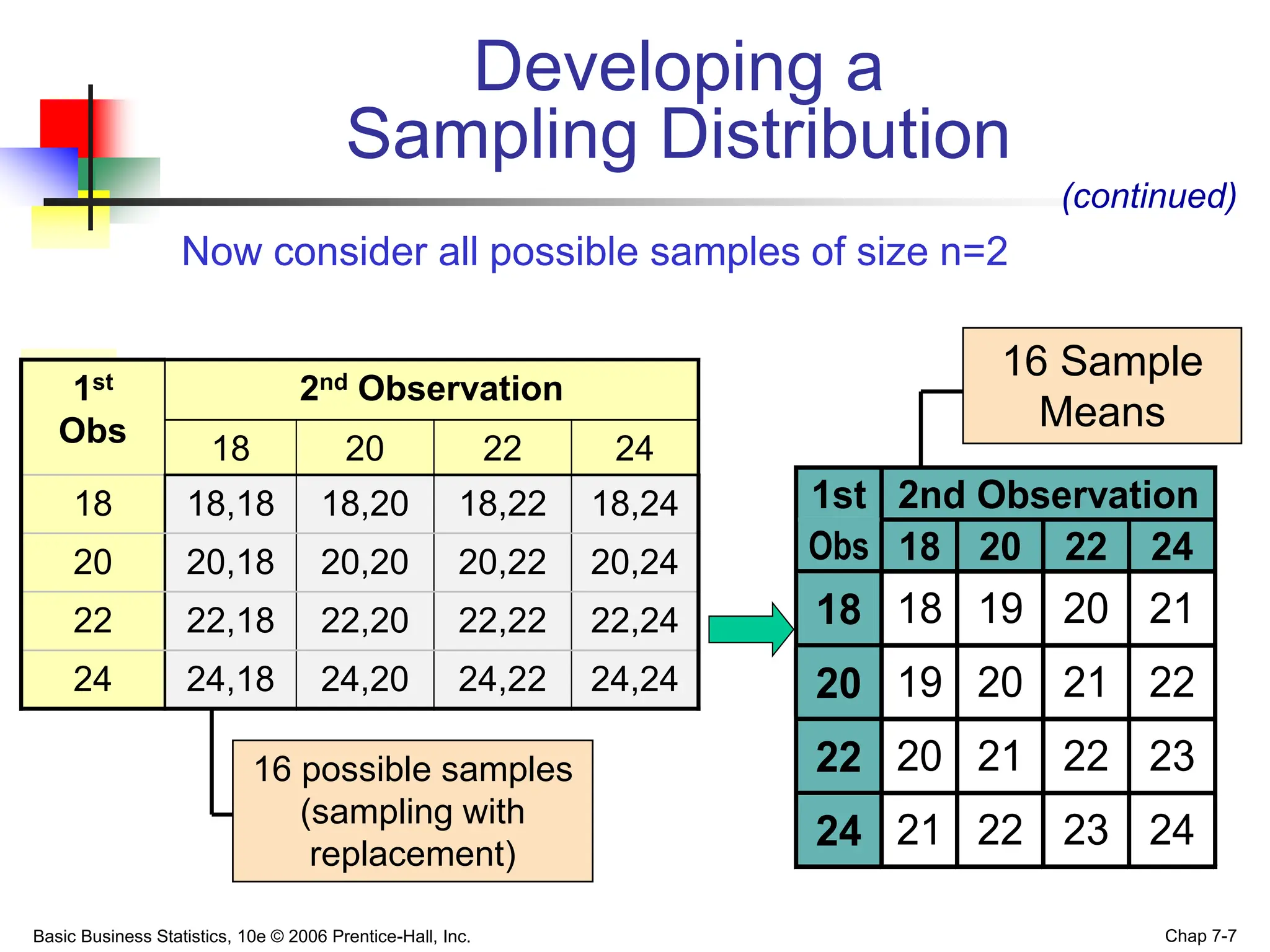
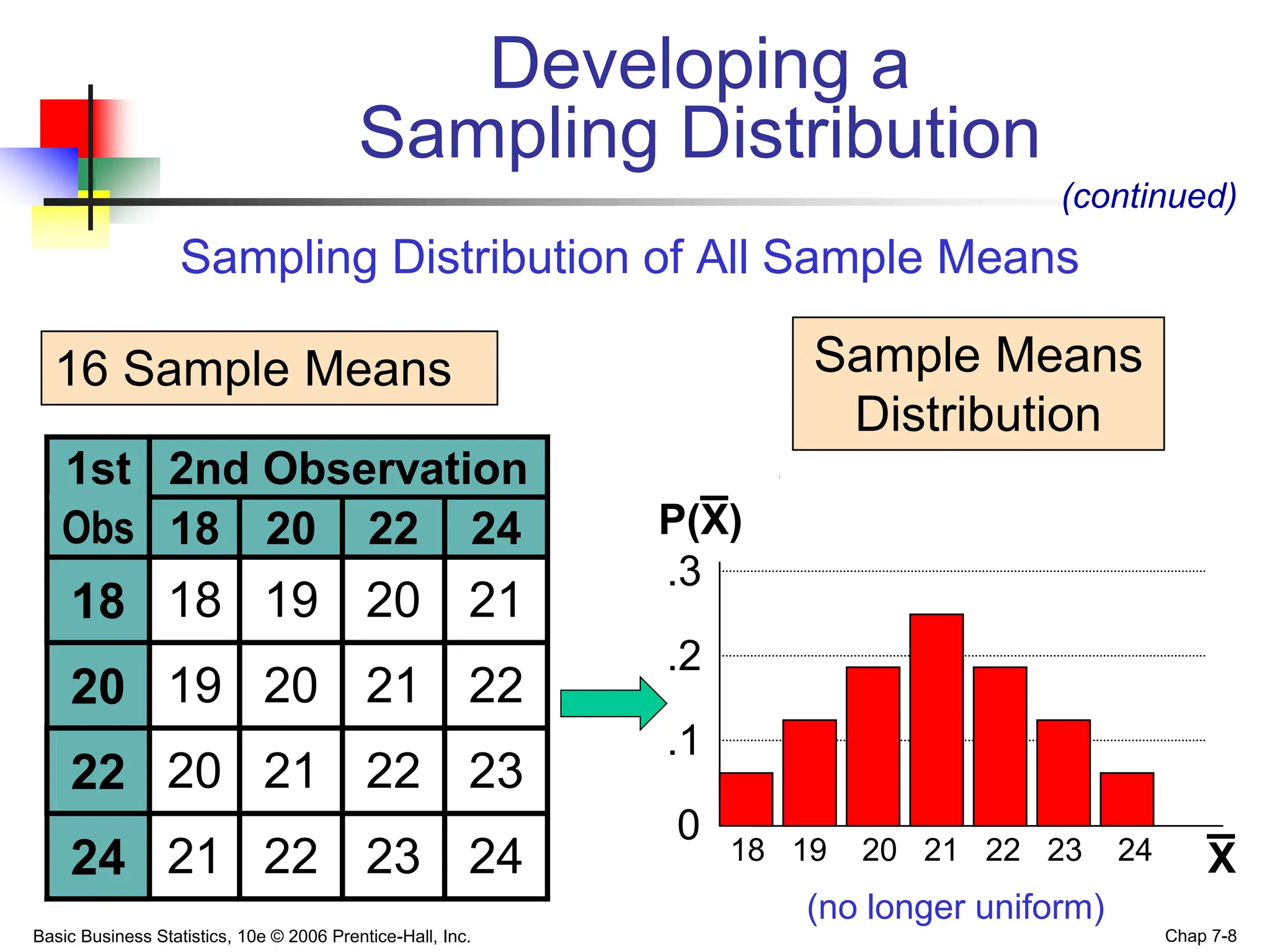
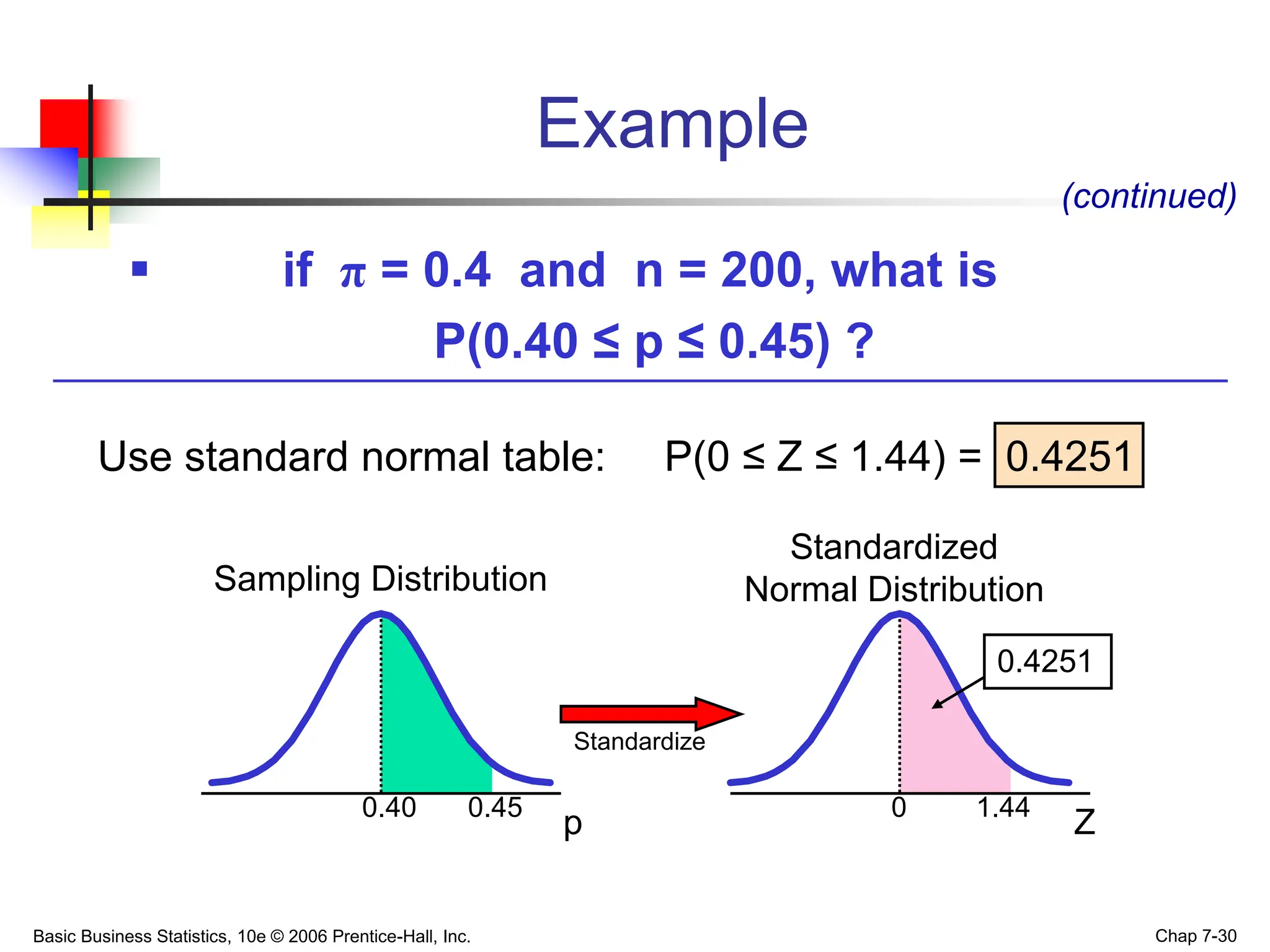
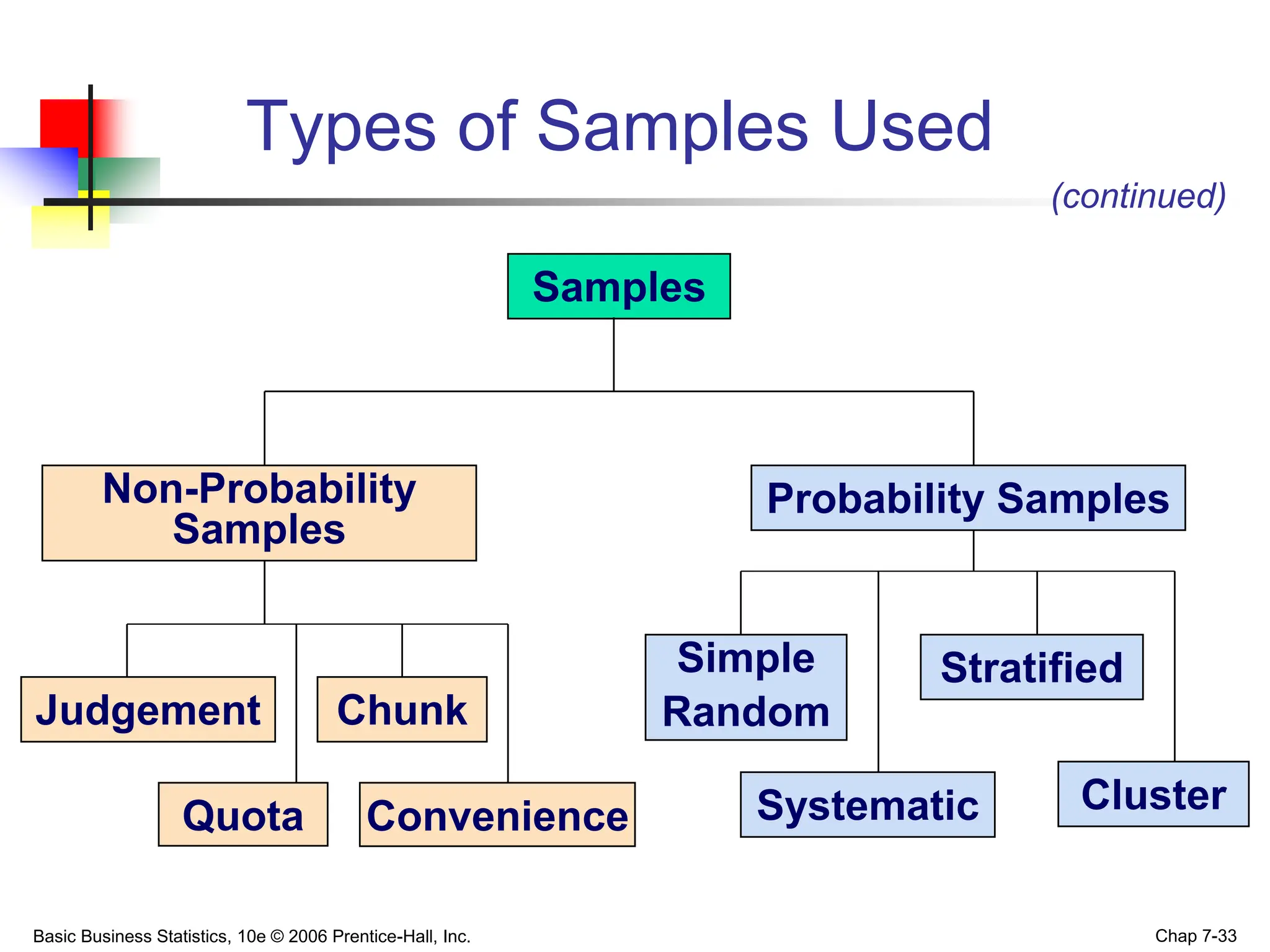
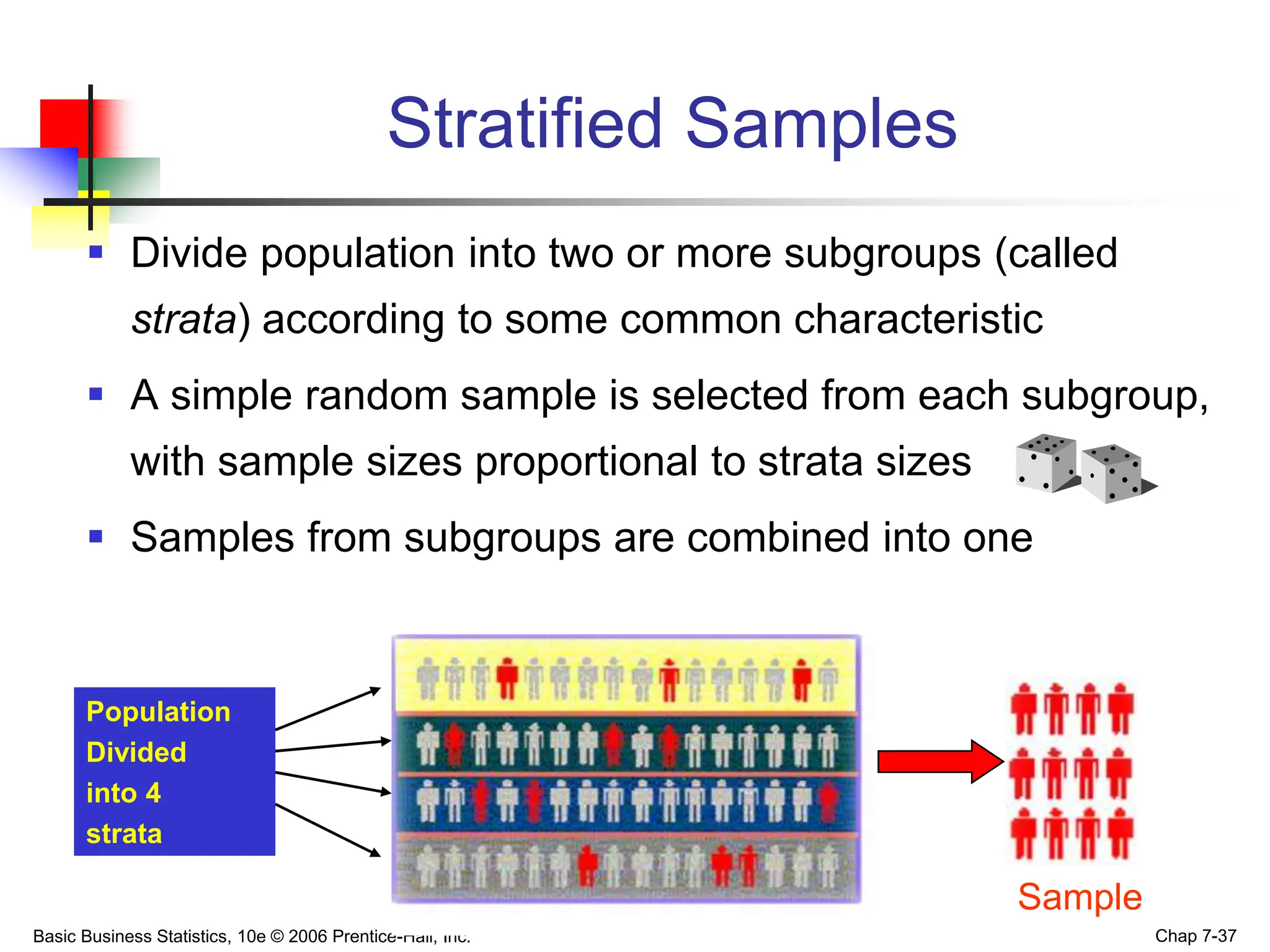
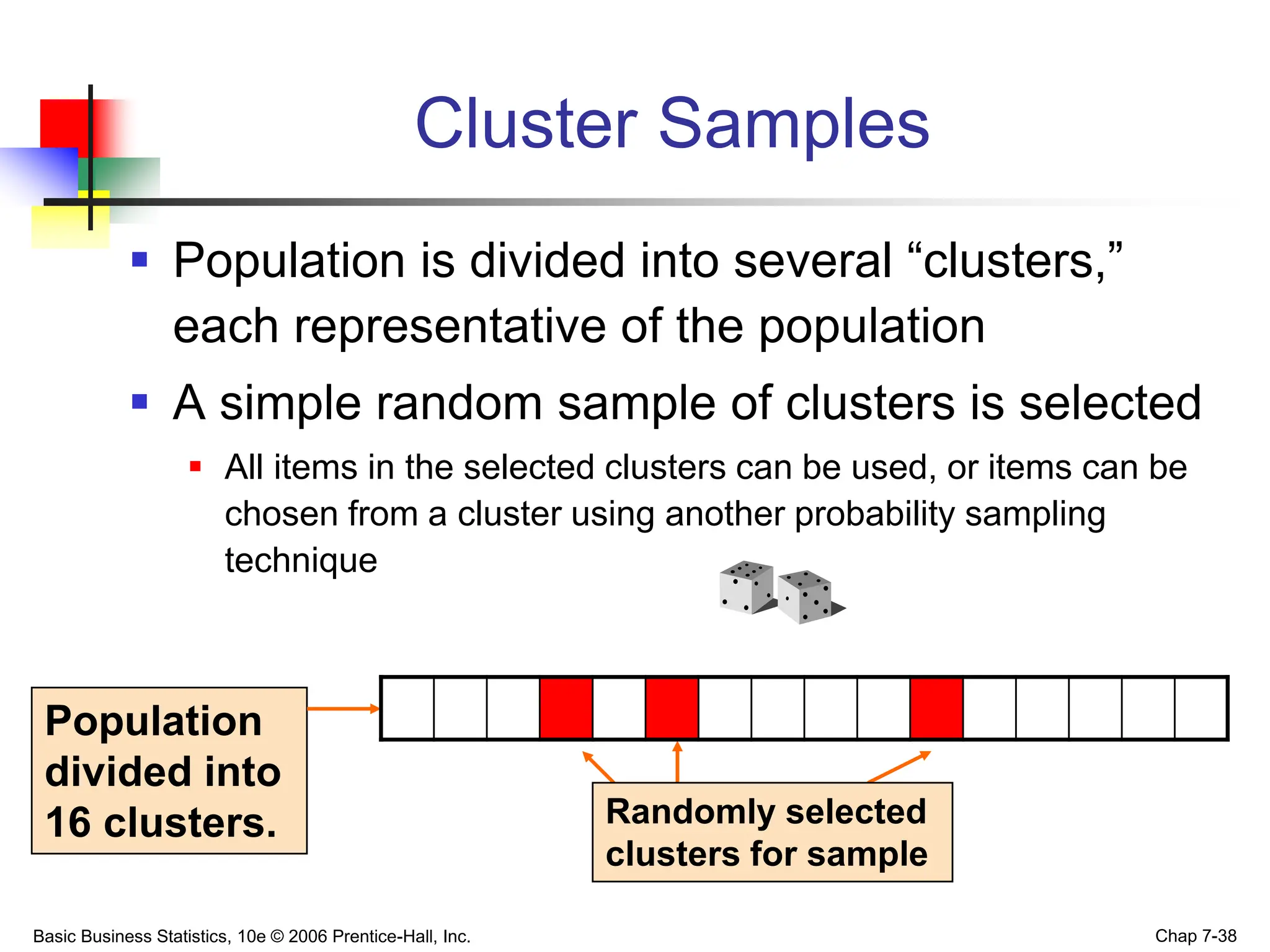
This chapter discusses sampling distributions and their properties. It covers the sampling distribution of the mean and the proportion. The key points are:
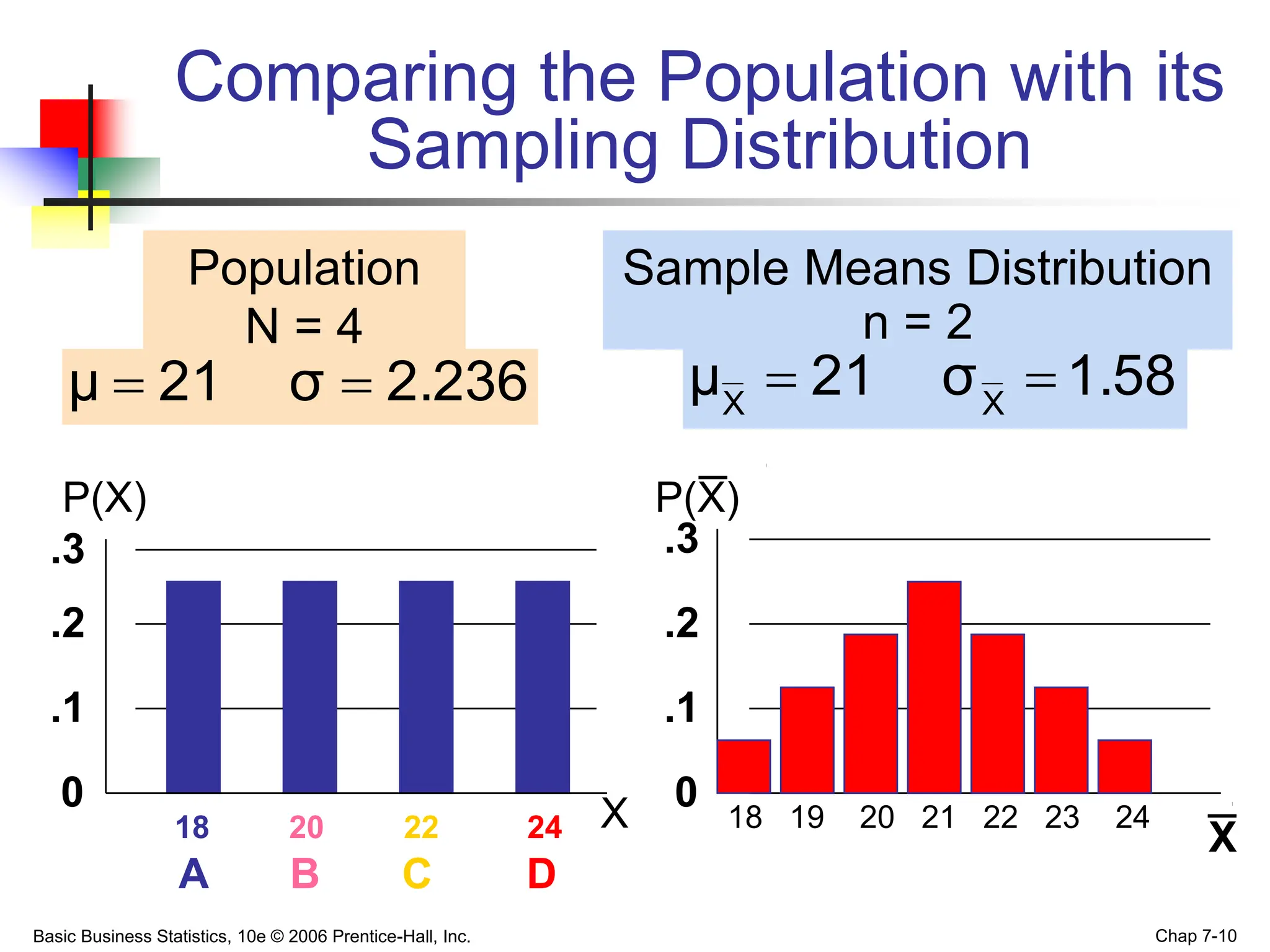
- A sampling distribution describes the distribution of a statistic like the mean from random samples of a population.
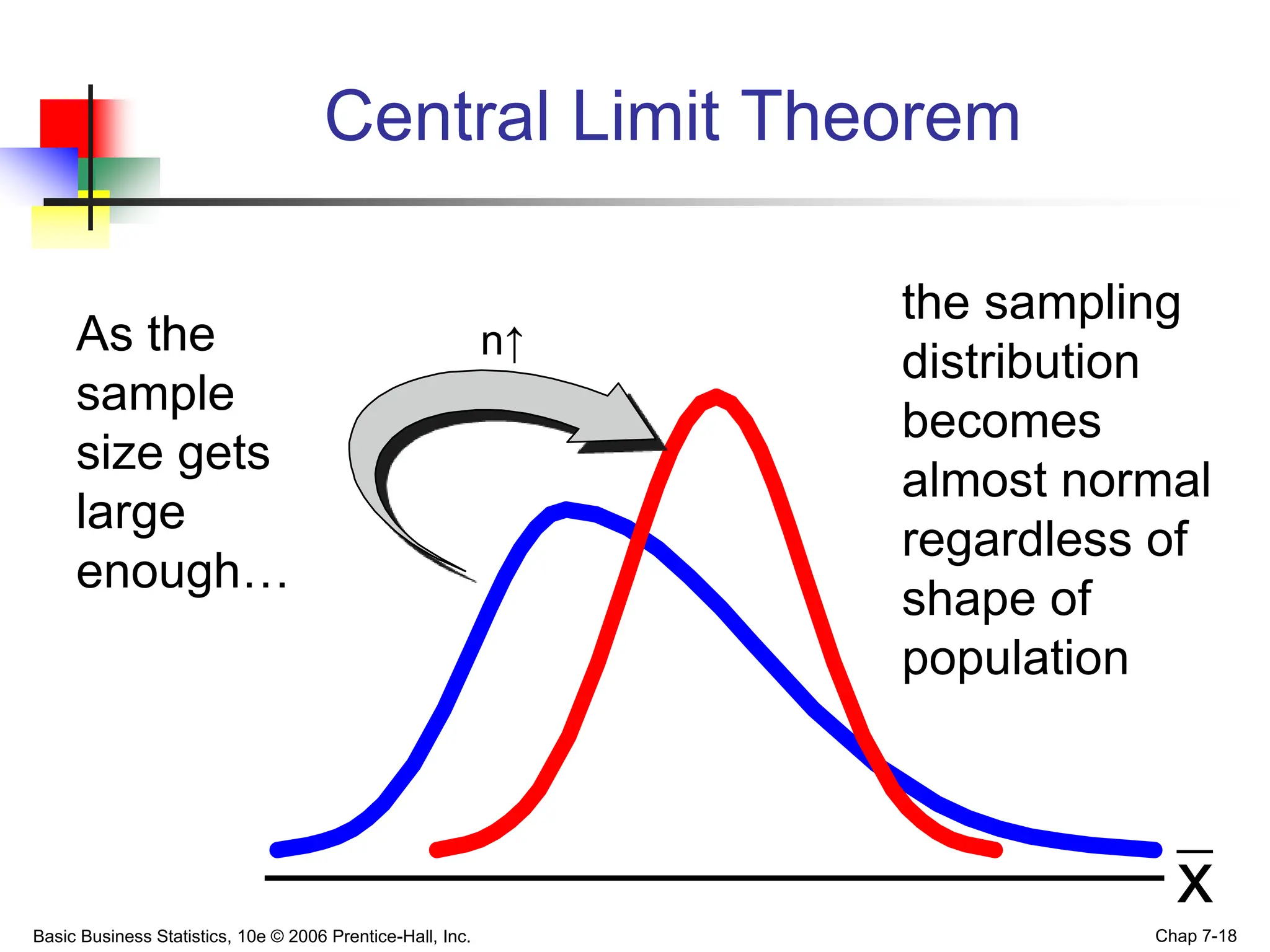
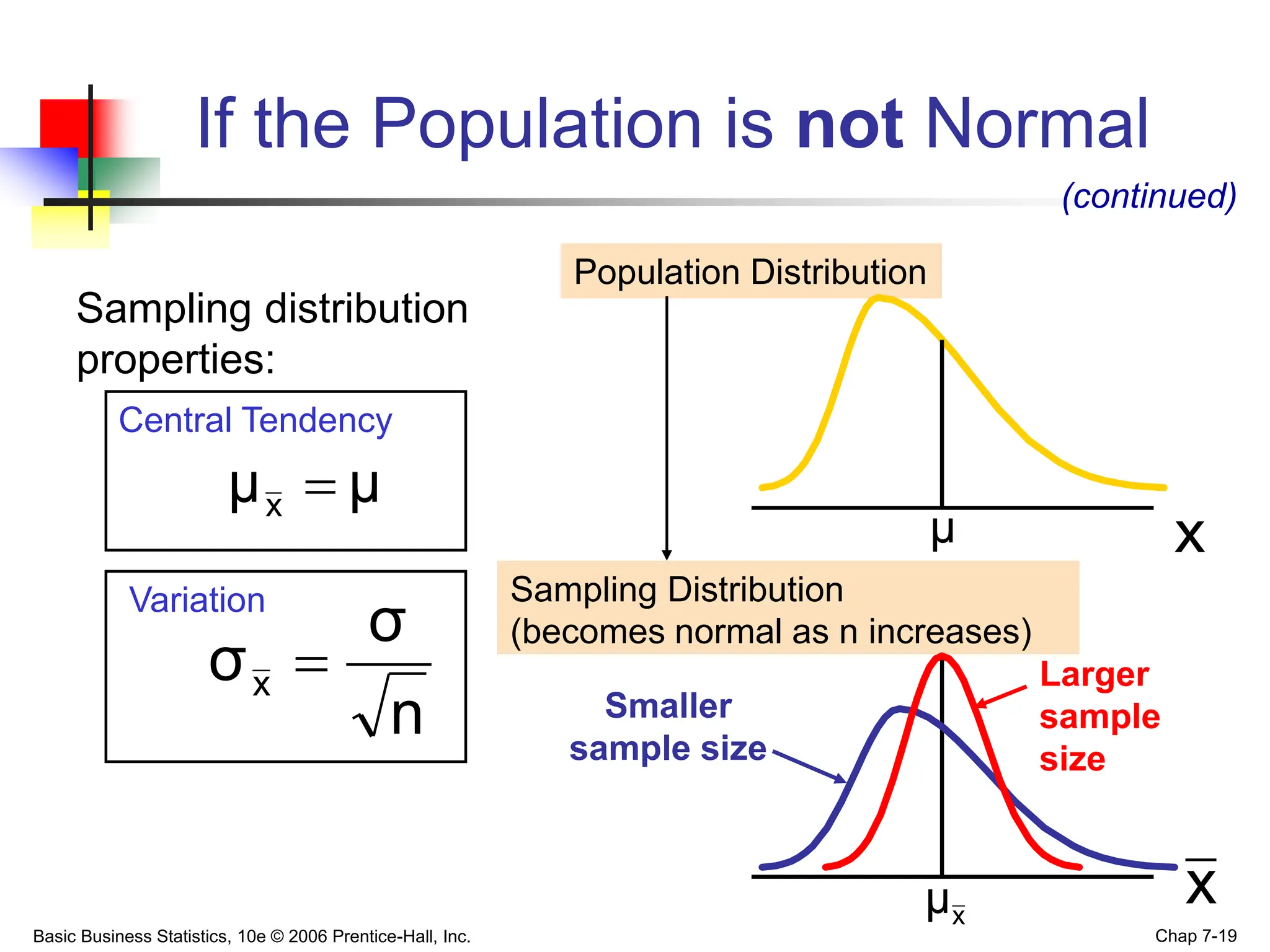
- The Central Limit Theorem states that as sample size increases, the sampling distribution of the mean will approach a normal distribution, even if the population is not normal.
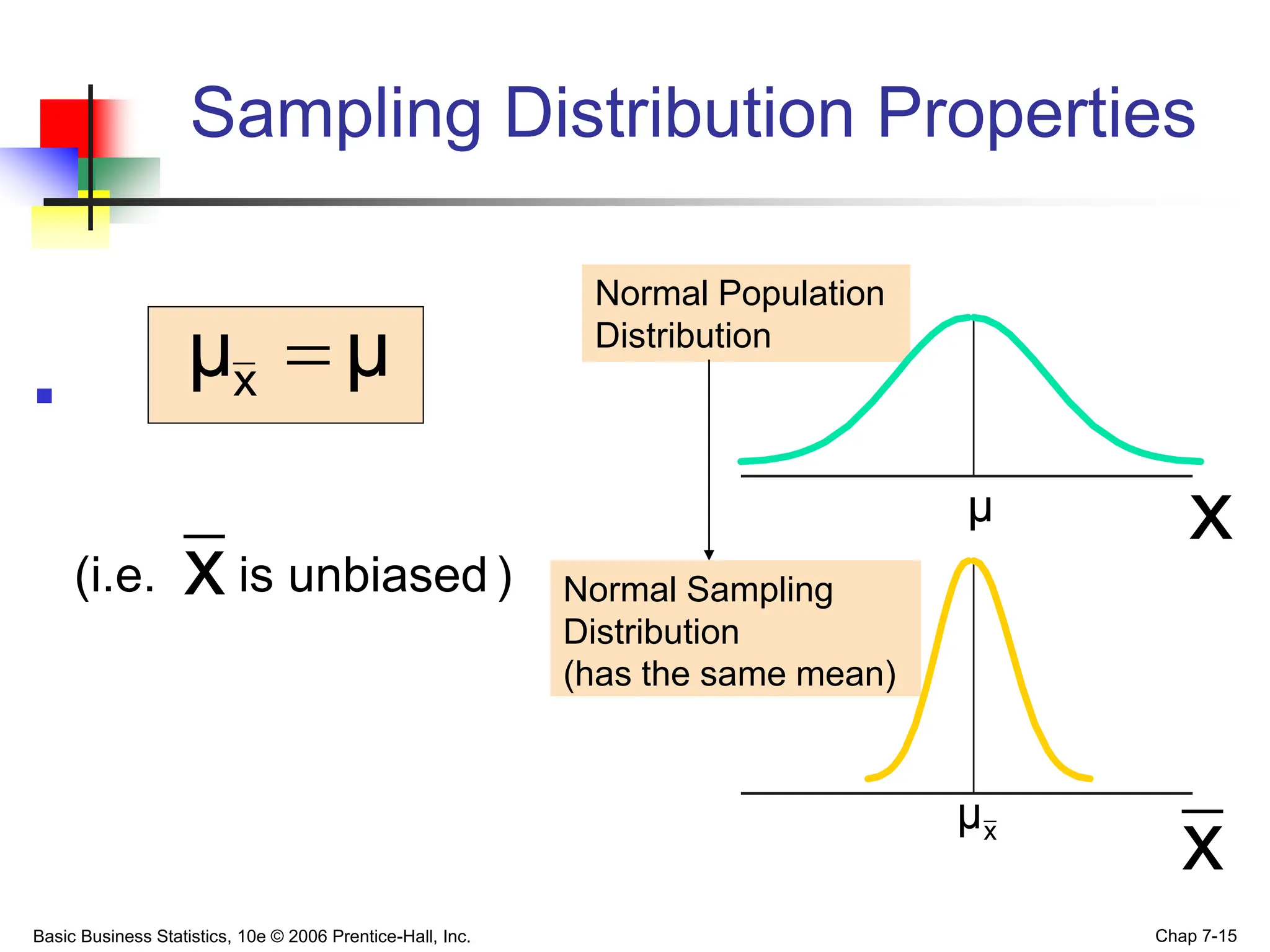
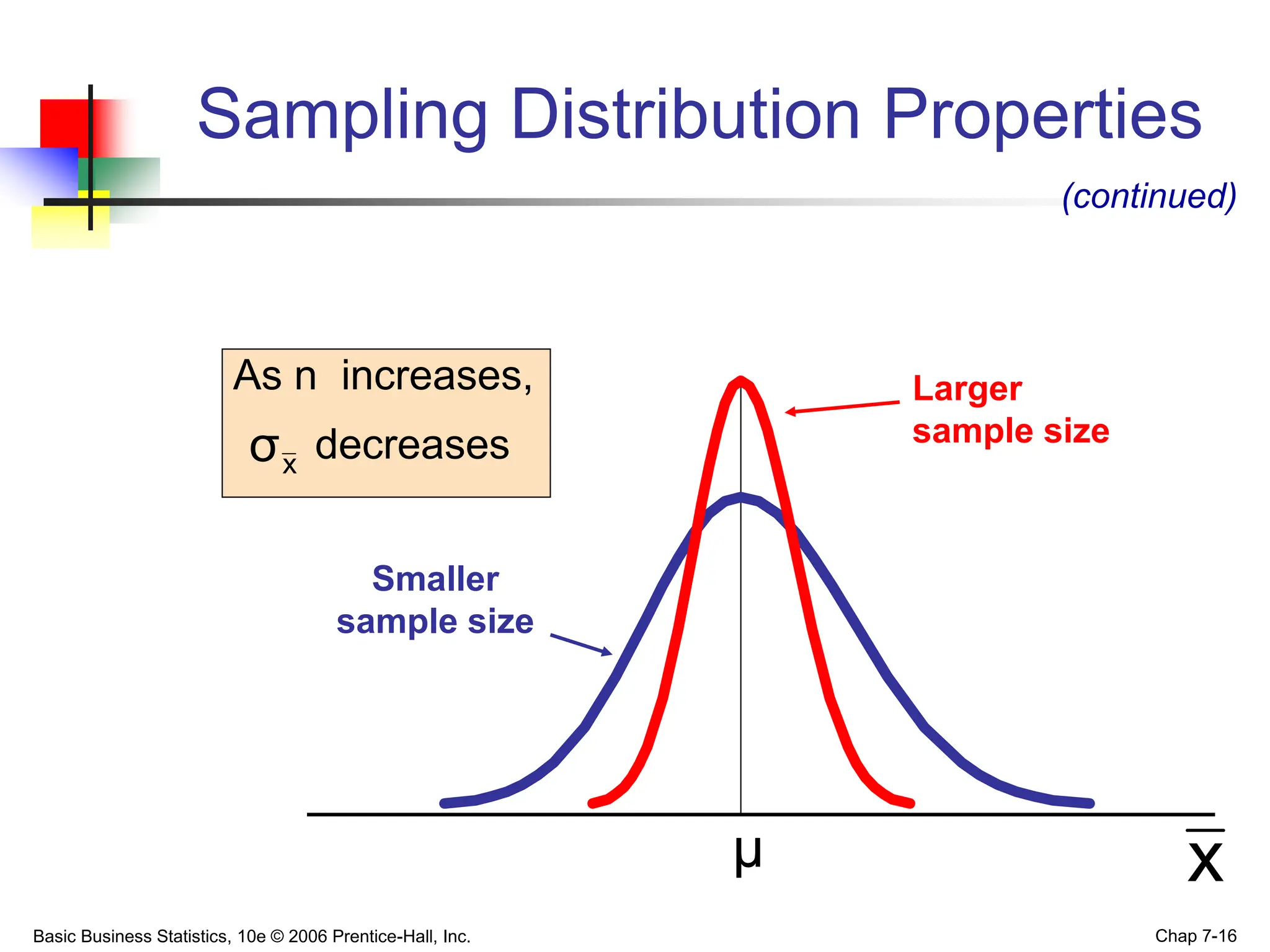
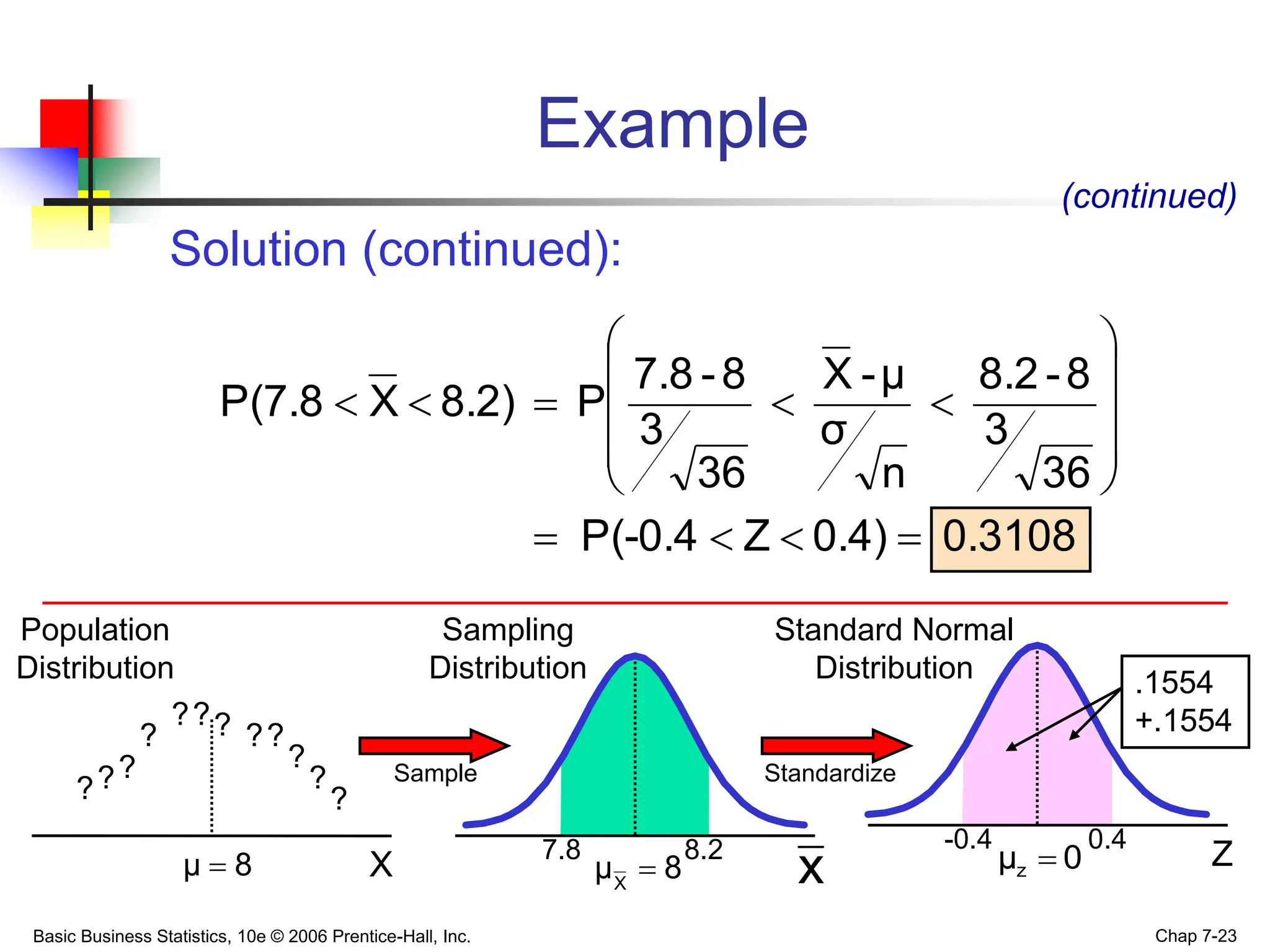
- For the mean, the sampling distribution has a mean equal to the population mean and standard deviation that decreases as sample size increases.
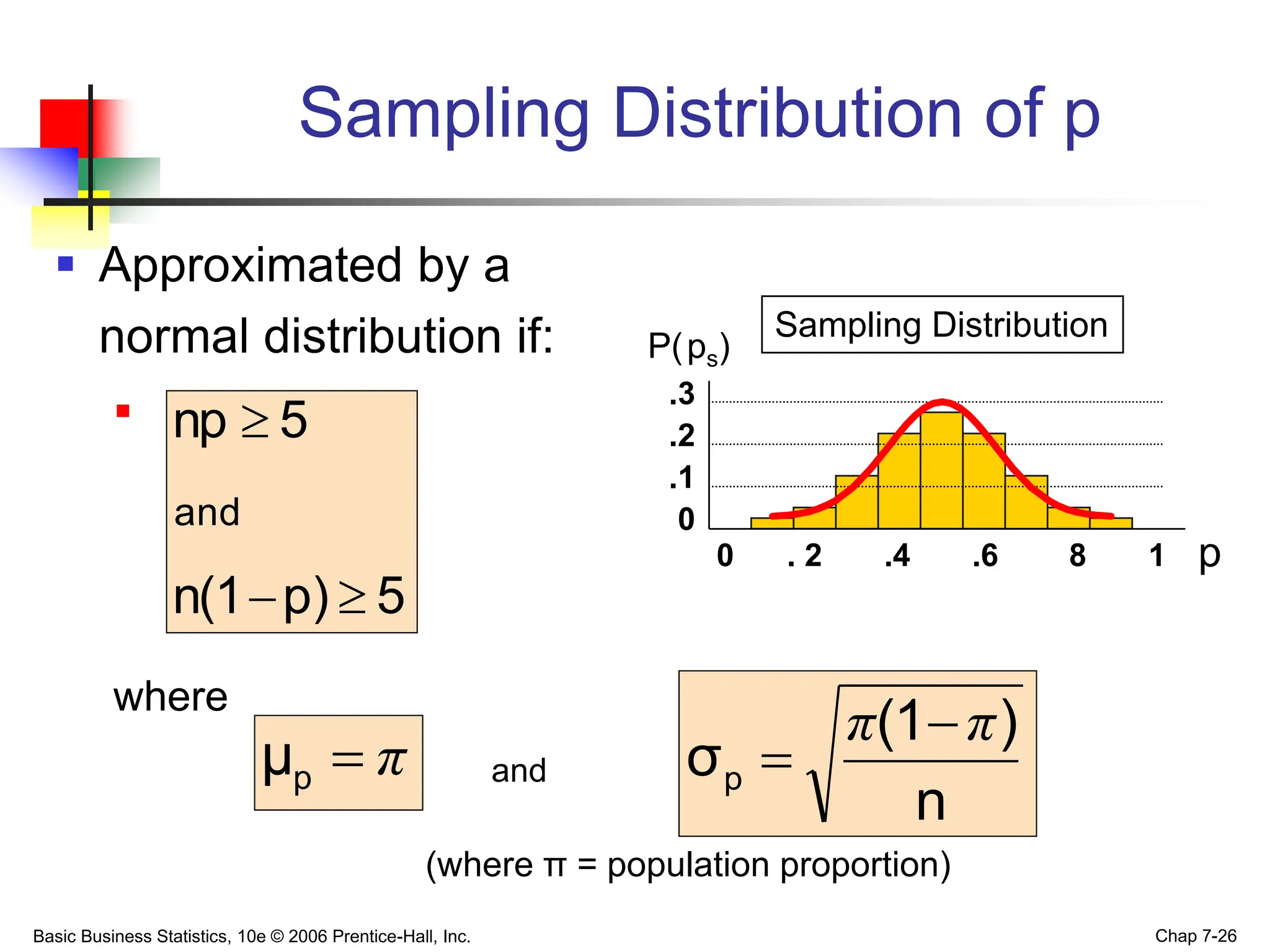
- For a proportion, the sampling distribution can be approximated as normal if sample size n and np or n(1-p) are large enough.