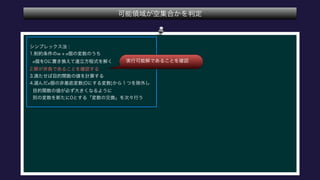
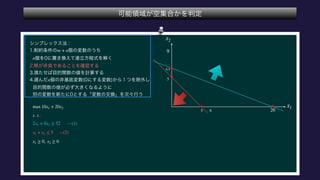
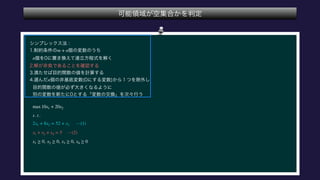
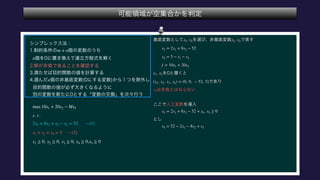
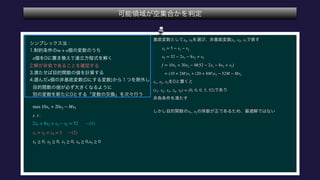
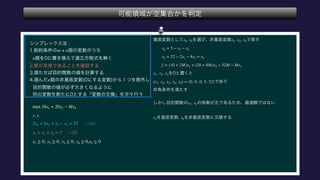
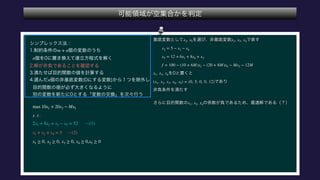
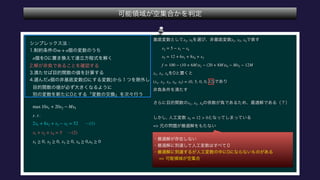
The document describes the optimization of a linear function subject to linear constraints. It involves defining the objective function and constraints, substituting variables to eliminate parameters, and determining the optimal solution satisfies all constraints. The optimal solution is found to be x1=0, x2=5, x3=0, x4=0, x5=12.

1. 10

2. 1.

3. 1.
(a)

5.
m + n
n
n

6.
m + n
n
n
max 10x1 + 20x2
s . t .
2x1 + 8x2 ≥ 52 ⋯(1)
x1 + x2 ≤ 5 ⋯(2)
x1 ≥ 0, x2 ≥ 0
x1
x2
9
6 26
6.5
5
5

7.
m + n
n
n
max 10x1 + 20x2
s . t .
2x1 + 8x2 = 52 + x3 ⋯(1)
x1 + x2 + x4 = 5 ⋯(2)
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0

8.
m + n
n
n
max 10x1 + 20x2 − Mx5
s . t .
2x1 + 8x2 + x3 − x5 = 52 ⋯(1)
x1 + x2 + x4 = 5 ⋯(2)
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0,x5 ≥ 0
x3, x4 x1, x2
x3 = 2x1 + 8x2 − 52
x4 = 5 − x1 − x2
f = 10x1 + 20x2
x1, x2
(x1, x2, x3, x4) = (0, 0, − 52, 5)
x3
x3 = 2x1 + 8x2 − 52 + x5, x5 ≥ 0
x5 = 52 − 2x1 − 8x2 + x3

9.
m + n
n
n
max 10x1 + 20x2 − Mx5
s . t .
2x1 + 8x2 + x3 − x5 = 52 ⋯(1)
x1 + x2 + x4 = 5 ⋯(2)
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0,x5 ≥ 0
x4, x5 x1, x2, x3
x4 = 5 − x1 − x2
x5 = 52 − 2x1 − 8x2 + x3
f = 10x1 + 20x2 − M(52 − 2x1 − 8x2 + x3)
= (10 + 2M)x1 + (20 + 8M)x2 − 52M − Mx3
x1, x2, x3
(x1, x2, x3, x4, x5) = (0, 0, 0, 5, 52)
x1, x2

10.
m + n
n
n
max 10x1 + 20x2 − Mx5
s . t .
2x1 + 8x2 + x3 − x5 = 52 ⋯(1)
x1 + x2 + x4 = 5 ⋯(2)
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0,x5 ≥ 0
x4, x5 x1, x2, x3
x4 = 5 − x1 − x2
x5 = 52 − 2x1 − 8x2 + x3
f = (10 + 2M)x1 + (20 + 8M)x2 − 52M − Mx3
x1, x2, x3
(x1, x2, x3, x4, x5) = (0, 0, 0, 5, 52)
x1, x2
x2 x4

11.
m + n
n
n
max 10x1 + 20x2 − Mx5
s . t .
2x1 + 8x2 + x3 − x5 = 52 ⋯(1)
x1 + x2 + x4 = 5 ⋯(2)
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0,x5 ≥ 0
x2, x5 x1, x3, x4
x2 = 5 − x1 − x4
x5 = 12 + 6x1 + 8x4 + x3
f = 100 − (10 + 6M)x1 − (20 + 8M)x4 − Mx3 − 12M
x1, x3, x4
(x1, x2, x3, x4, x5) = (0, 5, 0, 0, 12)
x1, x3, x4

12.
m + n
n
n
max 10x1 + 20x2 − Mx5
s . t .
2x1 + 8x2 + x3 − x5 = 52 ⋯(1)
x1 + x2 + x4 = 5 ⋯(2)
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0,x5 ≥ 0
x2, x5 x1, x3, x4
x2 = 5 − x1 − x4
x5 = 12 + 6x1 + 8x4 + x3
f = 100 − (10 + 6M)x1 − (20 + 8M)x4 − Mx3 − 12M
x1, x3, x4
(x1, x2, x3, x4, x5) = (0, 5, 0, 0, 12)
x1, x3, x4
x5 = 12 > 0

13.
m + n
n
n
max 10x1 + 20x2 − Mx5
s . t .
2x1 + 8x2 + x3 − x5 = 52 ⋯(1)
x1 + x2 + x4 = 5 ⋯(2)
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0,x5 ≥ 0
x2, x5 x1, x3, x4
x2 = 5 − x1 − x4
x5 = 12 + 6x1 + 8x4 + x3
f = 100 − (10 + 6M)x1 − (20 + 8M)x4 − Mx3 − 12M
x1, x3, x4
(x1, x2, x3, x4, x5) = (0, 5, 0, 0, 12)
x1, x3, x4
x5 = 12 > 0

15. See you next time
10