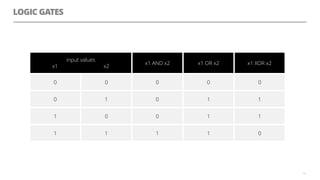
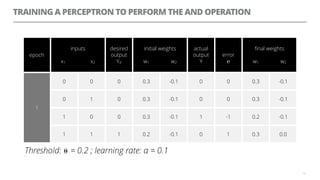
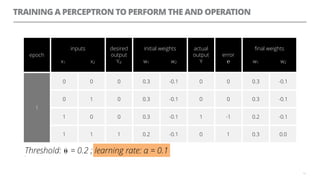
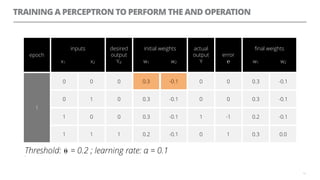
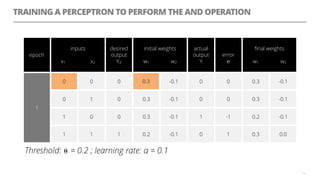
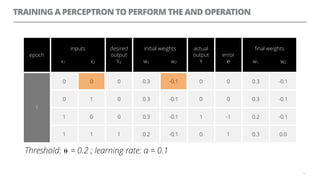
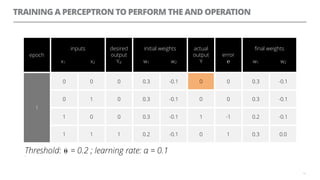
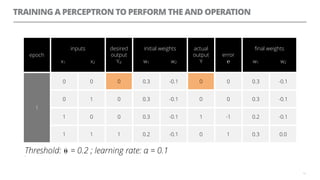
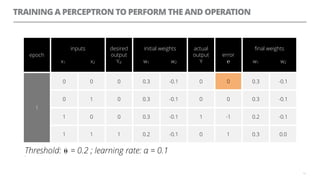
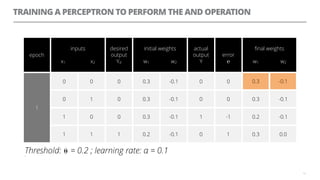
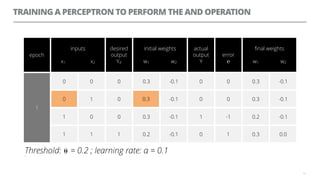
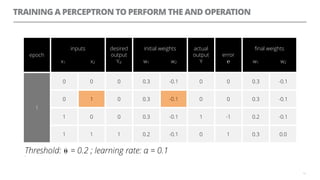
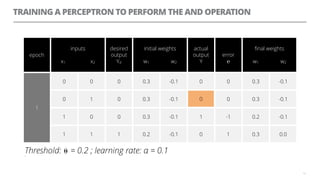
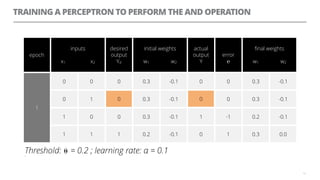
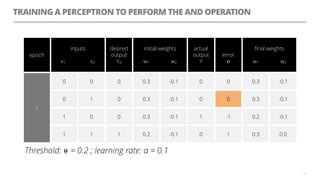
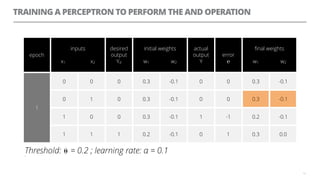
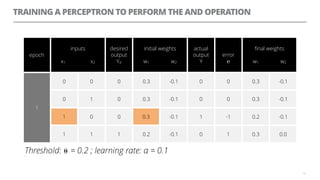
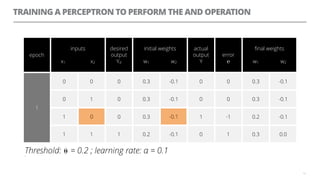
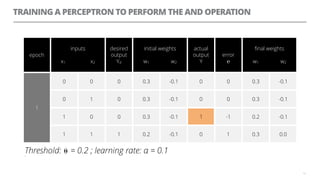
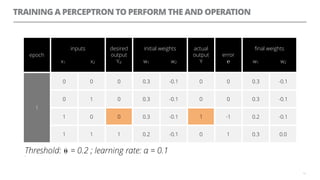
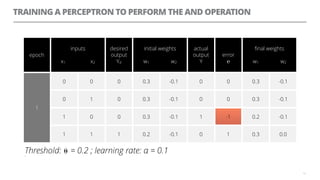
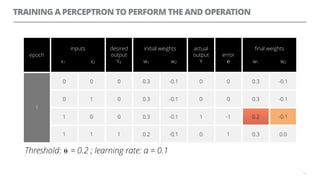
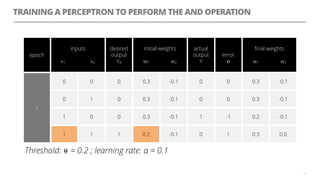
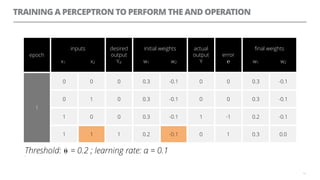
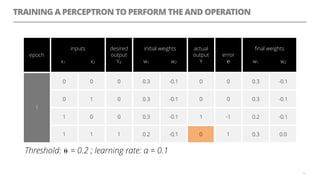
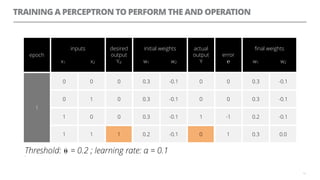
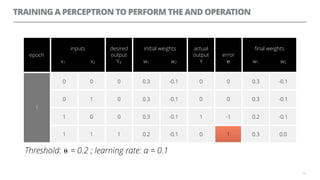
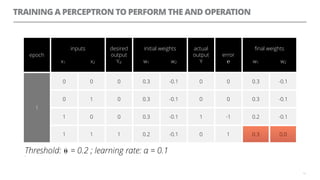
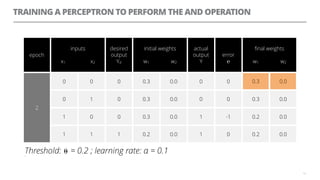
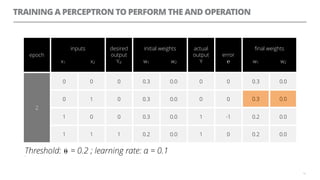
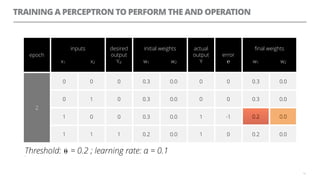
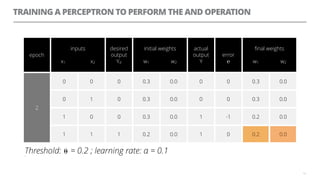
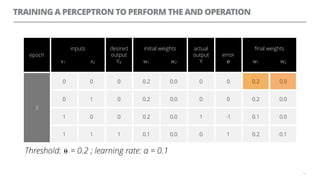
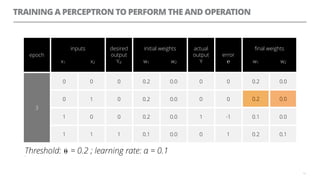
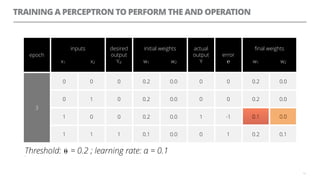
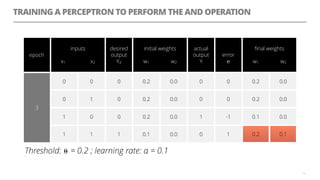
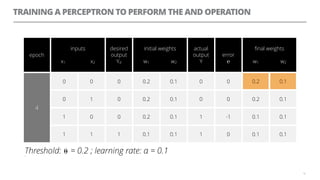
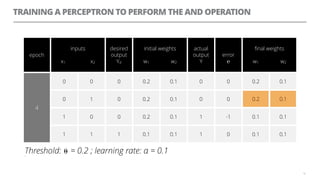
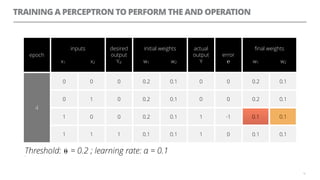
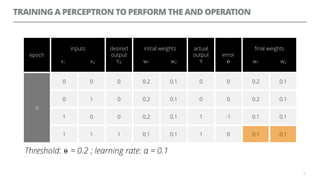
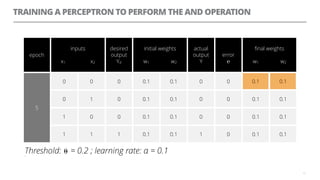
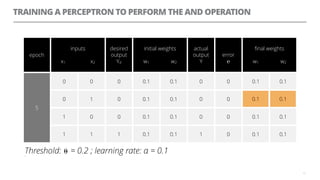
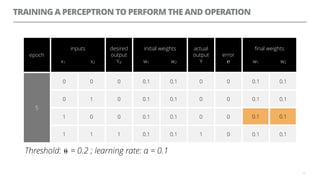
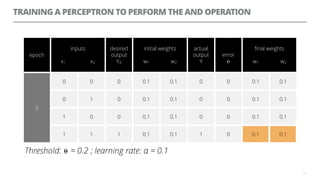
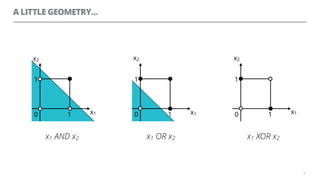
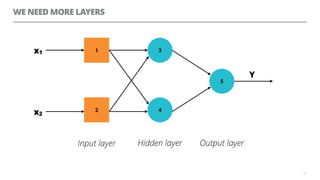
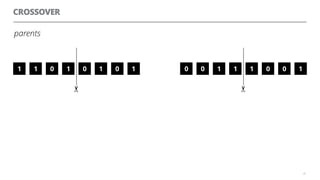
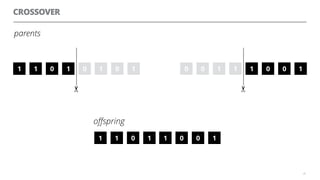
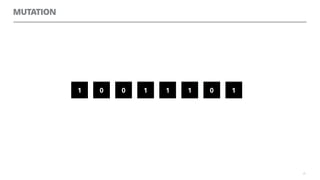
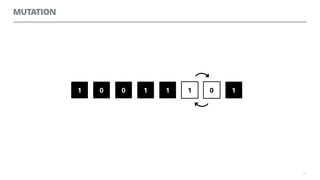
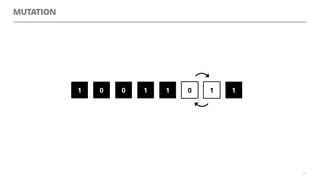
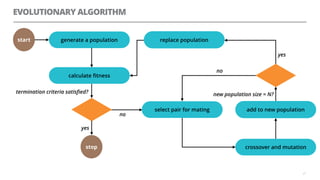
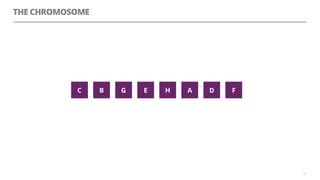
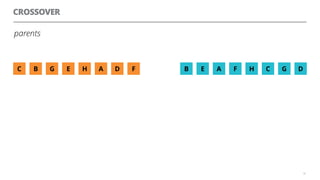
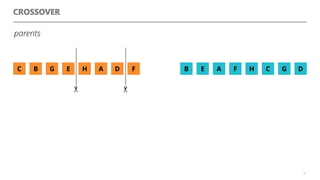
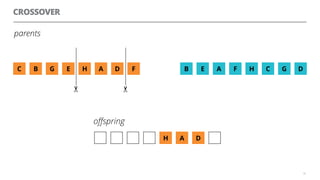
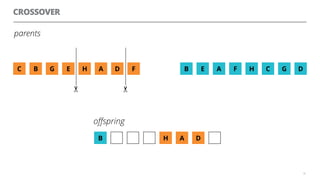
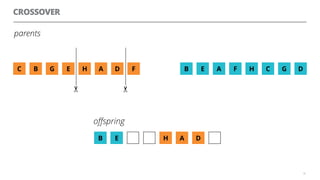
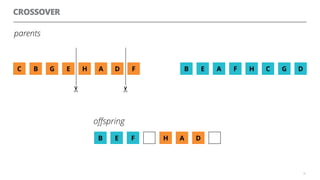
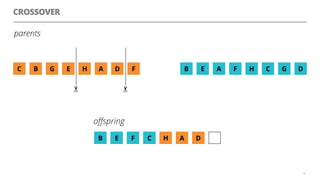
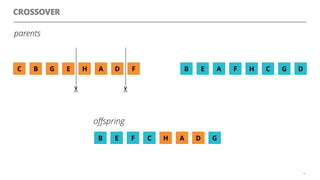
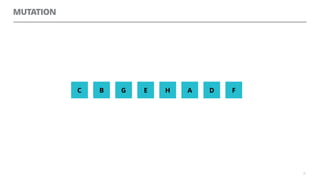
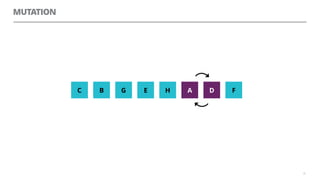
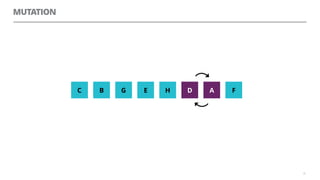
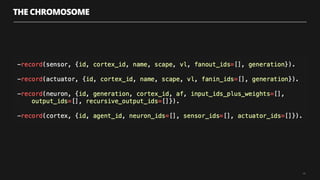
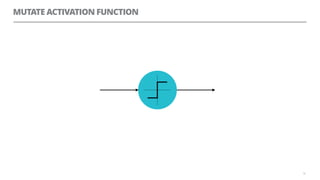
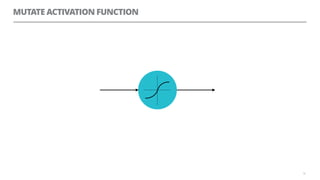
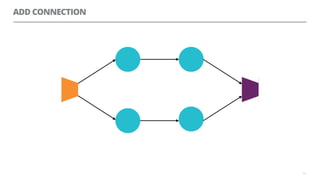
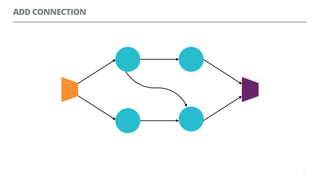
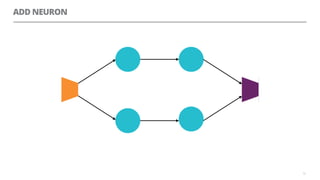
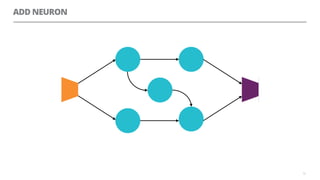
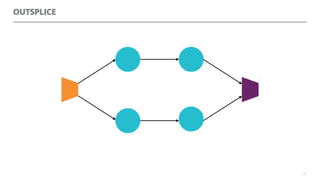
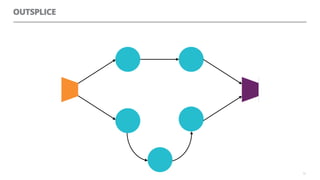
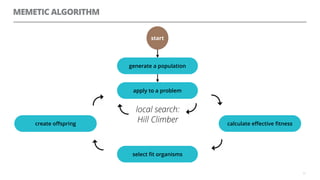
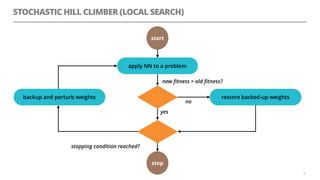
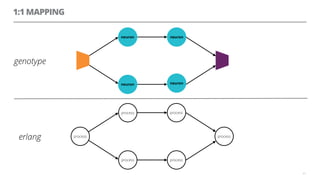
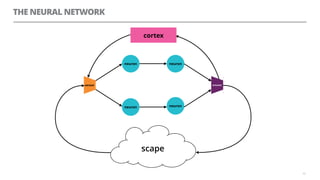
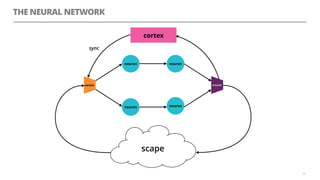
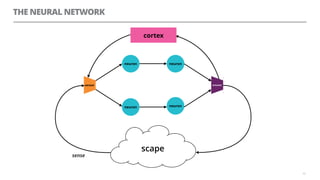
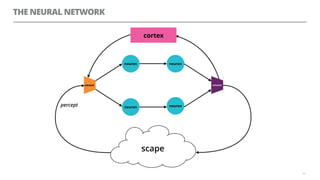
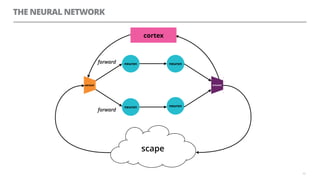
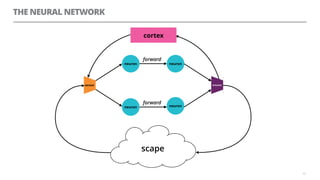
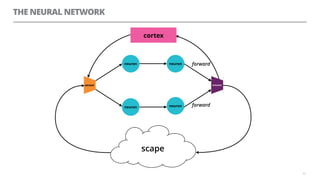
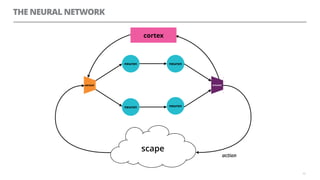
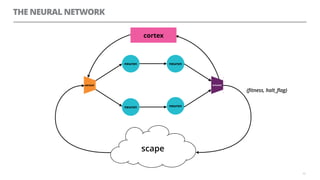
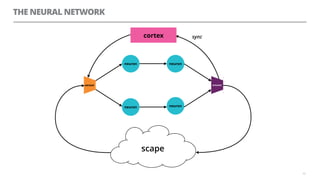
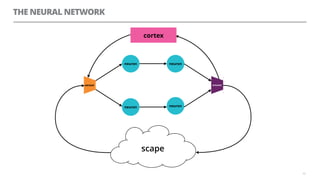
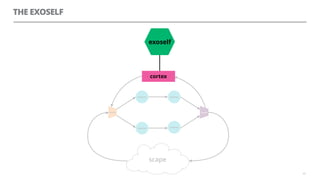
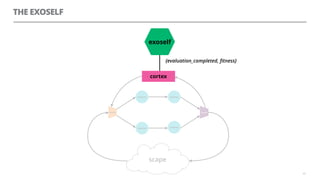
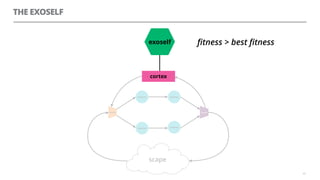
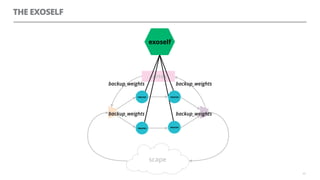
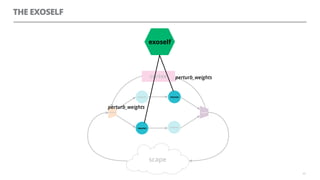
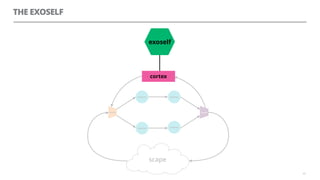
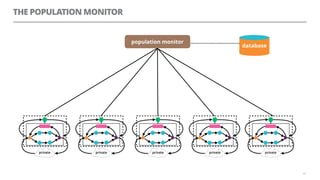
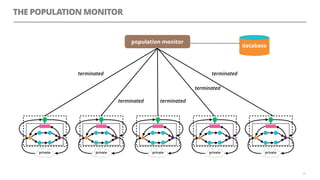
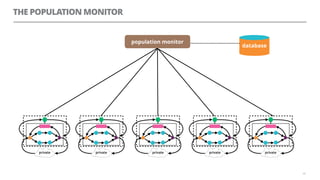
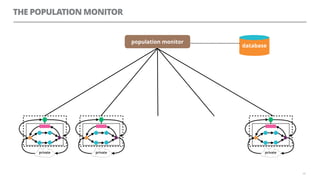
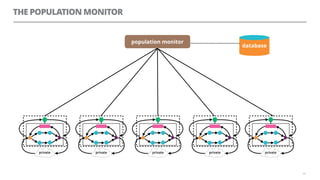
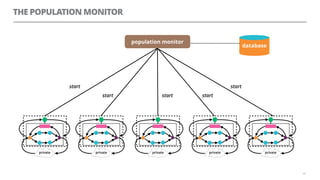
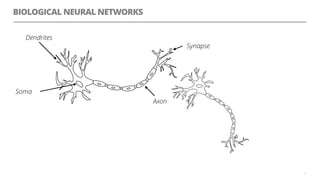
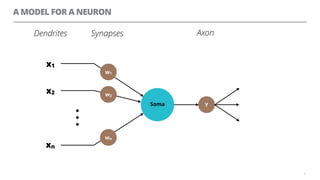
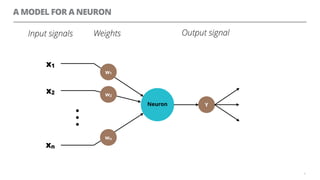
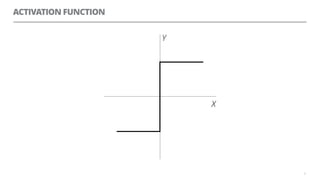
The document discusses artificial neural networks and how they can be trained using a perceptron learning algorithm. It provides an example of training a perceptron to perform the logical AND operation. Over multiple epochs, the perceptron's weights are adjusted based on its errors to correctly output a 1 only when both the x1 and x2 inputs are 1.

1. J e r o e n S o e t e r s
NEUROEVOLUTION
A hitchhiker’s guide to neuroevolution in
Erlang.

2. MEET GARY
2

3. WHAT IS MACHINE LEARNING?
• Artificial Neural Networks
• Genetic Algorithms
3

4. ARTIFICIAL NEURAL
NETWORKS
4

5. BIOLOGICAL NEURAL NETWORKS
5
Dendrites
Soma
Axon
Synapse

6. A MODEL FOR A NEURON
6
Y
w1
w2
wn
x1
x2
xn
Dendrites Synapses Axon
Soma

7. A MODEL FOR A NEURON
6
Y
w1
w2
wn
x1
x2
xn
Input signals Weights Output signal
Neuron

8. HOW DOES THE NEURON DETERMINE IT’S OUTPUT?
Y =sign ∑xiwi - ⍬
7
n=1
n

9. ACTIVATION FUNCTION
8
X
Y

10. MEET FRANK
9

11. PERCEPTRON LEARNING RULE
℮(p) = Yd(p) - Y(p)
wi(p + 1) = wi(p) + α • wi(p) • ℮(p)
=
10

12. PERCEPTRON TRAINING ALGORITHM
11
weight training
start
stop
weights converged? yes
no
set weights and threshold to
random values [-0.5, 0.5]
activate the perceptron

13. LOGIC GATES
12
input values
x1 x2
x1 AND x2 x1 OR x2 x1 XOR x2
0 0 0 0 0
0 1 0 1 1
1 0 0 1 1
1 1 1 1 0

14. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=

15. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=

16. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=

17. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.3 -0.1

18. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0 0.3

19. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0 -0.1

20. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0

21. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
00

22. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0

23. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.3 -0.1

24. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0 0.3

25. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
1 -0.1

26. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0

27. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
00

28. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0

29. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.3 -0.1

30. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
1 0.3

31. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0 -0.1

32. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
1

33. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
10

34. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
-1

35. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.2 -0.1

36. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
1 0.2

37. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
1 -0.1

38. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0

39. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
01

40. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
1

41. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
13
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
1
0 0 0 0.3 -0.1 0 0 0.3 -0.1
0 1 0 0.3 -0.1 0 0 0.3 -0.1
1 0 0 0.3 -0.1 1 -1 0.2 -0.1
1 1 1 0.2 -0.1 0 1 0.3 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.3 0.0

42. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
14
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
2
0 0 0 0.3 0.0 0 0 0.3 0.0
0 1 0 0.3 0.0 0 0 0.3 0.0
1 0 0 0.3 0.0 1 -1 0.2 0.0
1 1 1 0.2 0.0 1 0 0.2 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.3 0.0

43. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
14
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
2
0 0 0 0.3 0.0 0 0 0.3 0.0
0 1 0 0.3 0.0 0 0 0.3 0.0
1 0 0 0.3 0.0 1 -1 0.2 0.0
1 1 1 0.2 0.0 1 0 0.2 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.3 0.0

44. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
14
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
2
0 0 0 0.3 0.0 0 0 0.3 0.0
0 1 0 0.3 0.0 0 0 0.3 0.0
1 0 0 0.3 0.0 1 -1 0.2 0.0
1 1 1 0.2 0.0 1 0 0.2 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.2 0.0

45. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
14
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
2
0 0 0 0.3 0.0 0 0 0.3 0.0
0 1 0 0.3 0.0 0 0 0.3 0.0
1 0 0 0.3 0.0 1 -1 0.2 0.0
1 1 1 0.2 0.0 1 0 0.2 0.0
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.2 0.0

46. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
15
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
3
0 0 0 0.2 0.0 0 0 0.2 0.0
0 1 0 0.2 0.0 0 0 0.2 0.0
1 0 0 0.2 0.0 1 -1 0.1 0.0
1 1 1 0.1 0.0 0 1 0.2 0.1
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.2 0.0

47. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
15
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
3
0 0 0 0.2 0.0 0 0 0.2 0.0
0 1 0 0.2 0.0 0 0 0.2 0.0
1 0 0 0.2 0.0 1 -1 0.1 0.0
1 1 1 0.1 0.0 0 1 0.2 0.1
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.2 0.0

48. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
15
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
3
0 0 0 0.2 0.0 0 0 0.2 0.0
0 1 0 0.2 0.0 0 0 0.2 0.0
1 0 0 0.2 0.0 1 -1 0.1 0.0
1 1 1 0.1 0.0 0 1 0.2 0.1
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.1 0.0

49. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
15
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
3
0 0 0 0.2 0.0 0 0 0.2 0.0
0 1 0 0.2 0.0 0 0 0.2 0.0
1 0 0 0.2 0.0 1 -1 0.1 0.0
1 1 1 0.1 0.0 0 1 0.2 0.1
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.2 0.1

50. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
16
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
4
0 0 0 0.2 0.1 0 0 0.2 0.1
0 1 0 0.2 0.1 0 0 0.2 0.1
1 0 0 0.2 0.1 1 -1 0.1 0.1
1 1 1 0.1 0.1 1 0 0.1 0.1
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.2 0.1

51. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
16
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
4
0 0 0 0.2 0.1 0 0 0.2 0.1
0 1 0 0.2 0.1 0 0 0.2 0.1
1 0 0 0.2 0.1 1 -1 0.1 0.1
1 1 1 0.1 0.1 1 0 0.1 0.1
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.2 0.1

52. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
16
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
4
0 0 0 0.2 0.1 0 0 0.2 0.1
0 1 0 0.2 0.1 0 0 0.2 0.1
1 0 0 0.2 0.1 1 -1 0.1 0.1
1 1 1 0.1 0.1 1 0 0.1 0.1
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.1 0.1

53. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
16
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
4
0 0 0 0.2 0.1 0 0 0.2 0.1
0 1 0 0.2 0.1 0 0 0.2 0.1
1 0 0 0.2 0.1 1 -1 0.1 0.1
1 1 1 0.1 0.1 1 0 0.1 0.1
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.1 0.1

54. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
17
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
5
0 0 0 0.1 0.1 0 0 0.1 0.1
0 1 0 0.1 0.1 0 0 0.1 0.1
1 0 0 0.1 0.1 0 0 0.1 0.1
1 1 1 0.1 0.1 1 0 0.1 0.1
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.1 0.1

55. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
17
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
5
0 0 0 0.1 0.1 0 0 0.1 0.1
0 1 0 0.1 0.1 0 0 0.1 0.1
1 0 0 0.1 0.1 0 0 0.1 0.1
1 1 1 0.1 0.1 1 0 0.1 0.1
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.1 0.1

56. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
17
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
5
0 0 0 0.1 0.1 0 0 0.1 0.1
0 1 0 0.1 0.1 0 0 0.1 0.1
1 0 0 0.1 0.1 0 0 0.1 0.1
1 1 1 0.1 0.1 1 0 0.1 0.1
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.1 0.1

57. TRAINING A PERCEPTRON TO PERFORM THE AND OPERATION
17
epoch
inputs
x1 x2
desired
output
Yd
initial weights
w1 w2
actual
output
Y
error
℮
final weights
w1 w2
5
0 0 0 0.1 0.1 0 0 0.1 0.1
0 1 0 0.1 0.1 0 0 0.1 0.1
1 0 0 0.1 0.1 0 0 0.1 0.1
1 1 1 0.1 0.1 1 0 0.1 0.1
Threshold: ⍬ = 0.2 ; learning rate: α = 0.1=
0.1 0.1

58. A LITTLE GEOMETRY…
18
0 1
1
x2
x1 0 1
1
x2
x10 1
1
x2
x1
x1 AND x2 x1 OR x2 x1 XOR x2

59. WE NEED MORE LAYERS
19
3
4
5
1
2
Input layer Hidden layer Output layer
x1
x2
Y

60. PROBLEMS WITH BACK PROPAGATION
•a training set of sufficient size is required
•topology of the network needs to be known in advance
•no recurrent connections are allowed
•activation function must be differentiable
Does not emulate the biological world
20

61. EVOLUTIONARY
COMPUTATION
21

62. MEET JOHN
22

63. THE CHROMOSOME
23
10 11 101 0

64. 1 1000 11 0
CROSSOVER
24
0 111 0 11 0 1 100 1 10 0
parents

65. 1 1000 11 0
CROSSOVER
24
0 111 0 11 0 1 100 1 10 0
✂
parents
✂

66. 1 1000 11 0
1 10 00 111
offspring
CROSSOVER
24
0 111 1 10 0
✂
parents
✂

67. MUTATION
25
A D10 11 101 0

68. MUTATION
25
A DA D10 11 101 01 0

69. MUTATION
25
A DA D10 11 101 01 00 1

70. EVOLUTIONARY ALGORITHM
•represent the candidate solution as a chromosome
•chose the initial population size N, crossover probability (Pc) and mutation
probability (Pm)
•define a fitness function to measure the performance of the chromosome
•define the genetic operators for the chromosome
26

71. EVOLUTIONARY ALGORITHM
27
start
stop
generate a population
calculate fitness
termination criteria satisfied?
yes
no
new population size = N?
crossover and mutation
select pair for mating add to new population
replace population
no
yes

72. TRAVELING SALESMAN
28
A
B
D
F
G
C
E
H

73. EVOLUTIONARY ALGORITHM
•represent the candidate solution as a chromosome
•define a fitness function to measure the performance of the chromosome
•define the genetic operators for the chromosome
•chose the initial population size N, crossover probability Pc and mutation
probability Pm
29

74. THE CHROMOSOME
30
HG FE ABC D

75. EVOLUTIONARY ALGORITHM
•represent the candidate solution as a chromosome
•define a fitness function to measure the performance of the
chromosome
•define the genetic operators for the chromosome
•chose the initial population size N, crossover probability Pc and mutation
probability Pm
31

76. FITNESS FUNCTION
Fitness = 1 / total distance
32

77. EVOLUTIONARY ALGORITHM
•represent the candidate solution as a chromosome
•define a fitness function to measure the performance of the chromosome
•define the genetic operators for the chromosome
•chose the initial population size N, crossover probability Pc and mutation
probability Pm
33

78. CROSSOVER
34
G EBC H FA D A FEB H DC G
parents

79. CROSSOVER
34
G EBC H FA D A FEB H DC G
✂
✂
parents

80. H A D
offspring
CROSSOVER
34
G EBC H FA D A FEB H DC G
✂
✂
parents

81. H A D
offspring
CROSSOVER
34
G EBC H FA D A FEB H DC G
✂
✂
parents
B

82. H A D
offspring
CROSSOVER
34
G EBC H FA D A FEB H DC G
✂
✂
parents
B E

83. H A D
offspring
CROSSOVER
34
G EBC H FA D A FEB H DC G
✂
✂
parents
B E F

84. H A D
offspring
CROSSOVER
34
G EBC H FA D A FEB H DC G
✂
✂
parents
B E F C

85. H A D
offspring
CROSSOVER
34
G EBC H FA D A FEB H DC G
✂
✂
parents
B E F C G

86. MUTATION
35
HG FE ABC D

87. MUTATION
35
HG FE ABC DA D

88. MUTATION
35
HG FE ABC DA DAD

89. EVOLUTIONARY ALGORITHM
•represent the candidate solution as a chromosome
•define a fitness function to measure the performance of the chromosome
•define the genetic operators for the chromosome
•chose the initial population size N, crossover probability Pc and
mutation probability Pm
36

90. DEMO
37

91. DEMO
37

92. NEUROEVOLUTION
38

93. MEET GENE
39

94. SIMULATION
•inputs (sensors)
•outputs (actuators)
•fitness function
40

95. CLEANING ROBOT
41

96. FOREX TRADING
42

97. AND LOTS MORE…
•data compression
•training NPCs in a video game
•cyber warfare
43

98. EVOLUTIONARY ALGORITHM
•represent the candidate solution as a chromosome
•define a fitness function to measure the performance of the chromosome
•define the genetic operators for the chromosome
•chose the initial population size N, crossover probability Pc and mutation
probability Pm
44

99. THE CHROMOSOME
45

100. EVOLUTIONARY ALGORITHM
•represent the candidate solution as a chromosome
•define a fitness function to measure the performance of the
chromosome
•define the genetic operators for the chromosome
•chose the initial population size N, crossover probability Pc and mutation
probability Pm
46

101. FITNESS FUNCTION
Fitness = performance of network on an actual problem
47

102. EVOLUTIONARY ALGORITHM
•represent the candidate solution as a chromosome
•define a fitness function to measure the performance of the chromosome
•define the genetic operators for the chromosome
•chose the initial population size N, crossover probability Pc and mutation
probability Pm
48

103. CROSSOVER
Crossover doesn’t work for large neural nets!
49

104. MUTATE ACTIVATION FUNCTION
50

105. MUTATE ACTIVATION FUNCTION
50

106. ADD CONNECTION
51

107. ADD CONNECTION
51

108. ADD NEURON
52

109. ADD NEURON
52

110. OUTSPLICE
53

111. OUTSPLICE
53

112. MUTATION OPERATORS
and lots more…
54

113. EVOLUTIONARY ALGORITHM
•represent the candidate solution as a chromosome
•define a fitness function to measure the performance of the chromosome
•define the genetic operators for the chromosome
•chose the initial population size N, crossover probability Pc and
mutation probability Pm
55

114. RANDOM IMPACT MUTATION
Number of mutations = random(1, network size)
56

115. MEMETIC ALGORITHM
57
apply to a problem
start
generate a population
local search:
Hill Climber calculate effective fitness
select fit organisms
create offspring

116. STOCHASTIC HILL CLIMBER (LOCAL SEARCH)
58
start
new fitness > old fitness?
yes
no
stopping condition reached?
stop
apply NN to a problem
backup and perturb weights restore backed-up weights

117. A LANGUAGE FOR NEUROEVOLUTION
•The system must be able to handle very large numbers of concurrent activities
•Actions must be performed at a certain point in time or within a certain time
•Systems may be distributed over several computers
•The system is used to control hardware
•The software systems are very large
59

118. A LANGUAGE FOR NEUROEVOLUTION
59
•The system exhibits complex functionality such as, feature interaction.
•The systems should be in continuous operation for many years.
•Software maintenance (reconfiguration, etc) should be performed without
stopping the system.
•There are stringent quality, and reliability requirements.
•Fault tolerance

119. A LANGUAGE FOR NEUROEVOLUTION
59
•The system exhibits complex functionality such as, feature interaction.
•The systems should be in continuous operation for many years.
•Software maintenance (reconfiguration, etc) should be performed without
stopping the system.
•There are stringent quality, and reliability requirements.
•Fault tolerance
Bjarne Dacker. Erlang - A New Programming Language. Ericsson Review,
no 2, 1993.

120. MEET JOE
60

121. 1:1 MAPPING
61
neuron
neuronneuron
neuron
process process
process process
processprocess
genotype
erlang

122. THE NEURAL NETWORK
62
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape

123. THE NEURAL NETWORK
62
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
sync

124. THE NEURAL NETWORK
62
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
sense

125. THE NEURAL NETWORK
62
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
percept

126. THE NEURAL NETWORK
62
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
forward
forward

127. THE NEURAL NETWORK
62
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
forward
forward

128. THE NEURAL NETWORK
62
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
forward
forward

129. THE NEURAL NETWORK
62
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
action

130. THE NEURAL NETWORK
62
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
{fitness, halt_flag}

131. THE NEURAL NETWORK
62
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
sync

132. THE NEURAL NETWORK
62
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape

133. THE EXOSELF
63
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
exoself
cortex

134. THE EXOSELF
63
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
exoself
{evaluation_completed, fitness}
cortex

135. THE EXOSELF
63
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
exoself
cortex
fitness > best fitness

136. THE EXOSELF
63
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
exoself
backup_weights
backup_weights
backup_weights
backup_weights
neuron neuron
neuronneuron

137. THE EXOSELF
63
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
exoself
neuron
neuron
perturb_weights
perturb_weights

138. THE EXOSELF
63
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
exoself
cortex

139. THE EXOSELF
63
neuron
neuronneuron
actuatorsensor
neuron
cortex
scape
exoself
cortex
reactivate

140. THE POPULATION MONITOR
64
population monitor
database

141. THE POPULATION MONITOR
64
population monitor
database
private private privateprivate private

142. THE POPULATION MONITOR
64
population monitor
database
private private privateprivate private
start
start start start
start

143. THE POPULATION MONITOR
64
population monitor
database
private private privateprivate private

144. THE POPULATION MONITOR
64
population monitor
database
private private privateprivate private
terminated
terminated terminated
terminated
terminated

145. THE POPULATION MONITOR
64
population monitor
database
private private privateprivate private

146. THE POPULATION MONITOR
64
population monitor
database
private privateprivate

147. THE POPULATION MONITOR
64
population monitor
database
private privateprivate private private

148. THE POPULATION MONITOR
64
population monitor
database
private privateprivate private private
start
start start start
start

149. THE DEVIL IS IN THE DETAILS
•recurrent connections
•newer generations get a higher chance for mutation
•neural plasticity
•public scapes and steady state evolution
65

150. POLE BALANCING
66
agent
cart
actions
percepts

151. DEMO
67

152. DEMO
67

153. BENCHMARK RESULTS
68
Method Single-Pole/Incomplete state
information
Double-Pole/Partial
Information W/O Damping
Double-Pole W/Damping
RWG 8557 415209 1232296
SANE 1212 262700 451612
CNE* 724 76906* 87623*
ESP 589 7374 26342
NEAT - - 6929
CMA-ES* - 3521* 6061*
CoSyNE* 127* 1249* 3416*
DXNN not performed 2359 2313
Our System 647 5184 4792

154. THE HANDBOOK
69

155. Feel free to reach out at:
e. jsoeters@thoughtworks.com
t. @JeroenSoeters
THANK YOU

156. DATA SCIENCE AND ENGINEERING
71