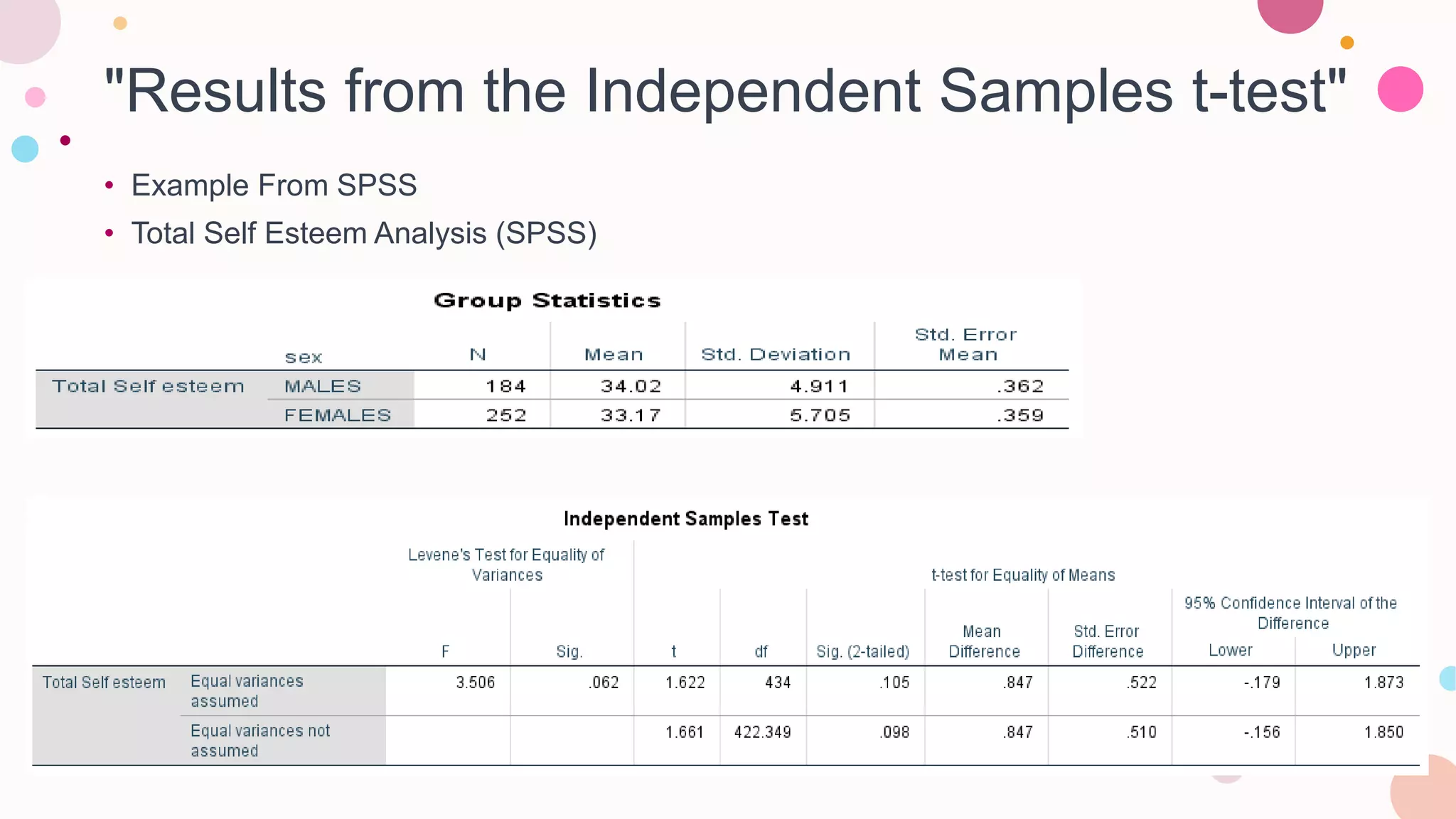
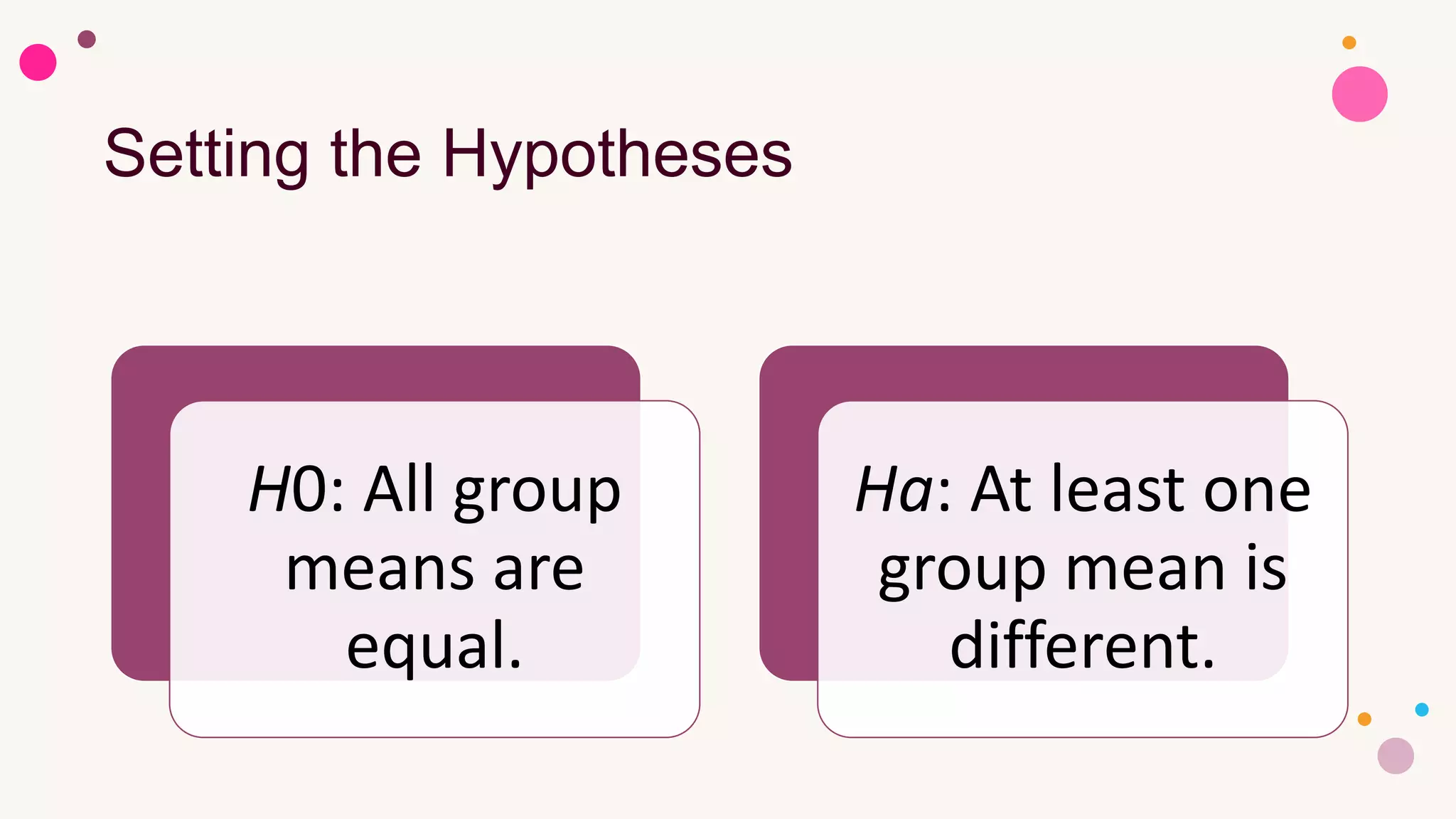
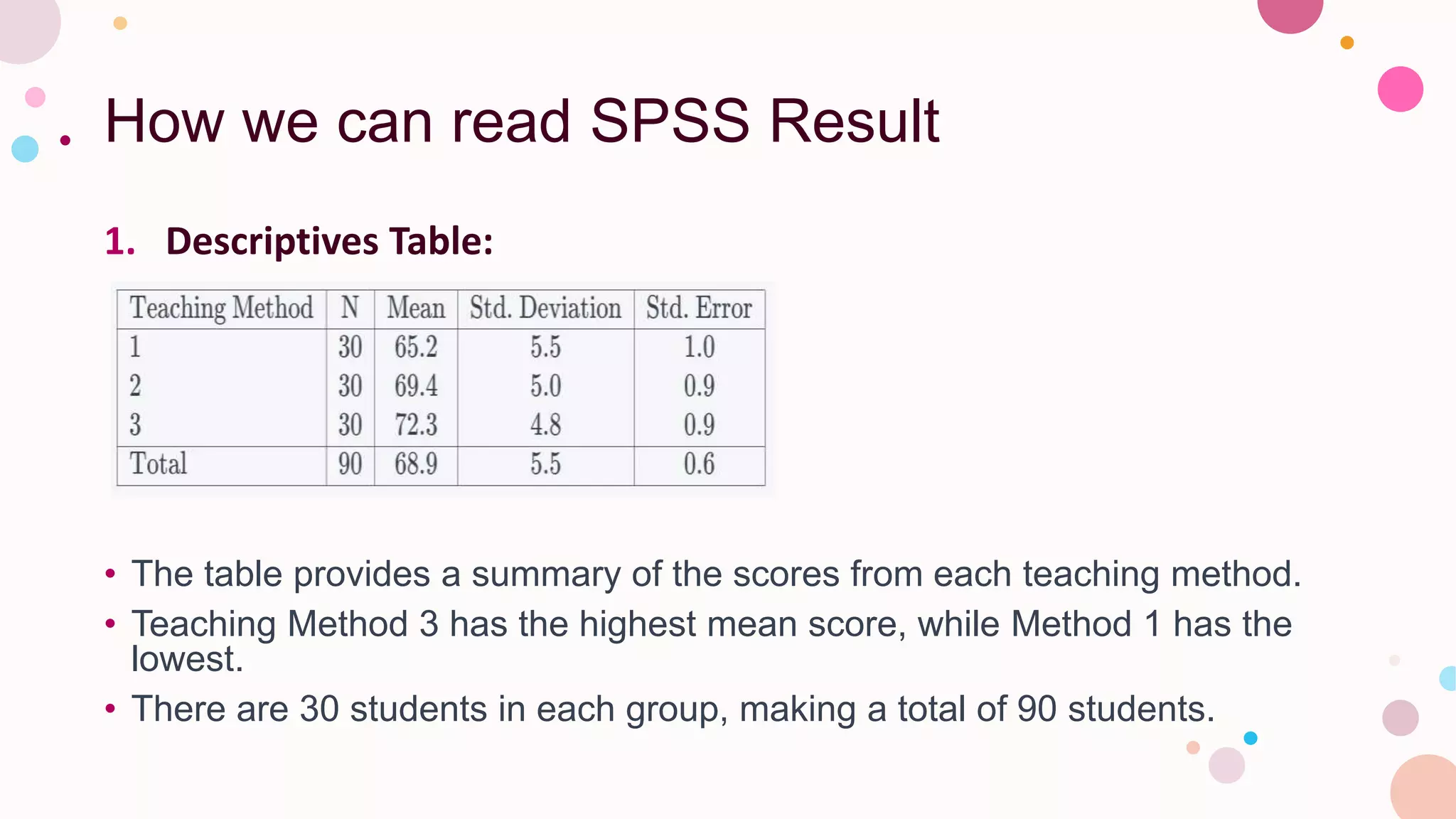
1. The document discusses statistical tests for comparing groups, including the t-test and ANOVA. 2. The t-test is used to compare the means of two groups and ANOVA is an extension for comparing more than two groups. 3. Key assumptions for these tests include normal distribution of data, equal variances between groups, and independent observations. 4. Steps for conducting an ANOVA in SPSS are described, including interpreting the F-statistic to determine if group means are significantly different.

1. Navigating the
Numbers, A Deep Dive
into T-tests & ANOVA
• A Brief Overview
• Presented by: Ahmed Ragab
• August 7, 2023

2. Introduction to
the t-test
• What is the t-test?
• A statistical test used to compare the
means of one or two groups
• Why use the t-test?
• To determine if observed differences are
statistically significant.

3. Types of t-tests:
• One-sample t-test:
• Compares the mean of a single sample to a known value.
• Two-sample (independent) t-test:
• Compares the means of two independent groups.
• Paired-sample t-test:
• Compares the means of the same group under two different conditions.

4. Assumptions of the t-test
• Continuous data(Measured, Not Counted-Decimals and Fractions)
Example (Temperature-time –length/heigh)
Contrast with Discrete Data:(Specific Values, You can't have 3.7 children.& Counted as
apple)
• Data follows a normal distribution(A bell curve or normal distribution graph.)
• Equal variances (for two-sample) &(Homogeneity of Variances), Equal variances mean that
the consistency or spread of data in two groups is alike. If one group has more variation than
the other, they don't have equal variances.
• Independent observations (example)
Independent Observations: Each tree's apple count doesn't affect the other trees. Tree 1 having
5 apples doesn't make Tree 2 have more or fewer apples.
Not Independent: If you measure the height of the same person 10 times in a row, those
measurements are related because they're from the same person.

5. Formula for the t-test

6. "Results from the Independent Samples t-test"
• Example From SPSS
• Total Self Esteem Analysis (SPSS)

7. Levene's Test for Equality of
Variances
Purpose: "Checks if the variances of the two groups are similar."
F-value: "3.506"
p-value (Sig.): "0.062"
Interpretation: "The p-value is greater than 0.05, suggesting that the assumption
of equal variances is met."

8. t-test for Equality of Means
• Equal Variances Assumed:t-value: "1.622"
• Degrees of Freedom (df): "434"
• p-value: "0.105"
• Mean Difference: "0.847"
• 95% Confidence Interval: "-0.179 to 1.873“
• Based on the t-test results, there is no statistically significant difference in self-esteem
scores between males and females. The confidence intervals in both scenarios span from
a negative to a positive range, further affirming the lack of clear difference.

9. Summry
1.Group Differences:
1. Males have a slightly higher mean self-esteem score (34.02) compared to females (33.17).
2.Levene's Test:
1. There's a borderline violation of equality of variances (p = .062).
3.t-test Results:
1. No statistically significant difference in self-esteem between males and females.
2. Assuming equal variances: p = .105; Confidence Interval: (-0.179 to 1.873).
3. Not assuming equal variances: p = .098; Confidence Interval: (-0.156 to 1.850).
4.Conclusion:
1. While there is a slight difference in the mean scores of self-esteem between males and females,
this difference is not statistically significant.
2. fail to reject the null hypothesis (H0).

10. One-Way Analysis of Variance
(ANOVA)
Understanding the Basics

11. What is
One-Way
ANOVA?
Statistical method to test differences
between means.
Used when there are three or more
groups.
Extension of the t-test for multiple
groups.

12. Purpose &
Assumption
s of One-
Way ANOVA
• Determine significant mean differences
between groups.
Purpose:
• Normally distributed dependent
variable.
• Equal population variances.
• Independent observations.
Assumptions:

13. Setting the Hypotheses
H0​: All group
means are
equal.
Ha​: At least one
group mean is
different.

14. How is ANOVA Calculated?
• Compares variance within groups to variance between groups.
• A significant F-statistic suggests group means
differ.

15. Interpreting the Results
Compare F-statistic to critical value. Critical Value=((k−1) and(N−k) degrees of
freedom (where k is the number of groups and N is the total number of
observations).
If F > critical value, reject H0​.
Indicates at least one group differs significantly.

16. Digging Deeper: Post-Hoc
Tests
• If you find a significant difference in a
one-way ANOVA, it only tells you that
at least two groups are different. To
determine which groups are different
from each other, post-hoc tests (like
the Tukey-Kramer procedure) are
used.

17. Conduct a One-Way
ANOVA using SPSS
(Statistical Package
for the Social
Sciences),
• Your dataset should be
structured with one column
representing the dependent
variable (the outcome you're
interested in) and another
column representing the
independent grouping variable
(with categories or groups).
For example:

18. using SPSS
• 1. Start SPSS and Load Your Data:
• Once you've launched SPSS, open your dataset or input the data manually.
• 2. Conducting the One-Way ANOVA:
1.From the main menu, select Analyze.
2.Hover over Compare Means and then select One-Way ANOVA.
3.A new window will pop up. Move your dependent variable (e.g., "Score") into the
"Dependent List" box.
4.Move your independent grouping variable (e.g., "Group") into the "Factor" box.
5.Click on the Options button if you want to request descriptives or homogeneity of variance
test (Levene's test).
6.If you expect that there will be significant differences and you want to know where those
differences lie, click on the Post Hoc button. You can then select a method like "Tukey" to
check pairwise comparisons.
7.Once you've made your selections, click OK.

19. How we can read SPSS Result
1. Descriptives Table:
• The table provides a summary of the scores from each teaching method.
• Teaching Method 3 has the highest mean score, while Method 1 has the
lowest.
• There are 30 students in each group, making a total of 90 students.

20. How we can read SPSS Result
• 2. Test of Homogeneity of Variances (Levene's Test):
The p-value (Sig.) is 0.092, which is greater than the typical alpha level of 0.05.
This means that the assumption of homogeneity of variances is met, and we can
proceed with ANOVA.

21. How we can read SPSS Result
• 3. ANOVA Table:
• The p-value (Sig.) is 0.002, which is less than 0.05. This indicates that there is a
significant difference between the teaching methods.
• The F-statistic (6.82) is the ratio of the variance between the groups to the variance
within the groups.

22. How we can read SPSS Result
• 4. Post Hoc Tests (Tukey HSD):
• The pairwise comparisons indicate that all three teaching methods differ from each other.
• The largest mean difference is between Methods 1 and 3, which is statistically significant
with a p-value of 0.000.
•
Overall Interpretation:
• There are statistically significant differences in scores among the three teaching methods.
Post hoc tests show that each method differs from the others, with Method 3 producing the
highest scores and Method 1 the lowest.