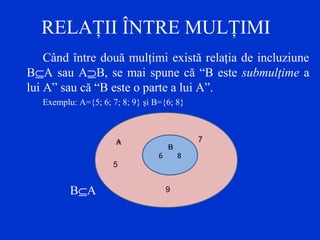
Documentul explică conceptele de mulțimi în matematică, incluzând definiții, reprezentări și relații între mulțimi. Se discută despre operațiile cu mulțimi precum intersecția, reuniunea și diferența, oferind exemple specifice. De asemenea, se subliniază noțiuni importante precum cardinalul unei mulțimi și conceptul de mulțimea vidă.

1. MUL IMIȚClasa a V-a

2. MUL IMI. ELEMENTEȚ
Prin mulțime, în viața de zi cu zi,
înțelegem o grupare, o grămadă, colecție,
clasă, ansamblu etc.
Exemple:
- mul imea elevilor din această clasă;ț
- mul imea ora elor din ROMÂNIA;ț ș
Mul imile se notează cu litere mari dinț
alfabet: A, B, ….

3. MUL IMI. ELEMENTEȚ
N={0, 1, 2, 3, …….} se numeşte
mulţimea numerelor naturale.
N*={1, 2, 3, …….} se numeşte
mulţimea numerelor naturale nenule.

4. MUL IMI. ELEMENTEȚ
Obiectele ce alcătuiesc o mul ime seț
numesc elemente.
Dacă între un element al unei
mulţimi şi mulţimea însăşi scriem
semnul ∈, se spune că am scris relaţia
de apartenenţă a acelui element la acea
mulţime.
De exemplu: a ∈ A (elementul a aparţine
mulţimii A) sau a ∉ A (elementul a nu aparţine
mulţimii A).

5. REPREZENTAREA
MULŢIMILOR
1. Prin enumerarea elementelor
Exemple: 1. A=mulţimea cifrelor impare
A={1; 3; 5; 7; 9}
2. B=mulţimea literelor ce alcătuies cuvântul
matematică
B={m; a; t; e; i; c; ă}
2. Prin proprietăţile caracteristice
Exemple: 1. A={x/x∈N şi x<6}={0; 1; 2; 3; 4; 5}
2. B={x/x∈N, x=3k; k∈N, x≤15}=
={0; 3; 6; 9; 12; 15}

6. 3. Prin reprezentare grafică (diagrame Venn-Euler)
Exemple: 1. A={x/x∈N şi x≤8}
2. B={x/x∈N, x=3k; k∈N, x≤9}
REPREZENTAREA
MULŢIMILOR
2 6
40 8
0
3
6
9

7. Cardinalul unei mulţimi finite
Numărul de elemente al unei mulţimi finite
A se numeşte cardinalul lui A şi se notează cu
card A.
Exemplu: A={1; 2; 3; 4; 5; 7; 9}
card A= 7

8. MULŢIMEA VIDĂ
Mulţimea care nu are nici un element se
numeşte mulţimea vidă şi se notează cu
simbolul Ø.
Ø

9. RELAŢII ÎNTRE MULŢIMI
Când între două mulţimi există relaţia de incluziune
B⊆A sau A⊇B, se mai spune că “B este submulţime a
lui A” sau că “B este o parte a lui A”.
Exemplu: A={5; 6; 7; 8; 9} şi B={6; 8}
B⊆A
6 8
B
A
5
7
9

10. RELAŢII ÎNTRE MULŢIMI
Când între două mulţimi există relaţia de
incluziune strictă B⊂A sau A⊃B se mai spune
că “B este o submulţime proprie a lui A” sau
că “B este o parte proprie a lui A”.
Exemplu: A={5; 6; 7; 8; 9} şi B={x/x∈N şi 5≤x≤9}
B⊂A
5 9 7
8 6

11. RELAŢII ÎNTRE MULŢIMI
 Orice mulţime este inclusă în ea însăşi, A⊆A.
 Mulţimea vidă este considerată o submulţime
proprie a oricărei mulţimi nevide, Ø⊆A.
 Mulţimea formată din toate părţile unei mulţimi
A se numeşte mulţimea părţilor lui A şi se notează
P (A).
 Două mulţimi sunt egale dacă au aceleaşi
elemente, A=B.
 Două mulţimi egale au acelaşi cardinal.
Două mulţimi A şi B sunt egale dacă şi numai
dacă avem simultan B⊆A şi A⊇B.

12. OPERAŢII CU MULŢIMI
INTERSECŢIA
Intersecţia a două mulţimi A şi B este o mulţime
formată din toate elementele comune celor două
mulţimi.
Se notează A∩B şi se citeşte “A intersectat cu B”
A∩B = {x / x ∈ A şi x ∈ B}
Intersecţia este comutativă, A∩B=B∩A.
A B
A∩B
Exemplu: A={1,2, 5, 7, 9} B={1, 5, 9, 10, 15}
A∩B={1, 5, 9}

13. OPERAŢII CU MULŢIMI
REUNIUNEA
Reuniunea a două mulţimi A şi B este o mulţime
formată din elementele care aparţin cel puţin uneia din
cele două mulţimi.
Se notează A∪B şi se citeşte “A reunit cu B”
A ∪ B = {x / x ∈ A sau x ∈ B}
Reuniunea este comutativă, A∪B=B∪A.
A B
A ∪ B
Exemplu: A={1, 3, 5, 7} B={0, 4, 8, 12}
A ∪ B={0, 1, 3, 4, 5, 7, 8, 12}

14. OPERAŢII CU MULŢIMI
DIFERENŢA
Diferenţa a două mulţimi A şi B este o mulţime formată
din elementele care aparţin mulţimii A şi nu aparţin
mulţimii B.
Se notează AB şi se citeşte “A minus cu B”
A B = {x / x ∈ A şi x ∉ B}
Diferenţa nu este comutativă, AB≠BA.
A B
A B
Exemplu: A={1, 2, 5, 7, 9} B={1, 5, 9, 10, 15}
A B={2, 7}

15. AFLAREA ELEMENTELOR A
DOUĂ MULŢIMI PORNIND
DE LA CONDIŢII DATE
Să se afle mulţimile A şi B ştiind că sunt îndeplinite
simultan condiţiile:
a)A∪B={1, 2, 3, 4, 5, 6, 7}
b)A∩B={2, 6, 7}
c)AB={1, 4}
R: A={1, 2, 4, 6, 7}
B={2, 3, 5, 6, 7}