Breviar teoretic

MATEMATICĂ

EVALUAREA NAŢIONALĂ
2011
BREVIAR TEORETIC

CLASA a VIII-a

Material realizat de prof. MACOVEI CRISTINA
Localitatea Bicaz, judeţul Neamt

1

CUPRINS

Pagina
ARITMETICĂ ŞI ALGEBRĂ
Mulţimi……………………………………………………………………………… 3
Calcul algebric………………………………………………………………………. 12
Funcţii……………………………………………………………………………….. 14
Ecuaţii, inecuaţii şi sisteme de ecuaţii……………………………………………… 15
GEOMETRIE
Măsurare şi măsuri………………………………………………………………….. 18
Figuri şi corpuri geometrice…………………………………………………………. 19
Triunghiul……………………………………………………………………………. 22
Patrulaterul convex………………………………………………………………..… 25
Cercul………………………………………………………………………………... 26
Corpuri geometrice………………………………………………………………….. 28

2

ARITMETICĂ ŞI ALGEBRĂ

MULŢIMI
TITLUL EXEMPLE, EXPLICAŢII
CONŢINUTULUI
1 Relaţii între mulţimi Dacă avem: A =1;2;3;4;5}, B = 2;3;5}, C = 3;2;5}.
{ { {

 Apartenenţă, ∈: 2∈A;
 Egalitate, = : B = C;
 Incluziune, ⊂: B⊂A
2 Submulţime Dacă avem: A = 1;2;3;4;5}, B = 2;3;5}.
{ {

 Mulţimea B este o submulţime a mulţimii A pentru că fiecare
element din B aparţine mulţimii A.
3 Operaţii cu mulţimi Dacă avem: A = 1;2;3;4}, B = 2;3;5}.
{ {

 Reuniunea: A∪ = x x ∈
B { A sau x∈ }
B ; A ∪ = 1;2;3;4;5}
B {
.
 Intersecţia: A∩ = x x ∈
B { A si x∈ }
B ; A ∩ = 2;3}
B { .
 Diferenţa: A −B = x x ∈
{ A si x∉ }
B ; A − = 1;4}
B {
.
Produsul cartezian: AΧ ={( x, y ) x ∈A si y ∈ } .
B B

4 Mulţimi finite şi mulţimi  Mulţime finită este mulţimea cu un număr finit de
infinite elemente.
Exemple de mulţimi finite: A = 1;2;3;4}, B = 2;3;5}.
{ {

 Mulţime infinită este mulţimea cu un număr infinit de
elemente.
Exemplu de mulţime infinită: N = 0;1;2;3;...;99,100,....}.
{

5 Mulţimile N, Z, Q, R, RQ  N = 0;1;2;3;...;99,100,....}.
{

 Z ={.... − ;−;−;0;1 2;3;...}.
3 2 1 ;

a  .
 Q =  a ∈Z , b ∈Z *, ( a , b) = 1
 b 


R
este mulţimea numerelor reale ce cuprinde toate
categoriile de numere inclusiv cele scrise sub formă de
radicali.
 {
R − Q = a a nu este patrat perfect à numere }
iraţionale.
6 Relaţia N⊂Z⊂Q⊂R N ⊂ ⊂ ⊂
Z Q R

 Orice număr natural este număr întreg;
 Orice număr întreg este şi un număr raţional;
 Orice număr raţional este număr real.
+2
Exemplu: 2 = +2 =
1
= 4.

7 Scrierea numerelor naturale De exemplu, un număr natural format din trei cifre se scrie în baza
în baza zece zece astfel: abc = a + b +
100 10 c

8 Propoziţii adevărate şi Exemple de propoziţii:
propoziţii false  Propoziţie adevărată: ,, ” 12 : 3 + =
3 7

 Propoziţie falsă: ,, ” 12 : 3 + =
3 2

Prin negarea unei propoziţii adevărate se obţine o propoziţie falsă,
şi invers.
9 Împărţirea cu rest a Dacă avem: 17 : 5 =3 si rest 2.
numerelor naturale Teorema împărţirii cu rest: d =î ⋅c +r, r <î .
17 = ⋅ +
5 3 2

3

TITLUL CONŢINUTULUI EXEMPLE, EXPLICAŢII
1 Divizibilitatea în N  Un număr natural este divizibil cu un alt număr natural dacă
0 restul împărţirii dintre cele două numere este egal cu zero.
 Dacă avem md sau d m atunci: m este multiplul lui d şi d
este divizorul lui m.
 Exemplu: D ={1;2;3;4;6;12} .
12

 Exemplu: M ={0;3;6;9;....;3n;....} .
3

1 Proprietăţile divizibilităţii  Dacă avem md atunci şi (k ⋅m) d .
1 (cele mai uzuale)  Dacă avem md şi nd atunci şi (m ±n)d .
 Dacă avem md şi me iar (d , e) =1 , atunci şi m(d ⋅e) .
1 Criteriile de divizibilitate  a...bc  2 dacă c = 0, sau 2, sau 4, sau 6, sau 8.
2  a...bc 5 dacă c = 0, sau 5.
 a...bc 10 dacă c = 0.
 a...bc  3 dacă a+…+b+c se împarte exact la 3.
 a...bc 9 dacă a+…+b+c se împarte exact la 9.
 dacă bc4 .
a...bc  4

1 Numere prime şi numere  Numere prime sunt numere care au doar doi divizori: pe 1 şi pe
3 compuse el însuşi. Exemple: 2, 3, 5, 7, 11, etc.
 Numere compuse sunt numere care au cel puţin trei divizori.
Exemple: 6, , 12, 15, etc.
1 Numere pare şi numere  Numere pare sunt numere divizibile cu 2. Forma de scriere a
4 impare cestora este 2k , k ∈N .
 Numere impare sunt numere nedivizibile cu 2. Forma de scriere
a cestora este 2k + sau 2k −, k ∈ .
1 1 N

1 Numere prime între ele  Numere prime între ele sunt numere care au ca divizor comun
5 doar numărul 1. Exemple: 4 şi 9; 15 şi 19.
1 Descompunerea unui număr Prin descompunerea unui număr natural într-un produs de puteri de
6 natural într-un produs de numere prime se înţelege scrierea acestuia sub formă de produs de
puteri de numere prime factori care la rândul lor nu se mai pot descompune.
Exemplu: 48 =16 ⋅3 =2 ⋅3. 4

1 C.m.m.d.c. şi c.m.m.m.c. Pentru a afla c.m.m.d.c. şi c.m.m.m.c. se procedează astfel:
7  Se descompun în produs de puteri de numere prime numerele
date:
48 = 2 4 ⋅ 3
180 = 2 2 ⋅ 32 ⋅ 5

 Pentru a afla c.m.m.d.c. se iau factorii comuni (o singură
dată) cu puterea cea mai mică şi se înmulţesc între ei:
( 48,180) =2 ⋅3 =12 . 2

 Pentru a afla c.m.m.m.c. se iau factorii comuni şi necomuni
(o singură dată) cu puterea cea mai mare şi se înmulţesc între
ei:
[ 48,180] =2 ⋅3 ⋅5 =240 .4 2

1 Divizibilitatea în Z Divizibilitatea în Z este asemănătoare cu divizibilitatea în N.
8 În Z: D = −;−;−;+;+;+} .
{ 4 2 1 1 2 4
4

4

TITLUL
CONŢINUTULUI EXEMPLE, EXPLICAŢII
1 Fracţii subunitare, a
9 echiunitare, supraunitare  Fracţii subunitare b
, a < b.

a
 Fracţii echiunitare b
, a = b.

a
 Fracţii supraunitare b
, a > b.

2 Amplificarea şi m)
a a ⋅m
0 simplificarea fractiilor  Amplificarea =
b b⋅m
, m ≠ 0.

(m
a a:m
 Simplificarea b
=
b:m
, m ≠ 0.

2 Fracţii ireductibile  Fracţie ireductibilă este fracţia în care numărătorul şi numitorul
1 sunt numere prime între ele. Exemplu de obţinere a unei fracţii
ireductibile, pas cu pas:
(2 (2 (3
48 24 12 4
= = = .
36 18 9 3

2 Transformări de fracţii abc
2  Fracţii zecimale finite a, bc =
100
.

abc − a
 Fracţii zecimale periodice simple a, ( bc ) =
99
.

abcd − ab
 Fracţii zecimale periodice mixte a, b( cd ) =
990
.
 Exemple:
225 9 13 −1 12 4 213 −21 192 32
2,25 = = . 1, ( 3) = = = . 2,1( 3) = = =
100 4 9 9 3 90 90 15

 O fracţie ordinară se poate transforma într-o fracţie zecimală prin
împărţirea numărătorului la numitorul fracţiei. Exemplu:
22
= 22 : 3 = 7, ( 3).
3

2 Compararea, ordonarea şi  Compararea numerelor raţionale
3 reprezentarea pe axă a 7 6
numerelor reale Dintre numerele a=
6
şi b=
5
mai mare este numărul ….
5) 6)
7 35 6 36
Aducem numerele date la acelaşi numitor: a= =
6 30
şi b= =
5 30
.
Se observă că numărul mai mare este numărul b. Se poate să aducem
numerele date şi la acelaşi numărător iar atunci comparăm numitorii.
 Compararea numerelor reale din care cel puţin unul este număr
iraţional
Dintre numerele a = 3 7 şi mai mare ete numărul ….
b =8

Introducem factorii sub radical şi obţinem: a =3 7 = 63 şi
b =8 = 64 . Se observă că numărul mai mare este numărul b.

5

TITLUL
EXEMPLE, EXPLICAŢII
CONŢINUTULUI 4
2 Valoarea absolută a unui  a, a > 0
4 număr real 
a =  0, a = 0
 Valoarea absolută a unui număr real:
 − a, a < 0

 Valoarea absolută a unui număr iraţional
Dacă avem: a − b , cel puţin unul este iraţional, a <b
, atunci
a −b = b −a . Exemplu: 3 − 2 = 2 − 3.

2 Opusul şi inversul unui  Opusul unui număr real: opusul lui a este −a.
5 număr real 1
 Inversul unui număr real: inversul lui a este .
a
2 Partea întreagă şi partea  Partea întreagă şi partea fracţionară a unui număr real pozitiv:
6 fracţionară a unui număr
real
4,4 este între 4 şi 5.
Partea întreagă [4,4] = 4.
Partea fracţionară {4,4} = 4,4 − [4,4] = 4,4 − 4 = 0,4.
 Partea întreagă şi partea fracţionară a unui număr real negativ:

−2,6 este între −3 şi −2.
Partea întreagă [−2,6] = −3.
Partea fracţionară {−2,6} = −2,6 − [−2,6] = −2,6 +3 = 0,4.
2 Rotunjirea şi aproximarea  Metoda de a aproxima un număr real, mai ales când acesta este o
7 unui număr real fracţie zecimală sau un număr iraţional este folosită la estimări şi
exerciţii de comparare.
 Exemplu: 20 =4,4721359.....

Dacă s-ar cere aproximarea cu două zecimale prin lipsă
atunci am avea: 20 = 4,47 .

Dacă s-ar cere aproximarea cu două zecimale cu adaos atunci
am avea: 20 = 4,48 .

2 Intervale în R;  Interval mărginit închis la ambele margini: [a;b]
8 reprezentarea pe axă

 Interval mărginit închis la una din margini : ( a; b ]

 Interval mărginit deschis la ambele margini: ( a ; b)

 Interval mărginit închis sau deschis la una din margini şi nemărginit
la cealaltă: (−∞; a]

 Interval nemărginit la ambele margini: ( − ;+ ) =R
∞ ∞

6

TITLUL
2 Rădăcina pătrată a unui a =b dacă b 2 = a.

9 număr natural pătrat
perfect
a2 = a dacă a > 0.
În general a2 = a .
Exemplu: 225 = 152 =15 .
3 Algoritmul de extragere a èSă calculăm rădăcina pătrată a lui 55225.
0 rădăcinii pătrate èDespărţim numărul în grupe de câte două cifre, de la dreapta spre stânga.
èNe întrebăm: care este cel mai mare număr al cărui pătrat este mai mic sau egal cu
5.
Acesta este 2; îl scriem în dreapta sus;
èÎl ridicăm la pătrat, obţinem 4 şi-l trecem sub 5, aflăm restul scăderii 1.
èCoborâm grupul de următoarele 2 cifre lângă rest.
èDublăm pe 2 şi rezultatul 4 îl trecem sub 2.
èNe gândim care cifră punem alături de 4 şi rezultatul îl înmulţim cu cifra aleasă
astfel încât numărul dat să se cuprindă în 152.
èNe gândim care cifră punem alături de 4 şi rezultatul îl înmulţim cu cifra aleasă
astfel încât numărul dat să se cuprindă în 152.
èRezultatul fiind 129, îl trecem sub 152 şi aflăm restul scăderii.
Aşadar, radical din 55225 èCifra 3 o trecem la rezultat, alături de 2.
este egal cu 235. èCoborâm următoarea grupă de cifre, pe 25, lângă restul 23.
èCoborâm dublul lui 23, care este 46.
èNe gândim care cifră punem alături de 46, numărul format îl înmulţim cu acea cifră
iar rezultatul să fie mai mic sau egal cu 2325.
èAcesta poate fi 5 şi facem calculele.
èTrecem rezultatul 2325 sub numărul 2325 şi efectuăm scăderea.
èRestul fiind zero, algoritmul s-a terminat, cifra 5 o trecm la rezultat alături de 23.
3 Scrierea unui număr real  Dacă avem 7
atunci acest număr se poate scrie şi 7 = 7 2 = 49 .
1 pozitiv ca radical din
pătratul său 5 5 52 25
 Dacă avem 2
atunci acest număr se poate scrie şi = =
2 22 4

.
3 Reguli de calcul cu  Doi radicali se pot aduna sau scădea numai dacă sunt ,,la fel” adică
2 radicali avem termeni asemenea:
Exemplu: 5+ 4 5− 2 5 = 5 ⋅(1 + − ) = 5 ⋅3 =
4 2 3 5 .
 Înmulţirea radicalilor: a ⋅ b = a ⋅b ; 3 ⋅ 10 = 30 .
Împărţirea radicalilor: a : b = a:b ; 18 : 6 = 3 .
3 Scoaterea şi introducerea  Scoaterea factorilor de sub radical. Prezentăm una din metodele
3 factorilor sub radical cele mai utilizate la scoaterea factorilor de sub radical. Se
descompune numărul dat în produs de puteri de numere prime –
se iau perechi de numere prime egale – dintr-o pereche va ieşi un
factor de sub radical – factorii nepereche vor rămâne sub radical
– factorii ieşiţi sau rămaşi sub radical se înmulţesc.
Exemplu:

216 = 2 3 ⋅33 =2 ⋅3 2 ⋅3 =6 6

 Intro
ducerea factorilor sub radical se bazează pe operaţia
a ⋅ b = a ⋅b . Dacă avem 3 5 pentru a introduce pe 3 sub
radical, se ridică la puterea 2 numărul 3 după care se înmulţeşte
cu 5.
3 5 = 3 ⋅5 = 9 ⋅5 = 45
2
.

7

TITLUL
3 Raţionalizarea numitorilor  Raţionalizarea numitorilor de forma a b .
4 b)
m m⋅ b m b
= = .
a b a b⋅ b ab

6) (3
9 9 6 9 6 9 6 3 6
= = = =
2 6 2 6⋅ 6 2 ⋅6 12 4

 Raţionalizarea numitorilor de forma a b + c . În primul rând
conjugatul numărului a b + c este numărul a b − c . Pentru
raţionalizarea numitorului de această formă, fracţia se va amplifica
cu conjugatul numitorului.
a b −c )
m m ⋅(a b −c) m( a b − c )
= =
a 2b − c 2
.
a b +c (a b + c) ⋅ (a b − c)

4 +2 3 )
5 5 ⋅ (4 + 2 3 ) 20 + 10 3
= = 2 =
4 − 2 3 ( 4 − 2 3 ) ⋅ (4 + 2 3 ) 4 − ( 2 3 ) 2
20 + 10 3 2(10 + 5 3) 10 + 5 3
= = =
16 − 12 4 2
3 Operaţii cu numere reale Adunarea şi scăderea
5 Pentru a efectua adunarea sau scăderea numerelor raţionale este necesar
a parcurge următorii paşi:
 Se transformă fracţiile zecimale în fracţii ordinare;
 Se aduc fracţiile la acelaşi numitor;
 Se efectuează adunarea/scăderea.
Exemplu:
3) 3) 2) (2
3 5 3 8 42 −15 −9 +16 34 17
7 −2,5 − + 2, ( 6) =6 ) 7 − − + = = = .
2 2 2 3 6 6 3
Proprietăţile adunării:
 Adunarea este comutativă: a + b = b + a.
 Adunarea este asociativă: a + b + c = (a + b) + c.
 Elementul neutru al adunării este 0: a + 0 = a.
 Pentru orice a există opusul lui a astfel încât: a + (-a) = 0.
Înmulţirea
 La înmulţirea unui număr întreg cu o fracţie, se înmulţeste numărul
întreg cu numărătorul fracţiei, numitorul rămânănd neschimbat;
 Se transformă fracţiile zecimale în fracţii ordinare;
 La înmulţirea a două fracţii ordinare se înmulţesc
numărătorii între ei şi numitorii între ei.
Exemplu:
(6
7 12 ⋅ 7 84 14
a) 12 ⋅
18
=
18
=
18
=
3
.

( 21
6 14 6 14 ⋅ 6 84
b) 4, (6) ⋅
7
= ⋅ =
3 7 3 ⋅7
=
21
= 4.

Proprietăţile înmulţirii:
 Înmultirea este comutativă: a ⋅ b = b ⋅ a;
 Înmultirea este asociativă: a ⋅ b ⋅ c = (a ⋅ b) ⋅ c;
 Elementul neutru al înmulţirii este 1: a ⋅ 1 = a;
 Înmulţirea este distributivă faţă de adunare sau scădere:
a ⋅ ( b + c ) = a⋅ b + a⋅ c

8

TITLUL
3 Operaţii cu numere reale Împărţirea
5 La împărţirea a două numere raţionale se înmulţeşte primul număr cu al doilea inversat. Exemplu:
( 30
25 5 25 24 25 ⋅ 24 600 20
: = ⋅ = = = .
18 24 18 5 18 ⋅ 5 90 3

Tabelul înmulţirii semnelor: Tabelul împărţirii semnelor:
F1 F2 P D I C
+ + + + + +
+ − − + − −
− + − − + −
− − + − − +
Ridicarea la putere Exemplu:
,,Puterea este o înmulţire repetată” 2 5 = ⋅2 ⋅2 ⋅2 ⋅2 =
2 32

a n =a ⋅ a ⋅ a ⋅... ⋅ a
−2 2
2 3 9
  =  =
3 2 4
1
a− = m
m

a

Operaţii cu puteri:  am ⋅ an = am+n;
a
 1 = 1;  am : an = am-n;
 a1 = a;  (am)n = am⋅n;
 a = 1, dacă a ≠ 0;
0
 (a⋅b)m = am⋅bm.
 0 = 0, dacă a ≠ 0;
a

3 Ordinea efectuării  Într-un exerciţiu de calcul aritmetic ce conţine mai multe operaţii cu
6 operaţiilor şi folosirea numere raţionale se efectuează mai întâi ridicările la putere, apoi
parantezelor înmulţirile şi împărţirile în ordinea în care sunt scrise şi apoi
adunările şi scăderile, la fel, în ordinea în care sunt scrise.
 În exerciţiile de calcul aritmetic care conţin paranteze se efectuează
mai întâi calculele din parantezele mici (rotunde), apoi cele din
paranteze mari (drepte) şi apoi cele din acolade.
 Dacă în faţa unei paranteze ce conţine un număr raţional sau o
sumă/diferenţă de numere raţionale se află simbolul ,,−”, atunci se
poate elimina semnul şi paranteza, scriind numerele din paranteză
cu semnul schimbat.
Exemplu:
{4 +5 ⋅(2 +3 ⋅4 − )] : 17 +3}⋅2 −3 ⋅10 =
[ 2
10 3

= [4 + ⋅(4 + − )] : 17 + }⋅ −
{ 5 12 10 3 8 30 =

= [4 + ⋅6] : 17 + }⋅8 −
{ 5 3 30 =

= [4 + ] : 17 + }⋅8 −
{ 30 3 30 =

={34 : 17 + }⋅8 −
3 30 =

={2 +3}⋅8 −30 =

= ⋅ −
5 8 30 =

=40 −30 =10
.
3 Factorul comun  Dacă f ⋅ a + + + + ) = ⋅ + ⋅ + ⋅ +
( b c .... w f a f b f c ..... + ⋅
f w
atunci
7 şi f ⋅a +f ⋅ + ⋅ +
b f c ..... + ⋅
f w =f ⋅ a + + +
( b c ..... + )
w

 Exemplu: 12 ⋅ + ⋅
3 5 12 − ⋅
12 10 = ⋅ 3 + − ) = ⋅ −) = 24
12 ( 5 10 12 ( 2 −

3 Media aritmetică a1 + a2 + a3 + .... + a n
8  Media aritmetică ma =
n
.

9

TITLUL
3 Media aritmetică  Media aritmetică ponderată
9 ponderată a1 ⋅ p1 + a 2 ⋅ p2 + a3 ⋅ p3 +.... + a n ⋅ pn
mp =
p1 + p2 + p3 +.... + pn

unde pi este ponderea numărului ai .
4 Media geometrică a două  Media geometrică m = a ⋅ b . g

0 numere reale pozitive
4 Raportul a două numere a
1 Dacă avem numerele reale a şi b, atunci raportul lor este egal cu b
.
( 25
a 12,5 1250 50
Exemplu: Fie a =12,5
şi b =3,25
. =
b 3,25
=
325
=
13
.

4 Proprietatea fundamentală a m
2 a proporţiilor Dacă avem proporţia =
b n
atunci a⋅ = ⋅
n b m

4 Derivarea proporţiilor a m
3 Dacă avem proporţia =
b n
atunci mai putem obţine şi proporţiile:

a b b n a ±b m ±n a m
 =
m n
; = ;
a m b
=
n
; =
b±a n ±m
.

a ⋅k m⋅k a m a⋅k m a:k m:k
 = ; = ; = ; =
b n b⋅k n⋅k b⋅k n b n

4 Aflarea unui termen x 7 8 ⋅ 7 56
4 necunoscut dintr-o  Dacă avem proporţia =
8 2
atunci x=
2
=
2
= 28 .
proporţie dată extrem1 mez 2
 În general dacă avem mez1
=
extrem 2
atunci

mez1 ⋅ mez 2 extrem1 ⋅ extrem 2
extrem1 =
extrem 2
şi mez1 =
mez 2
.
4 Mărimi direct  Dacă numerele a, b, c, …., w sunt direct proporţionale cu
5 proporţionale numerele α, β, γ, ...., ω atunci se poate forma un şir de rapoarte
a b c w
egale: = = = .... = =i , unde i este coeficientul de
α β γ ω

proporţionalitate.
 Proprietate generală a unui şir de rapoarte egale:
a b c w a + b + c +.... + w
= = = .... = = .
α β γ ω α + β +γ +.... +ω
 Exemplu de o problemă: Să se împartă numărul 76 în trei părţi
direct proporţionale cu numerele 3, 5, 11. Rezolvare:
a b c a +b +c 76
= = = = = 4 ⇒ a = 3 ⋅ 4 = 12; b = 5 ⋅ 4 = 20;
3 5 11 3 + 5 +11 19
c = 11 ⋅ 4 = 44.
4 Mărimi invers  Dacă numerele a, b, c, …., w sunt invers proporţionale cu
6 proporţionale numerele α, β, γ, ...., ω atunci se poate forma un şir de produse
egale:
a⋅α b ⋅β= ⋅ = = ⋅
= c γ .... w ω

Acest şir de produse egale se poate transforma într-un şir de
rapoarte egale, precum:
a b c w
= = = .... = =i
1 1 1 1 ,unde i este coeficientul de proporţionalitate.
α β γ ω

10

TITLUL
4 Regula de trei simplă  Regula de trei simplă cu directă proporţionalitate
7 2caiete..................... cos tă....................7lei
x caiete..............vor cos ta.............17,5lei
2caiete ⋅17,5lei 35caiete
x= = = 5caiete
7lei 7
 Regula de trei simplă cu inversă proporţionalitate
4muncitori........... fac o lucrare .................... în 14 zile
7muncitori.....vor face aceeasi lucrare ........în x zile
4muncitori ⋅14 zile 56 zile
x= = = 8 zile
7muncitori 7
4 Procente p
8  Procentul este un număr raţional; p% =
100
.

20 1 125 5
 Exemple: 20% = =
100 5
; 125% = =
100 4
.
4 Aflarea a p% dintr-un p
9 număr  Din relaţia p% din a =b
⇒ 100
⋅a = b

30 1800
 Exemplu: 30% din 60 =
100
⋅ 60 =
100
= 18 .
5 Aflarea unui număr când p 100 ⋅ b
0 se cunoaşte p% din el  Din 100
⋅a = b ⇒ a=
p .

100 ⋅ 54
 Exemplu: 45% din x = 54; x=
45
= 120

5 Aflarea raportului p 100 ⋅ b
1 procentual  Din 100
⋅a = b ⇒ p=
a
.
100 ⋅ 20
 Exemplu: x % din 80 = 20; x=
80
= 25.

20 1
Mai explicit: x% = = = 25%
80 4

5 Calculul probabilităţii de nr. de cazuri favorabile
Pr obabilitatea = .
2 realizare a unui eveniment

nr. total de cazuri

 Exemplu. Într-un coşuleţ sunt 8 mere galbene şi 12 mere roşii.
Care este probabilitatea ca luând la întâmplare un măr, acesta să
aibă culoarea roşie?
12 12 3
P=
8 +12
= = = 75%
20 4
.

11

CALCUL ALGEBRIC

TITLUL
1 Calculul cu numere Termenii de forma cl unde c, numit coeficientul termenului,
reprezentate prin litere reprezintă un număr, iar, l, partea literală a termenului, este
formată din numere reprezentate prin litere, eventual, cu diverşi
exponenţi, îi numim termeni asemenea dacă părţile lor literale
sunt identice, iar adunarea lor se numeşte reducerea termenilor
asemenea.
Exemple:
1) Perechi de termeni asemenea: 2 xy si5xy ; −5x y si +4 x y . 2 2 2 3 2 3

2) Adunarea: 3xy + xy + xy − xy =8 xy − xy .
2 5 4 2 2 2 2

3) Înmulţirea: 3x ⋅(−2 xy )⋅(− x y ) =24 x y .
4 2 2 4 3

4) Împărţirea: 28 x y : (7 x y ) =4 xy . 4 5 3 3 2

5) Ridicarea la o putere: (−2 x yz ) =− x y z .
8 2 3 3 6 3 9

6) Ridicarea la o putere cu exponent număr negativ:
−2 +2
 a +b  c +d 
  = 
c +d   a +b 

2 Formulele de calcul Formule utilizate:
prescurtat 1) Produsul dintre un număr şi o sumă/diferenţă: a (b ± ) =
c ab ±ac

2) Pătratul unui binom: (a ±b ) =a ±2ab +b 2 2 2

3) Pătratul unui trinom: (a + + )
b c
2
=a 2 + 2 + 2 + (ab +
b c 2 ac + )
bc

4) Produsul sumei cu diferenţa: (a + )(a − ) =a 2 − 2
b b b

5) Produsul a două paranteze: (a + )(m + ) = (m + ) + (m + )
b n a n b n

Exemple:
1) 2 x ( x +3) =2 x +6 x ; 2

2) (2 x +1)2 =4 x 2 +4 x +1 ;
3) (x 2
+2 x +3) =x 4 +4 x 3 + x 2 + x +9
2
10 12 ;
4) (3x +5)(3x −5) =9 x −25 ; 2

5) (x +2 )(x −5) =x −3x − .10 2

3 Descompunerea în factori Formule utilizate:
1) Scoaterea factorului comun: ab ±ac =a (b ±c )
2) Restrângerea pătratului unui binom: a ±2ab +b 2 2
=(a ±b )
2

3) Diferenţa de pătrate: a −b =(a +b )(a −b ) 2 2

4) Descompunerea unui trinom de forma: x +mx +n ; dacă 2

a ⋅b =n si a + =
b m a, b ∈Z

atunci: x +mx +n =(x +a )(x +b ) .
2

Exemple:
1) 15x −25 x =5 x (3x −5) ;
2

2) 9 x 2 −24 x +16 =(3 x −4 )
2
;
3) 4 x 2 −y 2 = 2 x +y )(2 x −y )
( ;
4) x 2
−x −12 = x + )( x − )
( 3 4 .

12

TITLUL
4 Rapoarte de numere Exemple:
reprezentate prin litere 2x x+ y x2 − 9 2x
3
; 5
; 4
; x− 2
cu condiţia ca numitorul ≠0
.
5 Amplificarea k)
m m⋅k
Amplificarea =
n n⋅k
;
x +2 )
3x 3 x ( x + 2) 3x 2 + 6 x
Exemplu: =
x − 2 ( x − 2)( x + 2)
=
x 2 −4
.

6 Simplificarea m
(k
m:k
Simplificarea n
=
n:k
;
Äpentru a simplifica un raport de fapt se caută c.m.m.d.c. al termenilor
raportului dat.
x2 + 4x + 4
Exemplu: Să se simplifice raportul: x2 − 4
; se descompun în
factori termenii raportului şi după aceea se simplifică.
( x + 2) 2 ( x +2
x2 +4x +4 x +2
= = .
x2 −4 ( x + 2 )( x − 2 ) x −2

7 Adunarea sau scăderea Adunarea sau scăderea
k :n ) k :q )
m p ( k : n ) ⋅ m + ( k : q) ⋅ p
Ä n
+
q
=
k
;

Unde k este c.m.m.m.c. al lui n şi q.
Exemplu:
x −2 )
3x 2 3x 2 3 x 2 −6 x + 2 3 x 2 −6 x + 2
+ 2 = + = = .
x + 2 x −4 x +2 ( x + 2)( x −2) ( x + 2)( x −2) ( x + 2)( x −2)

8 Înmulţirea m p m⋅ p
Înmulţirea ⋅ = ;
n q n⋅q

x x +2 x ( x + 2) x2 +2x
Exemplu: ⋅ =
x + 3 x − 3 ( x + 3)( x − 3)
= 2
x −9
.

9 Împărţirea m p m q m ⋅q
Împărţirea : = ⋅ = ;
n q n p n⋅ p

x −1 2 x −2 x −1 x −2 ( x −1)( x −2) x −2
Exemplu: : = ⋅ = = .
x + 2 x −2 x + 2 2 x −2 ( x + 2) ⋅ 2( x −1) 2 x +4

1 Ridicarea la putere m
a
ma
0 Ridicarea la putere   = a ;
n n
2
 x  x2 x2
Exemplu:   = = 2 .
 x −1  ( x −1) x − 2 x +1
2

1 Ridicarea la putere cu m
−a
na
1 exponent număr negativ Ridicarea la putere  
n
=
ma
;
−2
 x  ( x −1) 2 x 2 − 2 x +1
Exemplu:   = = .
 x −1  x2 x2

13

FUNCŢII

TITLUL
1 Noţiunea de funcţie Daca fiecărui element din mulţimea A îi corespunde un element din


mulţimea B spunem că este definită o funcţie pe A cu valori în B.
 Se notează: f : A →B.
A = domeniul de definiţie,
B = codomeniul funcţiei.
Exemplu: f : { 2;0;1 2;3}→ ,
− ; R f ( x) = +
x 3

2 Funcţii definite pe
mulţimi finite, 7
6

exprimate prin 5
4
diagrame, tabele, 3

formule, grafic 2
1
0
-1 0 2 5

x -1 0 2 3 5 f(x) = x + 2
y 1 2 4 5 7

3 Funcţii de tipul Exemplu:
f:A→R, f(x) = ax + Să se construiască graficul funcţiei
b, unde A este un f:[-2;4)→R, f ( x ) =− x +2 ;
3

interval de numere Pentru x = 2 ⇒( −) = + = ⇒( −;8) ;
− f 2 6 2 8 A 2

reale Pentru x = ⇒( 4) = 12 + = 10 ⇒( 4;− ) ;
4 f − 2 − B 10

Graficul funcţiei este un segment de dreaptă ce uneşte
punctele A şi B, închis în A şi deschis în B.
* Dacă mulţimea A este un interval de numere
mărginit la o extremă şi nemărginit la cealaltă
extremă, atunci graficul funcţiei este o semidreaptă
cu originea în extrema mărginită a intervalului.
4 Functii de tipul Exemplu:
f:R→R, f(x) = ax + Sa se construiască graficul funcţiei f:R→R,
b 12 x 17
f ( x) = −
11 11
;

72 17 55
Pentru x = 6 ⇒ f ( 6) = − =
11 11 11
= 5 ⇒ A( 6;5) ;
Pentru
−60 17 −77
x = − ⇒ f (− ) =
5 5 − = = − ⇒B ( − ;− )
7 5 7
11 11 11

Graficul funcţiei este o dreaptă ce trece prin punctele
A şi B.
ECUAŢII, INECUAŢII, SISTEME DE ECUAŢII

14

TITLUL
1 Ecuaţii de forma Propoziţia cu o variabilă de forma ax + b = 0 se numeşte ecuaţie cu o


ax + =
b 0
, necunoscută, unde a şi b sunt numere reale.
a ∈ *, b ∈ .
R R  Într-o ecuaţie avem ,,dreptul” de a trece termeni dintr-un membru în alt
membru cu semnul schimbat.
 Într-o ecuaţie avem ,,dreptul” de înmulţi/împărţi egalitatea cu un număr
diferit de zero. Procedeul este utilizat pentru eliminarea numitorilor şi
la final aflarea necunoscutei.
Exemplu: 3 x + =x 2 + 2
3

⇒ 3x −x 2 = 2 − 3

⇒ x (3 − 2 ) =−3 − 2 )
(
− (3 − 2 )
⇒ x= = −1 .
3− 2

2 Ecuaţii echivalente  Două ecuaţii sunt echivalente dacă au aceeaşi soluţie.
 Bazându-se pe proprietăţile egalitatăţii, se pot obţine ecuaţii echivalente
pornind de la o ecuaţiei dată.
Exemplu: Fie ecuaţia 2 x −4 =0;
2 x − 4 + 5 = 0 + 5;
a) adunăm la ambii membri ai ecuaţiei numărul 5: 2 x +1 = 5

2x +1 = 5⋅ 3
b) înmulţim ecuaţia (toţi termeni) cu 3: 6 x + 3 = 15

3 Inecuaţii de forma Propoziţia cu o variabilă de forma ax + b > 0 se numeşte inecuaţie cu o
ax + < , ( >≤≥
b 0 , , )
, necunoscutăă, unde a şi b sunt numere reale.
a ∈ *, b ∈ .
R R  Într-o inecuaţie avem ,,dreptul” de a trece termeni dintr-un membru în
alt membru cu semnul schimbat.
 Într-o inecuaţie avem ,,dreptul” de înmulţi/împărţi inegalitatea cu un
număr diferit de zero. Procedeul este utilizat pentru eliminarea
numitorilor şi la final aflarea necunoscutei.
 Dacă o inecuaţie se va înmulţi/împărţi cu un număr negativ atunci
sensul inegalităţi se schimbă.
Exemplu: 5x − < x −
21 8 6
⇒ 8 −
⇒ −3x <15 : ( −3)
5 x −x < 6 +21

⇒ x >−
⇒ x ∈(−5;+ ) .
5 ∞

4 Sisteme de ecuaţii Metoda reducerii:
de forma  Se alege o necunoscută cu scopul de a fi ,,redusă” ţi se identifică
 a1 x + b1 y + c1 = 0 coeficienţii săi;
 ,  Se află c.m.m.m.c. al coeficienţilor şi se înmulţesc ecuaţiile astfel încât să
a2 x + b2 y + c2 = 0
se obţină coeficienţii necunoscutei numere opuse;
a ,a ,b ,b ,c ,c ∈
1 2 1 2 1 2R
 Se adună ecuaţiile şi se obţine o ecuaţie cu o singură necunoscută, după
care se rezolvă;
La fel se procedează şi cu cealaltă necunoscută.
2 x + y = 5 ⋅ 2 4 x + 2 y = 10
Exemplu:  ⇒ 
3x − 2 y = −3 3 x − 2 y = −3
7x =7 ⇒ x =1
;
 2x + y = 5⋅ 3  6 x + 3 y = 15
 ⇒ 
3x − 2 y = −3 ⋅ ( − 2 ) − 6 x + 4 y = 6

x=1
7 y = 21 ⇒ y=3 ⇒  .
y= 3

15

TITLUL
4 Sisteme de ecuaţii Metoda substituţiei:
de forma  Se află dintr-o ecuaţie o necunoscută în funcţie de cealaltă necunoscută;
 a1 x + b1 y + c1 = 0  Se introduce valoarea acestei necunoscute în cealaltă ecuaţie şi se rezolvă
 , ecuaţia;
a2 x + b2 y + c2 = 0
 Se află cealaltă necunoscută.
a1 , a 2 , b1 , b2 , c1 , c2 ∈R
 2x + y = 5
Exemplu:  din 2 x +y =5
⇒ y =5 −2 x
;
3x − 2 y = −3

Introducem pe y =5 −2 x
în 3 x − y =−
2 3
⇒ 3 x − (5 − x ) = 3
2 2 − ⇒
3x − + x = 3
10 4 −
⇒ 7 x =7
⇒ x =1

x=1
Introducem pe x =1
în y =5 −2 x
⇒ y = − ⋅ =3
5 2 1
⇒  .
y= 3

5 Probleme ce se Etapele de rezolvare a unei probleme:
rezolvă cu ajutorul 1. Stabilirea datelor cunoscute şi a celor necunoscute din problemă.
ecuaţiilor, 2. Alegerea necunoscutei (necunoscutelor) şi exprimarea celorlalte date
inecuaţiilor şi a necunoscute în funcţie de aceasta (acestea).
sistemelor de 3. Alcătuirea unei ecuaţii (sistem de ecuaţii) cu necunoscuta
ecuaţii (necunoscutele) aleasă (alese), folosind datele problemei.
4. Rezolvarea ecuaţiei (sistemului de ecuaţii).
5. Verificarea soluţiei.
6. Formularea concluziei problemei.
Exemplul 1(ecuaţie): Un călător parcurge un drum în 3 zile astfel: în prima zi
1 3
parcurge 3
din drum, a doua zi parcurge 5
din rest iar a treia zi ultimii 40
de km. Aflaţi lungimea totală a drumului.
Rezolvare: Stabilim necunoscuta principală – lungimea totală a drumului, pe
care o notăm cu x;
x 2x
În prima zi a parcurs: 3
; i-au rămas de parcurs 3
; a doua zi a parcurs

3 2x 2x
⋅
5 3
=
5
;
5) 3)
x 2x x 2 x 15)
Avem ecuaţia: x= +
3 5
+ 40 pe care o rezolvăm: 15 )
x=
3
+
5
+ 40 ⋅15

⇒ = x +x +
15 x 5 6 600

⇒ −x −x =
15 x 5 6 600 ⇒ =
4x 600 ⇒x =
600
= 150km este lungimea totală
4

a drumului.

Exemplul 2 (inecuaţie): Să se gasească trei numere naturale consecutive a
căror sumă este mai mică decât 16.
Rezolvare: Stabilim necunoscuta principală – numărul cel mai mic pe care îl şi
notăm cu x;
Celelalte două numere vor fi x + 1 şi x + 2
⇒ inecuaţia: x + ++ + <
x 1 x 2
pe care o rezolvăm:
16

13
3x + <
3 16 ⇒ <
3x 13 ⇒ x<
3
⇒ soluţiile: (1;2;3), (2;3;4), (3;4;5), (4;5;6).

TITLUL
EXEMPLE, EXPLICAŢII
16

CONŢINUTULUI
5 Probleme ce se Exemplul 3 (sistem de două ecuaţii): Două creioane şi nouă cărţi costă
rezolvă cu ajutorul împreună 80 de lei. Dacă 5 creioane şi 4 cărţi costă împreună 42 de lei, aflaţi
ecuaţiilor, preţul unui creion şi a unei cărţi.
inecuaţiilor şi a Rezolvare: Stabilim necunoscutele problemei: preţul unui creion = x şi preţul
sistemelor de unei cărţi = y.
ecuaţii 2 x + 9 y = 76
Se formează sistemul de ecuaţii:  pe care îl rezolvăm:
5 x + 4 y = 42

 8 x + 36 y = 304
 2 x + 9 y = 76 ⋅ 4
 ⇒ − 45 x − 36 y = −378

⇒ x = 2 lei (preţul unui creion).
5 x + 4 y = 42 ⋅ ( −9)
− 37 x = −74
Introducem valoarea lui x în prima ecuaţie:
2⋅ + y =
2 9 76 ⇒ =
9y 76 − ⇒ =
4 9y 72 ⇒ =
y 8
lei (preţul unei cărţi).

GEOMETRIE

17

MĂSURARE ŞI MĂSURI
1 Lungime  Unitatea de măsură a lungimii este metrul – m.
 Multiplii metrului - m:
 . 1dam = m
10

 1hm = dam =
10
.
100m

 1km = hm =
10 100dam =1000m
.
 1m = , dam = ,01hm = ,001km
01 0 0
.
 Submultiplii metrului:
 1m = dm =
10 100cm =1000mm
.
 1dm = ,1m = cm =
0 10 100mm
.
 1cm = ,01m = ,1dm = mm
0 0 10
.
 1mm = ,001m = ,01dm = ,1cm
0 0 0
.
2 Arie  Unitatea de măsură a ariei este metrul pătrat – m2.
 Multiplii metrului pătrat – m2:
 1dam = 100m . 2 2

 1hm = 100dam = 10000m2
. 2 2

 1km = 100hm = 10000dam =
2
1000000m 2
. 2 2

 1m = ,01dam = ,0001hm = ,000001km
0 02
0 2
. 2 2

2
 Submultiplii metrului pătrat – m :
 1m = 100dm = 10000cm =
2
1000000mm 2
. 2 2

 1dm = ,01m =
0 100cm =2
10000mm . 2 2 2

 1cm = ,0001m = ,01dm =
0 0 2
100mm . 2 2 2

 1mm = ,000001m = ,0001dm = ,01cm
0 0 2
0 . 2 2 2

 Alte unităţi de măsură a ariei:
 1ha = 10000m . 2

 1ar = 100m ; 1ha = 100ari . 2

3 Volum  Unitatea de măsură a volumului este metrul cub – m3.
 Multiplii metrului cub – m3:
 1dam = 1000m . 3 3

 1hm = 1000dam = 3
1000000m . 3 3

 1km = 10 hm = 10 dam =3
10 m 3
. 3 6 3 9 3

 1m = 10 dam = 10 hm =
3
10 km −3
. 3 −6 3 −9 3

 Submultiplii metrului cub – m3:
 1m = 1000dm = 1000000cm =
3
1000000000mm 3
. 3 3

 1dm = ,001m =
0 1000cm =
3
1000000mm . 3 3 3

 1cm = ,000001m = ,0001dm =
0 03
1000mm . 3 3 3

 1mm = 10 m = 10 dm = 3
10 cm −9
. 3 −6 3 −3 3

 Unitatea de măsură a volumului – litrul .
 1l =1dm . 3

 1m = 1000dm = 1000l3
. 3

 1l =
.
100cl =1000ml

 1dal = l ;
10 1hl = 100l .

4 Unghi  Unitatea de măsură a măsurii unui unghi este – gradul
sexagesimal.
 1 = 60 = 3600 . 0 ' ''

 1 = 60 . ' ''

FIGURI ŞI CORPURI GEOMETRICE
18

CONŢINUTULUI
1 Punctul, dreapta, planul,  Punctul este figura geometrică ce se aseamănă cu o urmă lăsată de un
semiplanul, semidreapta, creion;
segmentul de dreaptă,  Punctul nu are dimensiune;
unghiul  Punctele se notează cu litere mari de tipar: A, B, C,.., A1, A2,…

 Dreapta este figura geometrică ce se aseamănă cu un fir foarte subţire
perfect întins;
 Dreapta are o singură dimensiune - lungimea;
 Dreptele se notează astfel: AB, BC, …, d, d1, d2, …

 Planul este figura geometrică ce se aseamănă cu o pânză foarte subţire
perfect întinsă;
 Planul are două dimensiuni – lungimea şi lăţimea;
 Planele se notează astfel: (ABC) sau α , β , γ , …

 Semiplanul – o dreaptă inclusă într-un plan împarte planul dat în două
semiplane.

 Semidreapta – este dreapta mărginită la un capăt.

 Segmentul de dreaptă – este dreapta mărginită la ambele capete.

 Unghiul – este figura geometrică formată de două semidrepte cu
originea comună.

2 Poziţii relative a două Explicatii:
drepte în spaţiu a) drepte identice;
b) drepte concurente,
d ∩ ={ } ;
1 d 2 O

c) drepte paralele, d ∩d1 2 =∅

şi coplanare;
d) drepte oarecare,
d ∩ =∅ şi necoplanare;
1 d 2

CONŢINUTULUI
19

3 Relaţia de paralelism în e) dacă a || b şi b || c ,
spaţiu atunci şi a || c.

4 Relaţia de perpendicularitate Dacă dreptele a şi b sunt
perpendiculare pe acelaşi plan,
atunci aceste drepte sunt paralele
între ele.
α
a ⊥ ; α
b ⊥ ; a b.

5 Axioma paralelelor Printr-un punct exterior unei drepte se poate duce o singură paralelă la
dreapta dată.
6 Unghiurile cu laturile Explicaţii:
respective paralele Cazul I − unghiurile sunt
congruente;
Cazul II – unghiurile sunt
suplementare.
7 Unghiul a două drepte în Explicaţii:
spaţiu; drepte perpendiculare  Dacă avem dreptele a şi b (necoplanare)
şi este necesar să gasim unghiul dintre
ele, procedăm astfel:
 căutăm o dreaptă paralelă cu una dintre
ele şi care are un punct comun cu
cealaltă
(de ex. b || c);
Unghiul pe care îl formează dreapta c cu
dreapta a este şi unghiul dintre deptele a şi b
( unghiul de măsura ϕ).
8 Dreapta perpendiculară pe Explicaţii:
un plan Dacă dreptele a şi b ⊂ α şi
d ⊥ a si d ⊥ b , atunci şi α
d ⊥ .

Teoremă: O dreaptă perpendiculară pe un
plan este perpendiculară pe orice
dreaptă inclusă în planul dat.
9 Distanţa de la un punct la un Explicaţii:
plan  distanţa de la un punct la un plan este
,,drumul cel mai scurt” de la acel punct
la planul dat;
 distanţa de la un punct la un plan este
lungimea segmentului de dreaptă
perpendicular pe planul dat;
 PQ = distanţa de la punctul P la planul α
dacă PQ⊥α.
PQ ⊥ a , a ⊂ α
Pentru asta este necesar: 
 PQ ⊥ b, b ⊂ α

1 Teorema celor trei b⊂ α
0 perpendiculare a ⊥α 
B∈ b  ⇒ MB ⊥ b
AB ⊥ b 
AB ⊂ α

20

CONŢINUTULUI
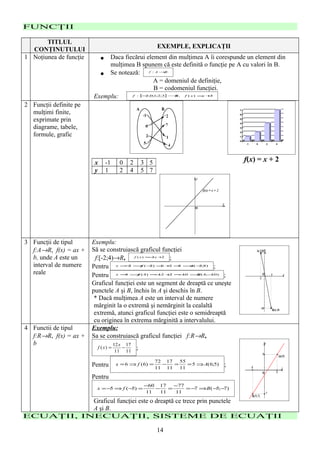
1 Proiecţii de puncte, de Explicatii:
1 segmente de dreaptă şi  Proiecţia unui punct pe un plan este un punct. Dacă AA`⊥α, A` este
de drepte pe un plan proiecţia lui A pe planul α.
 Proiecţia unui segment de dreaptă pe un plan este un segment de dreaptă.
Dacă AA`⊥α, BB`⊥α, A`B` este proiecţia lui AB pe planul α.
 Proiecţia unei drepte pe un plan este o dreaptă. Dacă AA`⊥α, BB`⊥α,
A`B` este proiecţia lui AB pe planul α.
1 Unghiul dintre o Exemplu / aplicaţie:
2 dreaptă şi un plan; Dreapta AB nu este paralelă cu planul α. BC⊥α.
lungimea proiecţiei Unghiul dintre dreapta AB şi planul dat este unghiul
unui segment BAC de măsura β. Dacă BC = 6cm şi AC = 8cm,
BC 6 3
atunci: tgβ = = = .
AC 8 4

1 Unghi diedru; unghiul Explicaţii:
3 plan corespunzător α ∩β = m; b ⊂ β; a ⊂α; a ∩b ={P}
⇒δ = unghiul plan al diedrului
diedrului

1 Plane perpendiculare α ∩ β = a
4 
Explicaţii: Dacă :  b⊂ β ⇒ β ⊥α
 b ⊥α

Sau: Două plane sunt perpendiculare dacă
măsura unghiului plan al diedrului celor două
plane este de 900.
1 Simetria faţă de un  Punctul B este simetricul lui A faţă de
5 punct în plan; simetria punctul O dacă A,O, B sunt coliniare şi
faţă de o dreaptă în AO=OB;
plan  Punctul B este simetricul lui A faţă de
dreapta a dacă A, O, B sunt coliniare, AB⊥a
şi AO=OB.
1 Calculul distanţei de la Exemplu / Fie ABCA`B`C` o prismă triunghiulară regulată dreaptă
6 un punct la o dreaptă aplicaţie: cu muchia bazei de 6 cm şi înălţimea de 8cm. Să se
afle distanţa de la punctul A` la dreapta BC.
Rezolvare: AD⊥BC; AA`⊥(ABC)⇒A`D⊥BC.
l 3 6 3
AD = = = 3 3.
2 2
A`D 2 = AD 2 + AA`2 = 27 + 64 = 91 ⇒ A`D = 91cm.

1 Calculul distanţei de la Exemplu / aplicaţie:
7 un punct la un plan Fie VABC o piramidă triunghiulară regulată dreaptă cu AB = 12 cm şi
înălţimea VO = 2 6 cm. Se cere să se afle distanţa de la punctul O la planul
(VBC).
Rezolvare:
VO ⊥ ( ABC ); OA`⊥ BC ; ⇒VA`⊥ BC
⇒d [O; (VBC )] = d (O;VA`) = OP unde OP ⊥VA`.

l 3 12 3
OA`= = = 2 3; VA`= VO 2 +OA`2 = 24 +12 = 36 = 6.
6 6

VO ⋅ OA` 2 6 ⋅ 2 3 12 2
OP = = = = 2 2 cm.
VA` 6 6

21

CONŢINUTULUI
1 Unghiul dintre două Exemplu / aplicaţie:
8 plane Fie VABCD o piramidă patrulateră regulată dreaptă cu AB = 18cm şi
înălţimea VO = 12 cm. Se cere să se afle sinusul unghiului dintre planele
(ABC) şi (VBC).
Rezolvare:
VO ⊥ ( ABC ); OP ⊥ BC ; ⇒VP ⊥ BC ;
⇒α = este unghiul d int re planele ( ABC ) si (VBC ).

AB 18
OP = = = 9; VP = OP 2 +VO 2 = 81 +144 = 225 = .
15
2 2
(3
VO 12 4
sin α = = = .
VP 15 5

TRIUNGHIUL
CONŢINUTULUI
1 Perimetrul şi aria  Perimetrul P = + +;
a b c

a +b+c
 Semiperimetrul p=
2
;
a ⋅ ha a ⋅ c ⋅ sin B
 Aria A=
2
=
2
= p ( p −a )( p −b)( p −c ) ;

catetă ⋅ catetă
 Aria unui triunghi dreptunghic A=
2
;

l2 3
 Aria unui triunghi echilateral A= .
4

2 Suma măsurilor  Suma măsurilor unghiurilor într-un triunghi este egală cu 180°.
unghiurilor într-un  Într-un triunghi dreptunghic, unghiurile ascuţite sunt complementare.
triunghi
3 Unghi exterior unui  m( ACD) = m( ABC) + m( BAC).
triunghi  m( ACD) = 180° − m( BCA)

4 Linii importante în Mediana Mediatoarea Bisectoarea Înălţimea
triunghi

•Mediana este •Mediatoarea este
•Bisectoarea este •Înălţimea este
segmentul de dreapta
semidreapta ce perpendiculara
dreaptă ce perpendiculară pe
împarte unghiul în dusă din vârful
uneşte vârful mijlocul unei
două unghiuri unui triunghi pe
unui triunghi cu laturi.
adiacente latura opusă.
mijlocul laturii •Punctul de
congruente. •Punctul de
opuse. intersecţie al
•Punctul de intersecţie al
•Punctul de mediatoarelor se
intersecţie al înălţimilor se
intersecţie al numeşte centrul
bisectoarelor se numeşte
medianelor se cercului
numeşte centrul ortocentrul
numeşte centrul circumscris
cercului înscris triunghiului.
22

de greutate. triunghiului. triunghiului.
TRIUNGHIUL

CONŢINUTULUI
5 Linia mijlocie în  Segmentul de dreaptă ce uneşte mijloacele a două
triunghi laturi a unui triunghi se numeşte linia mijlocie.
 MN BC


 BC
 MN = 2

6 Triunghiul isoscel –  Triunghiul isoscel este triunghiul care are două laturi congruente.
proprietăţi [ AB ] ≡[ AC ]

 Într-un triunghi isoscel unghiurile de la bază sunt congruente. ∠≡ C
B ∠

 Într-un triunghi isoscel bisectoarea unghiului de la vârf este şi mediană,
şi înălţime, şi mediatoare.
 Într-un triunghi isoscel medianele (înălţimile sau bisectoarele)
corespunzătoare laturilor congruente, sunt congruente.
7 Triunghiul  Triunghiul echilateral este triunghiul care are toate
echilateral – cele trei laturi congruente. [ AB ] ≡ AC ] ≡ BC ]
[ [
.
proprietăţi  Într-un triunghi echilateral toate unghiurile sunt
congruente şi fiecare are măsura egală cu 60°
A ∠
.
∠≡ B ≡ C
∠

 Într-un triunghi echilaterat bisectoarea oricărui unghi
este şi mediană, şi înălţime, şi mediatoare.
8 Criteriile de Criteriul de congruenţă Criteriul de congruenţă Criteriul de congruenţă
congruenţă a LUL ULU LLL
triunghiurilor

Dacă Dacă  AB = A`B`

 AB = A`B` ∠ABC ≡ ∠A`B`C ` Dacă  BC ≡ B`C `
   AC = A`C `
∠ABC ≡ ∠A`B`C `  BC ≡ B`C ` 
 BC = B`C ` ∠BCA = ∠B`C `A`
  Atunci
Atunci ∆
ABC ≡ A`B `C `
∆
Atunci ∆
ABC ≡ A`B `C `
∆
∆
ABC ≡ A`B `C `
∆

9 Triunghiul Teorema înălţimii AD2 = BD⋅DC
dreptunghic – relaţii Teorema catetei AB2 = BD⋅BC
metrice
Teorema catetei AC2 = DC⋅BC
Teorema lui Pitagora AB2 + AC2 = BC2
10 Relaţii 300 450 600 sin α =
cateta opusă
cos α =
cateta alaturată
;
trigonometrice sin 1 2 3
ipotenuză ipotenuză

2 2 2 cateta opusă cateta alaturată
tgα = ; ctgα =
cateta alaturată cateta opusă
cos 3 2 1
2 sin 2 α cos 2 α=
+ 1
2 2

tg 3 1
3
3

ctg 1 3
3
3

23

CONŢINUTULUI
11 Teorema lui Thales Teorema. O paralelă dusă la o latură într-un triunghi
şi reciproca ei determină pe celelalte două (sau pe prelungirile lor)
segmente proporţionale.
AM AN
=
MB NC
Reciproca. Dacă punctele M şi N determină pe cele
două laturi ale triunghiului ABC segmente
proporţionale atunci MN este paralelă cu BC.
12 Teorema Teorema. O paralelă dusă la o latură într-un triunghi
fundamentală a formează cu celelalte două (sau cu prelungirile lor) un
asemănării triunghi asemenea cu cel dat.
AM MN AN
Ä AB
=
BC
=
AC
.

13 Criteriile de Criteriul de asemănare Criteriul de asemănare LLL Criteriul de asemănare UU
asemănare a LUL Doua triunghiuri sunt asemenea dacă Două triunghiuri sunt asemenea
triunghiurilor Două triunghiuri sunt au toate laturile respectiv dacă au câte două unghiuri
asemenea dacă au câte două proporţionale. respectiv congruente.
laturi respectiv proporţionale
şi unghiurile cuprinse între ele
congruente.

AB BC AC B≡ N; C≡ P
= = .
MN NP MP

AB BC
=
MN NP
; B≡
N

PATRULATERUL CONVEX


24

1 Perimetrul şi aria ARIA UNUI PARALELOGRAM
patrulaterelor studiate ] A =baza ⋅inaltimea =AB ⋅h

] A =AB ⋅AD ⋅sinα

] P = ( AB +
2 AD )

ARIA UNUI DREPTUNGHI
] A =L ⋅l

d 2 ⋅ sin α
] A=
2

] P =2( L +l )
ARIA UNUI PATRAT
] A=l 2

d2
] A=
2
] P =4l

ARIA UNUI ROMB
d1 ⋅ d 2
] A=
2
] A = ⋅h
l

] A =l 2 ⋅sin α

] P =4l

ARIA UNUI TRAPEZ
( B + b) ⋅ h
] A=
2
] P =AB +BC +CD +DA

2 Suma măsurilor unghiurilor Suma măsurilor unghiurilor unui patrulater convex este
unui patrulater convex egală cu 360°.
3 Paralelogramul – proprietăţi Proprietati:
1. Laturile opuse sunt congruente două câte două.
[AB]≡[CD]; [BC]≡[AD] .
2. Unghiurile opuse sunt congruente, A≡ C şi B≡ D;
3. Unghiurile alăturate sunt suplementare, m( A)+m(
B)=1800 şi m( B)+m( C)=1800;
4. Într-un paralelogram diagonalele se intersectează
înjumătăţindu-se, [OA]≡[OC]; [OB]≡[OD] .
4 Dreptunghiul – proprietăţi Alte proprietăţi:
particulare 1. Toate unghiurile sunt congruente şi de 900.
2. Diagonalele sunt congruente.

5 Pătratul – proprietăţi Alte proprietăţi:
particulare 1. Toate laturile sunt congruente;
2. Toate unghiurile sunt congruente şi de 900;
3. Diagonalele sunt congruente;
4. Diagonalele se intersectează perpendicular
una pe cealaltă;
5. Diagonalele sunt şi bisectoarele
unghiurilor.

25

6 Rombul – proprietăţi Alte proprietăţi:
particulare 1. Toate laturile sunt congruente;
2. Diagonalele sunt perpendiculare;
3. Diagonalele sunt şi bisectoarele
unghiurilor.

7 Trapezul – linia mijlocie în Segmentul de dreaptă care uneşte
trapez mijloacele laturilor neparalele se numeşte
linie mijlocie.
B+b
Ä MN =
2 şi MN BC .

B −b
Ä PQ =
2

8 Trapeze particulare Trapez dreptunghic Trapez isoscel

] Într-un trapez isoscel, unghiurile
alăturate bazelor sunt congruente.
] Într-un trapez isoscel diagonalele sunt
congruente.

CERCUL

1 Cercul – centrul rază,  Cercul este locul geometric al tuturor
diametru, disc punctelor dintr-un plan egal depărtate faţă de
un punct fix numit centrul cercului.
 O = centrul cercului;
 OC = raza cercului de lungime R;
 AB = diametrul cercului;
 BD = coardă;
 = arc de cerc;

 = semicerc.
2 Unghi la centru; unghi cu  Unghi cu vârful în centrul cercului
vârful pe cerc
m( AOB) = m( )
 Unghi cu vârful pe cerc
m( BCA) = m( ) / 2.
 Dacă avem două unghiuri congruente
înscrise într-un cerc, cu vârful în centrul
cercului, acestea subîntind între laturile lor,
două arce congruente.

26

3 Coarde şi arce în cerc 1. Dacă arcul AB este congruent cu arcul CD
atunci şi [AB]≡[CD]. Şi reciproca este
adevărată.
2. Dacă MC || ND atunci arcul CD este
congruent cu arcul MN.
3. Dacă OR⊥CD atunci P este mijlocul lui [CD]
şi R este mijlocul arcului CD. O este centrul
cercului; {P}=OR∩CD.
4. Coarde egal depărtate de centru sunt
congruente.
Dacă OP=OQ atunci [CD]≡[AB].
4 Tangenta la cerc dintr-un  Fie punctul P exterior cercului;
punct exterior cercului  PA şi respectiv PB sunt tangente la
cerc;
 OA⊥PA; OB⊥PB;
 [PA] ≡ [PB];
 OP2 = OA2 + AP2
5 Lungimea cercului, aria Lungimea cercului: L =2π = d
R π
discului
Aria discului (cercului): A = πR 2

πR ⋅ α
Lungimea arcului de cerc AC: L AC =
180 0
Aria sectorului de cerc (OAC)
πR 2 ⋅ α
A( OAC ) =
360 0
6 Calculul elementelor în
R 3R 2 3
triunghiul echilateral l =R 3 ; a= ; A= ;
2 4

l2 3
A= ;
4

l 3
h= ; P = 3l .
2
7 Calculul elementelor în pătrat
R 2 l
l =R 2 ; a= = ;
2 2
A = 2R 2 ; A = l2 ;
d =l 2 ; P = 4l .
8 Calculul elementelor în
R 3 3R 2 3
hexagonul regulat l =R ; a= ; A= ;
2 2

3l 2 3
A= ; P = 6l .
2

CORPURI GEOMETRICE
27

CONŢINUTULUI
1 Paralelipipedul Descriere şi desfăşurata corpului Formule:
dreptunghic (la o scară mai mică)
èbaza este un dreptunghi;
èa,b,c =dimensiunile Ab = ab
Al = Pb ⋅ h = 2( ac + bc )
paralelipipedului;
èd = diagonala
paralelipipedului At = 2( ab + bc + ac )
V = abc
D` C`
Baza superioara

B` C` D` A`
A`

d 2 = a 2 + b2 + c 2
A
B C D A
Baza inferioara

D C

2 Cubul Descriere şi desfăşurata corpului Formule:
(la o scară mai mică)
ètoate feţele (6) sunt pătrate;
èl = muchia cubului; Ab = l 2
èd = diagonala cubului;
èare 12 muchii. Al = 4l 2
At = 6l 2
D` C`

A` B` C` D` A`

V = l3
A B C D A

d=l 3
D C

3 Prisma triunghiulară Descriere şi desfăşurata corpului Formule:
èbaza este un triunghi l2 3
echilateral; Ab =
èl = latura bazei; 4
èh = înălţimea prismei Al = Pb ⋅ h = 3l ⋅ h
At = Al + 2 ⋅ Ab
V = Ab ⋅ h

4 Prisma patrulateră Descriere şi desfăşurata corpului Formule:
èbaza este un pătrat; Ab = l 2
èl = latura bazei;
èh = înălţimea prismei; Al = Pb ⋅ h = 4l ⋅ h
èd = diagonala prismei At = Al + 2 ⋅ Ab
V = Ab ⋅ h
d 2 = h 2 + 2l 2

28

CONŢINUTULUI
5 Piramida triunghiulară Descriere şi desfăşurata corpului Formule:
èbaza este un triunghi
echilateral;
èl = latura bazei;
èh = înălţimea piramidei; l2 3
èab = apotema bazei;
Ab =
4
èap = apotema piramidei;
èml = muchia laterală; Pb ⋅ a p
Al =
2 2
a p = h 2 + ab ;
2
èfeţele sunt triunghiuri 2
ml = AO 2 + h 2 isoscele.
2 2 l
2 At = Al + Ab
ml = a p +  
 2 Ab ⋅ h
V=
3

6 Tetraedrul regulat Descriere şi desfăşurata corpului Formule:
 toate feţele l2 3
sunt Ab =
triunghiuri 4
echilaterale
Pb ⋅ a p 3l 2 3
Al = =
; 2 4
 toate At = Al + Ab = l 32

muchiile
Ab ⋅ h l 3 2
sunt V= =
congruente. 3 12
7 Piramida patrulateră Descriere şi desfăşurata corpului Formule:
èbaza este un pătrat;
èl = latura bazei; Ab = l 2
èh = înălţimea piramidei;
èab = apotema bazei; Pb ⋅ a p
èap = apotema piramidei;
Al =
2
èml = muchia laterală;
2 2 èfeţele sunt triunghiuri At = Al + Ab
a p = h 2 + ab ;
isoscele. Ab ⋅ h
2
ml = AO 2 + h 2 V=
2 3
2 2 l
ml = a p + 
 2

29

Breviar teoretic

More Related Content

What's hot

Viewers also liked

Similar to Breviar teoretic

Breviar teoretic