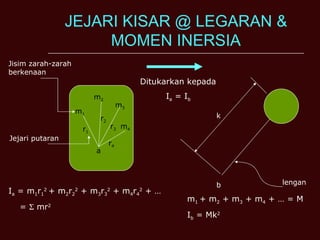
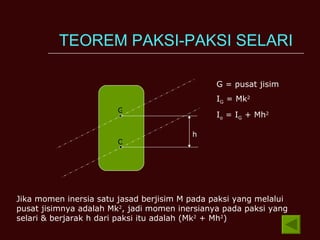
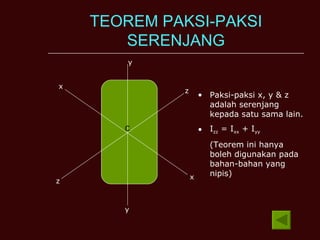
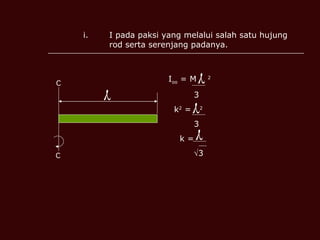
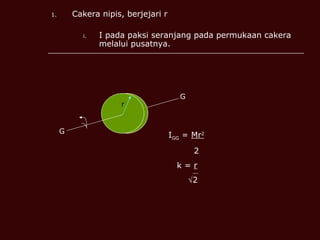
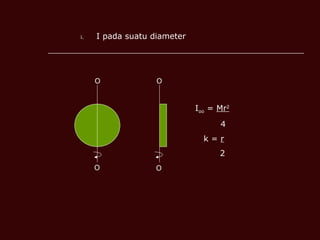
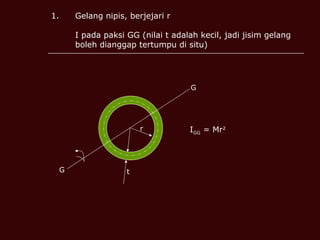
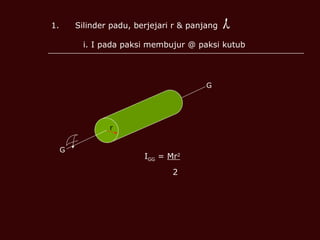
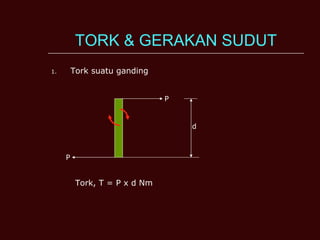
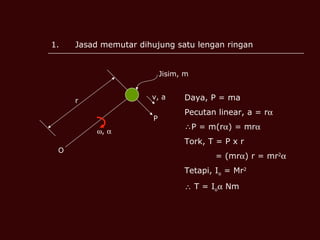
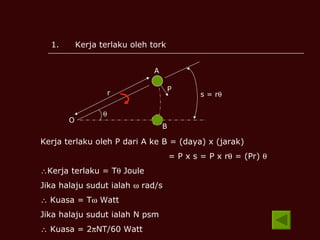
Dokumen tersebut membahas tentang momen inersia, tork, momentum sudut, dan tenaga kinetik yang terkait dengan gerak putar benda. Termasuk definisi momen inersia, teorema paksi selari dan serenjang, serta contoh perhitungan momen inersia, tork, momentum sudut, dan tenaga kinetik untuk berbagai benda seperti silinder, cakera, dan gelang.

1. MOMEN INERSIA JEJARI KISAR @ LEGARAN & MOMEN INERSIA TEOREM PAKSI-PAKSI SELARI TEOREM PAKSI-PAKSI SERENJANG CONTOH-CONTOH NILAI MOMEN INERSIA (I) TORK & GERAKAN SUDUT MOMENTUM SUDUT & IMPULS SUDUT TENAGA KINETIK

2. JEJARI KISAR @ LEGARAN & MOMEN INERSIA m 1 m 2 m 3 m 4 r 4 r 3 r 2 r 1 a b k lengan Ditukarkan kepada I a = I b I a = m 1 r 1 2 + m 2 r 2 2 + m 3 r 3 2 + m 4 r 4 2 + … =  mr 2 m 1 + m 2 + m 3 + m 4 + … = M I b = Mk 2 Jisim zarah-zarah berkenaan Jejari putaran

3. Nilai-nilai m 1 r 1 2 + m 2 r 2 2 + m 3 r 3 2 + m 4 r 4 2 + … ialah momen inersia. Simbol serta unit momen inersia ialah I dan kgm 2 . I a = m 1 r 1 2 + m 2 r 2 2 + m 3 r 3 2 + m 4 r 4 2 + … =  mr 2 Jika jumlah jisim jasad itu adalah M kg & ia tertumpu k meter daripada paksi putaran & diberi bahawa I a = I b serta I b = Mk 2 , k dikenali sebagai jejari kisar @ legaran.  mr 2 = Mk 2 Momen inersia pada paksi membujur bagi satu silinder padu adalah Mr 2 /2 I = Mk 2 = mr 2 /2 dan k = r  2

4. TEOREM PAKSI-PAKSI SELARI G O h G = pusat jisim I G = Mk 2 I o = I G + Mh 2 Jika momen inersia satu jasad berjisim M pada paksi yang melalui pusat jisimnya adalah Mk 2 , jadi momen inersianya pada paksi yang selari & berjarak h dari paksi itu adalah (Mk 2 + Mh 2 )

5. TEOREM PAKSI-PAKSI SERENJANG x x z y z y O Paksi-paksi x, y & z adalah serenjang kepada satu sama lain. I zz = I xx + I yy (Teorem ini hanya boleh digunakan pada bahan-bahan yang nipis)

6. CONTOH-CONTOH NILAI MOMEN INERSIA ( I ) Rod seragam berdiameter kecil, panjangnya I pada paksi ditengah rod serta serenjang padanya   / 2 G G I GG = M 2 12 k 2 = 2 12 k = =  12 2  3    

7. I pada paksi yang melalui salah satu hujung rod serta serenjang padanya. O O  I oo = M 2 3 k 2 = 2 3 k =  3   

8. Cakera nipis, berjejari r I pada paksi seranjang pada permukaan cakera melalui pusatnya. G r G I GG = Mr 2 2 k = r  2

9. I pada suatu diameter O O O O I oo = Mr 2 4 k = r 2

10. Gelang nipis, berjejari r I pada paksi GG (nilai t adalah kecil, jadi jisim gelang boleh dianggap tertumpu di situ) G t r G I GG = Mr 2

11. Silinder padu, berjejari r & panjang i. I pada paksi membujur @ paksi kutub  G G r I GG = Mr 2 2

12. I pada paksi di tengah silinder / 2 G G  I GG = M r 2 + 2 4 12 

13. I pada paksi mengikut diameter yang melalui salah satu hujung silinder O O  I oo = M r 2 + 2 4 3 

14. Silinder geronggang I pada paksi membujur G G r 2 r 1 I GG = I 1 - I 2 = m 1 r 1 2 – m 2 r 2 2 2 2 = ½ m (r 1 2 –r 2 2 ) Dimana: I 1 ,r 1 ,m 1 – silinder padu luar I 2 ,r 2 ,m 2 – silinder padu dalam yang telah dibuang m – jisim selinder geronggang

15. TORK & GERAKAN SUDUT Tork suatu ganding P P d Tork, T = P x d Nm

16. Jasad memutar dihujung satu lengan ringan O  ,  P r v, a Jisim, m Daya, P = ma Pecutan linear, a = r  P = m(r  ) = mr  Tork, T = P x r = (mr  ) r = mr 2  Tetapi, I o = Mr 2  T = I o  Nm

17. Kerja terlaku oleh tork O  r P A B s = r  Kerja terlaku oleh P dari A ke B = (daya) x (jarak) = P x s = P x r  = (Pr)   Kerja terlaku = T  Joule Jika halaju sudut ialah  rad/s  Kuasa = T  Watt Jika halaju sudut ialah N psm  Kuasa = 2  NT/60 Watt

18. MOMENTUM SUDUT & IMPULS SUDUT Momentum sudut Momentum sudut = momen momentum linear pada paksi putaran yang sama. G O  v 2 h r v 1 = r  M kg Momentum linear bagi jasad = Mv 1 = mr  Momen momentum linear pada paksi O = (mr  ) r = mr 2  = I o   Momentum sudut = I o  kgm 2 /s @ Nms

19. Jika pusat graviti di G & jaraknya dari O ialah h, maka I o = I G + Mh 2 (teorem paksi-paksi selari) Momentum sudut pada O = I o  = (I G + Mh 2 )  = I G  + Mh 2  = I G  + Mv 2 h (v 2 = h  ) Prinsip pengabadian momentum sudut : Jumlah momentum sudut dua jasad memutar sebelum hentaman berlaku adalah sama dengan jumlah momentum sudut selepas hentaman berlaku, jika tidak ada tork luar bertindak.

20. Impuls sudut Kadar penukaran momentum sudut suatu jasad ialah secara langsung pada tork luar yang bertindak ke atas jasad itu. Tork, T = I  = I  2 -  1 t T.t = I  2 - I  1 Sebutan “T.t” dikenali sebagai impuls sudut & impuls sudut adalah bersamaan dengan penukaran momentum sudut juga. Unitnya Nms @ kgm 2 /s

21. TENAGA KINETIK Jasad berputar Hitungkan kerja terlaku apabila satu jasad bermomen inersia, I dipecutkan dari kelajuan  1 rad/s hingga  2 rad/s & sudut putarannya  rad.  2 2 =  1 2 + 2  &  =  2 2 -  1 2 2  Tork purata diperlukan, T = I  Kerja terlaku = T  = (I  )  = I  2 2 -  1 2  = ½I  2 2 - ½I  1 2 2 

22. Sebutan “½I  2 ” dikenali sebagai tenaga kinetik putaran  Kerja terlaku = penukaran tenaga kinetik putaran Jasad berguling G G   v v (a) (b) Satu jasad berjisim M, berguling dari (a) ke (b) dengan halaju linear, v & halaju sudut,  Tenaga kinetik translasi = ½Mv 2 Tenaga kinetik putaran pada pusat graviti G = ½I G  2 Jumlah tenaga kinetik jasad berguling = ½Mv 2 + ½I G  2

23. CONTOH 1 Sebuah roda tenaga berjisim 150 kg & berjejari kisar 750 mm dipecutkan dari 20 psm ke 85 psm. Hitungkan peningkatan tenaga kinetik roda tenaga itu.

24. CONTOH 2 Carikan momen inersia serta jejari kisar satu cakera berdiameter 740 mm & tebalnya 60 mm, yang memutar pada paksi membujur. Ketumpatan cakera itu adalah 8000 kg/m 3 . Halaju sudut cakera itu bertambah dari 72 psm ke 220 psm dalam 10 s. Hitungkan nilai tork yang diperlukan untuk putaran terpecut itu.