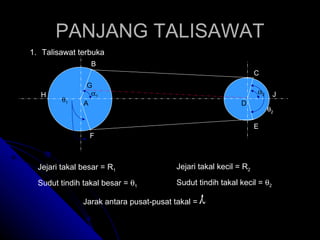
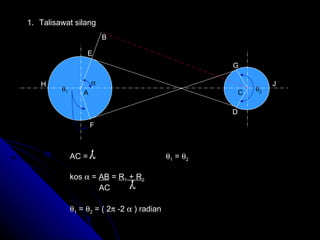
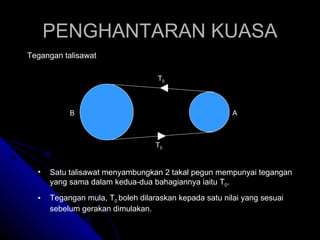
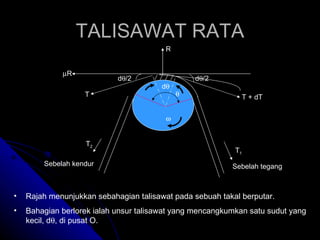
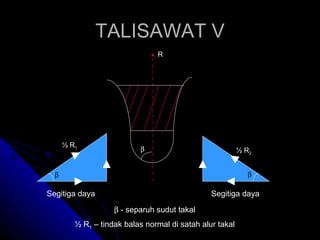
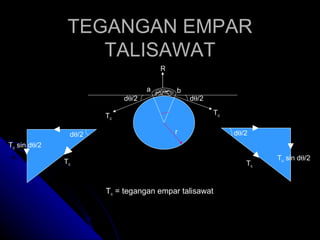
Dokumen tersebut menjelaskan berbagai jenis talisawat yang digunakan untuk menghubungkan dan menghantarkan daya antara dua takal berputar, termasuk talisawat terbuka, silang, rata, V, serta konsep tegangan dan geseran dalam talisawat. Diberikan pula contoh perhitungan untuk menentukan parameter talisawat seperti tegangan, diameter takal, dan kuasa yang dihantarkan.

1. TALISAWAT PANJANG TALISAWAT PENGHANTARAN KUASA TALISAWAT RATA TALISAWAT V TEGANGAN EMPAR TALISAWAT

2. PANJANG TALISAWAT  1  1  2  2 H B C J E D F A G Talisawat terbuka Jejari takal besar = R 1 Sudut tindih takal besar =  1 Jejari takal kecil = R 2 Sudut tindih takal kecil =  2 Jarak antara pusat-pusat takal = 

3. kos  1 = AG = R 1 – R 2 AD  1 =  2 &  2 = 2  2  1 = ( 2  -2  1 ) radian Panjang lengkok BHF = R 1  1 Panjang lengkok CJE = R 2  2 sin  1 = GD  GD = sin  1 AD GD = BC = FE  Panjang talisawat = R 1  1 + R 2  2 + 2 sin  1   

4. Talisawat silang  1   2 H E G J D C F A B AC =  1 =  2 kos  = AB = R 1 + R 2 AC  1 =  2 = ( 2  -2  ) radian  

5. Panjang lengkok EHF = R 1  1 = 2R 1 (  -  ) Panjang lengkok DJG = R 2  2 = 2R 2 (  -  ) sin  = BC  BC = sin  AC BC = ED = FG  Panjang talisawat = R 1  1 + R 2  2 + 2 sin   

6. PENGHANTARAN KUASA Tegangan talisawat T 0 T 0 B A Satu talisawat menyambungkan 2 takal pegun mempunyai tegangan yang sama dalam kedua-dua bahagiannya iaitu T 0 . Tegangan mula, T 0 boleh dilaraskan kepada satu nilai yang sesuai sebelum gerakan dimulakan.

7. T 1 T 2 B A Tegang Kendur Takal terpacu Takal pemacu Oleh kerana ada geseran di antara talisawat & takal. Satu bahagian talisawat itu adalah tegang (tegangan naik dari T 0 ke T 1 ) dan satu bahagian lagi adalah kendur (tegangannya susut dari T 0 ke T 2 ) bila satu tork dikenakan pada takal pacu. Perbezaan tegangan di antara T 1 & T 2 diperlukan untuk penghantaran tork. T 0 = T 1 + T 2 2

8. Kuasa dihantarkan oleh talisawat = (T 1 – T 2 )r x 2  N Watt 60 = (T 1 – T 2 ) x 2  rN Watt 60 = (T 1 – T 2 ) v Watt

9. TALISAWAT RATA R  R T d  /2 d  /2 T + dT T 1 T 2 Sebelah kendur Sebelah tegang   d  Rajah menunjukkan sebahagian talisawat pada sebuah takal berputar. Bahagian berlorek ialah unsur talisawat yang mencangkumkan satu sudut yang kecil, d  , di pusat O.

10. Unsur itu diimbangkan oleh 4 daya seperti berikut: Tegangan (T + dT) disebelah tegang. Tegangan T disebelah kendur. Tindak balas normal, R. Daya geseran,  R yang bersudut tepat kepada R. T 1 = e  T 2 Dimana:  = sudut tindih @ sudut sentuh minimum dalam radian. e = pemalar bernilai 2.718  = pekali geseran di antar talisawat & takal.

11. Untuk pemacu talisawat yang menggunakan saiz-saiz takal yang berlainan, kegelinciran akan berlaku di takal kecil terlebih dahulu sebab ia mempunyai sudut tindih yang lebih kecil. Kuasa = (T 1 – T 2 ) v = T 1 – T 1 v e  = T 1 1 - 1 v Watt e 

12. CONTOH 1 Satu talisawat rata menyambungkan sebuah takal diameter 1.3 m yang memutar dengan 230 psm kepada takal yang lain yang memutar dengan 490 psm & sudut sentuhnya 165  . Jika pekali geseran 0.23 & kuasa 7.5 kW. Hitungkan: i. Tegangan-tegangan talisawat. ii. Tegangan mula talisawat. iii. Diameter takal kedua

13. TALISAWAT V R    ½ R 1 ½ R 2  - separuh sudut takal ½ R 1 – tindak balas normal di satah alur takal Segitiga daya Segitiga daya

14. Dari rajah: Tindak balas takal, R = ½ R 1 sin  + ½ R 1 sin  = R 1 sin  Jumlah daya geseran =  (½ R 1 ) +  (½ R 1 ) =  R 1 =  R =  R sin  sin  Jadi, daya geseran talisawat & takal v bertambah dengan nisbah 1 : 1. sin  2. Maka sebuah takal v adalah setara dengan takal rata yang mempunyai pekali geseran  @  kosek  . sin  Untuk talisawat v, T 1 = e  /sin  = e  kosek  T 2

15. TEGANGAN EMPAR TALISAWAT R b a d  /2 T c r T c d  /2 d  /2 T c sin d  /2 T c T c d  /2 T c sin d  /2 T c = tegangan empar talisawat

16. Dari rajah: ab ialah unsur talisawat & T c tegangan emparnya bila ia memutar. Jika, M = jisim seunit panjang talisawat v = laju talisawat Jisim unsur = M (r d  ) Daya empar unsur = (Mr d  ) x v 2 /r = Mv 2 d 

17. T c = Mv 2 TAKAL RATA T 1 – T c = e  T 2 – T c Kuasa = (T 1 – T c ) 1 - 1 v Watt e  TAKAL V T 1 – T c = e  kosek  T 2 – T c Kuasa = (T 1 – T c ) 1 - 1 v Watt e  kosek 

18. Untuk kuasa maksimum (T 1 adalah tetap) T c = 1/3 T 1 dan v = T 1 laju talisawat sepadan 3M 

19. CONTOH 2 Dua takal berbentuk v disambungkan oleh satu talisawat yang mempunyai sudut kandung 45  . Takal pemacu berdiameter 250 mm, sudut sentuhnya 110  dan ia berputar dengan 750 psm. Jika jisim talisawat adalah 0.372 kg/m dan koefisien geseran di antara talisawat dan takal 0.32, carikan: Tegangan talisawat di kedua-dua belah apabila ia menghantarkan 500 W. Tork yang bertindak pada aci takal pemacu.