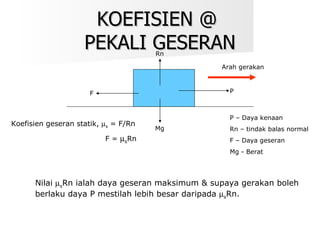
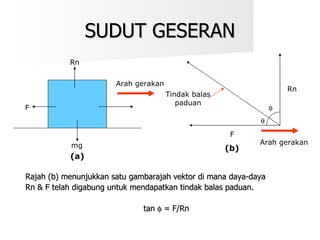
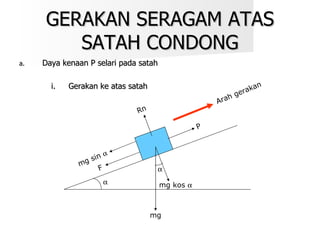
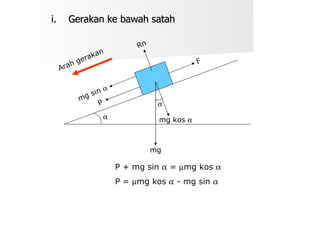
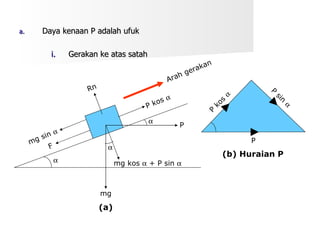
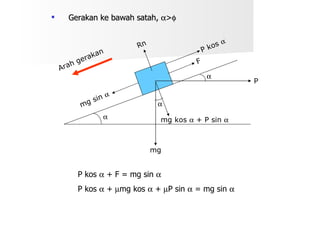
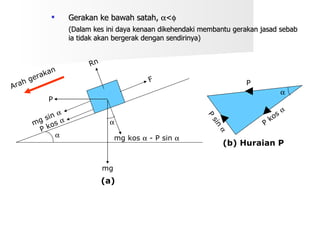
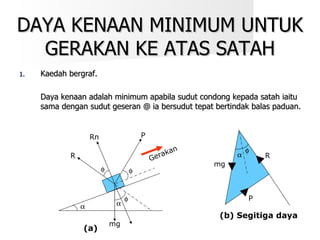
Dokumen ini membahas tentang hukum-hukum geseran, termasuk definisi dan jenis-jenis geseran, serta hubungan antara daya geseran dan tindak balas normal. Terdapat juga beberapa contoh perhitungan koefisien geseran dan sudut geseran untuk berbagai situasi. Selain itu, dokumen ini menjelaskan kecekapan dalam pengendalian daya kenaan dengan dan tanpa geseran.

1. GESERAN PENGENALAN HUKUM-HUKUM GESERAN KOEFISIEN @ PEKALI GESERAN SUDUT GESERAN GERAKAN SERAGAM ATAS SATAH CONDONG DAYA KENAAN MINIMUM UNTUK GERAKAN KE ATAS SATAH KECEKAPAN, 

2. PENGENALAN Geseran boleh ditakrifkan sebagai daya rintangan yang bertindak ke atas suatu badan yang mana daya ini cuba menahan @ melambatkan suatu badan dari mengelunsur @ tergelincir di atas permukaan bersentuhan. Pada umumnya terdapat 2 jenis geseran yang berlaku: Geseran bendalir Geseran kering

3. HUKUM-HUKUM GESERAN Geseran di antara 2 permukaan bergantung pada jenis bahan yang bersentuh. Daya geseran menghad berkadar terus kepada tindak balas normal di antara 2 permukaan & ia adalah bebas dari luas permukaan sentuh. Arah daya geseran selalunya menentang arah gerakan.

4. KOEFISIEN @ PEKALI GESERAN Rn Arah gerakan P Mg F P – Daya kenaan Rn – tindak balas normal F – Daya geseran Mg - Berat Koefisien geseran statik,  s = F/Rn F =  s Rn Nilai  s Rn ialah daya geseran maksimum & supaya gerakan boleh berlaku daya P mestilah lebih besar daripada  s Rn.

5. CONTOH 1 Satu daya 34.3N diperlukan untuk menggerakkan sebuah badan, beratnya 98N, sepanjang satu permukaan datar. Hitungkan koefisien geseran di antara permukaan-permukaan sentuh

6. Rajah di bawah menunjukkan satu jasad, beratnya 98N, ditarik oleh satu daya 32.4N yang bercondongan dengan 20  kepada garis ufuk. Jasad itu diletakkan di atas satu permukaan ufuk & ia bergerak dengan halaju seragam. Carikan pekali geseran di antara jasad & permukaan itu. 20  32.4N 98N Arah gerakan

7. SUDUT GESERAN Rajah (b) menunjukkan satu gambarajah vektor di mana daya-daya Rn & F telah digabung untuk mendapatkan tindak balas paduan. tan  = F/Rn   Arah gerakan Tindak balas paduan Rn F mg Rn F Arah gerakan (a) (b)

8. Nilai  adalah maksimum apabila F ialah maksimum, iaitu F =  Rn tan  =  Rn/Rn =  Dan  dinamakan sudut geseran dalam keadaan ini.

9. CONTOH 2 Sebuah bongkah logam berjisim 3kg ditarik oleh sesuatu daya ufuk 11.77N & ia bergerak dengan halaju seragam di atas satu permukaan datar. Carikan pekali geseran & sudut geseran.

10. CONTOH 3 Sebuah mesin berjisim 430kg ditarik sepanjang satu lantai ufuk oleh satu daya bernilai 1027N yang bercondongan pada 30  kepada garis ufuk. Hitungkan koefisien geseran di antara permukaan itu.

11. GERAKAN SERAGAM ATAS SATAH CONDONG Daya kenaan P selari pada satah Gerakan ke atas satah P mg sin  Rn Arah gerakan   mg kos  mg F

12. Langkah-langkah penyelesaian: Huraikan berat jasad serenjang & selari pada satah. Carikan ungkapan daya geseran, iaitu F =  Rn. Samakan jumlah daya-daya yang bertindak ke atas kepada jumlah daya-daya yang bertindak ke bawah satah. P = mg sin  +  mg kos 

13. Gerakan ke bawah satah F mg sin  Rn Arah gerakan   mg kos  mg P P + mg sin  =  mg kos  P =  mg kos  - mg sin 

14. Perhatikan bahawa: Jasad akan bergerak ke bawah satah tanpa daya kenaan jika  >  . Jasad tengah nak bergerak ke bawah satah, jika  =  & P = 0. Jasad tidak akan bergerak ke bawah satah, jika  <  , melainkan daya kenaan P bertindak padanya.

15. Daya kenaan P adalah ufuk Gerakan ke atas satah P kos  mg sin  Rn Arah gerakan   mg kos  + P sin  mg F P  P kos  P P sin  (b) Huraian P (a)

16. Rn = mg kos  + P sin  F =  Rn =  (mg kos  + P sin  ) P kos  = mg sin  + F = mg sin  +  (mg kos  + P sin  )

17. Gerakan ke bawah satah,  >  F mg sin  Rn Arah gerakan   mg kos  + P sin  mg P kos   P P kos  + F = mg sin  P kos  +  mg kos  +  P sin  = mg sin 

18. Gerakan ke bawah satah,  <  (Dalam kes ini daya kenaan dikehendaki membantu gerakan jasad sebab ia tidak akan bergerak dengan sendirinya) F mg sin  Rn Arah gerakan   mg kos  - P sin  mg P kos  P  P P sin  (b) Huraian P (a) P kos 

19. Rn = mg kos  - P sin  F =  Rn =  (mg kos  - P sin  ) Jumlah daya-daya ke bawah satah = mg sin  + P kos  mg sin  + P kos  =  (mg kos  - P sin  )

20. DAYA KENAAN MINIMUM UNTUK GERAKAN KE ATAS SATAH Kaedah bergraf. Daya kenaan adalah minimum apabila sudut condong kepada satah iaitu sama dengan sudut geseran @ ia bersudut tepat bertindak balas paduan.      mg R P Rn Gerakan (a)   P mg R (b) Segitiga daya

21. Dari segitiga daya: sin (  +  ) = P/mg Nilai minimum, P = mg sin (  +  )

22. Kaedah penghitungan      mg R P Rn 90  -  90  -  Sudut di antara P & R = 90  +  -  = 90  + (  -  ) Sudut di antara mg & R = 180  -  -  = 180  - (  +  ) Nilai minimum P ialah mg sin (  +  ) & sudut condongnya kepada satah ialah sama dengan sudut geseran

23. KECEKAPAN  = Daya guna unggul Daya guna sebenar = Daya kenaan tanpa geseran Daya kenaan dengan geseran

24. Sebuah bongkah logam berjisim 62kg ditahankan dari menggelunsur ke bawah satu satah yang bercondongan pada 35  kepada garis ufuk oleh satu daya 100N. Daya itu bertindak ke atas serta selari dengan satah. Carikan pekali geseran & sudut geseran. Kemudian bongkah itu ditarik ke atas oleh satu daya P yang bertindak pada 15  kepada permukaan satah. Hitungkan: Nilai P Kecekapan pengendalian itu. CONTOH 4